考慮時間影響的樁錨支護深基坑流固耦合分析

周 勇，王 寧，王正振，王延凱

(1. 蘭州理工大學甘肅省土木工程防災減災重點實驗室，蘭州 730050； 2. 蘭州理工大學西部土木工程防災減災教育部工程研究中心，蘭州 730050； 3. 蘭州理工大學土木工程學院，蘭州 730050)

隨著中國經濟建設的迅猛發展，城市人口越來越多，地下空間的開發和使用變得十分必要，由此產生了大量的深基坑工程。在地下水位比較高的地區，深基坑在開挖前往往需要降水，因開挖卸荷以及降水滲流導致的土體應力、強度、變形等特性的改變已經成為影響基坑開挖穩定性的關鍵性因素。然而地下水對支護結構的作用機理的理論研究還遠落后于實踐經驗，目前基坑支護設計方法[1]只是考慮了水土合算還是分算問題，而沒有考慮到基坑開挖和降水是應力場和滲流場共同作用的過程，因此，深基坑降水開挖很有必要考慮流固耦合效應，基于比奧固結理論運用有限元數值計算方法解決流固耦合問題是目前比較有效的方法[2-7]。

朱彥鵬等[8]運用有限元軟件分析了滲流場-應力場耦合作用下的支護結構位移，發現降水與未降水相比，降水工況下基坑總位移大于未降水工況下的總位移。張俏楚等[9]應用三軸試驗對基坑開挖與降水交替作用下土體強度和變形進行模擬分析，發現降水能顯著減小坑內土體回彈。鄭剛等[10]、曾超峰等[11]從基坑開挖前預降水對基坑支護結構變形的影響做了深入研究。劉念武等[12]認為管道沉降和地表沉降的變化趨勢相似，且均呈一定的空間效應，管道沉降和土體沉降的差異主要是由于管道具有一定的抗彎能力所致。楊果林等[13]分析了泥炭土深基坑考慮流固耦合時支護結構變形與內力的特點，發現考慮流固耦合時排樁的最大位移和最大彎矩都發生了顯著變化。

傳統的基坑工程設計是基于瞬態設計的，由于分步降水和逐層開挖是動態性的，所以土體參數也是動態變化的，現分析考慮流固耦合的樁錨支護深基坑變形與支護結構內力隨時間的變化，從而對設計施工提出合理性建議。

1 工程背景

1.1 工程概況

1.2 水文地質條件

場地地下水位于地表以下3m處，需要坑內降水，地下水類型包括孔隙潛水和基巖裂隙水。孔隙潛水主要分布在人工填土層，此層透水性好，屬于強透水層，裂隙水主要存在于全風化及強風化花崗巖中，風化巖層透水性一般，儲水性也較弱。

1.3 基坑支護設計方案

此工程采用樁錨支護，開挖深度為15m，混凝土灌注樁樁徑為1 000mm，樁間距為1500mm，樁長為22m，樁嵌固深度為7m，混凝土強度等級為C30，樁頂設置混凝土強度等級為C25的冠梁，樁體外側掛網噴漿，混凝土面層厚度為100mm，強度等級為C20。預應力錨索采用4排高強鋼絞線，錨索鉆孔孔徑為150mm，具體錨索設計參數如表 1所示，樁錨支護結構剖面圖如圖 1所示。

表 1 錨索的設計參數Table1 Design parameters of anchor cable

表 2 各土層力學參數Table2 Mechanical parameters of each soil layer

表 3 計算工況Table3 Calculation condition

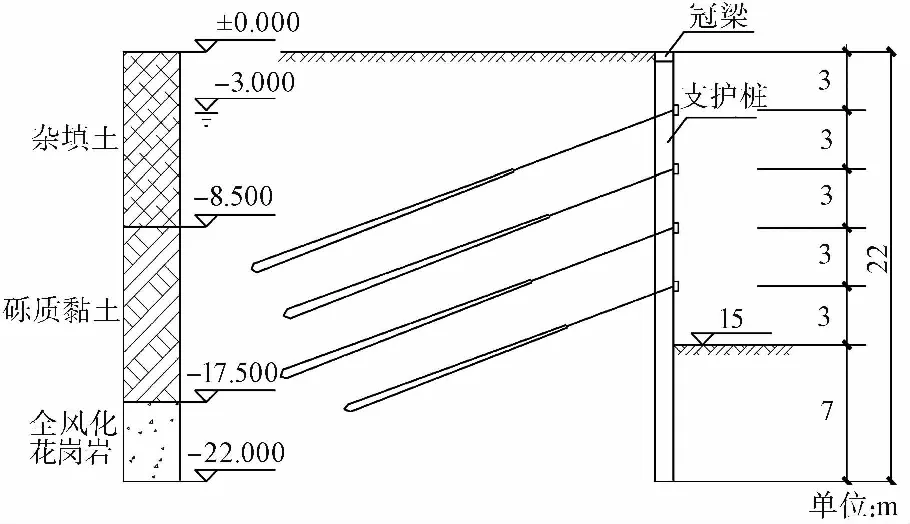
圖 1 樁錨支護結構剖面圖Fig.1 Cross-section of pile-anchor supporting structure

2 數值模擬

2.1 有限元模型建立

采用巖土軟件PLAXIS建立兩個有限元模型。其中，一個模型根據工程實際情況考慮流固耦合，在每個開挖步前設定降水步，通過調節水位實現降水，并進行滲流計算；另外一個不考慮流固耦合，初始水位設定為模型底部。并且兩個模型都在每個開挖步后設定固結期(未考慮流固耦合的模型設定間隔期)，錨索鉆孔及錨索安裝、張拉都需要大概10d的時間保證，而這個過程基坑土體固結變形仍在進行，添加固結期或間隔期(設定為10d)來研究時間因素對深基坑變形與內力計算結果的影響，并對二者變形與內力做出對比分析。

表 2 所示為模型具體的土層參數，表 3所示為考慮流固耦合的基坑降水開挖工況，相比而言，未考慮流固耦合的基坑開挖工況僅僅沒有降水步。

根據工程經驗，此工程問題可簡化為平面應變問題，因此，建立二維有限元模型，模型長度為120m，寬度為60m，模型底面采用固定約束，兩個側面邊界限制水平位移，上表面設定為自由邊界。關于透水性，模型左側設定為透水邊界，右側邊界及底部設為不透水邊界。由于基坑降水開挖是個反復加卸載的過程，土體采用土體硬化(hardening soil，HS)模型，考慮流固耦合的模型計算類型均設置為固結計算，以考慮超靜水壓隨時間的變化與消散，未考慮流固耦合的模型設定為塑性變形計算。排樁采用了板單元模擬；錨桿自由段采用點對點錨桿單元；錨桿錨固段采用土工格柵來模擬；支護結構與土體之間采用界面單元分隔開。為不失一般性，在坑外離基坑邊緣10m處作用長度為10m，大小為15kN/m的均布荷載，有限元模型如圖 2所示。模型建立之后進行單元格劃分，總共劃分了1247個15節點單元，節點數為10507個，應力點數為14964個，有限元模型網格劃分如圖 3所示。

圖 2 有限元計算模型Fig.2 Finite element calculation model

圖 4 考慮流固耦合的樁體水平位移Fig.4 Horizontal displacement of pile considering fluid structure coupling

2.2 數值模擬變形分析2.2.1 樁體水平位移

圖4 為考慮流固耦合時基坑開挖過程的樁體水平位移曲線。可知，隨著開挖深度增加，樁體水平位移不斷增大，位移最大值位置也逐漸下移，最終在樁體中部水平位移達到最大，曲線呈現出“魚腹”狀。其中，當開挖深度為3、6、9、12、15m時，樁體水平位移最大值依次為-2.93、5.95、11.68、21.25、36.24mm，需要說明的是開挖一樁體上部負位移的產生是由于開挖后錨索預應力的及時施加導致，因此，開挖后及時安裝錨索有利于基坑水平位移的控制。如圖4所示，降水過程將會導致明顯的樁體水平位移增加，以降水四為例，開挖四的支護樁水平位移最大值為21.25mm，降水四的樁身水平位移最大值增加至25.20mm，可見降水不利于基坑穩定。此外，樁體水平位移表現出較為明顯的時間效應，在每一個固結期后支護樁水平位移表現出回縮現象，如固結期五后的水平位移最大值回縮約2mm，這是因為隨著時間推移，坑外土體中超靜孔隙水壓力逐漸消散，土體逐漸固結，并且由于時間變化，滲流導致坑內外水頭差逐漸減小，以至于支護樁所受到的水壓力也略有減小，最終導致樁體水平位移略有回縮，這有利于基坑安全和穩定。

TNBC由于缺乏有效的靶向治療位點，盡管患者接受了足劑量的化療，但仍有30%的患者發生遠處轉移[5]。到目前為止，研究顯示ER和PR可作為乳腺癌的獨立預后因子，針對ER和PR的治療也成為乳腺癌一線內分泌治療方案，但是女性體內不光有雌激素，還有雄激素，尤其是絕經后的女性，雌激素大量減少了，而雄激素水平卻無明顯變化。

圖5 為不考慮流固耦合與考慮流固耦合的樁體水平位移對比圖。

圖 5 樁體水平位移對比Fig.5 Pile horizontal displacement comparison

由圖5可知，考慮流固耦合與不考慮流固耦合的最終樁體變形規律相似，最大值均出現在樁體中部，上下端變形較小，但考慮流固耦合時的最終樁體變形與不考慮流固耦合的最終樁體變形相比較大。從受力的角度分析可知，考慮流固耦合的樁體不僅受外側土體的主動土壓力，還受到由于坑內外水頭差引起的滲流力，所以考慮流固耦合的最終樁體變形整體大于未考慮流固耦合的樁體最終變形，但預應力錨索的及時植入可以將變形控制在允許范圍內。

2.2.2 坑外地表沉降

考慮流固耦合的基坑開挖過程坑外沉降曲線如圖 6所示，圖 7為考慮流固耦合與不考慮流固耦合的坑外地表沉降對比圖。

圖 6 考慮流固耦合的基坑坑外地表沉降Fig.6 External surface settlement of foundation pit considering fluid structure coupling

圖 7 基坑坑外地表沉降對比Fig.7 Comparison of surface settlement of foundation pit

由圖 6 可知，沉降分布曲線整體呈凹槽形，隨著開挖深度的不斷增加，沉降最大值也快速增大，并且沉降影響范圍也不斷擴大。開挖結束后，沉降最大值出現在距基坑邊1.4H(H為開挖深度)處，最大值為36.5mm。由圖可知，降水會導致坑外沉降最大值進一步增大，這是由于地下水位下降形成了降水漏斗，降水漏斗以上的土體逐漸固結，導致有效應力增大，從而使得坑外沉降值增大。同時，可以看到，每個固結步的沉降值均小于每個對應的開挖步，這說明坑外沉降也體現出明顯的時間效應。如固結期五坑外沉降回彈現象比較明顯，沉降最大值削減了2.66mm，這是由于隨著時間推移，坑后降水范圍內的土體逐漸固結，負孔壓逐漸消散，導致有效應力略有減小，所以土體沉降有所回彈，這反而對基坑安全是有利的。

由圖 7可知，考慮流固耦合時的最終沉降量遠遠大于不考慮流固耦合時的最終沉降量，并且影響范圍也更大，由于雜填土土質較差，多次開挖及降水導致坑外80m依然有較大沉降，因此設計方案應充分考慮降水對支護結構及周邊環境的影響。這說明降水會使坑外土體沉降明顯增大，這對坑外既有建筑及設施的穩定是非常不利的。因此，降水開挖施工過程中加強坑外沉降監測次數十分必要。

2.2.3 坑底隆起

圖8 為考慮流固耦合的基坑開挖過程隆起圖。

基坑坑底隆起曲線整體呈增長趨勢，在靠近支護樁附近隆起曲線斜率較大，隨著離支護樁越來越遠，曲線漸漸由陡峭變得平緩，并且在基坑對稱面處達到最大值。隨著基坑逐步開挖，坑底隆起最大值由開挖一的19.12mm增長到開挖五的36.55mm，這是因為，基坑的開挖實質是卸載的過程，卸載后導致土體產生方向向上的回彈。降水會導致土體有效應力增大，即降水可以看作加載過程，由圖可知，每個降水步與它所對應的上一個開挖步相比，隆起量明顯有所下降，其中，開挖一隆起量最大值為19.12mm，而降水一隆起量最大值下降至9.48mm。基坑坑底隆起也表現出了明顯的時間效應，但規律卻和坑外沉降及樁體水平位移相反，從圖8可以觀察到，每個固結期的隆起曲線都在其對應的開挖步隆起曲線之上，這是因為隨著時間變化，土體逐漸固結，負孔壓慢慢消散，有效應力減小，相當于卸載過程，最終導致固結期后的隆起量大于開挖步，這對坑底隆起穩定性十分不利。

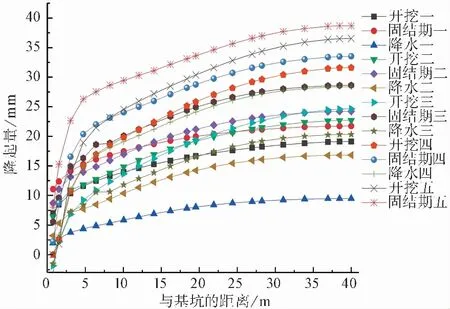
圖 8 考慮流固耦合的基坑坑底隆起Fig.8 Uplift of foundation pit bottom considering fluid structure coupling

圖9 給出了考慮流固耦合與不考慮流固耦合兩種情況下開挖結束后的坑底隆起對比圖。

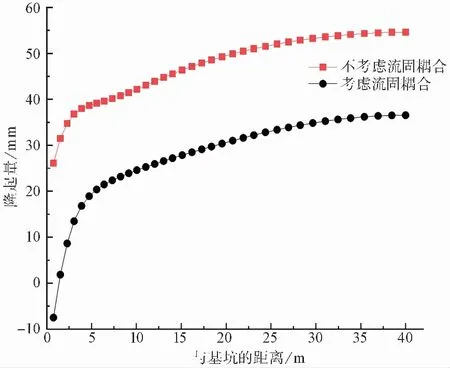
圖 9 基坑坑底隆起對比Fig.9 Comparison of uplift at the bottom of foundation pit

由圖 9 可知，考慮流固耦合的最終隆起量與不考慮流固耦合的最終隆起量都呈現出隨距離基坑側壁越遠，而逐漸增大的趨勢，并且兩者都在基坑對稱面上達到最大值。對比圖 9兩條隆起曲線大小關系可知，基坑降水對坑底隆起具有明顯的削弱作用，這種削弱作用致使考慮流固耦合的基坑底部隆起量總是小于未考慮降水的隆起量。這種規律也能體現在樁體豎向位移上，根據模擬數據，考慮降水時的樁體豎向位移為-25.2mm，不考慮降水時樁體豎向位移為5.4mm。此外，距離支護樁越近，坑底隆起量越小，說明支護結構對基坑底部隆起會產生明顯的限制作用。

2.3 考慮流固耦合與不考慮流固耦合的內力對比2.3.1 彎矩對比

圖10 所示為考慮流固耦合與不考慮流固耦合兩種情況下開挖結束后的樁體彎矩圖。

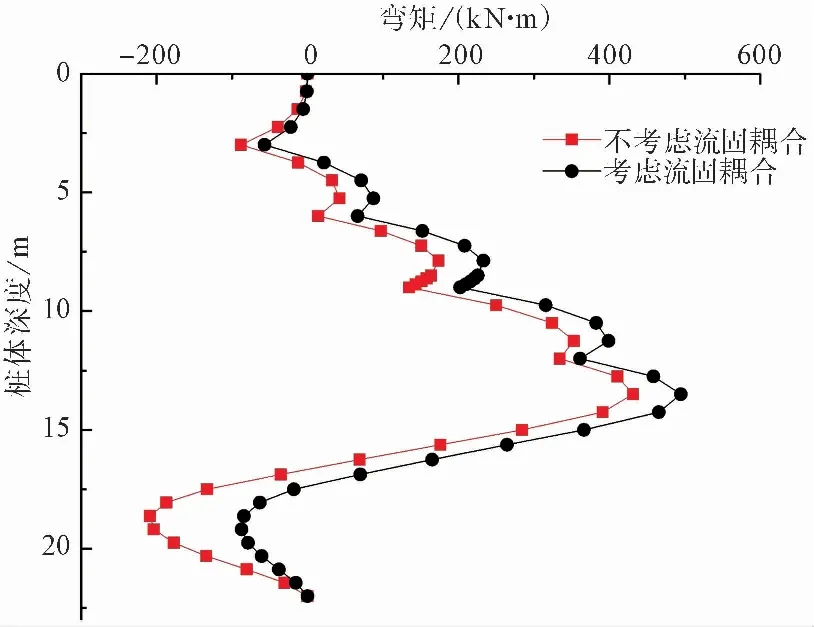
圖 10 彎矩對比Fig.10 Moment comparison

比較兩種情況的計算結果，可知兩條曲線都呈現出相似的變化規律，最大負彎距出現在坑底以下4.2m處，最大正彎矩出現在距樁頂12m處，并且在施作錨桿的位置，彎矩圖產生突變。另一方面，考慮流固耦合的彎矩在坑底以上總是大于未考慮流固耦合的彎矩，正彎矩最大值相差64kN·m，在坑底以下規律恰好相反。這是由于降水產生的滲流力在坑外方向是向下的，在坑底方向是向上的，導致坑外土體主動土壓力增大[15]，坑內土體被動土壓力減小，即降水對土體的應力場產生了影響，導致了彎矩的變化。

2.3.2 軸力分析

表 4為考慮流固耦合與未考慮流固耦合的錨索軸力對比。可知，考慮流固耦合與不考慮流固耦合兩種情況下，都是第三道錨索軸力最大，第一道錨索和第四道錨索軸力較小。另外，考慮流固耦合的最終軸力總是小于不考慮流固耦合的軸力，這是由于坑內降水導致坑內外產生水位差，使得坑外地下水位面發生傾斜，而4道錨索的錨固段長度較長，均穿過了傾斜的地下水位面，土體參數發生改變，尤其黏聚力和內摩擦角的變化讓錨固段錨固性能有所削弱，導致錨索軸力相對于未考慮流固耦合而言有所下降。這種現象在第一排錨索表現得最為明顯，其他三排錨索軸力也有小幅度的下降。

表 4 錨索軸力對比Table4 Axial force comparison of anchor cable

3 結論

(1)在樁錨支護深基坑降水開挖過程中，由于土體中超靜孔隙水壓力隨時間逐漸消散，基坑變形表現出較為明顯的時間效應。樁體水平位移和坑外地表沉降在開挖后設置的固結期產生了回彈現象，但固結期的隆起量相對于開挖后有所增大。

(2)考慮流固耦合與未考慮流固耦合計算結果相比，樁體水平位移和坑外地表沉降都明顯增長，坑底隆起卻明顯減小，這說明降水對于坑內隆起穩定性是有利的，對坑外土體和樁體水平位移是不利的。另一方面，由于樁土相互作用，降水對樁體豎向位移和坑底土體隆起有類似的影響，并且樁體對坑底隆起具有削弱作用。

(3)從內力方面進行對比分析，樁體彎矩在坑底以上部分，考慮流固耦合時更大，而坑底以下部分，考慮流固耦合時彎矩卻小于未考慮流固耦合時彎矩。另外，考慮流固耦合時的最終軸力小于不考慮流固耦合時的最終軸力，這是因為考慮流固耦合時錨固段穿過了傾斜的地下水位面，土體參數的改變讓錨固段錨固性能有所削弱，導致錨索軸力相對于未考慮流固耦合而言有所下降。

(4)經過分析，得出地下水位較高的深基坑支護設計一定要考慮降水滲流帶來的影響，這樣設計方案才能更加安全。在施工階段，要充分考慮時間因素對開挖變形的影響，應該在開挖完成后及時施作錨桿(錨索)，并適當增加監測頻次，有利于防止基坑變形失控。

(5)有限元數值模型能反映出工程實踐規律，是省時省力且比較經濟的一種研究方法，但由于地質的復雜性及施工過程的不確定性，數值計算大小僅供參考。