高馬赫數低雷諾數條件下圓球繞流曳力系數

李瑞元，陳飛國，葛 蔚，張永民

(1. 中國科學院過程工程研究所 多相復雜系統國家重點實驗室，北京 100190；2. 中國石油大學（北京） 重質油國家重點實驗室，北京 102249；3. 中國科學院 綠色過程制造創新研究院，北京 100190；4. 中國科學院大學 化學工程學院 北京 100049)

0 引 言

圓球繞流曳力系數（drag coefficient，CD）是流體力學研究的重要基礎問題，其可作為量化指標廣泛應用于航空航天、醫藥加工、石油化工及能源工業等領域中。

在通常的不可壓縮連續流體中，圓球繞流曳力系數CD被認為是雷諾數（Reynolds number，Re）的函數，一百多年來的國內外學者也對此進行了詳盡研究。而在飛行器涉及的高速高空環境中，往往伴有高馬赫數的可壓縮性以及高努森數條件下的稀薄效應，CD不僅與Re相關，還與馬赫數（Mach number，Ma）或者努森數（Knudsen number，Kn）相關。

高馬赫數條件下圓球繞流曳力系數CD的研究主要有地面實驗[1-13]和數值模擬[14-19]等方法。實驗方法又可分為直接測量和間接計算兩種方式。直接測量是指在風洞實驗中通過測量細線懸掛球體偏轉角度或金屬支撐球體受力計算球體的CD[1,2,4,8-11,13]。1961年Peter等[10]在干燥的空氣中用細線懸掛球體，測量偏轉角度來計算圓球受流體作用力，獲得了3.8 ＜Ma＜ 4.3，50 ＜Re＜ 1 000范圍內圓球繞流的CD值。1962年Aroesty[9]采用相似的方法在伯克利低密度風洞中測量得到了2 ＜Ma＜ 6，10 ＜Re＜ 10 000范圍內的CD。間接計算是指通過彈道的形式發射物體，獲得位置與時間的關系，從而求解獲得CD[3,5-7,12]。1967年Short等[7]通過彈道實驗測量獲得了0.4×106＜Re＜ 1.6×106，0.4 ＜Ma＜ 14.5范圍內圓球繞流的CD。1968年Crowe等[5]通過彈道實驗獲得了0.01 ＜Re＜ 5.1，0.036 ＜Ma＜ 1.77范圍內圓球繞流的CD。1972年Bailey[3]發射泡沫塑料球至干燥空氣中，記錄不同時刻球的位置，計算得到球體的CD。

風洞及彈道實驗獲得的CD結果較為可信，但其成本高昂，測量過程易受其他因素影響，誤差較大且難以獲得流場的細節特征。隨著計算機技術和流體力學計算方法的發展，數值模擬作為一種可信的方法被用來研究圓球繞流。

Tao等[14]用格子玻爾茲曼方法（lattice Boltzmann method, LBM）模擬研究了0.1 ＜Re＜ 3.5和0.1 ＜Kn＜ 1.1條件下的圓球繞流。Nagata等[15]采用計算流體力學（computational fluid dynamics，CFD）方法，模擬研究圓柱區域中50 ＜Re＜ 300和0.3 ＜Ma＜ 2條件下的圓球繞流，并獲得了豐富的繞流尾跡特征。Dogra等[19]使用直接數值模擬蒙特卡洛方法（direct simulation Monte Carlo, DSMC）研究了Re＞ 100和Kn＜ 0.1條件下的圓球繞流。

我們整理了文獻中不同Re和Ma下的CD數據，繪制于圖1中。可以發現，文獻中CD數據較為分散，不同文獻中的變化規律有時還有所差異；另外，在1≤Re≤20和0.1≤Ma≤3這一趨勢變化劇烈的范圍內，特別在1≤Re≤10和0.5≤Ma≤3高馬赫數低雷諾數區間內，文獻中CD數據不全，難以準確揭示該范圍內的CD與馬赫數的變化規律。

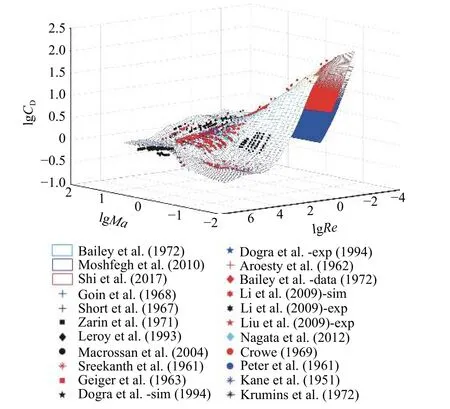
圖1 圓球繞流曳力系數Fig. 1 A compilation of drag coefficients of flows past a sphere

在高馬赫數低雷諾數條件下，努森數Kn較大，氣體流動為過渡流（0.1≤Kn≤10）或者分子流（Kn≥10）。該狀態下實驗測量困難，而基于連續流體的CFD方法難以適用，LBM方法的玻爾茲曼方程適合描述Kn≥10的流體，分子動力學（molecular dynamics, MD）方法計算精確但計算需求極大。

葛蔚等[20-21]提出的擬顆粒模型（pseudo-particle model，PPM）將軟球模型的時驅算法結合到硬球模型（hard sphere，HS）中，具有MD計算精確和DSMC計算高效的優點，同時PPM采用時間驅動，提高了計算可擴展性。在PPM中，兩個擬顆粒在接觸碰撞時距離會稍小于粒子直徑，將碰撞時距離的統計平均作為粒子有效直徑，此時擬顆粒性質就能與硬球顆粒等效，即擬顆粒模型可以視作一種可變徑硬球模型。沈國飛和葛蔚[22]將HS與 PPM 耦合建立了硬球-擬顆粒方法（HS-PPM）：在各子區域內部采用HS模擬流場，而用PPM模擬邊界區域，在保證碰撞精確性的同時解決了傳統HS不易擴展的問題，便于大規模并行計算。HS-PPM為高馬赫數低雷諾數條件下的圓球繞流研究提供了合適的模擬計算方法。

本文計劃應用HS-PPM方法模擬1≤Re≤20和0.1≤Ma≤3條件下圓球繞流過程，獲得的曳力系數數據用于初步分析CD(Re,Ma)。

1 圓球繞流HS-PPM模擬

HS-PPM耦合方法模擬圓球繞流示意于圖2中，其中U表示來流氣速，L為模擬區域長度，H為高度，W為寬度，L1為圓球離入口距離。

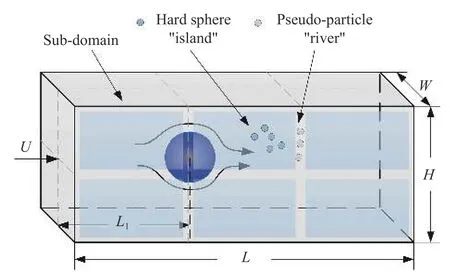
圖2 圓球繞流模擬示意Fig. 2 A sketch of the numerical simulation of a flow past a sphere

本文分別將氣體粒子的質量、直徑作為質量、長度單位，擬顆粒更新時間步長為1個時間單位。

1.1 HS-PPM方法

在HS-PPM耦合方法中，HS用于精確計算粒子碰撞，而PPM有效擴展計算規模。兩個粒子是否發生碰撞的判據表述為兩粒子間距離|r1-r2|小于它們的半徑之和以及r1-r2與v1-v2的點積為負值，則它們將以光滑硬球方式碰撞。

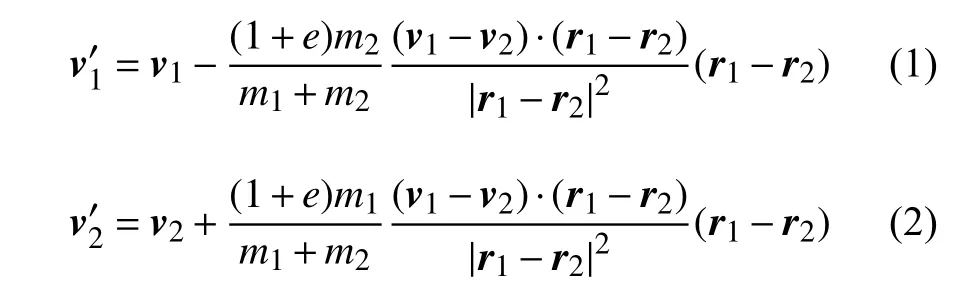
根據模擬需要將區域劃分為Nx×Ny×Nz個子區域，每個子區域內部采用HS，邊界區采用PPM連接各HS模擬區域，示意于圖2中。每個進程負責一個子區域內計算，相鄰進程間構建一層虛擬緩沖區由消息傳遞接口（message passing interface，MPI）協議實現信息交換。

1.2 氣體-圓球作用

運動的氣體粒子與圓球發生接觸時其路徑會發生變化，涉及的氣體-圓球間作用通常采用反彈或漫反射方式處理。反彈模型中入射粒子速度法向分量沿法線反轉，切向分量保持。漫反射模型中出射粒子速度遵循給定溫度下的偏麥克斯韋分布，與入射速度無關，具有完全熱適應能力。在高馬赫數流動中，實際氣體粒子與圓球的作用同時結合了上述兩種方式，引入熱適應系數α（0≤α≤1）來描述[23]，即粒子的出射速度中α部分來自于偏麥克斯韋分布的漫反射，（1-α）部分采用反彈模型。

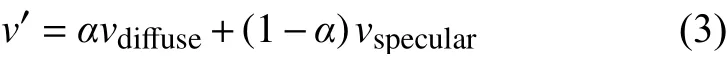
1.3 邊界設置

如圖2所示，氣體從左邊以速度U均勻流入模擬區域，從右邊出去的氣體粒子將在左邊控制區內應用速度重新標定控溫法[20-21]被賦予初速U重新生成，而上下和前后方向采用周期性邊界條件，保證氣體粒子數守恒。控制區厚度為1，沿y方向和z方向被分割成4Ny×4Nz個子區。這樣處理后，氣體的流動長時間演化達到穩態狀態。

1.4 曳力系數的計算

氣體粒子與圓球之間的每次碰撞均會對圓球產生一個沖量，則在一定時間段內統計這些沖量得到圓球受到氣體的平均作用力FD為：

其中P2-P1表示T2-T1時間內動量改變量的累加值。圓球繞流的曳力系數CD計算公式為：

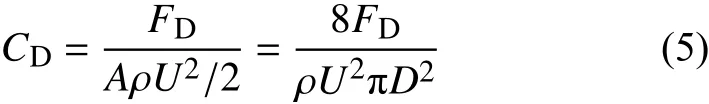
其中D為圓球直徑。

在本文涉及的條件下，體系運行1×106時間后流動達到穩定，隨后開始統計計算曳力系數，統計持續時間為4×106（Re＜15）或1×106（Re≥15）。

2 結果與討論

圓球繞流HS-PPM模擬得到的CD不僅與Re和Ma相關，還受到模擬設置的影響，主要包括模擬區域設置和熱適應系數α。因此本部分首先考察模擬區域設置和熱適應系數等模擬設置對CD的影響規律，從而獲得合理的模擬設置用于1≤Re≤20和0.1≤Ma≤3條件下圓球繞流CD數據的補充和分析。

2.1 曳力系數模擬計算

以Re= 19.4和Ma= 1.195條件下的圓球繞流模擬為例，說明曳力系數的計算過程和誤差分析。在L×W×H= 276.8×276.8×276.8區域內用3.24×106氣體粒子，模擬了Re= 19.4和Ma= 1.195條件下的圓球繞流過程，記錄不同時間段內的氣體粒子與圓球間碰撞信息，用于曳力系數計算，結果如圖3所示。從圖3中可以看到，模擬計算的曳力系數在1×106時間后趨于定值。在計算曳力系數的1×106到2×106時間內，氣體粒子與圓球之間發生1.42×106次碰撞，則曳力系數的統計誤差在0.1%以下。

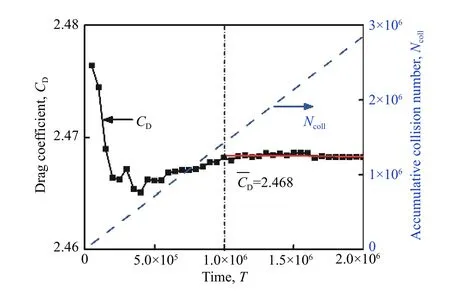
圖3 Re = 19.4和Ma = 1.195，隨時間變化的曳力系數和累積碰撞數Fig. 3 Temporal evolutions of the drag coefficient and accumulative collision number at Re = 19.4 and Ma = 1.195

圓球繞流曳力系數的計算精度還與流場是否充分發展相關，因此比較了三個不同條件下的圓球繞流流場模擬結果，見圖4。從中可以發現：隨著Re增大，尾流在圓球后部逐漸分離，形成對渦（圖4（b））；當Ma＞ 1時，在圓球前面形成激波，此時需要更寬的模擬區域用于激波面往兩側發展（圖4（c））。這些發現與文獻[22，24]中的結果較為相符。

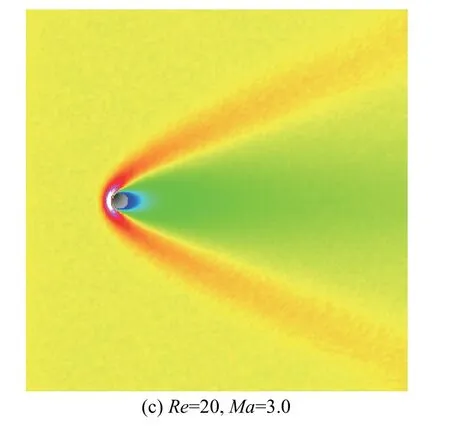
圖4 中間截面上的密度云圖和流線示意Fig. 4 Density contours and streamlines in the middle plane

2.2 模擬區域的影響

圓球繞流HS-PPM模擬在一個有限空間內進行，獲得的結果通常會與無限大流場內圓球繞流有差異，因此有必要討論如何設置模擬區域使偏差在合理范圍內。

在一定的Re和Ma條件下，分別改變模擬區域長度、寬度（高度）以及圓球位置，作了一系列圓球繞流HS-PPM模擬，其中長度或寬度范圍為5D～40D，圓球位置為長度的0.25處、0.38處和0.5處。

圖5表示Re= 19.4和Ma= 1.195條件下，CD模擬結果隨長度或寬度的變化趨勢。從圖中可以看到，隨著長度或寬度的增大，CD逐漸趨于穩定值CD∞，且在20D后CD與CD∞偏差較小。圖5還顯示了該條件下CD實驗值處于熱適應系數α= 0及α= 1下的兩個CD∞之間，從另一個角度論證了HS-PPM模擬獲得圓球繞流CD的合理性。

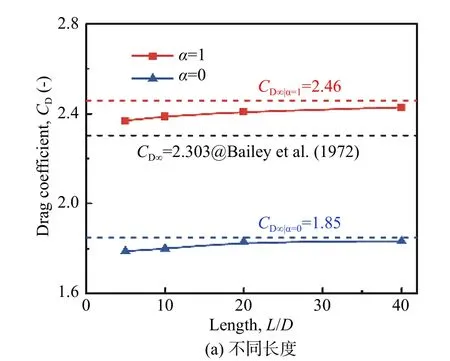
進一步模擬研究發現：Ma＜ 1和Re＜ 10時，CD與模擬區域的相關性較小；Ma＜ 1和Re＞ 10時，隨著Re的增大，圓球繞流逐漸不穩定，需要適當增大區域長度滿足尾跡的發展；Ma＞ 1和Re＜ 10時，圓球前方流體出現激波面，此時需要增大區域寬度（高度）用于激波面的發展；Ma＞ 1和Re＞10時，模擬區域長度和寬度（高度）均需要增大。基于上述認識，我們給出了不同條件下模擬區域的建議設置，列于表1中。并按照建議的區域設置模擬了不同Re和Ma下的圓球繞流，得到的CD結果與CD∞偏差在2%以內（見表2），表明有限區域的模擬結果可以近似表達無限區域內圓球繞流。

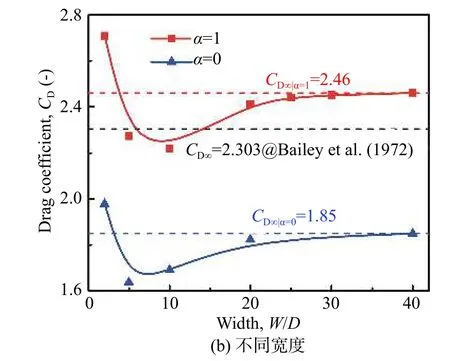
圖5 Re= 19.4和Ma = 1.195，不同長度和寬度的CDFig. 5 The variation of drag coefficient with the lengths and widths of the simulation domain at Re = 19.4 and Ma = 1.195

表1 合適的模擬區域Table 1 Appropriate simulation domains under different conditions

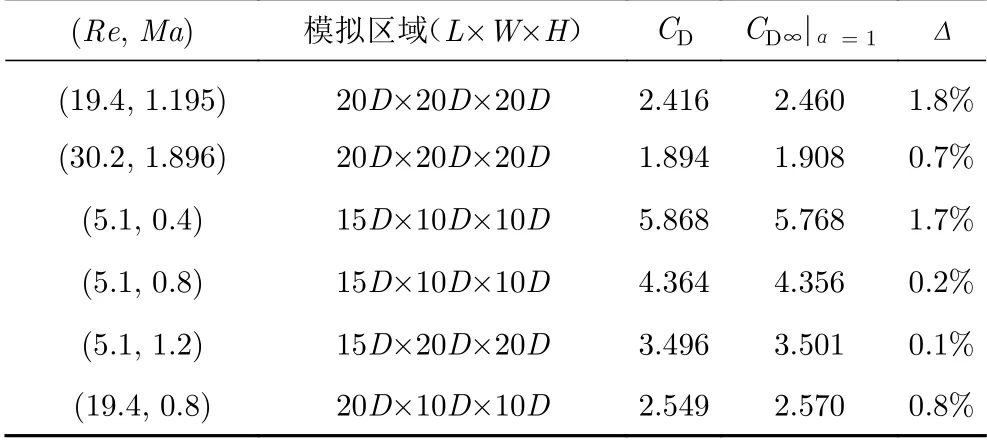
表2 不同條件下CD模擬結果Table 2 Drag coefficients at different Re and Ma

2.3 熱適應系數的影響

在高馬赫數下稀薄效應明顯，氣體-圓球間通常介于無滑移條件和完全滑移條件之間，HS-PPM模擬圓球繞流引入熱適應系數α來表達氣體-圓球間作用中漫反射成分：α= 0時，鏡面反彈滑移；α= 1時，完全漫反射。而α的不同取值會對CD結果造成影響，佐證于圖5中。趙琪和馬琳博等[23-24]已對此進行了初步分析，發現圓球繞流CD模擬值與熱適應系數α正相關。

基于上述發現，將不同α下的CD與實驗結果進行比較，獲得兩者偏差最小的熱適應系數合理值αr。圖6表示Re= 5.1和Ma= 0.4條件下不同α模擬得到不同CD，可以發現CD與α的關系呈顯著的線性關系，CD=1.78α+4.16（R2= 0.998），進而得到CD與實驗值相符的αr= 0.643。類似地，完成了Re= 19.4和Ma=1.195、Re= 30.2和Ma= 1.896條件下的CD與α的關系研究，獲得對應的αr，結果列于表3中。采用αr作了驗證性模擬，獲得的CD與實驗值偏差在1%以內。

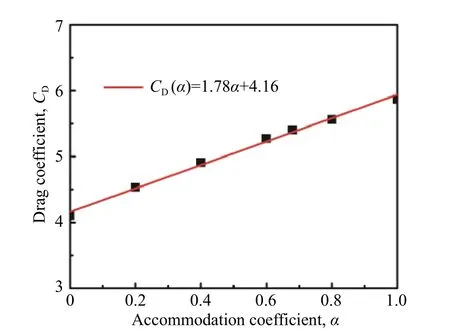
圖6 Re = 5.1和Ma = 0.4，CD與α的關系Fig. 6 The variation of drag coefficient with α at Re = 5.1 and Ma = 0.4

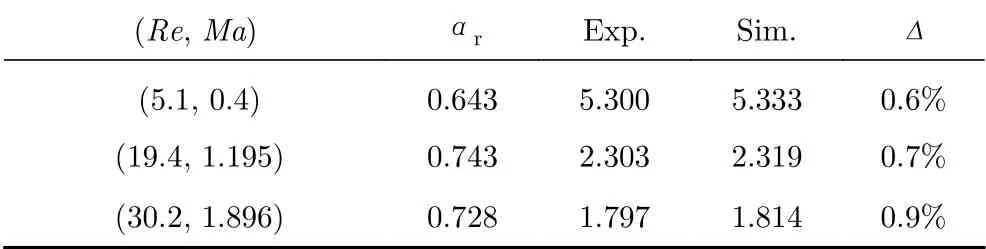
表3 不同條件下的熱適應系數合理值αrTable 3 Reasonable accommodation coefficients αr at different Re and Ma

不同Re和Ma條件下的αr存在一定的差異，表3也表明αr約在0.65-0.75之間，將αr統一設置為0.7可以平衡精度和嚴格驗證所需的大批量模擬需求。我們采用αr= 0.7模擬計算得到其他條件下的CD，并與相應的實驗值比較，結果列于表4中。可以發現，αr=0.7時的模擬值與實驗值偏差均較小（5%以內），故后續模擬均采用αr= 0.7。

2.4 1≤Re≤20和0.1≤Ma≤3的曳力系數CD

在得到合適的區域設置條件和熱適應系數后。應用HS-PPM模擬圓球繞流獲得了1≤Re≤20，0.1≤Ma≤3范圍內的曳力系數CD，結果繪制于圖7中。詳細的模擬參數和結果列于附錄A的表格中。

表4 α = 0.7, 不同條件下CD模擬結果Table 4 Drag coefficients at α = 0.7

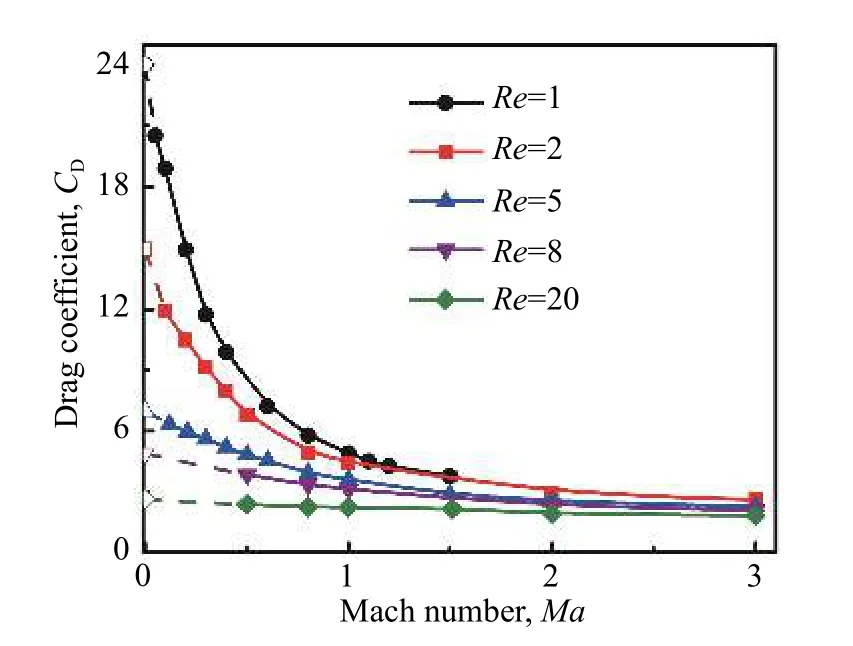
圖7 1≤Re≤20時，CD與Ma的關系Fig. 7 The variation of the drag coefficient with Ma at 1≤Re≤20

圖7中的實心點表示HS-PPM模擬計算得到的CD，空心點表示Ma→0條件下標準阻力系數CD(Re)。從圖7中可以看出，在1≤Re≤20范圍內，CD隨著Ma的增加而逐漸下降；Re越大，CD下降趨勢趨緩。

馬赫數Ma對CD(Re)的修正可以表達為下面形式，

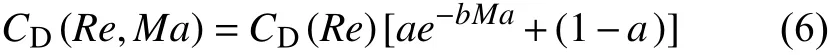
其中[ae-bMa+ (1-a)]為曳力系數修正項，系數a和b與Re相關。

按照公式(6)擬合CD數據得到了不同Re下的系數a和b（列于表5中），并將系數a和b分別擬合成Re的函數（如圖8）。

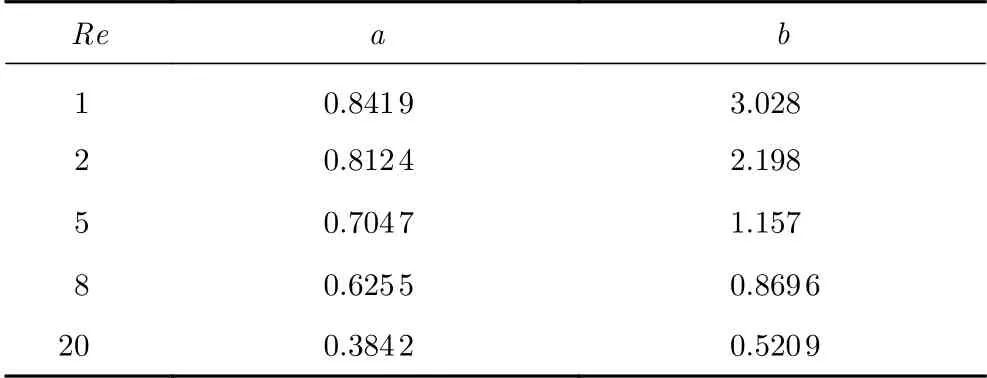
表5 不同Re下的參數a和bTable 5 Parameters a and b at different Re

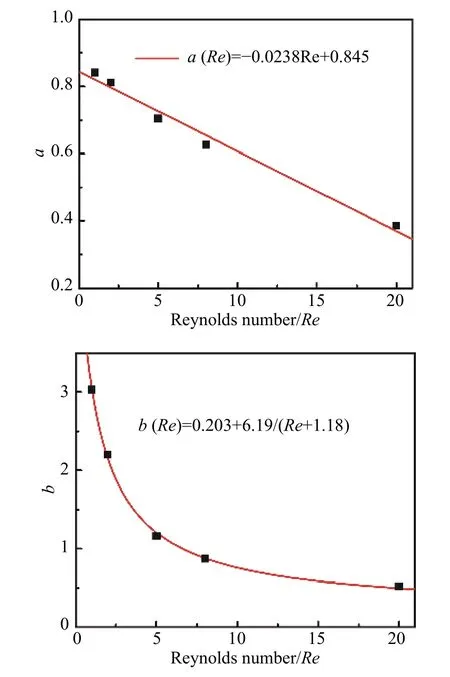
圖8 參數a，b與Re的關系Fig. 8 The variations of the parameters a and b with Re

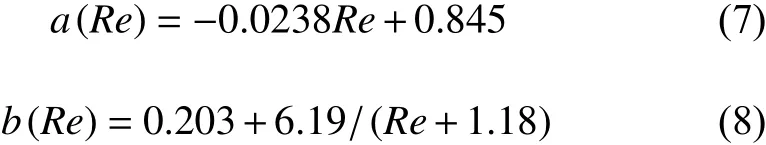
3 結 論

本文應用HS-PPM方法模擬了1≤Re≤20和0.1≤Ma≤3條件下的圓球繞流過程。在討論確認合理的模擬區域設置和熱適應系數αr= 0.7后，獲得不同Re和Ma下的圓球繞流曳力系數CD數據，并基于此建立高馬赫數低雷諾數條件下馬赫數Ma對CD(Re)的修正模型，

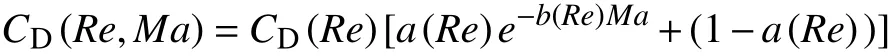
其中，

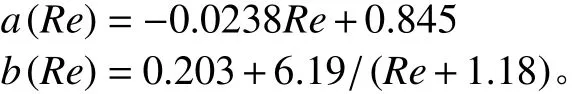
高馬赫數下圓球繞流流動形態復雜，本文僅對1≤Re≤20和0.1≤Ma≤3范圍內的圓球繞流曳力系數作了定量分析，而其他范圍內的曳力系數變化趨勢仍難以用統一的方式進行描述。此外，高馬赫數特別是Ma＞ 3條件下，激波的存在和發展對圓球繞流流動形態影響巨大，而且會發生強烈的高速熱效應，這些都會對曳力系數的計算產生重要影響，需要進一步深入研究。