基于零部件均衡重要程度的混流裝配線排序

劉 暢，原丕業，劉佳楠，張 萌

(青島理工大學 管理工程學院，山東 青島 266520)

混流裝配線是指在同1條裝配線上以流水作業的方式混合連續地完成工藝接近的不同類型、不同數量的產品。合理的產品投放順序有助于降低成本、提高效率，進而提升企業的競爭力。因此，眾多學者針對該問題進行了大量的研究。文獻[1-7]分別從不同的角度建立關于混流裝配線的排序模型，但并未考慮到生產過程中零部件消耗的均衡化。文獻[8-14]雖在建立的混流裝配線排序模型中考慮到零部件消耗均衡化的因素，但并未考慮到不同類型零部件的消耗均衡情況對生產裝配系統重要程度的差異性。因此，在以零部件消耗均衡化為目標的混流裝配線排序過程中考慮零部件均衡化的重要程度是十分必要的。

1 問題描述

混流裝配線排序問題是一個短期決策問題，每日甚至每班都需要根據市場需求的變化安排合適的排產計劃。由于在混流裝配線中生產每種產品所需的零部件類型以及數量各不相同，所以不同的投產排序對各類零部件的消耗都是不同的。若零部件消耗不均衡，則會造成在一段時間內某類零件的需求量激增，而其他零件的需求量較少，為了應對某零件的高峰需求，該零件需要維持在1個較高的安全庫存，從而造成不必要的浪費。因此，在混流裝配線排序時需要對零部件消耗波動進行均衡。由于傳統的零部件消耗均衡是為了達到總體目標的最優，即全部零部件消耗波動函數之和最小化，所以個別類型的零部件消耗波動均衡情況一定沒有或者是較小地進行改善。若這類零部件的均衡程度相對生產系統更為重要，則必須采用一定的方法保證這類零部件最大程度地優先進行均衡。

2 數學建模

基于以上描述，為了確保重要零部件最大程度地優先進行均衡，本文根據各類零部件均衡對生產裝配系統的重要性，分別賦予各類零部件不同的權重，為了簡化運算，在1個最小生產循環內構建基于零部件均衡重要程度的混流裝配線排序模型

(1)

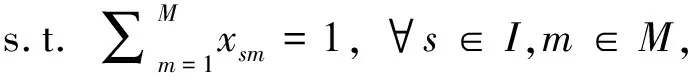
(2)

(3)

qms-qm,s-1≤1， ?s∈I,m∈M，

(4)

qms-qm,s-1≥0， ?s∈I,m∈M，

(5)

0≤qms≤dm， ?s∈I,m∈M，

(6)

0≤ωg≤1， ?g∈p.

(7)

式中：I為1個MPS中需要排序的產品數量；s為排產序列中第s個位置；p為零部件的種類數量；M為產品的種類數量；g為類型g的零部件；m為類型m的產品；dm為類型m的產品數量；ngm為裝配產品m所消耗零部件g的數量；qms為前s個位置中產品m的數量；ωg為零部件g均衡化重要程度的權重；xsm為0～1變量，當排產序列中第s個位置的產品是m，則為1，否則為0。

目標函數表示考慮零部件均衡重要程度的零部件消耗均衡情況，其中，括號內第一部分表示零部件的理想消耗量，第二部分表示零部件的實際消耗量；式(2)表示任意1個位置只能安排1個產品；式(3)表示排產序列中安排m產品的數量等于其需求量；式(4)、式(5)表示在任意1個s-1的位置到s位置，產品m的數量只能增加1或保持不變；式(6)表示排序中任意s位置前產品m的數量不能大于1個MPS中產品m的需求量；式(7)表示權重的取值范圍。

3 自適應遺傳算法的設計

遺傳算法是由美國教授Holland在1975年提出的1種效仿達爾文生物進化過程的優化算法，即通過對染色體的評價、選擇、交叉以及變異等一系列操作，最終得到最優的目標值。但是，傳統的遺傳算法中的交叉算子和遺傳算子往往采用固定的數值，這種方式的弊端在于若種群中出現占據絕對優勢的染色體，極易導致求解的結果陷入局部最優。為了避免出現早熟現象，提高全局搜索最優染色體的能力，文中設計新的自適應遺傳算法用于解決混流裝配線的排序問題。該算法在遺傳算法的基礎上通過借鑒文獻[15]的自適應機制對交叉和變異算子進行動態地調整，可以使模型在求解過程中有效地避免出現早熟的現象。綜合以上的分析，可得到本文設計的自適應遺傳算法的流程如圖1所示。

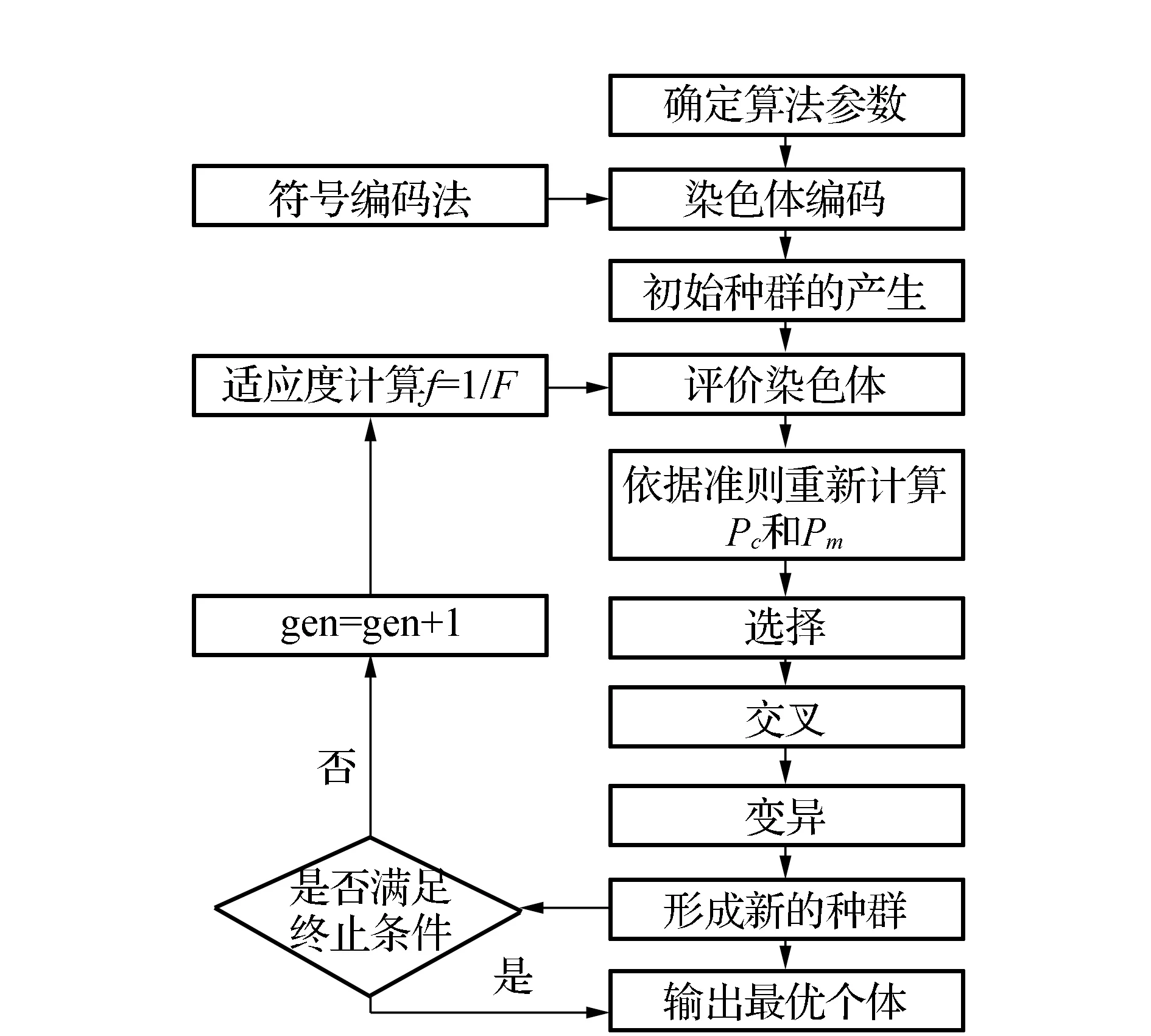
圖1 自適應遺傳算法流程

3.1 編碼

針對投產排序問題，由于模型的求解結果只與產品對應編碼在染色體上的位置有關，與其大小無關，故本文采用符號編碼方式。不同類型的產品用不同的數字表示，如A，B，C，D，E 5種產品分別用1，2，3，4，5進行表示，則染色體11223345解碼后可表示為AABBCCDE這樣一個序列依次進入裝配線。

3.2 初始化種群的產生

為了確保初始解的質量以及多樣性，在初始化種群的過程中參考小生境技術先進的思想。首先依據1個MPS中各產品的投產比例，分別確定染色體的長度以及種群的規模，然后任意生成滿足種群規模大小條件的若干個種群，挑選出每個種群中適應度值排名前10%的染色體，使其組成1個新的種群，最終形成初始種群。

3.3 選擇

為了能夠更好地選擇和保留優秀的染色體，本文采用精英保留策略和輪盤賭相結合的方法。采用輪盤賭的方法雖然可以使適應度值好的染色體有較大的概率被選中復制到下一代，但是無法保證一定被保留。同理，適應度值較差的染色體無法保證被淘汰。并且由于后續交叉和變異的過程中具有隨機性，容易出現遺傳退化。因此，為防止出現遺傳退化解，確保淘汰最差個體，保留最優染色體，故在輪盤賭的基礎上加入精英保留策略。即保存并記錄父代種群中的最佳染色體，若子代種群相比父代種群沒有出現更優秀的染色體，則用保存的最佳染色體替換子代種群中適應度值最低的染色體，否則，將更新當前保存的最佳染色體。

3.4 自適應交叉算子

交叉概率決定了種群中染色體被選中進行交叉從而產生子代的概率，小的交叉概率能夠更好地對種群中出現的優秀個體進行保留，但是容易陷入局部最優。大的交叉概率有利于跳出局部最優從而尋求最優解，但是會損害優秀個體，造成算法退化，為了提高算法對局部最優的突破能力以及全局最優的保存能力，借鑒文獻[10]的方法，通過評價當前種群染色體的離散程度對交叉概率進行自適應調整,具體計算如式(8)所示。從選擇復制產生的子代種群中按照自適應交叉概率pc選取一定數量的交叉父本，兩兩父代個體之間進行交叉操作。交叉過程如圖2所示：首先從父代1中任取一段基因直接遺傳到子代1相應的位置；其次，從父代2中依次剔除所選取片段中含有的基因，并將殘留的基因依次遺傳到子代1剩余的位置中，從而產生新的子代個體。同理，交換父代的位置可產生子代2。將從原種群中選擇的交叉父本分別用新產生的子代個體進行替換，進而形成新的種群。

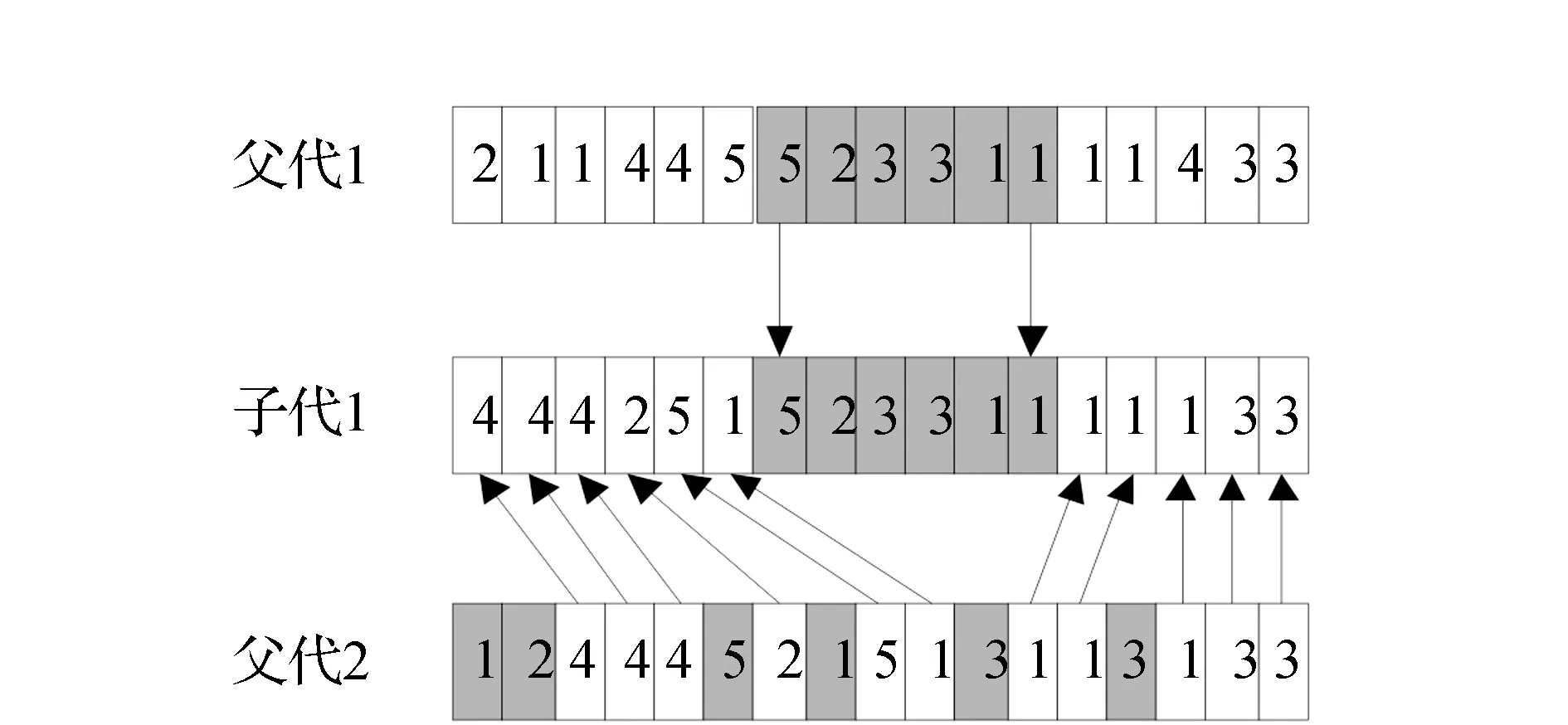
圖2 交叉過程

自適應交叉概率pc的計算公式為

pc=

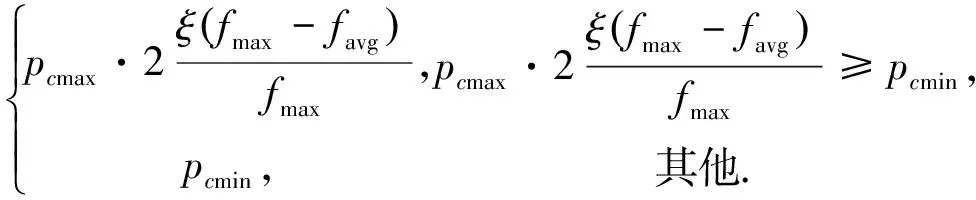
(8)

式中：pcmax為預設最大交叉概率；pcmin為預設最小交叉概率；fmax為當前種群內個體的最大適應度值；favg為當前種群內各個體的平均適應度值；ξ為fmax-favg的敏感性系數。

3.5 自適應變異算子

變異概率決定了種群中染色體被選中進行變異的概率，對種群多樣性的保持有著重要意義。本文通過借鑒文獻[10]的方法對變異概率進行自適應調整，具體計算如式(9)所示。變異過程具體如下：首先從種群中按照自適應變異概率抽取一定數量的變異父本，其次如圖3所示對變異父本中的染色體隨機選取兩個需要突變的位置進行交換以完成變異操作。

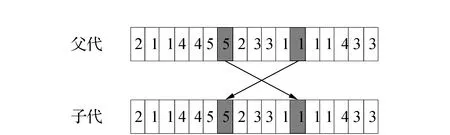
圖3 變異過程

自適應變異概率pm計算公式為

pm=

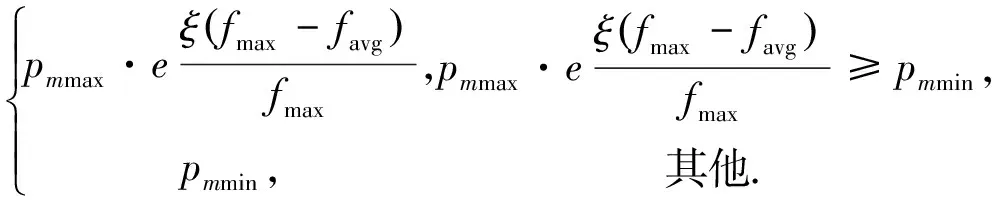
(9)

式中：pmmax為預設的最大變異概率,pmmin為預設的最小變異概率。

根據式(8)和式(9)可知，fmax與favg的差值越大表示當前種群個體越離散，種群多樣性越好，此時需要降低交叉概率pc和變異概率pm，從而加速收斂。fmax與favg的差值越小表示當前種群個體越集中，多樣性越差，為防止出現局部收斂等問題，需要增加交叉概率pc和變異概率pm。

4 案例分析

已知某公司混流裝配線上A，B，C，D，E 5種產品的日均訂單需求量分別為(60，20，40，30，20)，根據最小生產循環原理可得到A，B，C，D，E的產品比例為6:2:4:3:2，現階段公司按照AAAAAABBCCCCDDDEE的順序在最小生產循環內依次對各類產品進行小批量生產，其中，每種產品消耗零部件的類型和數量如表1所示。

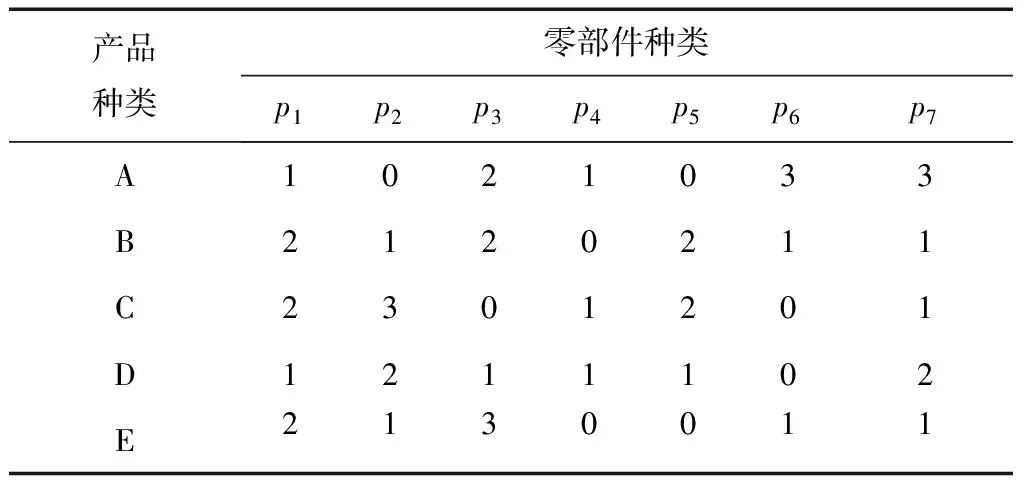
表1 產品-零部件消耗矩陣

本文的算法通過MATLAB R2016a進行編程，計算機處理器參數為Intel(R)Core(TM)i5-8250U CPU@1.6 GHz 1.80 GHz雙核處理器，RAM為8 GB，64位Windows10操作系統。經過算法靈敏度計算實驗，確定涉及的參數設置如下：種群大小為30，最大交叉概率與最小交叉概率分別為0.9和0.5，最大變異概率與最小變異概率分別為0.1和0.01，迭代代數為100，ξ為10，根據各零部件均衡化重要程度確定權重ωg=[0.4,0.4,0.4,0.4,1,1,0.4]。

4.1 算法對比

利用自適應遺傳算法進行求解，得到最終的混流裝配線排序方案為DABCAECADACACEBAD，目標函數值為31.282 4。其中，自適應遺傳算法收斂曲線如圖4所示。

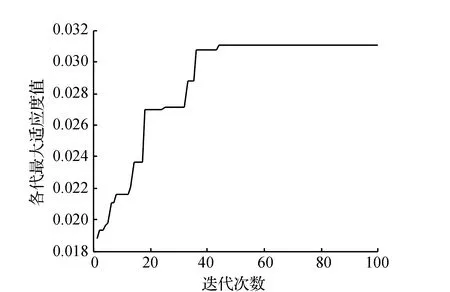
圖4 自適應遺傳算法收斂曲線

利用標準遺傳算法進行求解，得到最終的混流裝配線排序方案為DABCAECAEDACDACAB，目標函數值為39.411 8。其中，標準遺傳算法收斂曲線如圖5所示。

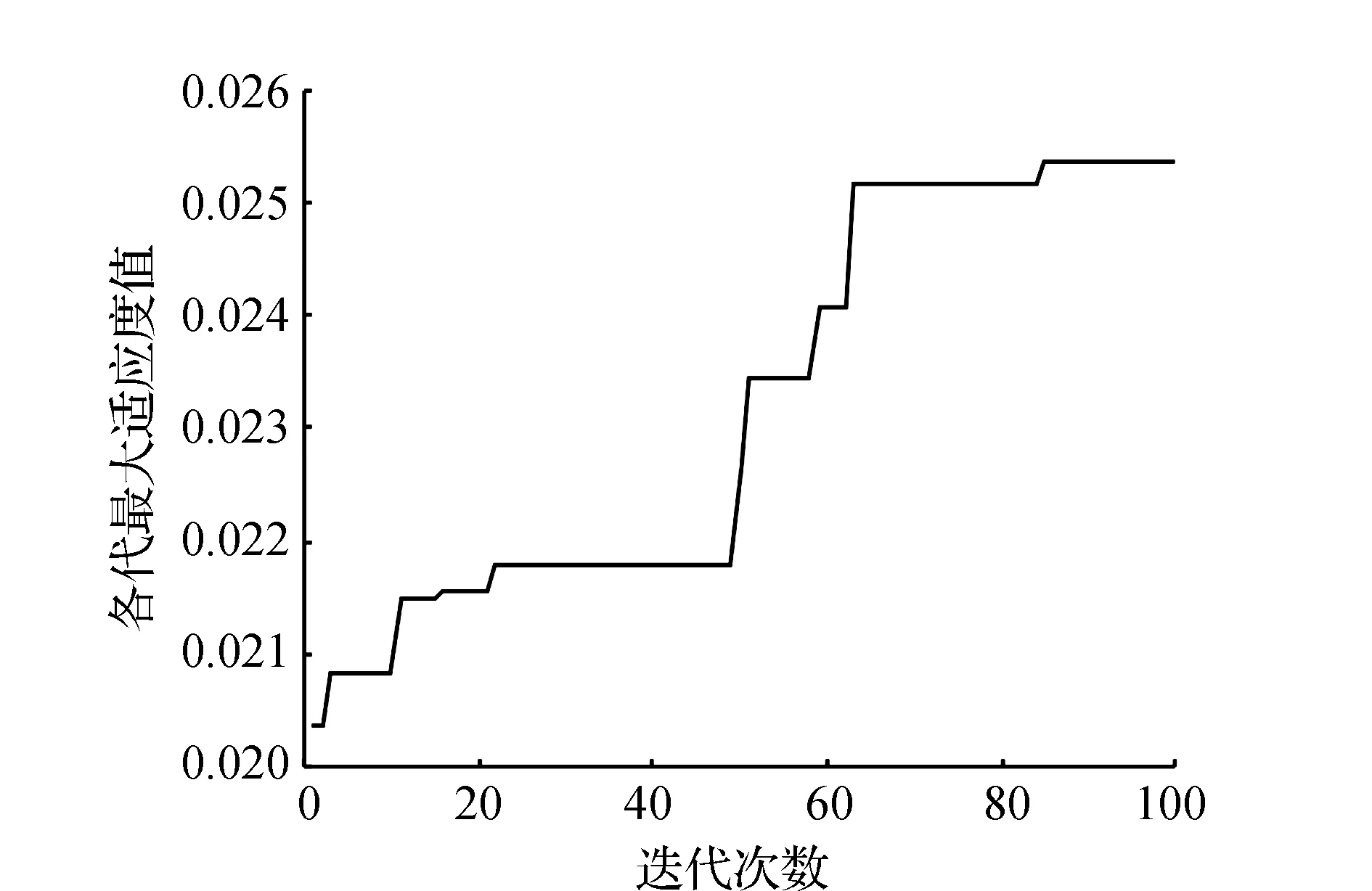
圖5 標準遺傳算法收斂曲線

通過對比分析兩種算法優化性能以及對所構建模型進行求解的最終結果，可以發現，標準遺傳算法在迭代85次后收斂，目標函數值為39.411 8。針對同樣問題，自適應遺傳算法達到穩定狀態只需迭代44次，目標函數值為31.282 4，結果表明自適應遺傳算法的尋優效果更好，效率更高。

4.2 結果分析

利用本文設計的自適應遺傳算法對不考慮零部件均衡重要程度的零部件消耗均衡化模型進行分析，即賦予每種零件相同的權重，可得到對應最優的混流裝配線排序方案為DABCAECDACEACABD。比較公司優化前的排序方案以及有無考慮零部件均衡重要程度兩種情況優化后的混流裝配線排序方案，可得到各零部件的消耗方差值，如表2所示。

由表2可見，相比公司現有的投產順序，無論采用哪種方式進行優化，都可大幅度降低各類零部件的消耗方差值，可見，使用零部件消耗均衡化模型確定的投產順序和零部件消耗均衡情況相較于公司現有的投產順序都會有較大的提升。另外，相比不考慮零部件均衡重要程度的情況，在考慮零部件均衡重要程度的情況下，p5和p6的消耗方差值分別由8.941 2降至6.117 6、12.588 2降至10.764 7，均衡效果分別提升31.578 9%和14.486%，p5,p6二者消耗方差之和由21.529 4降至16.882 3，重要零部件的總體均衡效果提升了21.584 7%。由此可知，基于零部件均衡重要程度的零部件消耗均衡化模型能夠優化混流裝配線的投產排序順序，并且可以對生產系統影響程度更為重要的零部件實現更好地均衡，從而優化生產系統，在生產制造過程中實現企業精益生產的目的。

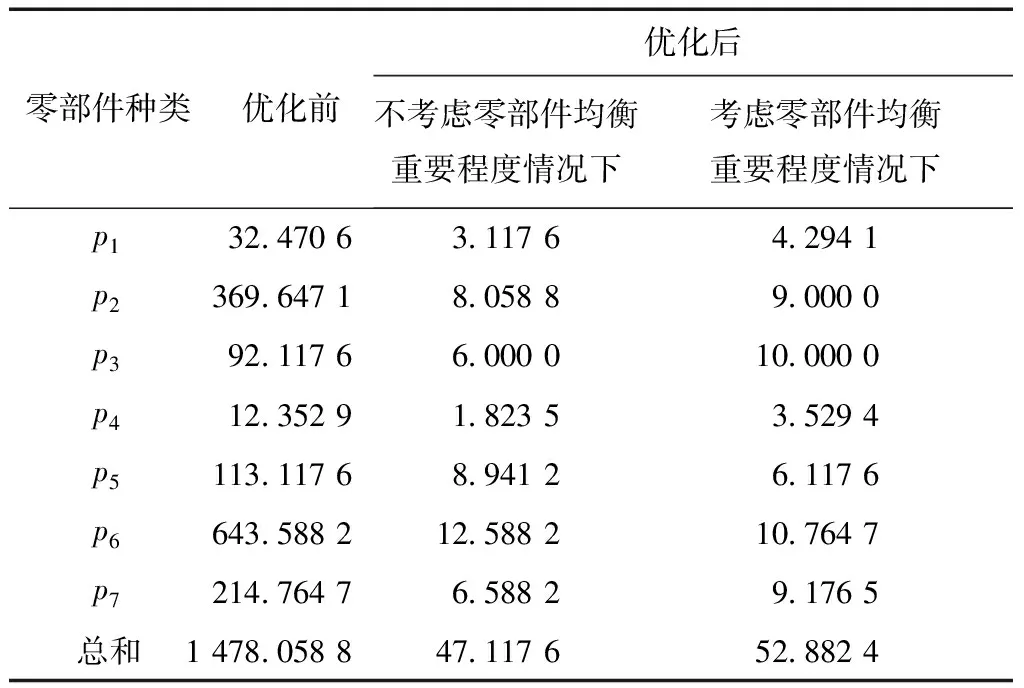
表2 不同排序方案下各零部件的消耗方差值

除此之外，為了最大限度地實現更為重要零件的均衡，造成各類零部件的總體消耗方差之和有所增加，由47.117 6增加至52.882 4。根據制造業的實際生產要求，以犧牲較小的總體消耗波動換取對生產系統影響更為重要的零部件最大限度地均衡是必要且可取的。

4.3 實驗分析

為了明確重要零部件消耗均衡與總體波動的關系，以確定對混流裝配線所需零部件總體的實質影響，本文根據不同情境設置不同的權重配比方案進行實驗分析，如表3所示。

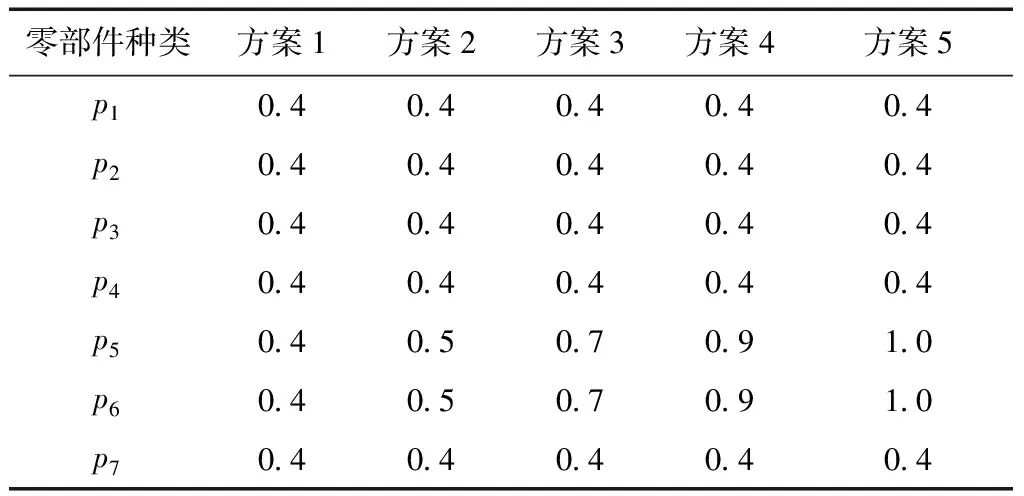
表3 不同的權重配比方案

方案1與方案5對應不考慮零部件均衡重要程度和考慮零部件均衡重要程度兩種情境下的解上文已求得，故只需對方案2、方案3和方案4的混流裝配線排序進行求解，得到對應的排產順序分別為DABCAECADACBADEAC、DABCAECADACBAEDCA、DABCAECADBADACECA。根據方案1～5的排產順序可得到對應的零部件總體消耗方差值分別為47.117 6、49.941 8、50.647 1、51.411 8、52.882 4，其中，重要零部件p5和p6的消耗方差之和分別為21.529 4、20.882 4、20.235 3、18.882 4、16.882 4。通過對方案1～5的總體零部件以及重要零部件消耗方差值進行分析，可以得到不同權重配比方案下各因素的變化曲線，如圖6所示。從圖中可以看出，自方案1至方案5，隨著重要零部件相對重要程度的增強，重要零部件消耗方差和逐漸減少，而總體消耗方差和逐漸增加。由此可以說明，重要零部件消耗均衡化與總體消耗均衡的目標相沖突，更好地均衡重要零部件的消耗是以增加生產系統總體消耗波動為代價的。因此，企業管理者在生產過程中應權衡考慮重要零部件的均衡與總體波動之間的關系，適時為企業管理提供合理決策。

圖6 不同權重配比方案下各因素的變化曲線

5 結束語

本文在傳統的零部件消耗均衡模型的基礎上進行改進，構建了基于零部件均衡重要程度的混流裝配線排序模型。根據所建模型，設計了自適應遺傳算法，并與標準遺傳算法進行對比，結果證明自適應遺傳算法的尋優效果更好，效率更高。通過案例的對比分析，證明在各類零部件的總體消耗波動不會顯著增加的情況下，基于零部件均衡重要程度的混流裝配線排序能夠對生產系統影響更大的零部件均衡情況有較大程度地改善。除此之外，通過對重要零部件配比不同的權重方案，證實重要零部件消耗均衡與總體波動之間的關系，對企業管理者合理決策具有借鑒意義。