基于Rasch模型的體育專業學生Excel考試質量分析

張國瑞 沈陽體育學院

計算機應用基礎課是各類高校均開設的一門重要的公共基礎課程，其教學內容包括計算機基礎知識、Word文字處理、Excel電子表格和PowerPoint演示文稿。結課后采用無紙化考試的方式對學生Word、Excel、PowerPoint等軟件的操作能力進行考核，本研究對其中的Excel考試試題質量進行分析，國內進行試題質量分析大多是在經典測試理論（classical testing theory，CCT）的基礎上進行分析，這種方法計算簡單但存在一些局限性，對抽樣質量要求過高、測量出的信度也存在一定的不準確[1]，也無法分析出學生的能力水平。而項目反應理論（item response theory，IRT）可以有效彌補CTT的不足。該理論中的Rasch模型目前應用也比較廣泛，這是一種利用數據擬合模型的分析方法，當數據擬合度差的時候可以根據模型需求對數據進行修改以便得到合理的模型，這個過程正好適合對考試試題做分析，不理想的試題可以根據模型理論進行修改[2]。因此本研究將Rasch模型引入到Excel考試的質量分析中，通過科學的定量分析，驗證試題的難易度以及學生的能力水平，為了日后修訂試題庫，提高試題質量提供理論依據。

一、研究對象與方法

（一）研究對象

本研究為了分析體育類專業學生Excel試題質量，隨機抽取體育教育、運動訓練、社會體育指導員等專業289名學生的Excel考試成績，學生考試過程采用計算機無紙化考試系統，全部試卷由系統自動判分，極大地避免了人為判卷中可能出現的誤差。本次考試Excel共有22道題，每題答對計1分，答錯計0分。

（二）研究方法

使用WINSTEPS 5.1.5.2軟件對所得數據進行Rasch分析，主要研究分析的內容為：總體擬合情況、單維度檢驗、題目與個體分析、懷特圖、氣泡圖等，通過上述分析研究試題質量并提出修改建議。

二、研究結果

（一）整體質量檢測

將考試數據導入Winsteps 5.1.5.2進行分析，試題的整體質量一般用擬合指數MNSQ（包括IMNSQ和OMNSQ）來表示。本次考試中學生和題目的擬合值數MNSQ（包括IMNSQ和OMNSQ）均接近理想值1，表明考試成績與Rasch模型的擬合度比較高。學生的分離度（PSI）為2.33，高于臨界值2，信度（PR）為0.84，高于臨界值0.8，綜合這兩個指標說明參與本次考試的學生樣本能力分布比較合理。試題的分離度（ISI）為5.69，高于臨界值2，信度（IR）為0.97，高于臨界值0.8，綜合這兩個指標說明試題的區分度比較理想。

（二）單維性檢驗

單維性是Rasch模型使用的前提條件之一，試題滿足單維性是指該試題考查學生某種單一能力或潛在特質。本研究利用Winsteps 5.1.5.2對殘差進行主成分分析（PCA），這樣可以將相關項目轉換為主成分，由此計算出來的解釋方差可以衡量模型的單維性，這里通常要求通過測量解釋的原始方差應大于50%，第一次對比未解釋的方差應小于3.0，本次考試成績殘差主成分分析結果，通過測量解釋的原始方差為58%，第一次對比未解釋的方差為2.76。說明本次考試數據滿足單維性的要求，適合做Rasch模型分析。

（三）各試題擬合度分析及誤差統計

應用Rasch模型分析實際數據時，還需要對該數據進行模型擬合度檢驗。該檢驗可以分析數據與模型的擬合情況，只有擬合情況符合要求時對實際數據進行Rasch分析才具有實際意義。Rasch擬合度分析中常用的指標是INFIT MNSQ和OUTFIT MNSQ，INFIT MNSQ是加權后的殘差均方，用來分析試題難度與所對應的學生能力水平是否相符。OUTFIT MNSQ是標準殘差的均方，用來分析異常數據。通常情況下這兩個MNSQ值介于0.5到1.5之間時，數據與模型的擬合程度可以接受，當該值為1時，數據與模型完全擬合。此外該值大于1.5時表示學生在答題時，作答方式與模型設定的方式不一致，即數據與模型不擬合[2]。該值小于0.5時，表示學生對某題的答題結果差異很小或者說這道題無法區分學生之間能力水平上的差異，即數據與模型過度擬合[1]。在對數據進行擬合度檢驗時可能出現INFIT MNSQ和OUTFIT MNSQ的結果不一致的情況，此時我們一般以INFIT MNSQ為準[1]。

本次考試各試題擬合度及誤差統計中題目Q1的INFIT MNSQ和OUTFIT MNSQ均大于1.5，說明該題目在測量學生與之相對應的能力時存在一些干擾因素。題目Q2的INFIT MNSQ和OUTFIT MNSQ均過小而無法測量，該題目回答的正確率為100%，無論能力水平高低，全部學生均答對了這道題，該題目區分度極差。其余題目INFIT MNSQ都在合理范圍內，數據擬合度良好。

（四）試題難度與學生能力水平分析

為了直觀的展示題目難度與學生能力、各題目難度、各學生能力之間的關系，本研究采用Rasch模型中的懷特圖，見圖1。懷特圖可以將Rasch模型中根據原始數據轉換成等距的logit值，將試題難度和學生能力放到同一量尺中進行標定，從而直接比較題目難度與學生能力、各題目難度、各學生能力之間的差異。

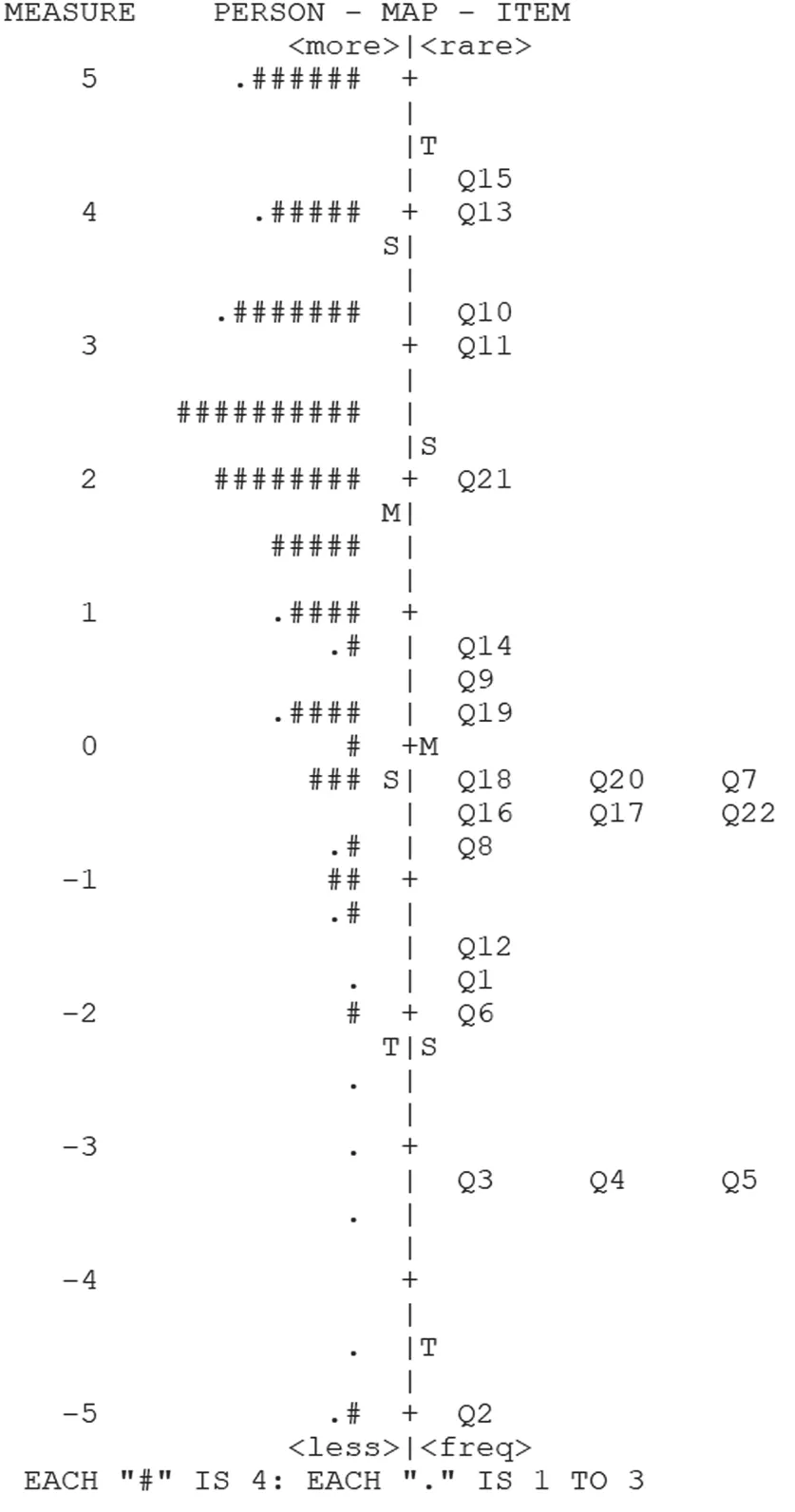
圖1 學生能力與試題難度關系懷特圖

圖1中，中線是logit刻度尺，中線左側表示學生的能力，中線右側表示試題的難度。圖中M表示平均水平，S是距離平均值一個標準差的距離，T是距離平均值兩個標準差的距離。刻度尺由上往下表示學生能力和試題難度的逐漸降低。中線左側的每一個“#”代表4名學生，每一個“.”代表1至3名學生。從圖1中可以看出本次考試學生能力的均值比試題難度均值高出將近2個logit的值，說明本次考試試題整體難度過低。其中，題目Q2、Q3、Q4、Q5難度都低于學生平均能力兩個標準差以上，對大部分學生而言這四道題沒有什么區分度。同時有25名以上的學生能力水平比難度最大的題目Q15的難度高了將近1個logit，說明對這一部分學生沒有能夠與之相匹配的題目。同樣在學生能力均值附近僅有1個題目Q21，在這一水平附近的學生人數最多，需要比較多的同等難度的題目來對學生進行測試，本次考試中僅有1道題顯然不夠。

三、結論與建議

本研究使用Rasch模型分析體育專業學生Excel考試的試題質量，通過分析可以認為Rasch可以很好地對本次考試進行分析。本次考試試題整體質量比較高，與Rasch模型擬合度比較高，整體區分度也比較理想，但是整體的難度比較低。本次考試Excel試題是從2018年建立的試題庫中隨機抽取的，試題難度是按當時學生的一般水平編寫的。2018年以來對體育類學生《計算機應用基礎》課進行了不斷地教學改革，從以教師為中心逐步轉變為以學生為中心，從單一的線下授課轉變為線上線下混合式的教學，在提升學生自主學習能力的同時也在不斷地提升學生對于Excel操作的水平。從本次考試的Rasch模型分析結果中可以看到，學生的能力水平已經高出試題難度將近2個logit，這個差距已經非常明顯的說明了學生能力有了顯著的提升。由此可見本課程Excel試題庫應該根據學生現有能力水平進行大范圍修訂。

此外，由于本次考試整體難度比較低，其余題目雖然在Rasch模型分析中未發現問題，為了提高試題整體難度，在試題修訂中也應在原題要求基礎上適當增加題目難度。與此同時，建議調整教學大綱，增加一些學習難度比較大的Excel操作知識。