含有對稱間隙的2自由度振動系統電路仿真

常逢亮，汪諍，胡國靜

（蘭州交通大學 機電工程學院，蘭州 730070）

非光滑機械系統具有復雜的動力學特性，其非線性特性由分段線性、間隙、干摩擦和時滯等非線性因素引起。對于含有間隙的分段線性機械振動系統，當振子在間歇內運動時為線性系統，而一旦接觸到邊界時，系統將出現彈性系數的突變，造成強烈的振動和噪聲，促使機械零件加速磨損和沖擊，引起的隨機性載荷嚴重影響到機械零件的壽命和可靠性[1-2]。

非線性機械振動的研究是近年來研究的熱點，其以理論研究和數值仿真為手段進行分析。數值仿真采用MATLAB、Fortran或C等編程語言實現，通過長時間的計算獲得分岔圖和相圖。由于數值仿真應用了數值迭代求解微分和積分方程，當精度要求很高時，計算需要花費漫長的時間和巨大的計算量[3]。為了能夠快速完成計算過程，研究者通常對算法進行優化，提高數值計算的效率，或采用昂貴的高性能計算機，以期縮短計算時長。

本論文建立了2自由度線性系統的傳遞函數，確定了非線性特征發生的頻率范圍。以Multisim為仿真軟件，設計了與數學模型完全等效的電子電路模型，該等效電路模型僅由幾個TL074CN運算放大器和電阻電容組成，通過仿真得到非線性動力學中相圖，不僅極大地降低了對于算法和編程能力的要求，而且電路圖具有能直觀表達方程式的優點，同時Multisim具有運行時間短和調整參數簡便的優點。

1 對稱間隙的2自由度振動系統模型

1.1 動力學模型和數值仿真

典型的含有對稱間隙2自由度振動系統的動力學模型如圖1所示，質量M2通過線性彈簧K2和線性阻尼C2與機架連接，并且在簡諧激勵P2sin(ωt+τ)的作用下運動。質量M1通過線性彈簧K1和線性阻尼C1與質量M2連接，在距離質量M1零點（M1和M2在受力為0的平衡點）B的兩端有線性彈簧K0。設在靜態情況下M1和M2所在位置為x1和x2。當質量M1的位移小于對稱間隙B時，M1和M2為一個2自由度線性振動系統，當質量M1的位移大于+B或-B時，其與線性彈簧K0接觸并發生作用，此時M1受到分段線性彈簧力的作用，并且產生非線性運動。

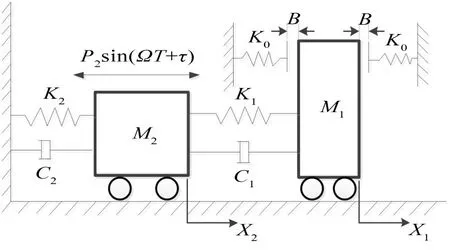
圖1 動力學模型

根據動力學理論，可以建立質量M1和M2的物理方程：

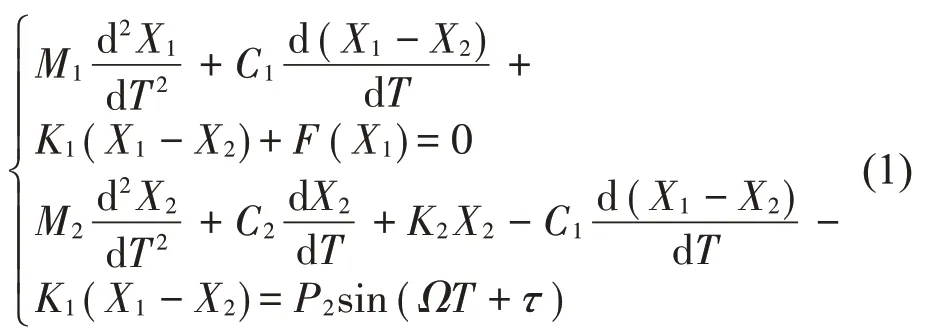
式中非線性部分為

式(1)為物理方程，其每個因子均含有量綱，為了分析方便，將式(1)轉換為無量綱方程，取無量綱化參數為

則可得到方程的無量綱化形式，即數學方程為

非線性部分為

式(2)中的系數有5個，隨著變量ω的變化，系統的運動特性將呈現復雜的運動特征。選取μm=μc=μk1=1，μk0=25，ζ=0.2，δ=0.2，首先確定質量M1與線性彈簧K0不發生接觸的頻率范圍。此時，系統為一個線性系統，將式(2)中的非線性項去掉，即可得到線性方程為

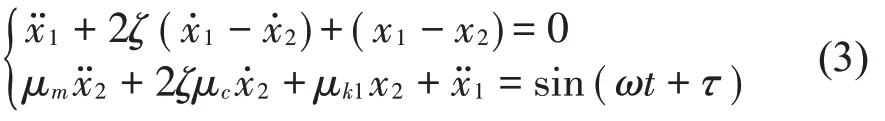
根據動力學模型，對于質量M1，輸入可以認為是X2，輸出為X1；對于質量M2，輸入為激勵信號sin(ωt+τ)，輸出為X2；而整個系統的輸入為激勵信號sin(ωt+τ)，輸出為X1，建立式(3)的第一個方程的傳遞函數，有：

則：

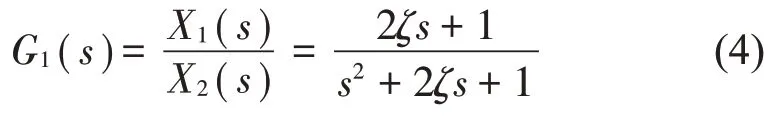
建立式(3)的第二個方程的傳遞函數，有：

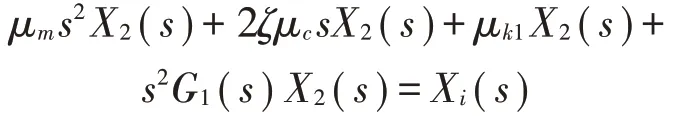
則：

以系統激勵信號為輸入信號，輸出為X1(s)，則系統的傳遞函數為

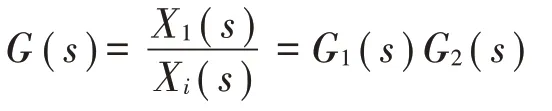
則：

將μm=μc=μk1=1,μk0=25,ζ=0.2,δ=0.2代入式(6)中可以得到：

在Simulink中繪制系統的伯德圖，如圖2所示。可以看出，系統在頻率為1.9附近增益為0.2（縱坐標最小值設為0.2），隨后繼續下降，因此，系統只有在頻率低于1.9時才可能與線性彈簧K0發生接觸碰撞。圖中橫坐標為頻率，縱坐標為增益。

1.2 分岔圖和相圖

根據上述分析，并根據圖2和式(7)，可知當μm=μc=μk1=1,μk0=25,ζ=0.2,δ=0.2時，系統中質量M1僅在激振頻率小于1.9時才會與線性彈簧K0發生接觸并碰撞，系統進入非線性運行范圍，而在頻率高于1.9時，系統整體呈現線性狀態。將參數代入式(2)，令對方程進行狀態轉換，轉換為1階微分方程，即狀態方程為

圖2 伯德圖

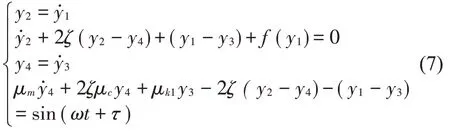
式(7)中非線性部分f(y1)為

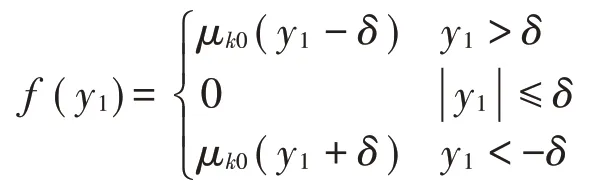
根據狀態方程式(7)，經過編程繪制分岔圖，如圖3所示。圖中橫坐標為頻率ω，縱坐標均為相對速度y2-y4。

從分岔圖3中可以看出，隨著頻率ω的變化，含有間隙的2自由度振動系統隨著激勵頻率的變化，系統出現了單周期、2周期、4周期和混沌等復雜的非線性運動特征。根據分岔圖，選取圖3中的1.35、1.395、1.4、1.44，如圖4所示。圖中橫坐標為M1相對M2的位移y1-y3，縱坐標為M1相對M2的速度y2-y4。

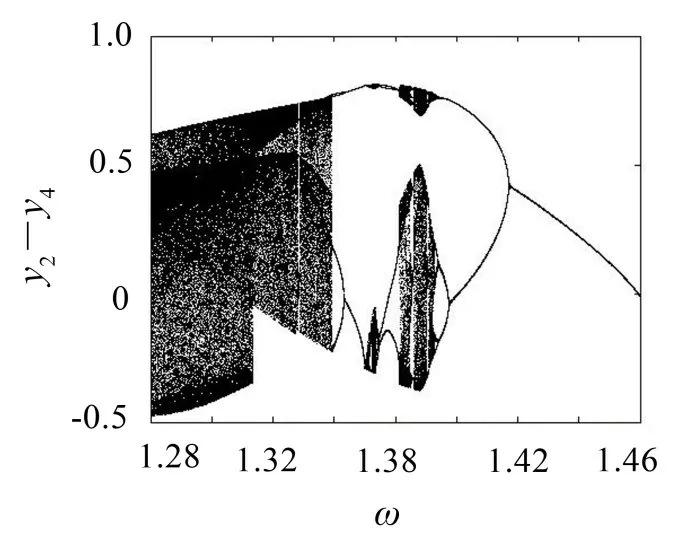
圖3 分岔圖

2 電路仿真

使用等效電路實現振動系統的分析，首先要將振動系統的方程轉換成等效的電路方程[4-7]，將式（7）轉換為積分形式：

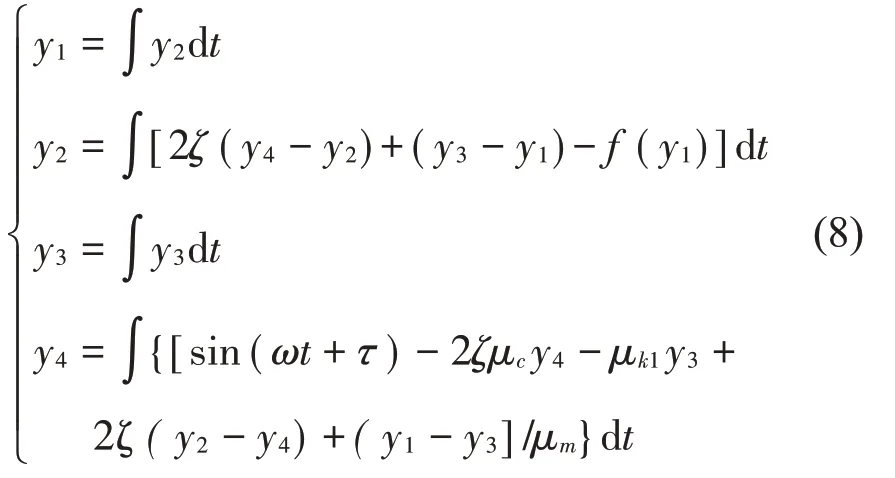
圖4 相圖

非線性部分為

在此選擇有源積分電路，將式（8）轉換成等效的電路方程即：

非線性部分為

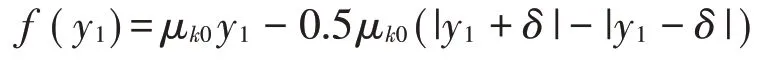
分別選用4個積分模塊來實現式(9)，其中運算放大器選用TL074CN，電路設計圖如圖5所示。其中第一個方程由U1A和U1B實現；第二個方程由U2C、U4B和U4C組成；第三個方程由U1C和U1D組成；第四個方程由U3A、U3B、U3C組成，U4A和U2A為反相器，非線性函數由軟件提供的NONLINEAR-DEPENDENT模塊實現，供電電壓選擇±18 V，將式（9）轉換為2階微分方程[8-9]，則有：

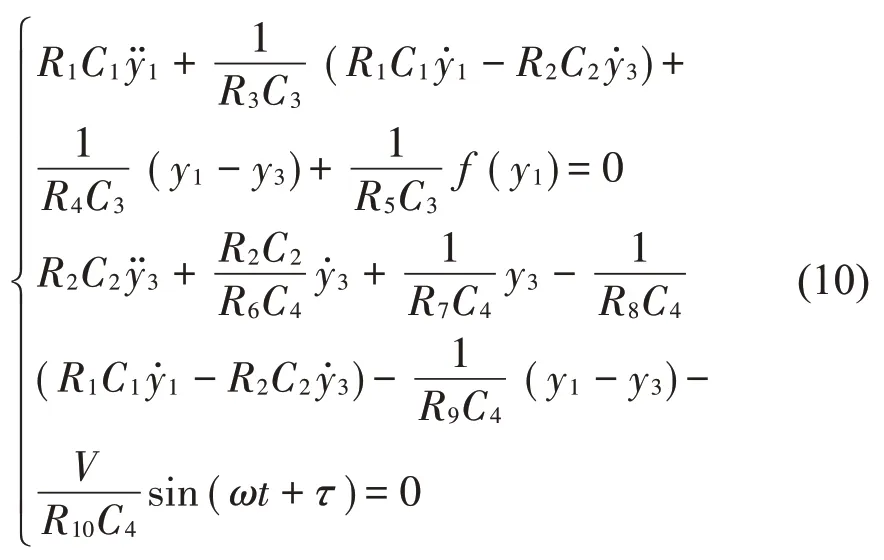
式(10)和式(1)形式上完全相同，為了使兩式實現等效，必須確定式(10)中各個參數的數值。根據無量綱化過程選取的參數，即μm=μc=μk1=1，μk0=25，ζ=0.2，δ=0.2.考慮到電阻電容的影響，選取R1=R2=10 kΩ，R10=100 kΩ，C1=C2=C3=C4=22 nf，則得到R4=R7=30 kΩ，R5=R9=30 kΩ，R3=R6=R8=43.3 kΩ，其余電阻僅用于反相電路，所以均取100 kΩ。

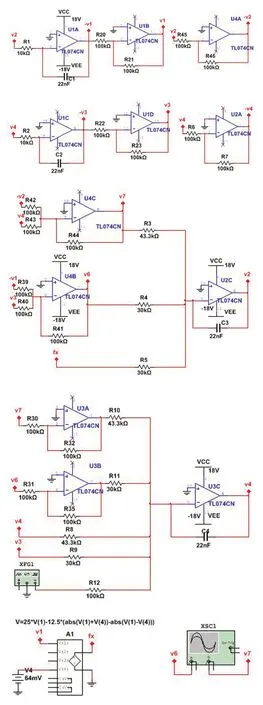
圖5 電路圖

正弦波函數的幅值可由δ=0.2求得：

δ=0.2，即可得Vm=1.067 V

由無量綱化過程，可得出激勵頻率f和ω之間的關系為

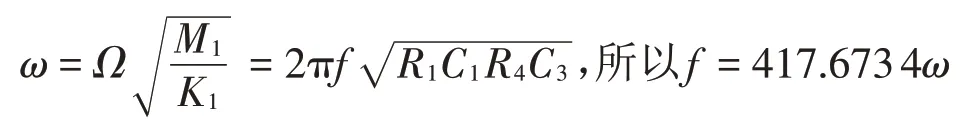
3 Multisim12.0仿真

通過MultiSim12.0對電路模型進行仿真，函數發生器正弦波幅值為1.067 V，選擇激勵頻率分別為563.86 Hz(1.35ω)、582.65 Hz(1.395ω)、584.74 Hz(1.4ω)、601.45 Hz(1.44ω)，運行結果如圖6所示。示波器中橫坐標通道1為位移(y1-y3)，刻度為100 mV/Div；縱坐標通道2為速度(y2-y4)，刻度為100 mV/Div。

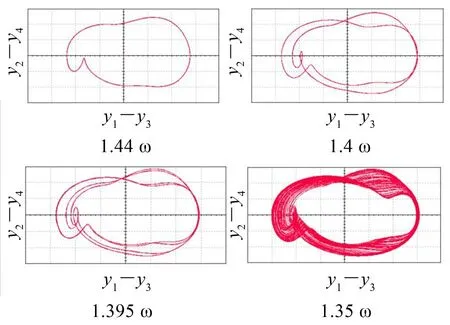
圖6 電路仿真相圖

相比較于通過編程繪制相圖，Multisim12.0繪制的相圖和其完全一樣。自行編程的運行時間為等效電路仿真的3倍，說明了程序需要進行更進一步的優化，當然更說明了編程對于非線性研究的影響太大，能降低其影響，可以提高研究效率。同時電路仿真還擁有著動態參數可調的優點，利用等效電路分析非線性動力學，降低對編程要求，提高研究的效率。

4 結語

通過對2自由度線性系統建立傳遞函數，應用bode圖分析分段線性系統的碰撞區間，確定分段線性動力學系統發生非線性特性的頻率范圍，減少數值分析的計算時長。應用Multisim12.0電路仿真軟件中的NONLINEAR-DEPENDENT模塊及幾個TL074CN運算放大器、電阻電容等簡單的電路元器件，快速建立與動力學模型等效的電路模型，得到與數值仿真相同的結果。由此可見等效電路可以實現非線性動力學的分析和研究，節省了數值仿真對算法、編程和計算機性能的要求，為非線性動力學研究提供了一種很好的研究方法。