結構參數對地鐵引起建筑結構噪聲影響分析

劉長卿

（上海市環境科學研究院 上海城市環境噪聲控制工程技術研究中心，上海 200233）

城市軌道交通以其快速、便捷、節能等優勢在大型城市交通網中的作用越來越突出。伴隨著城市軌道交通的大力發展，其運行引起的環境振動及二次結構噪聲擾民問題也來越受到人們的關注。對于上海、北京、廣州等特大城市，地鐵下穿居民區的情況十分普遍，地鐵引起的振動可直接傳遞至建筑內引發樓板振動，同時，振動引起的二次結構噪聲也給人們的生活帶來影響。近年來，國內外研究人員針對地鐵引起的振動及結構噪聲問題做了大量研究工作。辜小安等[1]對我國城市軌道交通列車運行引起的建筑物二次輻射噪聲的預測和參考標準的適宜性進行了探討。Zou等[2]針對地鐵車輛段不同位置引起的建筑振動和二次結構噪聲進行了測試分析，對新建地鐵車輛段的規劃設計提出了建議。鄔玉斌等[3]以地鐵鄰近音樂排練廳為例，對建筑室內振動和二次結構噪聲進行了實測與數值仿真，得到了地鐵引起的建筑室內結構噪聲影響規律并驗證了數值計算的可靠性。陳俊杰[4]提出了地鐵列車振動影響下建筑結構二次輻射噪聲預測方法，并選取北京某鄰近地鐵建筑進行結構噪聲實測，對該預測方法進行了驗證。Mouzakis等[5]利用實測傳遞函數法對地鐵引起的住宅建筑內振動及結構噪聲進行了評估，并提出了控制建議。楊尚福[6]通過仿真計算研究了軟土層、硬土層和硬質巖層3種土體條件下地鐵引起的建筑振動及結構噪聲影響。張宇明等[7]以某營運中的地下雙層地鐵停車場為研究對象，通過實測法及數值分析法研究了地鐵上蓋建筑地鐵振動及二次結構噪聲影響。我國國家環保部發布的2008版和2018版的《環境影響評價技術導則城市軌道交通》（HJ 453）中均給出了軌道交通引起的建筑結構噪聲預測公式。

以往研究成果以結構噪聲的預測方法研究為主，未涉及到對影響結構噪聲的結構材料參數分析。本文基于以往的研究方法及成果，選取上海某地鐵線路及其上蓋鄰近建筑為研究對象，采用半實測半數值的振動分析方法以及經驗公式法計算地鐵引起的鄰近建筑室內結構噪聲，分析建筑結構噪聲對混凝土和土層彈性模量、阻尼系數等參數的敏感性，為城市軌道交通引起的建筑室內二次結構噪聲降噪設計提供參考。

1 結構噪聲計算方法概述

針對地鐵引起的建筑室內結構噪聲問題，首先采用半實測半數值的振動分析方法，計算得到建筑室內結構的振動響應，即建筑室內樓板垂向振動加速度級（計算方法詳見文獻[8-9]），然后根據樓板振動預測結果，利用理論公式法，對結構噪聲進行預測。

基于Kurzweil模型[10]，被振動激勵的建筑物表面輻射的聲功率為

式中：W為建筑結構振動激發的聲功率，Z0=ρ0c0為空氣特性阻抗，σ為聲輻射效率。S為室內地板的面積，v為地板表面振動速度。

考慮了直達聲和混響聲兩部分，室內聲壓可表示為

式中：r是地面到測量點的距離，R為房間常數，與房間內平均吸聲系數和房間總表面積有關。

房間內結構輻射聲的聲壓級Lp可表示為

將式（2）代入式（3），得到：

式中：Lv為振動速度級，C為常數，表達式為

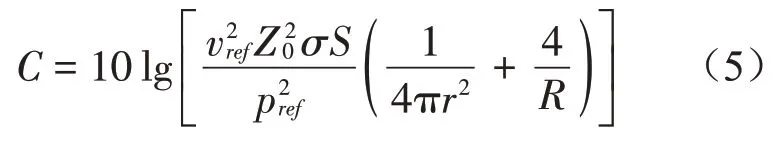
地鐵振動近似假設為簡諧振動，則單頻結構噪聲聲壓級Lp,f可表示為振動加速度級的函數：

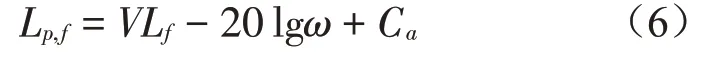
Ca為常數，表達式為

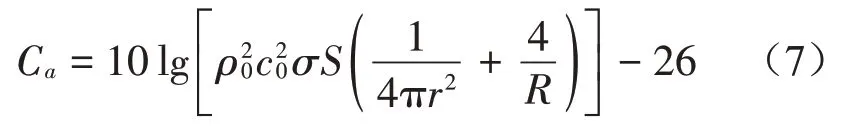
式中：VLf為振動加速度級頻率響應，ω為簡諧振動圓頻率。

綜上，當房間常數R及房間尺寸參數確定時可得到Ca值，在利用半實測半數值的振動分析方法得到室內樓板各頻率振動加速度級VLf的情況下，通過式（6）即可求出各頻率對應的結構噪聲聲壓級Lp,f。

2 數值模型及結構材料參數設定

本文選取的待分析建筑為地鐵鄰近上蓋住宅建筑，其中地上部分共13層，高度約40 m，地下部分為2層的車庫和設備間，深度約10 m。地鐵線路從建筑側下方穿過，其站臺上方緊鄰住宅地下室，地鐵位于地下5層，埋深約30 m。地鐵線路與建筑相對位置示意圖如圖1所示。

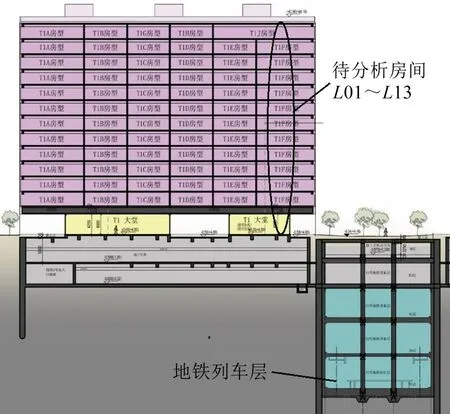
圖1 地鐵線路與建筑位置示意圖

根據該建筑與地鐵工程設計圖，建立三維有限元模型。為減小土層邊界反射波影響，模型邊界采用黏彈性人工邊界。激振力載荷施加在站臺軌道道床處，沿行車線施加多點激勵單位載荷，計算靠近地鐵站臺一側L01～L13樓層房間的結構噪聲（結構模型如圖2）。

圖2 三維有限元結構模型

鋼筋混凝土結構材料參數按實際結構設計的混凝土等級設定，如表1所示。土層類型根據該地塊地質勘查報告及《建筑抗震設計規范》（GB50011－2010）[11]進行簡化，等效參數見表2，其中ρ為土層密度，μ為泊松比，E為動彈性模量。上述材料參數在計算中均作為設計值輸入模型。

表1 混凝土等效參數

表2 土層等效參數

3 振動源強

地鐵運行過程中，列車與輪軌間的相互作用引起道床振動，并經由隧道結構傳遞到土層以及鄰近建筑中。軌道道床作為振動的源頭，其振動特性及振動強度對于環境振動的預測至關重要。由于待分析地鐵線路已開通運行，為了準確獲取振動源強，對待分析地鐵線路進行了道床振動源強測試。道床測試點位照片如圖3所示。測試過程中，采用IEPE型加速度傳感器KD1050L以及德國HEIM DATaRec 4 Series 24通道數據采集儀連續采集10組列車經過時的道床垂向振動加速度數據，列車車型為A型車。

圖3 道床振動源強測點照片

由于篇幅限制，僅展示某一次列車經過時的道床振動加速度時程曲線，如圖4所示。將10組列車經過時道床鉛垂向振動加速度進行平均處理，得到加速度級1/3倍頻程頻譜如圖5所示。利用該源強頻譜結合有限元模型可計算建筑樓板鉛垂向振動加速度級。

圖4 某列車經過時道床鉛垂向振動加速度時程曲線

圖5 道床振動源強加速度級頻譜10列車平均值

4 室內振動及結構噪聲分析

4.1 各樓層振動及結構噪聲計算結果

根據實測振動源強頻譜，利用半實測半數值的振動分析方法，可求解建筑室內樓板垂向振動加速度級。根據《城市軌道交通引起建筑物振動與二次輻射噪聲限值及其測量方法標準》[12]，地鐵引起的建筑結構二次輻射噪聲主要頻段為16 Hz～200 Hz，故本文對樓板振動僅計算16 Hz～200 Hz頻段內振動加速度級，對結構噪聲僅計算16 Hz～200 Hz頻段內總的A計權聲壓級。

對本文待分析房間結構噪聲的預測，取空氣密度ρ0=1.29 kg/m3，聲速c0=340 m/s，聲輻射效率σ≈1，室內地板的面積S=10 m2，房間高度為2.8 m，混響時間為0.8 s的一般裝修房間常數R=5.64，代入式（7）可求得地面上r=1.2 m處的Ca值為35.7，將半實測半數值法求解的建筑室內樓板不同頻率的鉛垂向振動加速度級代入結構噪聲預測公式（6），可計算得到不同頻率的室內結構噪聲值Lp,f，利用A計權網絡對其1/3倍頻帶中心頻率聲壓級計權后進行能量疊加，可求出待分析頻段內總的A計權聲壓級。

各樓層靠近地鐵一側的房間樓板垂向振動及結構噪聲預測結果如圖6至圖7所示。結果表明：

圖6 樓板振動及結構噪聲隨樓層變化對比曲線

圖7 部分樓層結構噪聲頻譜對比

（1）結構噪聲A聲級隨樓層升高整體呈減小趨勢，但部分樓層有回彈放大現象；

（2）樓板垂向振動與結構噪聲呈現正相關，兩者隨樓層升高變化趨勢一致；

（3）結構噪聲影響較大的1、4、13樓房間結構噪聲1/3倍頻程頻譜曲線對比可見，隨著樓層升高，40 Hz以上較高頻段結構噪聲迅速衰減，40 Hz以下較低頻段噪聲略有放大。

4.2 結構參數對室內結構噪聲影響分析

分別將結構模型中混凝土和土層的彈性模量E和阻尼系數ξ按表1、表2原始設計值±20%浮動取值計算室內結構噪聲，并與原始設計值對應的結構噪聲計算結果對比，分析上述參數對室內結構噪聲的影響。

各樓層靠近地鐵一側的房間結構噪聲對材料參數敏感性分析結果如圖8至圖11所示。結果表明：

圖8 混凝土彈性模量對結構噪聲影響

（1）結構噪聲對混凝土彈性模量敏感性最強。在混凝土彈性模量設計值±20%浮動條件下，結構噪聲對混凝土的彈性模量敏感性最強，建筑室內A聲級出現最大8.2 dB的波動，變化比例最大為38.9%；

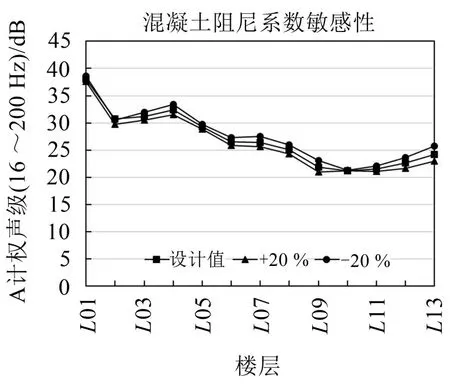
圖9 混凝土阻尼系數對結構噪聲影響

圖10 土彈性模量對結構噪聲影響

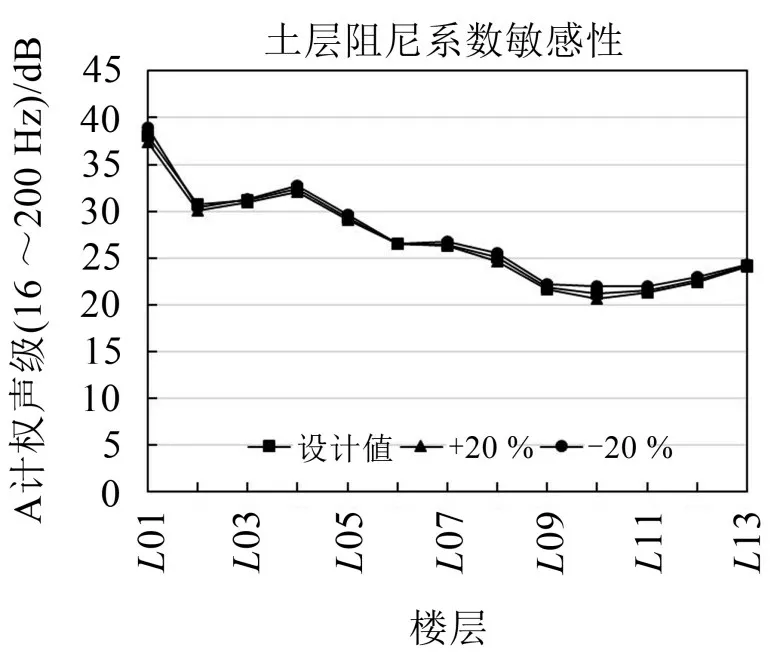
圖11 土阻尼系數對結構噪聲影響

（2）結構噪聲對土層彈性模量敏感性次于混凝土彈性模量，在土層彈性模量設計值±20%浮動條件下，室內A聲級最大3.8 dB的波動，變化比例最大為17%；

（3）結構噪聲對混凝土阻尼系數敏感性較低，在混凝土阻尼系數設計值±20%浮動條件下，室內A聲級最大波動1.7 dB，變化比例最大為6.3%；

（4）結構噪聲對混凝土阻尼系數敏感性最低，在土層阻尼系數設計值±20%浮動條件下，室內A聲級最大波動0.8 dB，變化比例最大為3.9%。

5 結語

本文利用半實測半數值的振動分析法和經驗公式法對地鐵引起的建筑室內二次結構噪聲進行了計算，分析了混凝土和土層彈性模量、阻尼系數等參數在原始設計值基礎上±20%變化幅度的情況下對建筑室內結構噪聲的影響，得出以下結論：

（1）結構噪聲A聲級隨樓層升高整體呈減小趨勢，但部分樓層有回彈放大現象。樓板垂向振動與結構噪聲隨樓層升高變化趨勢一致。隨著樓層升高，40 Hz以上較高頻段結構噪聲迅速衰減，40 Hz以下較低頻段噪聲略有放大；

（2）在單項參數±20%浮動條件下，結構噪聲對混凝土的彈性模量敏感性最強，建筑室內A聲級出現最大8.2 dB的波動，變化比例最大為38.9%；對土層彈性模量敏感性次之，A聲級最大3.8 dB的波動，變化比例最大為17%；對混凝土和土層的阻尼系數敏感性均較低，A聲級最大波動不超過2 dB，A聲級變化均在7%以內；

（3）地鐵鄰近建筑減振降噪設計中，由于混凝土彈性模量對結構噪聲影響最大，在保證結構安全性的前提下，應選定合理的混凝土強度等級，以確保其彈性模量有利于降低室內結構噪聲的影響。