多孔夾芯層組合方式對夾層板隔聲特性影響研究

魏斌，張冠軍,2，陳足君，胡方濤

（1.武漢理工大學 能源與動力工程學院，武漢 430063；2.武漢理工大學 高性能船舶技術教育部重點實驗室，武漢 430063；3．中國人民解放軍第四八一二工廠，安徽 安慶 246001）

船用設備功率的增加以及相關法規的修訂對船舶減振降噪提出了更加嚴格的要求。

現代船舶噪聲控制的主要隔聲結構為復合材料夾層板，這種結構具有重量輕、隔聲量高的優點。彈性多孔材料密度小、吸聲性能好而且還具有一定的阻尼作用，將其應用到夾層結構中一是有利于改善結構的隔聲性能，二是有利于結構的輕量化，三是有利于在空間有限的下情況下保持結構厚度不變，如隔聲罩，利用現有材料構造不同的夾層結構可減少研發新材料的成本。因此，開展彈性多孔吸聲夾芯層合板的隔聲特性研究具有重要的工程應用價值。

穿孔板、阻尼層以及鋼板結構參數對隔聲特性影響的研究已較多，且有成熟的理論支撐。而多孔吸聲夾芯層由于其種類和結構的多樣性，對結構隔聲特性的影響規律也不盡相同。寧少武等[1]采用等效流體模擬吸聲材料，分析了聲波入射角和方位角、流場流速和流向、夾層結構幾何尺寸等參數對填充吸聲材料夾層板結構聲振耦合特性的影響。Xin等[2]采用等效流體模型分別研究了填充吸聲材料夾層板結構的聲輻射和聲透射特性，分析了填充吸聲材料對正交加筋板結構聲輻射和聲透射的影響。陳衛松和邱小軍[3]應用Biot理論，采用傳遞矩陣法推導了三層夾芯板的隔聲量計算公式，指出了夾芯板在中高頻段的隔聲優勢以及板結構對隔聲性能的影響。白聰等[4]應用Biot理論分析了聲波隨機入射時結構布局不同的三聚氰胺芯層復合板結構的隔聲特性，結果表明在中高頻率范圍內，三聚氰胺泡沫復合板結構的隔聲量遠高于聚氨酯芯層復合板結構。Panneton等[5]采用有限元法和邊界元法研究了層芯為不同彈性多孔材料的夾層板的聲透射問題，結果表明多孔彈性材料能夠顯著增加結構的阻尼，且阻尼的大小與材料屬性和結構的設計有關。楊永鉀等[6]采用VA One軟件分析了多孔吸聲夾芯層層數、材料厚度、密度對船舶艙室隔聲性能的影響，研究結果表明針對不同工況的艙室采用不同的多孔吸聲材料可以提高船舶整體的降噪水平。

自動匹配層技術（Automatic matched layer,AML）是在完美匹配層技術（Perfect matched layer，PML）基礎上發展而來一種求解聲場輻射問題的方法，解決了PML方法中因手動定義匹配層屬性對計算結果精度的影響，提高了求解精度和計算效率。直接聲振耦合方法是指同時建立結構模型和聲學模型，對聲振耦合問題統一求解。在Virtual Lab Acoustics軟件中可以通過定義AML表面，利用軟件中集成的結構求解器，可以快速實現基于有限元和自動匹配層（FEM-AML）技術的直接聲振耦合計算方法。

不同種類的多孔吸聲夾芯層材料、夾芯層結構及參數對結構隔聲性能的影響研究已較多，但對于不同種類夾芯層組合后對結構隔聲特性影響的分析較少。本文依據多孔材料的等效流體模型和穿孔板等效為多孔材料的理論[7]，建立了由微穿孔板，吸聲材料，阻尼層和鋼板組成的夾層板模型，采用FEMAML直接聲振耦合計算方法研究了兩種多孔吸聲材料組合排列方式對結構隔聲特性的影響。

1 彈性多孔材料與穿孔板的聲學模型

聲波在媒質中傳播時聲能減少或被轉化為其他形式能量的現象稱為吸聲，多孔材料由表及里具有大量的相互貫通的微孔，通過黏滯損耗和熱傳導損耗實現對聲能的吸收。假設有一無限大的平面剛性物體在均勻媒質中沿著法線方向來回振動，由振動引起的平面波聲壓p和質點振動速度vx可表示為[8]（假設沿x方向運動）

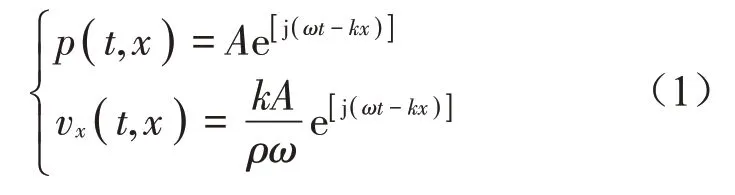
式中：A表示聲壓幅值，ω=2πf為角頻率，k=表示波數,ρ表示媒質密度，K表示媒質的體積彈性模量。由平面波的性質可知，其聲壓和質點振動速度之間的關系可以用媒質的特性阻抗Z來表示，即：

因此只要知道媒質的體積彈性模型和密度或者媒質的特性阻抗和波數，便可對多孔材料中的聲場進行求解。可以使用經驗模型或者等效流體模型求解多孔材料聲學參數，本文使用Johnson-Chanpoux-Allard等效流體模型，多孔材料的等效密度ρ和體積彈性模量K的表達式為[9]

式中：α∞表示曲折因子，ρ0為空氣密度，σ表示多孔材料流阻率，φ表示孔隙率，ω表示角頻率，η表示空氣的動力粘度，Λ表示材料粘性特征長度，γ表示空氣比熱比，P0表示標準大氣壓，Λ′表示熱效特征長度，B表示普朗克常數。

穿孔板雖然幾何結構簡單，但是其有限元模型往往比較復雜不適合直接進行有限元建模與仿真。研究表明微穿孔板的吸聲機理與多孔材料理論之間存在微妙的關系，可將微穿孔板視為薄的多孔材料進行模擬。兩種模型的參數轉化如下：

式(4)中：Φ孔隙率；p穿孔率；σ流阻率；η空氣動力黏度；r孔半徑；δ特征黏性長度；δ'特征熱效長度；a∞曲折因子；t板厚；Re(αp)，為所附吸聲材料動態曲折系數實數部分。圓孔正方形排列時：

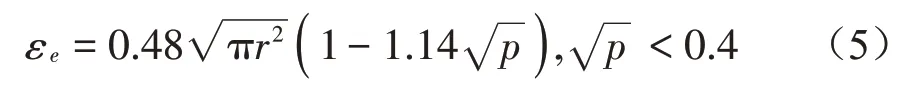
正方形孔正方形排列時：

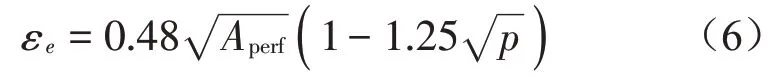
當0≤p≤1時：

2 夾芯層對結構隔聲特性的影響分析

在Virtural.Lab Acoustics軟件中使用Johnson-Chanpoux-Allard模型定義彈性多孔材料屬性，材料屬性定義包括流體屬性，幾何屬性和彈性屬性。流體屬性即孔隙之間的流體屬性，默認為空氣；幾何屬性包括靜態流阻率、孔隙率、曲折因子、特征黏性長度和特征熱效長度；彈性屬性包括楊氏模量、泊松比和體積密度[10]。

2.1 仿真計算方法驗證

為驗證本文仿真計算方法的準確性，在與文獻[11]中參數相同的情況下，采用FEM-AML直接聲振耦合方法模擬阻抗管結構計算了多層板結構的隔聲量，并與其實驗結果進行了對比，計算頻率為100 Hz到3 000 Hz的1/3倍頻程頻率點，仿真模型[12-13]和計算結果如圖1和圖2所示。

圖1 仿真計算模型

由圖2可知仿真結果與文獻實驗數據吻合較好，表明本文采用的FEM-AML直接聲振耦合方法計算多層結構的隔聲量是合理準確的。

圖2 仿真值與文獻實驗數據對比

2.2 夾芯層種類的影響

夾層板基本結構如圖3所示。尺寸為1 200 mm×1 000 mm×50 mm，從上到下依次分為微穿孔板、夾芯層、阻尼層和鋼板，原始模型參數為：鋼板厚度2 mm，密度7 850 kg/m3，楊氏模量2×1011Pa，泊松比0.3；阻尼層厚度1 mm，密度320 kg/m3，楊氏模量3×108Pa，泊松比0.25；夾芯材料厚度45 mm，流體默認為空氣屬性；穿孔板厚度2 mm，穿孔直徑0.5 mm，穿孔率0.5 %，材質為聚四氟乙烯，密度2 100 kg/m3，楊氏模量5×108Pa，泊松比0.4。建立幾何模型并完成網格劃分，空氣網格尺寸為50 mm，結構網格尺寸在長度和寬度方向上為50 mm，在厚度方向上吸聲材料網格尺寸為5 mm，鋼板網格尺寸2 mm，穿孔板網格尺寸2 mm，阻尼層網格尺寸1 mm。在Virtural.Lab Acoustic軟件中利用“Trap”功能和網格布爾運算完成夾層板結構每一層的劃分，使用自由邊界條件，采用FEM-AML直接聲振耦合方法模擬混響室計算夾層結構的隔聲量，計算頻率20 Hz到1 000 Hz，步長10 Hz，仿真模型[14]如圖4所示。

圖3 夾層板基本結構示意圖

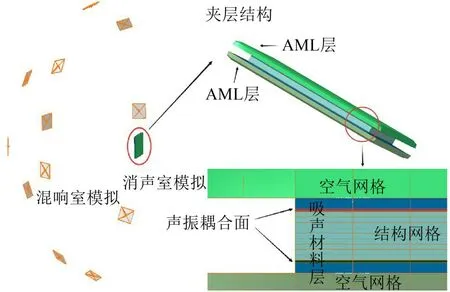
圖4 混響室法仿真模型

保持原始模型參數不變，考慮不同夾芯材料[15]對結構隔聲性能的影響。材料1：靜態流阻22 000 Pa·s/m2，孔隙率0.97，曲折因子1.38，特征黏性長度1.7×10-5m，特征熱效長度4×10-5m，彈性模量192 00+24 960 i Pa，泊松比0.23，體積密度827 kg/m3；材料2：靜態流阻75 000 Pa·s/m2，孔隙率0.95，曲折因子1.1，特征黏性長度4.4×10-5m，特征熱效長度6.3×10-5m，彈性模量333 300+33 330 i Pa，泊松比0.3，體積密度1 776 kg/m3。分別代入仿真模型得到計算結果如圖5所示。為了更加清楚地展示計算結果，僅展示了部分頻率點的數據，下同。

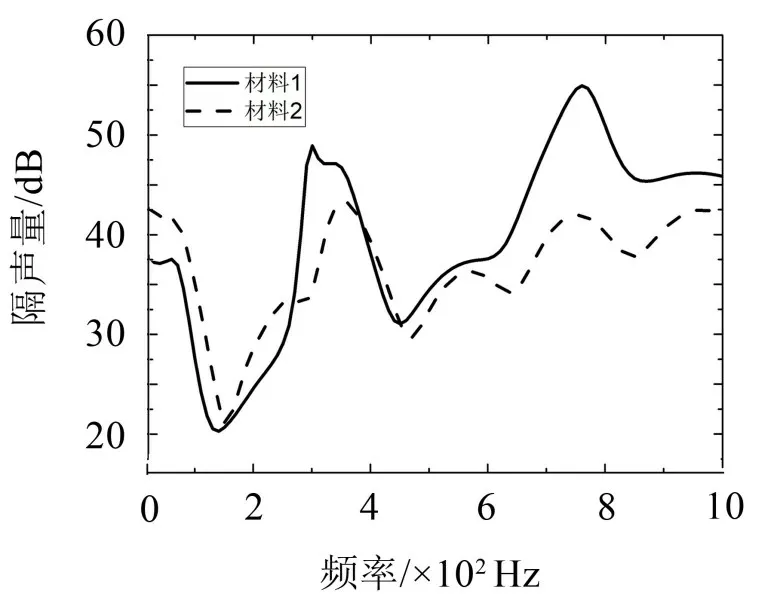
圖5 不同種類夾芯層的結構隔聲特性曲線

由圖5可知，兩種夾芯材料對結構隔聲性能有不同的影響。使用材料1可以在270 Hz到1 000 Hz之間取得良好的隔聲性能；而使用材料2可以在20 Hz到270 Hz之間取得更好的隔聲性能。因此可以考慮綜合使用兩種材料以減少結構質量，提高隔聲性能。

2.3 夾芯層組合方式對結構隔聲的影響

1）材料1與材料2厚度關系為1:2

在原始模型的基礎上將兩種材料的厚度比例設置為1:2分析結構隔聲性能的變化。易知相同的厚度比例有不同的排列方式，材料1和材料2的組合排列方式如圖6所示。求解得到不同結構模型的隔聲性能如圖7所示。

圖6 1:2的不同排列方式

當厚度比例為1:2時，相當于在芯層全為材料2的結構中將一部分芯層替換為材料1有利于結構的輕量化，因此以芯層全為材料2時的隔聲曲線為基準分析不同排列方式下結構隔聲性能的變化規律。由圖7對比發現：

圖7 厚度關系1:2時結構隔聲特性曲線

(1)不同排列方式的結構隔聲特性曲線不同是因為產生了不同的阻抗關系，引起聲能傳遞損失的不同；

(2)根據穿孔板以及板后空腔深度（即夾芯層的厚度）求得穿孔板結構的吸收峰頻率在不填充吸聲材料時為368 Hz，在空腔中填充吸聲材料后將引起吸收峰變寬且稍向低頻移動，因此產生了370 Hz附近吸收峰頻率和峰值的變化；

(3)在630 Hz到1 000 Hz頻段內3種排列方式下結構的平均隔聲量增加比較明顯，這是因為材料1在高頻段的隔聲性能突出，引入材料1后改善了結構的隔聲性能；

(4)雖然排列方式1和排列方式3是關于中面對稱的，但是由于阻尼層的存在以及穿孔板和鋼板不同的聲學屬性，結構整體上并不關于中面對稱，因此兩種方式下結構的隔聲性能存在差異。

2）材料1與材料2厚度關系為2:1

在原始模型的基礎上將兩種材料的厚度比例設置為2:1分析結構隔聲性能的變化。材料1和材料2的組合排列方式如圖8所示。求解得到不同結構模型的隔聲性能如圖9所示。

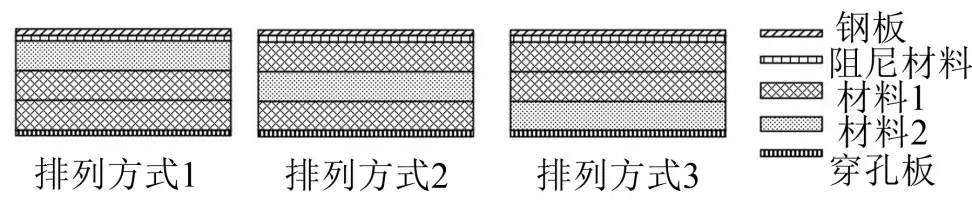
圖8 2:1的不同排列方式

同理當厚度比例為2:1時，相當于在芯層全為材料1的結構中將一部分芯層替換為材料2有利于在厚度不變的情況下增加結構質量，改善結構隔聲性能，因此以芯層全為材料1時的隔聲曲線為基準分析不同排列方式下結構隔聲性能的變化規律。由圖9對比發現：

圖9 厚度關系2:1時結構隔聲特性曲線

(1)在20 Hz到60 Hz范圍內結構的隔聲量增加，630 Hz到1 000 Hz范圍內結構隔聲量降低，這是因為材料2在低頻段隔聲性較好，而在高頻段的隔聲性較差；

(2)370 Hz附近吸收峰的變化同樣是因為穿孔板后添加吸聲材料引起的，但是因為相同的穿孔材料經過不同的組合排列方式后表現出的聲學特性不同，所以引起吸收頻率和峰值的變化也不同；

(3)結構整體上并不關于中面對稱，因此兩種芯層對稱排列方式下結構的隔聲性能存在差異。

3）夾芯材料周期性排列

考慮兩種不同的周期排列方法，一是在材料2中周期性的插入材料1，如圖10所示。在總厚度不變的情況下，逐漸增加排列的周期得到排列方式1、2和3，分析不同排列方式下結構隔聲性能的變化，仿真結果如圖12所示；二是在材料1中周期性地插入材料2，如圖11所示。在總厚度不變的情況下，逐漸增加排列的周期得到排列方式1、2和3，分析不同排列方式下結構隔聲性能的變化，仿真結果如圖13所示

圖10 兩種材料周期排列方法1

圖11 兩種材料周期排列方法2

由圖12和圖13可知，周期排列的不同方式和方法使得結構隔聲性能的差異很大。一是因為每一周期內的阻抗關系不同，二是因為單位厚度內的周期數不同。整體而言，兩種周期構造方法中排列方式1的隔聲性能都是最好的，這是因為相較于其他兩種排列方式，方式1的周期最小所以相同厚度下的周期數最多，使得聲波每穿透一層阻抗都會發生變化，聲波反射次數的增加使得聲能損耗增加。對于周期構造方法1，排列方式1不但獲得了最好的隔聲性能，而且使得結構的質量明顯減少。對于周期構造方法2，排列方式1使得結構在厚度不變、原有吸收峰頻率變化不大的情況下隔聲量明顯增加，有利于在空間有限的情況下保持結構厚度不變，利用現有的材料改善結構的隔聲性能，減少研發新材料的成本。

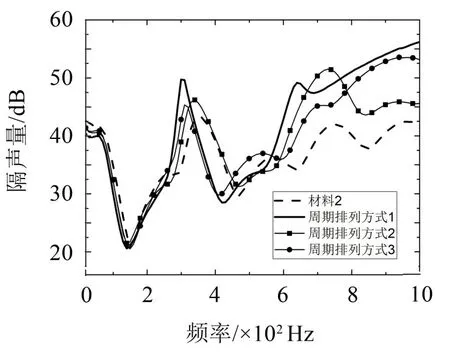
圖12 方法1結構隔聲特性曲線

圖13 方法2結構隔聲特性曲線

3 結語

本文采用FEM-AML直接聲振耦合方法計算了夾層板結構的隔聲量，分析了材料1和材料2不同組合排列方式對結構隔聲性能的影響。結果表明：

(1)兩種不同隔聲特性的夾芯材料混合后的隔聲特性可以相互補償。在高密度芯層材料中加入低密度芯層材料不但可以改善結構的隔聲性能，而且有利于結構的輕量化。在低密度芯層材料中加入高密度芯層材料有利于在空間有限的下情況下保持結構厚度不變，利用現有的材料改善結構的隔聲性能減少研發新材料的成本；

(2)新隔聲特性不但與兩種材料的比例有關，而且還與兩種材料的排列方式有關，不同的排列方式可以構造具有不同聲學屬性的夾芯層；

(3)兩種材料周期排列結構隔聲量的改變比較明顯，不同周期下結構的隔聲性能不同。在20 Hz到1 000 Hz范圍內，周期越小聲波在傳播過程中能量損耗越大，夾層板結構的隔聲性能越好；

(4)改變周期排列的方法和方式可以調整結構的吸收峰頻率向低頻或高頻移動，并且可以調整吸收峰的寬度以及峰值的大小。綜上所述，在工程應用中可以針對不同的噪聲頻譜，采用文中介紹的組合排列方法構造類似的夾層板結構有利于提高結構的隔聲性能、實現結構的輕量化以及減少研發新材料的成本。