加慣質3-PCR隔震平臺振動特性分析

趙猛，王修勇，王文熙

（1.湖南科技大學 結構抗風與振動控制湖南省重點實驗室，湖南 湘潭 411201；2.湖南大學 風工程與橋梁工程湖南省重點實驗室，長沙 410082）

振動是宇宙中普遍存在的一種現象，在生活中也容易感受到振動有頗多的好處，如振動發聲給了人們一個有聲的世界、心臟的振動使生命獲得延續、振動器械搗實混凝土讓人們住上了高樓；當然振動也有不少的壞處，例如地震、車輛振動、機器的振動等等都會影響到人們的生活，這些不良的振動應該抑制或者隔離。目前，振動控制的方法主要有主動控制、被動控制和混合控制。主動控制和混合控制控制振動效果很好，但是需要能量的輸入并且控制系統復雜較難實現。被動控制構造簡單無需能量輸入并且控制效果較好，因此在工程實際中大量運用的是被動控制[1]。

在被動控制中，因為單自由度減振研究得較為成熟和單自由度減振應用范圍的限制，所以多自由度的研究日漸成為重點。隨著人們創新思維愈加活躍，近年來把原本應用于娛樂設施的并聯機構運用到多自由度減振領域中來。Yin等[2]對并聯機構進行了模態分析；馬履中等[3]采用并聯機構做主體結合永磁體和彈簧元件進行多自由度減振分析，介紹了結構及有關參數的設計方法；劉乃軍等[4]設計了一種新型2-PRC-PR(C)并聯機構減振平臺，研究了機構參數對固有頻率的影響；趙偉等[5]基于3-RPC并聯機構的三維振動隔離系統做了試驗研究，隔振系統具有良好的隔振效果；鄧鳴[6]通過牛頓力學方法建立了3-PCR并聯減振平臺運動微分方程并分析了減振特性。

慣質加入減振系統具有諸多的優勢，它能夠靈活地調節結構頻率，提高耗能裝置的耗能效率。Dong[7]研究表明了慣性體有減小系統響應和降低固有頻率的趨勢；蔡龍[8]提出了一種新型的調諧慣質電磁阻尼器（TIMED），其具有更高的阻尼性能，在較小的相對安裝位置就能提供可觀的阻尼力。TIMED可實現很大的等效慣性質量，證明了該模型能夠顯著地提高斜拉索減振效率；李壯壯等[9]提出了4種新型基于ISD（I—慣容，S—彈簧，D—阻尼）結構的被動振動控制減振平臺，通過與傳統動力吸振器在簡諧激勵和隨機激勵下的響應進行比較，發現ISD結構有很好的減振效果。

綜合上述，本文提出一種3-PCR并聯機構為主體，在移動副上并聯慣質彈簧阻尼元件的減振模型。建立了系統運動微分方程，分析了機構固有頻率，研究了減振平臺的減振特性。

1 加慣質3-PCR減振平臺

三平移減振模型如圖1所示。該減振機構由定平臺O1O2O3、動平臺A1A2A3以及連接兩平臺的3個運動支鏈OiDiBiCi(i=1,2,3)組成，其中定平臺、動平臺是兩個邊長不同的等邊三角形且互相平行，3個運動支鏈結構相同，從上至下由轉動副、定長斜桿、圓柱副和移動副構成。機構各部分位置關系：3條運動支鏈繞Z軸等分布置，圓柱副與對應動平臺的邊平行，移動副與定平臺之間的夾角為α，定長斜桿BiCi與定平臺的夾角為θi。該并聯機構的主要特點是保證機構在運動過程中動平臺始終與定平臺保持平行來滿足三平移無轉動。3-PCR并聯機構在移動副兩端并聯具有慣質bi、剛度ki和阻尼ci的慣質彈簧阻尼系統，構成空間三平移減振平臺。

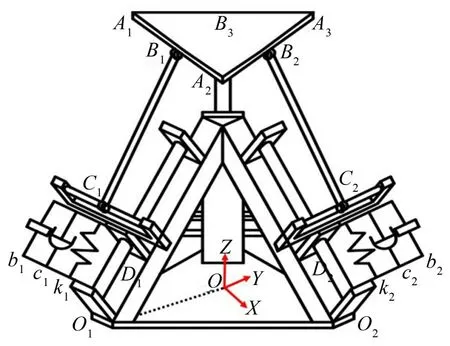
圖1 加慣質3-PCR并聯機構

2 系統運動方程

建立坐標系O-XYZ和Oi-xiyizi(i=1,2,3)，在坐標系O-XYZ中設動平臺形心p的坐標為（xp，yp，zp），通過坐標轉換得到運動約束方程[6]。

式中：a,b分別為定平臺和動平臺的邊長，li(i=1,2,3)為移動副OiDi的長度；hi為定長斜桿BiCi的長度。

化簡(1)式并求解得：

式中：

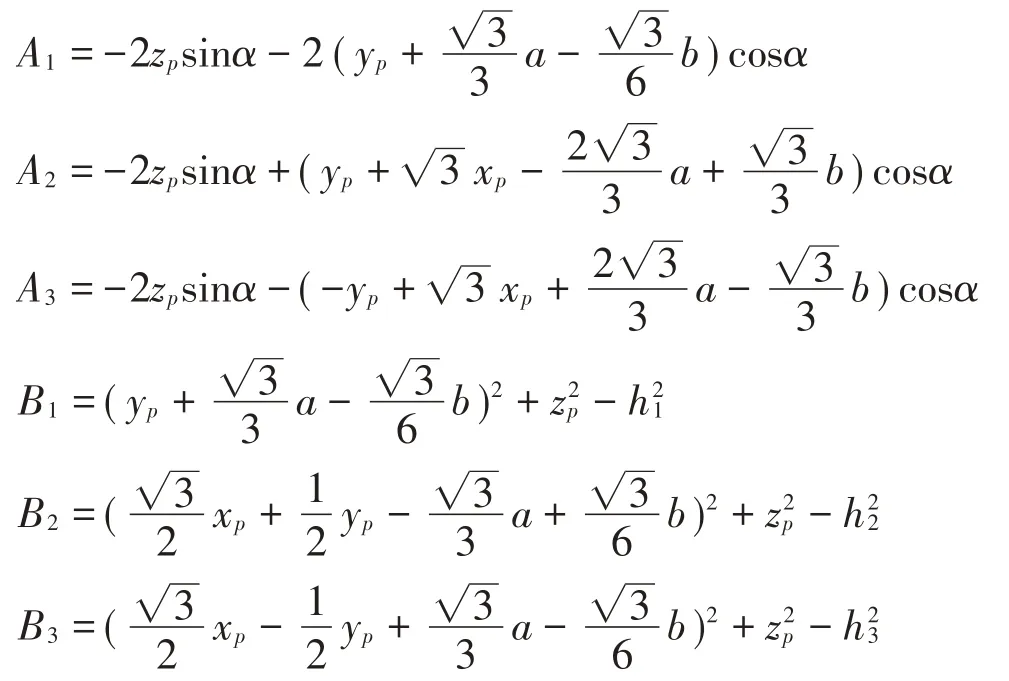
由(2)式對時間求導并化簡得速度反解：

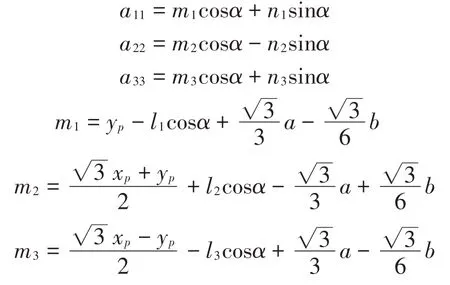
由式(3)對時間求導并化簡得加速度反解：

忽略運動支鏈的質量和摩擦力，由牛頓第二定律分析得平臺運動微分方程：

式中：Qx、Qy、Qz是對定平臺x、y、z方向激勵力，md為動平臺質量，ki為彈簧剛度，c為阻尼，me為慣質，l0為彈簧原長。

3 系統振動特性分析

數值仿真分析采用的參數如表1。

通過無阻尼自由振動時程分析可以得到機構的周期，進而可以求出機構固有頻率。圖2是初始位移為xp=0.005 m、yp=0.005 m、zp=0.525 34 m，且3個方向初始速度均為零的自由振動位移時程曲線，經求得x方向和y方向頻率約為9 Hz，z方向頻率約為26.25 Hz。

圖2 自由振動時程曲線

在x方向對定平臺施加Qx=60 sinωt（N）的簡諧激勵，當只對x方向激勵y、z方向沒有響應，通過對機構進行掃頻和改變系統的慣質，可以得到不同慣質下的頻響曲線如圖3所示。從圖3可以看出，加入慣質后，x方向幅頻曲線發生了一個平移，意味著慣質起到一個負剛度效應，降低了平臺固有頻率，選擇適當的慣質可以避免確定外部激勵下的共振響應，能夠改善3-PCR并聯機構在x方向的隔振性能。

在激勵頻率為9 Hz時得到的位移時程曲線如圖4所示，發現加慣質對系統有較好的減振效果，對比不加慣質的系統減振效果更加優越，并且慣質越大減振效果越好，說明在x方向能夠實現低頻隔振。

在y方向對定平臺施加Qy=60 sinωt（N）的簡諧激勵的仿真結果如圖5、圖6所示。由圖可知，y方向的振動特性和x方向振動特性基本一致。

表1 系統初始參數

圖3 不同慣質條件下x方向蝠頻曲線

圖4 x方向位移時程（激勵頻率9 Hz）

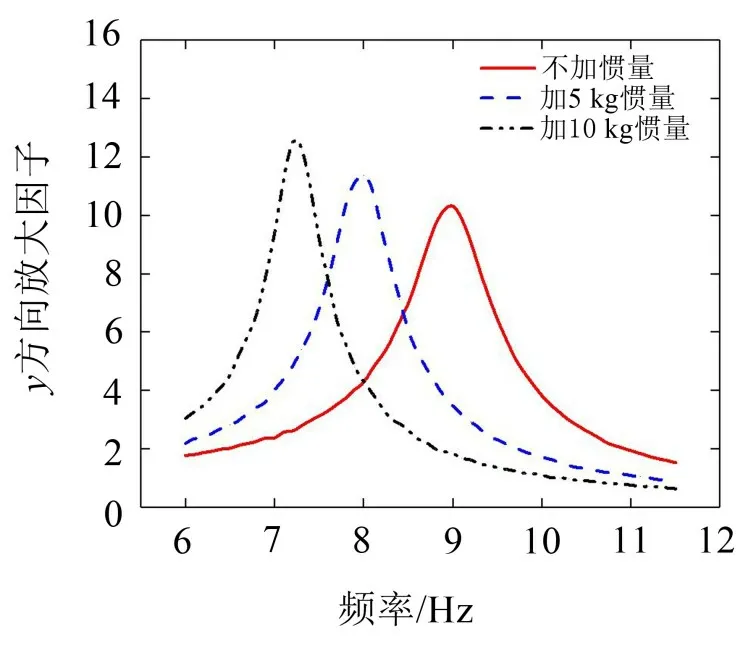
圖5 不同慣質條件下y方向蝠頻曲線

圖6 y方向位移時程（激勵頻率9 Hz）

在z方向對定平臺施加Qz=60 sinωt（N）的簡諧激勵，當只對z方向激勵時x、y方向沒有響應，通過對機構進行掃頻和改變系統的慣質，可以得到不同慣質下的頻響曲線，如圖7所示。由圖可知，慣質能降低z方向頻率，使共振區產生了平移，能夠改善3-PCR并聯機構在z方向的隔振性能。

圖7 不同慣質條件下z方向蝠頻曲線

在激勵頻率為26.25 Hz時得到的z方向位移時程曲線如圖8所示。發現加慣質對系統有較好的減振效果，對比不加慣質的系統減振效果更加優越，并且慣質越大減振效果越好，說明在z方向能夠實現低頻隔振。

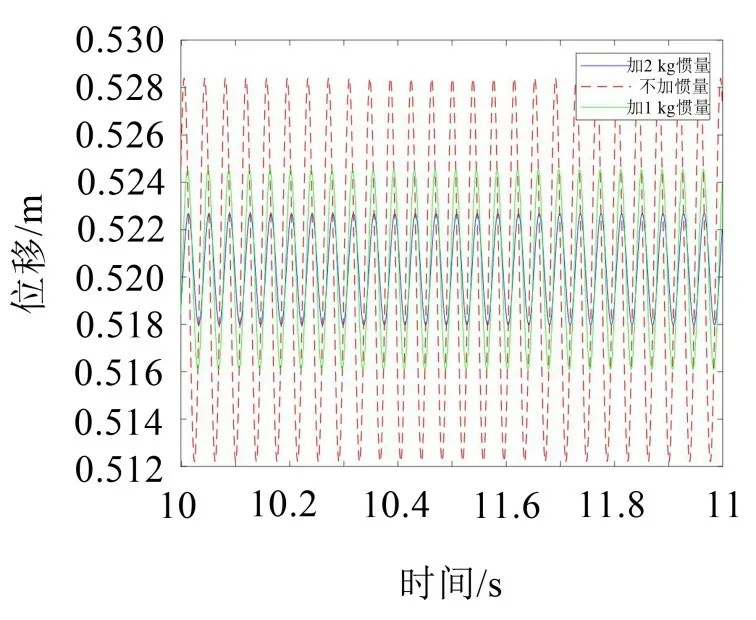
圖8 z方向位移時程（激勵頻率26.25 Hz）

4 對系統輸入地震波的振動性能分析

采用EI波對系統定平臺x、y、z3個方向分別進行激勵，分析地震響應特征。圖9為EI波加速度時程圖，圖10、圖11、圖12分別為x、y、z方向加速度響應曲線，圖13、圖14、圖15分別為x、y、z方向位移響應曲線。通過增速處理，1 kg的實際質量可以實現3 200 kg的慣質系數[10]。當慣質為25 000 kg，阻尼為20 000 N·s/m時，通過掃頻求得x、y、z方向的固有頻率分別為0.24 Hz、0.24 Hz、0.43 Hz，在EI波作用下加慣質對比不加慣質3-PCR并聯機構加速度和位移響應明顯降低，加速度響應比位移響應減振效果更為明顯。說明加慣質后機構能夠對地震作用起到良好的隔振效果，可以大幅調節機構頻率，靈活的拓寬減震頻帶。

圖9 EI波加速度時程曲線

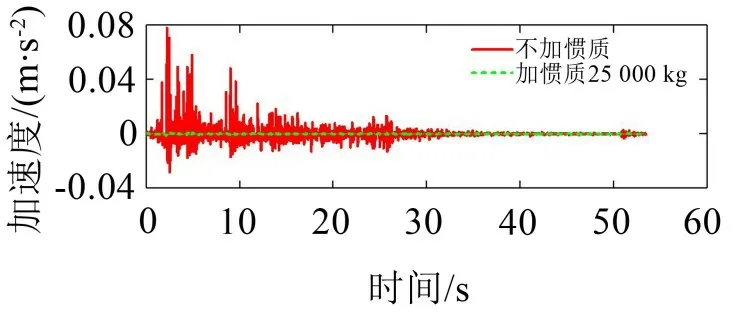
圖10 x方向加速度時程曲線

圖11 y方向加速度時程曲線

圖12 z方向加速度時程曲線

圖13 x方向位移時程曲線

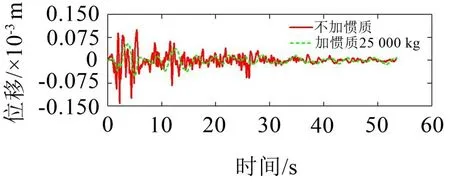
圖14 y方向位移時程曲線

圖15 z方向位移時程曲線

5 結語

本文針對加慣質3-PCR減振平臺隔震特性進行仿真分析，得到以下主要結論：

（1）慣質引起了負剛度效應，慣質能改變3-PCR減振平臺的固有頻率，慣質越大，平臺固有頻率越低。另外，加慣質后能夠改善3-PCR并聯機構隔振效果，同時能夠實現三維低頻隔振，為三維低頻隔振提供了有利的理論基礎；

（2）增加慣質后減振平臺幅頻曲線產生了一個平移，通過設計不同的慣質參數，可以大幅調節機構頻率，靈活的拓寬減震頻帶。可以避免確定頻率激勵下的共振響應，從而達到預期的隔振效果；

（3）優化慣質參數，加慣質3-PCR減振平臺對簡諧激勵和地震荷載都能起到良好的隔震效果。