缺失數(shù)據(jù)條件下基于GAN與LSTM的水文預(yù)報研究
秦 鵬,陳 雨,盧文龍
(1.四川大學(xué) 電子信息學(xué)院,四川 成都610065;2.成都萬江港利科技股份有限公司,四川 成都610041)
水文預(yù)報[1]旨在根據(jù)某一區(qū)域或某一水文站的歷史水文氣象數(shù)據(jù)對河流水文情勢進(jìn)行定性或定量預(yù)測,是防洪調(diào)度決策、生態(tài)環(huán)境保護(hù)、水資源綜合開發(fā)利用等的重要依據(jù)。水文預(yù)報方法可分為傳統(tǒng)方法和新方法兩大類。傳統(tǒng)的中長期預(yù)報方法主要是根據(jù)河川徑流的變化具有連續(xù)性、周期性、地區(qū)性和隨機(jī)性等特點來開展研究,主要有成因分析和水文統(tǒng)計方法[2]。ARIMA模型[3]的基本思想是通過差分消除序列中的趨勢項,將非平穩(wěn)序列轉(zhuǎn)化為平穩(wěn)序列,逐漸應(yīng)用于水文預(yù)報[4-5];李亞偉等[6]提出的SVR模型建立在VC維概念和結(jié)構(gòu)風(fēng)險最小化原理基礎(chǔ)上,根據(jù)有限的樣本信息在模型的學(xué)習(xí)精度和學(xué)習(xí)能力之間尋求最佳組合,也成功應(yīng)用于水文預(yù)報。近年來,隨著計算機(jī)技術(shù)的發(fā)展和新的數(shù)學(xué)方法的不斷涌現(xiàn),針對復(fù)雜的水文水資源時間序列問題,具有極強(qiáng)的自適應(yīng)學(xué)習(xí)能力和非線性映射能力的深度神經(jīng)網(wǎng)絡(luò)方法應(yīng)運(yùn)而生,如人工神經(jīng)網(wǎng)絡(luò)(ANN)、遞歸神經(jīng)網(wǎng)絡(luò)(RNN)、卷積神經(jīng)網(wǎng)絡(luò)(CNN)以及長短時記憶網(wǎng)絡(luò)(LSTM)。
水文數(shù)據(jù)是對大自然發(fā)生的水文情況實時、連續(xù)、長期觀察記錄的結(jié)果,具有序列性、實時性、海量性等特點。數(shù)據(jù)缺失在水文學(xué)研究中是一個常見的問題,其產(chǎn)生的原因多種多樣,包括測量儀器的損壞、環(huán)境的干擾以及人工記錄中的誤差等[7]。數(shù)據(jù)缺失通常會降低水文模型統(tǒng)計分析的準(zhǔn)確性[8],甚至?xí)斐蓪蓚€或多個變量之間的時序關(guān)系進(jìn)行有偏的估計[9]。這兩種問題(準(zhǔn)確性驟降和估計偏差)都可能導(dǎo)致在分析存在數(shù)據(jù)缺失的數(shù)據(jù)集時受到極大的干擾,從而得出不正確的結(jié)論[10]。因此,水文數(shù)據(jù)的質(zhì)量和完整性對于水文預(yù)報模型至關(guān)重要。
水文數(shù)據(jù)是典型的時間序列數(shù)據(jù),為了解決時間序列預(yù)測模型因數(shù)據(jù)缺失而導(dǎo)致的精度、性能等問題,有關(guān)學(xué)者已經(jīng)提出了多種方法。最早的解決方案是直接省略缺失數(shù)據(jù),僅采用觀測到的數(shù)據(jù)。但是當(dāng)數(shù)據(jù)缺失較嚴(yán)重時,模型的性能將非常差。張升堂等[11]提出一種線性插值模型,該模型采用缺失數(shù)據(jù)站點鄰近的3個位置生成一個時空插值平面進(jìn)行線性插值。謝景新[12]提出由一系列已知觀測點形成一條光滑曲線,通過求解三彎矩陣方程得出曲線函數(shù)組繼而對缺失站點進(jìn)行插值的三次樣條插值法,但是無論是線性插值還是樣條插值都僅僅是對缺失數(shù)據(jù)的一次平滑和近似擬合,無法挖掘到缺失數(shù)據(jù)的隱藏信息。王方超等[13]提出了一種調(diào)整最大似然法,不引入外部信息,根據(jù)數(shù)據(jù)自身的特性進(jìn)行插值,是一種數(shù)據(jù)驅(qū)動估算法。此外還有基于回歸的估算、基于主成分分析的數(shù)據(jù)估算等方法作為改進(jìn)的插補(bǔ)方法被提出來,這些方法雖然改善了插值精度,提高了統(tǒng)計分析的準(zhǔn)確性,但是仍然無法解決估計偏差的問題。水文數(shù)據(jù)是時間序列數(shù)據(jù),其各個特征在時間序列上呈高度相關(guān)性,缺失值的估算應(yīng)考慮水文數(shù)據(jù)的時間序列性質(zhì)。
近年來,循環(huán)神經(jīng)網(wǎng)絡(luò)(RNN)中的長短時記憶網(wǎng)絡(luò)(LSTM)和門控循環(huán)單元網(wǎng)絡(luò)(GRU)在關(guān)于時間序列數(shù)據(jù)的應(yīng)用上具有優(yōu)秀的表現(xiàn),例如機(jī)器翻譯和文本識別。RNN可以通過反饋連接的時間延遲單元捕獲輸入序列的動態(tài)時間關(guān)系,學(xué)習(xí)水文系統(tǒng)的順序或時變模式,展示了強(qiáng)大的預(yù)測性能。生成對抗網(wǎng)絡(luò)(GAN)模型具有學(xué)習(xí)原始數(shù)據(jù)分布生成數(shù)據(jù)的特點,Goodfellow等[14]、王萬良等[15]從理論上證明了當(dāng)GAN模型達(dá)到收斂狀態(tài)時,生成數(shù)據(jù)具有和真實數(shù)據(jù)相同的分布。筆者在存在缺失的水文數(shù)據(jù)集中引入GAN模型,把GRU作為生成器,把CNN作為判別器,通過對抗學(xué)習(xí),為數(shù)據(jù)集中的缺失部分填充與真實數(shù)據(jù)分布一致的生成數(shù)據(jù)。該生成數(shù)據(jù)與真實數(shù)據(jù)分布趨于一致,而且可以表征缺失數(shù)據(jù)的時序特性,是高質(zhì)量的填充數(shù)據(jù)。因此,GAN模型為上述問題提供了更好的解決方案。與此同時,將GAN模型與長短時記憶網(wǎng)絡(luò)(LSTM)結(jié)合,提出了一種新的耦合模型GAN-LSTM(簡稱為GANL)。該模型由GAN和LSTM兩個子模型耦合組成,首先通過GAN模型對數(shù)據(jù)缺失部分進(jìn)行填充,整合出高質(zhì)量的數(shù)據(jù),解決目前水文預(yù)報中常見的數(shù)據(jù)缺失問題;然后通過GAN模型整合出的數(shù)據(jù)來訓(xùn)練LSTM模型,進(jìn)行預(yù)測處理。該模型不僅有效改善了缺失數(shù)據(jù)的問題,而且可以捕獲水文時間序列觀測值的長期相關(guān)性,利用缺失信息來改善預(yù)測性能,從而有效地實現(xiàn)數(shù)據(jù)缺失條件下的水文預(yù)報。
1 生成對抗網(wǎng)絡(luò)介紹
受博弈論中的二人零和博弈(two-player game)啟發(fā),Goodfellow開創(chuàng)性地提出了GAN模型。在二人零和博弈中,博弈雙方的利益之和為零或一個常數(shù),即一方有所得,另一方必有所失。GAN模型中的博弈雙方分別由生成模型G(generative model)和判別模型D(discriminative model)組成,將隨機(jī)變量作為生成模型的輸入,經(jīng)過其非線性映射,輸出對應(yīng)的信號作為判別模型的輸入,由判別模型來判斷該信號來自于真實數(shù)據(jù)的概率。在訓(xùn)練過程中,生成器努力地欺騙判別器,而判別器努力地學(xué)習(xí)如何正確區(qū)分真假樣本,這樣,兩者就形成了對抗的關(guān)系,最終目標(biāo)就是讓生成器生成足以以假亂真的偽樣本。GAN模型在計算機(jī)視覺領(lǐng)域已得到成功運(yùn)用,如圖像修復(fù)、語義分割和視頻預(yù)測[16-18]。
2 模型設(shè)計
GANL模型(如圖1所示)主要完成兩方面的任務(wù):一是學(xué)習(xí)數(shù)據(jù)分布、捕獲缺失信息,生成缺失數(shù)據(jù)以整合出高質(zhì)量的數(shù)據(jù);二是將整合出的數(shù)據(jù)作為訓(xùn)練數(shù)據(jù),訓(xùn)練預(yù)測模型、進(jìn)行有效的水文預(yù)報。圖1左半部分描述的是GAN模型,由生成器GRU和判別器CNN組成。將觀測數(shù)據(jù)、缺失標(biāo)志組成的聯(lián)合向量作為生成器的輸入,在經(jīng)過GRU訓(xùn)練后形成一種新的特征表示,然后將新特征傳入判別器CNN中,由判別器CNN來鑒別傳過來的新特征分布是否與真實歷史數(shù)據(jù)的分布趨于一致,如果一致則可以作為最終生成數(shù)據(jù)對缺失數(shù)據(jù)進(jìn)行填充,繼而作為圖1右側(cè)預(yù)測模型的訓(xùn)練數(shù)據(jù),如果不一致則重新傳回GRU層進(jìn)行重復(fù)對抗訓(xùn)練。圖1右側(cè)描述的是LSTM模型,此部分模型輸入的是由GAN模型傳來的整合填充過的多變量時序數(shù)據(jù)(流量、降雨量、蒸發(fā)量等),輸出是預(yù)測值(水位等)。
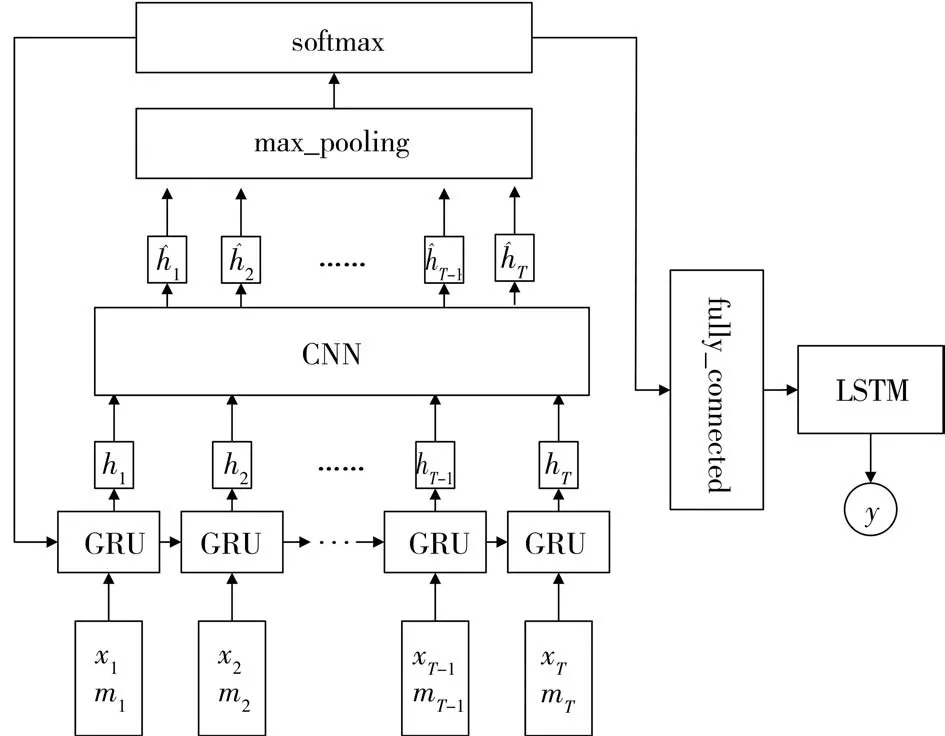
圖1 GANL模型
2.1 GAN子模型
GAN模型包含生成模型和判別模型兩個模塊。生成模型接收隨機(jī)信號作為輸入,經(jīng)過某種映射后又將輸出信號作為判別模型的輸入,由判別模型來判斷該信號來自真實數(shù)據(jù)的概率。因此,兩個模塊的目標(biāo)是完全相反的,生成模型的目標(biāo)是最小化對數(shù)似然函數(shù),使得輸出信號與真實數(shù)據(jù)的分布趨于一致,而判別模型的目標(biāo)則是用最大化對數(shù)似然函數(shù)判斷輸入信號是否來源于真實數(shù)據(jù)。利用GAN模型可以學(xué)習(xí)數(shù)據(jù)分布生成數(shù)據(jù)的特點,將觀測數(shù)據(jù)和缺失標(biāo)志組成的聯(lián)合數(shù)據(jù)作為生成模型的輸入,經(jīng)過非線性映射將聯(lián)合數(shù)據(jù)的特征分布傳遞給判別模型,然后由判別模型來判斷生成的特征分布和真實數(shù)據(jù)的特征分布的異同,反復(fù)對抗訓(xùn)練直到判別器無法判斷兩者的區(qū)別,此時判別模型的輸出結(jié)果就是要填充的缺失數(shù)據(jù)。CNN上面的max_pooling層對CNN的輸出特征進(jìn)行降采樣池化操作,softmax層判斷新特征分布是否與原數(shù)據(jù)分布一致,fully_connected層對特征空間維度進(jìn)行轉(zhuǎn)換以方便后續(xù)的預(yù)測。
2.1.1 GRU生成模型
用長度為T的D維向量表示一個多元時間序列水文數(shù)據(jù),記為X=(x1,x2,…,x T),其中每一個時刻的x都有D個變量表示t時刻變量d的觀測值。引入一個D維的缺失標(biāo)志向量m t∈{0,1}D來表示t時刻的觀測變量是否缺失。

GRU結(jié)構(gòu)如圖2所示,對于每個時刻的隱藏單元,GRU都有一個復(fù)位門r t和更新門z t來控制隱藏特征h t,更新方式如下:
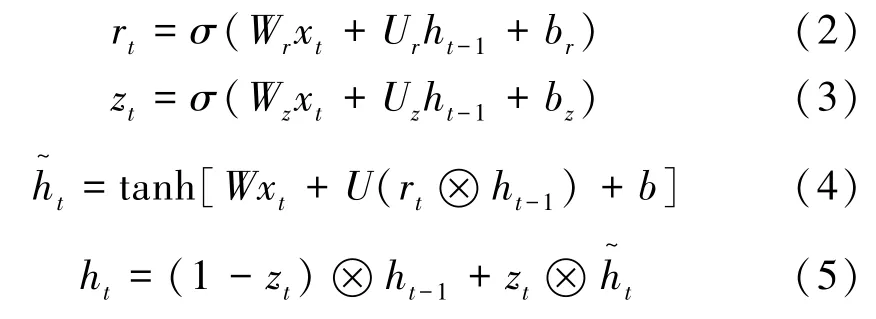
式中:W z,W r,W,U z,Ur,U和bz,b r,b均為可以學(xué)習(xí)的參數(shù),表示連接各個門的權(quán)重;σ()為Sigmoid函數(shù);?為element-wise乘法(矩陣的對位元素依次相乘)。
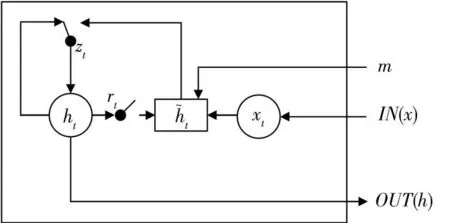
圖2 GRU結(jié)構(gòu)
2.1.2 CNN判別模型
將卷積神經(jīng)網(wǎng)絡(luò)CNN作為判別模型,將GRU的輸出結(jié)果h t轉(zhuǎn)化為新的特征表示
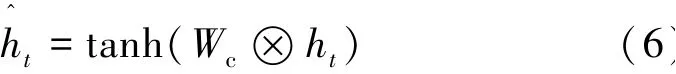
式中:h t為GRU提取的特征為判別模型CNN生成的特征;Wc為CNN的模型參數(shù)。
接下來采用池化層提取重要特征,然后將提取出的特征輸入到softmax層,根據(jù)映射的概率值來判斷是否和原始數(shù)據(jù)分布一致。如果一致則可以作為整合數(shù)據(jù)通過全連接層輸入到圖1右邊的預(yù)測模型中。
2.1.3 GAN模型目標(biāo)函數(shù)
GAN模型的學(xué)習(xí)過程是生成模型和判別模型反復(fù)對抗訓(xùn)練的過程,兩個模型的目標(biāo)截然相反,本質(zhì)上一個是最小化、另一個是最大化問題,這個最小最大優(yōu)化目標(biāo)表示如下:
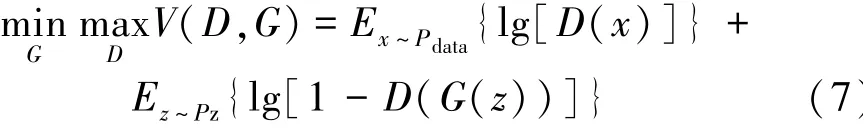
式中:D表示判別器;G表示生成器;D(x)為判別器的輸出;G(z)為生成器的輸出;Pdata為輸入數(shù)據(jù)的分布;Pz為生成數(shù)據(jù)的分布;V為Pdata和Pz兩個分布的jensen-shannon差異。
實際訓(xùn)練中,GAN模型收斂的過程是非常緩慢的。在GAN模型訓(xùn)練過程中,默認(rèn)判別模型的判別能力比生成模型的數(shù)據(jù)生成能力強(qiáng),這樣判別模型才能指導(dǎo)生成模型朝好的方向?qū)W習(xí),因此通常的做法是先更新判別模型的參數(shù)多次,再更新生成模型的參數(shù)一次。本文借鑒文獻(xiàn)[19]的做法,分別為判別模型和生成模型設(shè)置不同的學(xué)習(xí)率,以加快判別模型的收斂速度。
2.2 LSTM子模型
水文數(shù)據(jù)是典型的時間序列數(shù)據(jù),數(shù)據(jù)間有較強(qiáng)的關(guān)聯(lián)性。LSTM是一種循環(huán)神經(jīng)網(wǎng)絡(luò),通過內(nèi)部特有的門控狀態(tài)來記憶長遠(yuǎn)的歷史數(shù)據(jù)并且捕捉隨時間變化的特征信息,因此選擇LSTM作為預(yù)測模型,接收GAN模型整合出的數(shù)據(jù)進(jìn)行預(yù)測,其計算過程為
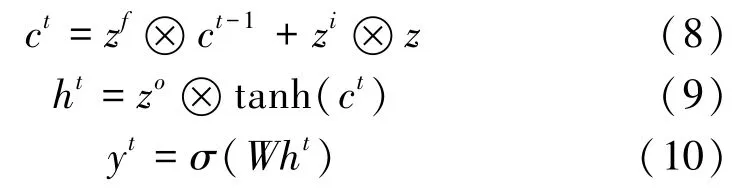
式中:h t為隱藏傳遞狀態(tài);z為當(dāng)前輸入和上一個傳遞狀態(tài)h t-1的向量乘積;z f,z i,z o為內(nèi)部的門控信號;ct為當(dāng)前時間步的內(nèi)部細(xì)胞狀態(tài);y t為當(dāng)前時間步的輸出;W為連接各個門的權(quán)重。
3 試驗設(shè)計及結(jié)果分析
設(shè)計對比試驗,以研究不同模型在數(shù)據(jù)缺失條件下的預(yù)測性能。以清溪水文站的實測水文數(shù)據(jù)集為例,展示了模型的性能,并與目前幾種經(jīng)典的水文預(yù)報方法進(jìn)行比較。
3.1 數(shù)據(jù)集
采用清溪河清溪水文站從2003年1月1日到2005年9月26日共計1 000 d的觀測數(shù)據(jù)作為試驗數(shù)據(jù)。由于設(shè)備損毀、人為失誤等因素造成了部分?jǐn)?shù)據(jù)缺失,因此1 000 d里實際觀測記錄數(shù)據(jù)的只有882 d,缺失了118 d的數(shù)據(jù)。
水文站的監(jiān)測信息紛繁眾多,包括水位、流量、流速、含沙量、降雨量、蒸發(fā)量、流向、水質(zhì)等。眾多相關(guān)性不強(qiáng)的外部特征會影響模型收斂速度,為了解決預(yù)測模型收斂速度慢的問題,用極端梯度提升法[20]提取最為重要的3個特征并將其作為輸入指標(biāo)。也就是說,每一刻的輸入數(shù)據(jù)由3個變量(流量、降雨量、蒸發(fā)量)組成,然后定義水位為預(yù)測輸出值。
試驗中的實測數(shù)據(jù)集缺失部分主要是輸入變量,但難免有輸入數(shù)據(jù)和輸出數(shù)據(jù)均缺失的情況發(fā)生。本文所提出的模型是一個插補(bǔ)和預(yù)測相結(jié)合的耦合模型,其中GAN模型屬于插補(bǔ)模型,填充的是輸入數(shù)據(jù)如降雨量、蒸發(fā)量、流量。對于輸入數(shù)據(jù)和輸出數(shù)據(jù)同時缺失的情況,仍然利用GAN模型填充輸入數(shù)據(jù)并在相應(yīng)的輸出數(shù)據(jù)處做一個標(biāo)記位,最后利用K近鄰算法對標(biāo)記位上的數(shù)據(jù)進(jìn)行填充,最大限度地降低這種極端惡劣的數(shù)據(jù)缺失情況對預(yù)測模型的影響。由于本實例應(yīng)用中數(shù)據(jù)量相對較少且時間序列預(yù)測法適宜于短期預(yù)測,因此將對比試驗設(shè)置成預(yù)見期為3 d的短期水文預(yù)報。短期水文預(yù)報中水文數(shù)據(jù)的時序性和完整性非常重要,所以各種情況下的缺失數(shù)據(jù)都應(yīng)填充后作為模型的訓(xùn)練要素輸入模型。
3.2 基準(zhǔn)模型
對比試驗中采用K近鄰算法作為填充數(shù)據(jù)的基準(zhǔn)方法,即把缺失數(shù)據(jù)鄰近點的加權(quán)平均值作為估算的填充數(shù)據(jù)。同時在采用K近鄰算法填充數(shù)據(jù)后的預(yù)測模型中使用水文預(yù)報中經(jīng)典的SVR模型和ARIMA模型的組合模型作為GANL模型的試驗對比模型,試驗環(huán)境和參數(shù)設(shè)置如下。
SVR模型中的內(nèi)核函數(shù)用于更改輸入空間的維數(shù),從而產(chǎn)生更為可靠的回歸,對模型預(yù)測性能的改善起著至關(guān)重要的作用。核函數(shù)有多種,如線性、多項式、徑向基函數(shù)、多層感知等,本文選用徑向基核函數(shù)RBF。同時選用兩步網(wǎng)格搜索方法對SVR參數(shù)進(jìn)行了優(yōu)化,與傳統(tǒng)方法(例如反復(fù)試驗)相比,可以更有效、更系統(tǒng)地校準(zhǔn)參數(shù)。本文所采用的SVR模型是利用Chang和Lin開發(fā)的LIBSVM工具箱建立的。
為了使ARIMA模型適用于水文時間序列數(shù)據(jù)并進(jìn)行有效預(yù)測,采用模型識別、參數(shù)估計和診斷檢查3個步驟來建立最優(yōu)模型。在識別階段,將經(jīng)驗自相關(guān)模式與理論模式進(jìn)行匹配,使用自相關(guān)函數(shù)(ACF)和部分自相關(guān)函數(shù)(PACF)來確定最佳擬合模型參數(shù)(p,d,q),其中:p表示模型中滯后觀測值的數(shù)量,d表示原始觀測值相差的次數(shù),q表示移動平均窗口的大小。通過觀察序列的自相關(guān)函數(shù)和偏相關(guān)函數(shù)圖,初步確定模型參數(shù):p=0~5,d=0~2,q=0~2。一旦確定了暫定模型,就可以直接估算模型參數(shù),使誤差最小化。參數(shù)估計可以使用非線性優(yōu)化程序來完成。模型構(gòu)建的最后一步是對模型進(jìn)行適當(dāng)?shù)脑\斷檢查。如果模型不夠好,則應(yīng)確定一個新的暫定模型,然后再次進(jìn)行參數(shù)估計和模型驗證。通過多輪對比試驗,本文選擇了參數(shù)為(5,1,0)的ARIMA模型。
3.3 評價指標(biāo)
由于填充數(shù)據(jù)的質(zhì)量高低不能直觀展示,因此各模型性能均通過整合后數(shù)據(jù)的最終預(yù)測結(jié)果表現(xiàn)來體現(xiàn)。為了從多角度衡量模型的預(yù)測效果,本文采用平均絕對誤差(MAE)、平均絕對百分比誤差(MAPE)、均方根誤差(RMSE)作為預(yù)測準(zhǔn)確性的度量指標(biāo),公式如下:
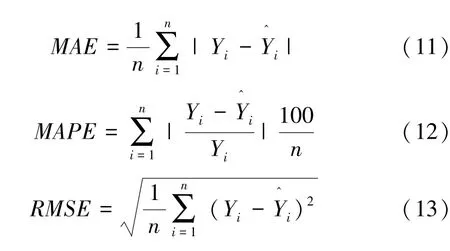
式中:Yi為實測值為預(yù)測值。
3.4 試驗結(jié)果分析
為了驗證本文所提出的模型在缺失數(shù)據(jù)條件下的預(yù)測性能,分別與采用了K近鄰算法填充數(shù)據(jù)后的SVR模型和ARIMA模型進(jìn)行了預(yù)見期為3 d的水文預(yù)報對比試驗。試驗將填充整合后前800 d數(shù)據(jù)作為訓(xùn)練集,后200 d數(shù)據(jù)作為測試集,結(jié)果如圖3所示。
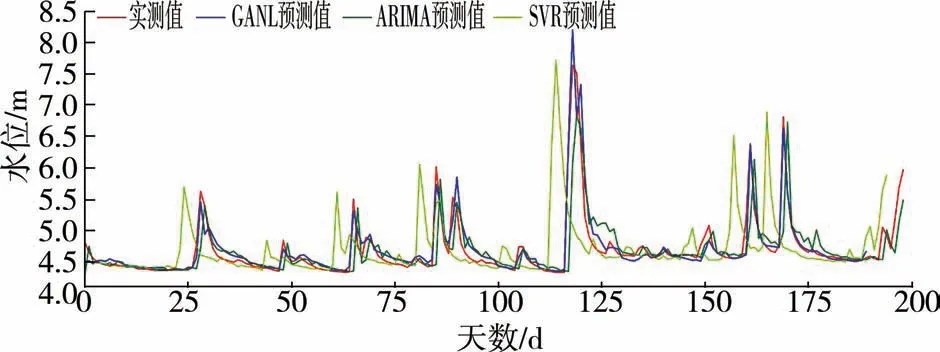
圖3 填充數(shù)據(jù)后各模型預(yù)測結(jié)果比較
與此同時,設(shè)置完全相同的試驗環(huán)境和參數(shù)直接對原始實測數(shù)據(jù)在各模型下進(jìn)行水文預(yù)報對比試驗,結(jié)果如圖4所示。
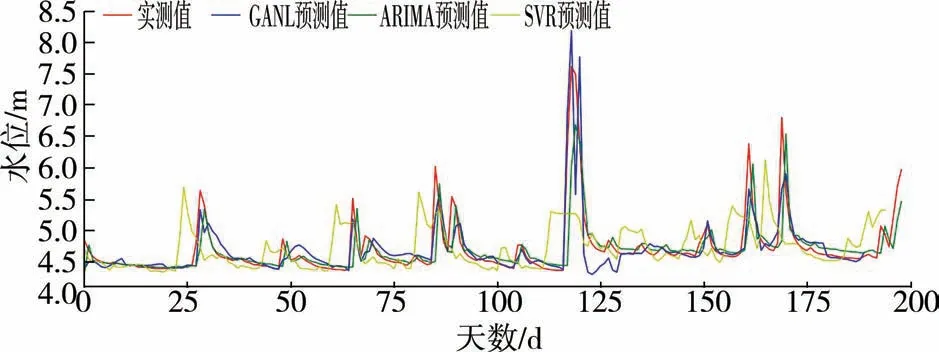
圖4 實測數(shù)據(jù)下各模型預(yù)測結(jié)果比較
對比圖3、圖4發(fā)現(xiàn),填充后的數(shù)據(jù)擬合結(jié)果顯著優(yōu)于有缺失的實測數(shù)據(jù)擬合結(jié)果。
圖3 中各個模型預(yù)測值在訓(xùn)練集和測試集中的平均絕對誤差(MAE)、平均絕對百分比誤差(MAPE)和均方根誤差(RMSE)分別見表1和表2。

表1 訓(xùn)練集模型性能對比
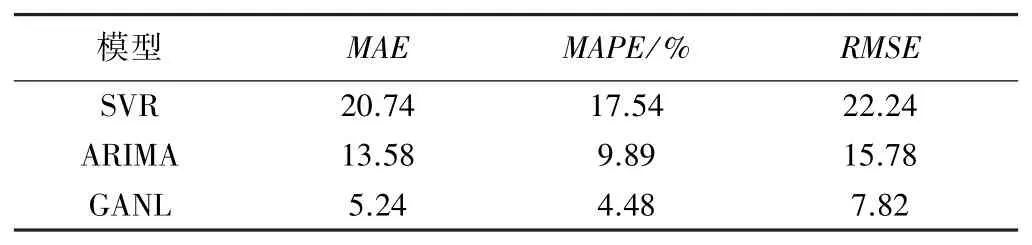
表2 測試集模型性能對比
從表1、表2可以直觀地看出,本文所提出的模型在缺失數(shù)據(jù)條件下的預(yù)測性能強(qiáng)于另外兩個模型。圖3展示了各個模型的預(yù)測結(jié)果和實測值的擬合情況,其中SVR模型的預(yù)測效果最糟糕,這是因為SVR模型在數(shù)據(jù)缺失條件下的魯棒性很差,無法挖掘缺失數(shù)據(jù)的隱藏信息甚至可能在填充數(shù)據(jù)后引入了缺失值和預(yù)測值間本來不存在的關(guān)系,導(dǎo)致模型性能急劇下降;ARIMA模型預(yù)測擬合結(jié)果整體較好,魯棒性強(qiáng)于SVR模型,但是仔細(xì)觀察可以發(fā)現(xiàn)模型在部分峰值處預(yù)測效果較差,這是因為ARIMA模型對缺失數(shù)據(jù)采用K近鄰算法進(jìn)行填充,是一種簡單的線性平滑處理,如果碰到本身就是峰值數(shù)據(jù)且出現(xiàn)缺失這種情況的話,就無法有效利用鄰近數(shù)據(jù)挖掘缺失信息,存在估計偏差的問題,預(yù)測性能就會受到影響;GANL模型的預(yù)測結(jié)果最好,這是因為它可以在對抗中學(xué)習(xí)數(shù)據(jù)分布并生成高質(zhì)量的填充數(shù)據(jù),不再受到數(shù)據(jù)缺失的限制,最大限度減弱填充數(shù)據(jù)時多變量間估計偏差的影響。
4 結(jié) 論
通過生成對抗網(wǎng)絡(luò)在存在缺失的數(shù)據(jù)集上挖掘數(shù)據(jù)缺失信息、填充高質(zhì)量的數(shù)據(jù),可以緩解當(dāng)前水文預(yù)報中常見的數(shù)據(jù)缺失問題。將插補(bǔ)模型GAN和預(yù)測模型LSTM進(jìn)行深度結(jié)合,提出的GANL模型,能夠在數(shù)據(jù)缺失條件下實現(xiàn)可靠有效的預(yù)測。以清溪河清溪水文站的實測水文數(shù)據(jù)為例,對GANL模型進(jìn)行了試驗評估,結(jié)果表明,在數(shù)據(jù)缺失條件下其性能顯著優(yōu)于其他模型。
- 人民黃河的其它文章
- 陜西黃河流域生態(tài)保護(hù)和森林植被高質(zhì)量發(fā)展建設(shè)對策
- 加強(qiáng)水利工程經(jīng)濟(jì)管理的方法研究
——評《水利經(jīng)濟(jì)與水利工程管理》 - 水利風(fēng)景區(qū)水文化遺產(chǎn)的保護(hù)與開發(fā)
——評《中國水文化遺產(chǎn)考略》 - 黃河文化旅游資源開發(fā)研究
——評《黃河流域旅游文化及其歷史變遷》 - 新時代黃河流域生態(tài)治理機(jī)制研究
——評《黃河流域生態(tài)保護(hù)和高質(zhì)量發(fā)展報告》 - 水利水電工程建設(shè)安全生產(chǎn)管理現(xiàn)狀及評價機(jī)制
——評《水利水電工程建設(shè)安全生產(chǎn)管理》

