使用零力矩點反饋的雙足機器人慣性參數(shù)辨識

吳偉國，高力揚

(哈爾濱工業(yè)大學 機電工程學院 仿生仿人機器人及其智能運動控制研究室, 哈爾濱 150090)

準確的動力學模型是獲得良好控制效果的前提之一，因此在對實際機器人進行控制實驗之前，往往需要進行參數(shù)辨識，以減少控制器中理論模型的誤差。參數(shù)辨識的研究對象大多為機器人操作臂等有根系統(tǒng)[1-3]，對系統(tǒng)的Lagrange方程或牛歐方程進行線性化[4-5]，可得到如下方程：

(1)

式中：τ和τf分別為關節(jié)的驅(qū)動力矩和摩擦力矩矢量，q為關節(jié)角矢量，Y為由關節(jié)運動確定的回歸矩陣，Φ為由待辨識的基底參數(shù)組成的矢量。

根據(jù)回歸矩陣Y的行列式[6]或條件數(shù)[7]對參數(shù)辨識時機器人的運動軌跡進行優(yōu)化，使Φ中的參數(shù)得到充分激勵，對不同時刻的測量數(shù)據(jù)進行組合，使用最小二乘法[1-2]或其他優(yōu)化求解算法[3]對式(1)中的函數(shù)進行擬合，即可得到最優(yōu)的模型參數(shù)。

近年來，隨著機器人操作臂的參數(shù)辨識技術日趨成熟，研究者們將目光轉向了包含雙足機器人在內(nèi)的多支鏈無根系統(tǒng)，一部分研究中直接使用與機器人操作臂相同的方法，將雙足機器人的某個桿件固定，對不同的運動學支鏈單獨進行識別。例如He等[8]將仿人機器人的軀干固定，根據(jù)關節(jié)力矩數(shù)據(jù)對機器人的手臂慣性參數(shù)進行了辨識；熊文英[9]將雙足機器人的軀干固定，對大腿和小腿的慣性參數(shù)進行了參數(shù)辨識；Iwasaki等[10]固定雙足機器人的右腳，進行了HRP-2機器人的參數(shù)辨識仿真。

上述參數(shù)辨識方法無法得到被固定桿件的慣性參數(shù)，且辨識結果受關節(jié)摩擦的不確定性影響，會產(chǎn)生一定誤差。為解決上述問題，Ayusawa等[11]對足式機器人的一般動力學模型[12]進行變形處理，得到參數(shù)辨識方程:

(2)

提出了足式機器人慣性參數(shù)辨識的基準桿件方法。

其中:qO為由基準桿件位姿矢量qB和機器人關節(jié)角矢量q組成的觀測矢量，qO=[qBT,qT]T；YO是考慮基準桿件運動的回歸矩陣；NL是機器人足的數(shù)量；Fi是第i個足的六維力矢量；Ji是第i個足到基準桿件的雅可比矩陣。

對式(2)參數(shù)辨識方程使用最小二乘法即可直接得到慣性參數(shù)Φ的辨識結果。一些研究者在此基礎上進行了進一步研究，2015年Ogawa等[13]將式(1)和式(2)結合進行了TORO仿人機器人的參數(shù)辨識實驗；Jovic等[14]2015年提出了一種足式機器人參數(shù)辨識的激勵運動優(yōu)選方法，考慮桿件慣性參數(shù)的實際取值范圍，又于2016年提出了一種基于二次規(guī)劃的分層優(yōu)化參數(shù)辨識方法[15]；Bonnet等[16]對參數(shù)辨識的激勵運動進行參數(shù)化建模，提出了一種能使回歸矩陣列滿秩的激勵軌跡優(yōu)化方法。用該方法進行雙足機器人的慣性參數(shù)辨識時，需要使用運動捕捉設備采集機器人軀干的運動(對應qB及其導數(shù))，并同時記錄機器人各關節(jié)的運動(對應q及其導數(shù))和每個足上完整的6維力信息(對應Fi)，因此難于應用在足底只裝有接觸力傳感器的機器人上。

針對上述問題，本文提出基于足底ZMP的雙足機器人慣性參數(shù)辨識方法，其優(yōu)勢在于：1)與使用式(1)的參數(shù)辨識方法相比；不受關節(jié)摩擦阻尼的影響，能夠得到精度更高的辨識結果；2)與使用式(2)的參數(shù)辨識方法相比，所提出的方法不需要額外的運動捕捉和測力設備，只需要使用機器人自帶的接觸力傳感器就能完成參數(shù)辨識。

本文首先基于足底ZMP數(shù)據(jù)建立雙足機器人慣性參數(shù)辨識的優(yōu)化模型；然后，給出求解此最優(yōu)參數(shù)的算法；最后，對GoRoBoT-II機器人的雙足部分進行參數(shù)辨識實驗，對比所提出的方法和基于關節(jié)力矩的參數(shù)辨識方法(式(1))的結果。

1 基于ZMP數(shù)據(jù)的參數(shù)辨識模型

1.1 雙足機器人的通用模型

機器人第i個桿件的質(zhì)心為Ci，桿件坐標系設為ΣOi-xiyizi，桿件i的慣性參數(shù)共有10個，包括：桿件質(zhì)量mi，桿件系內(nèi)的質(zhì)心位置坐標xi、yi、zi，桿件的慣性矩Ixxi、Iyyi、Izzi、Ixyi、Ixzi、Iyzi，上述參數(shù)可被寫成參數(shù)矢量Φi(i=1,2,…,n)的形式：

Φi=[mixiyiziIxxiIyyiIzziIxyiIxziIyzi]T

(3)

將各桿件的參數(shù)矢量進行組合，可得到機器人的總體參數(shù)矢量：

(4)

其中共含10n個慣性參數(shù)。根據(jù)機器人系統(tǒng)的動力學模型，ZMP的理論位置坐標(x’,y’)為

(5)

(6)

其中，xC、yC、zC是質(zhì)心的位置坐標，F(xiàn)X、FY、FZ是質(zhì)心處慣性力的三軸分量，且

(7)

MX、MY分別是質(zhì)心處慣性力矩的x軸、y軸分量，

(8)

式中：M為測得的機器人總質(zhì)量；PCi和aCi分別為桿件i的質(zhì)心在基坐標系內(nèi)的位置和加速度矢量；pCi為桿件i的質(zhì)心在第i個桿件坐標系內(nèi)的位置矢量，pCi=[xi,yi,zi]T；Pi和Ri分別為ΣOi系在基坐標系內(nèi)的位置矢量和旋轉矩陣；g為重力加速度矢量。

1.2 參數(shù)辨識建模

參數(shù)辨識的基本思想是通過修改參數(shù)標稱值，使理論計算和實測的物理量偏差最小。這里將ZMP的理論坐標(x′,y′)表示成運動狀態(tài)矢量S和參數(shù)矢量Φ的函數(shù)，可定義如下的ZMP偏差函數(shù)：

(9)

式中：Sj為第j個采樣周期測得的S矢量，xj、yj分別為第j個采樣周期測得的ZMP位置x軸和y軸坐標，N為參數(shù)辨識過程中的采樣周期總數(shù)。

參數(shù)識別的優(yōu)化模型可被表示為

Φ*=arg mine(Φ)

c·Φ=M

(10)

式中Φ*為最優(yōu)參數(shù)矢量；Φmin和Φmax分別是由各參數(shù)下限和上限組成的矢量；c為質(zhì)量約束矢量，c=[b1T,b2T, …,bnT]T，其中bi(i=1,2…,n)均是只有第一個元素為1其余元素均為0的10維矢量。

在式(10)的優(yōu)化模型中，第二個約束條件的物理含義為按參數(shù)標稱值計算的機器人總質(zhì)量應等于事先測量的值M。

2 參數(shù)辨識優(yōu)化模型的求解算法

由于式(5)中ZMP的理論位置坐標(x′,y′)無法寫成像式(1)或式(2)那樣的關于參數(shù)矢量Φ的線性形式，因此不能使用最小二乘法進行求解，這里考慮cΦ=M的等式約束，使用如下的迭代法對式(10)中的優(yōu)化模型進行求解：

Φ(k)=Φ(k-1)+[E-c(cTc)-1cT]ΔΦ

(11)

式中上標(k)表示迭代的步數(shù)，E為與Φ同階的單位矩陣，ΔΦ是每次迭代的參數(shù)增量矢量。

一般情況下，增量ΔΦ按牛頓迭代法確定，

ΔΦ=-H-1G

(12)

其中G和H分別為誤差函數(shù)e的梯度矢量和海塞矩陣。當海塞矩陣H奇異時，使用式(13)所示的最速下降法求解ΔΦ，

ΔΦ=-αG

(13)

其中α為學習率(α>0)。上述迭代過程的收斂條件可表示為

‖ΔΦ‖≤ε

(14)

其中，ε為預設的誤差限。綜合式(11)～(14)，圖2給出了上述優(yōu)化模型求解算法的具體計算流程。

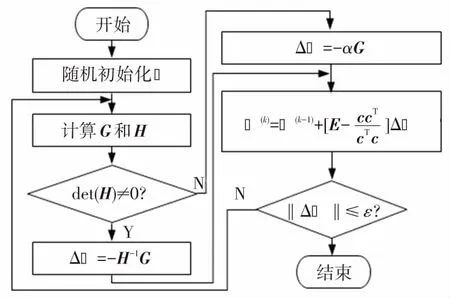
圖2 參數(shù)辨識模型的求解算法流程圖

上述算法中的海塞矩陣H和梯度矢量G分別為

(15)

(16)

(17)

(18)

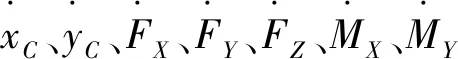
x′和y′關于Φ的二階偏導為

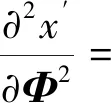
(19)

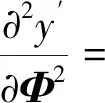
(20)

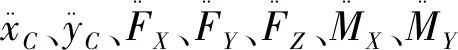
3 參數(shù)辨識的數(shù)據(jù)采集實驗

3.1 待辨識的GoRoBoT-II雙足機器人

本文中待參數(shù)辨識的機器人是作者所在研究室自行研制的GoRoBoT-II型類人猿機器人的雙足部分，該機器人的左右兩腿完全對稱，圖3給出了其照片、機構簡圖、以及腳部拆解后的照片。

圖3 GoRoBoT-II機器人雙足部分的照片和機構簡圖

上述機器人的左右兩腿各有6個轉動關節(jié)，關節(jié)角分別表示為θLi和θRi(i=1,2,…,6)，每只腳掌的四角分別嵌入壓力傳感器，測量機器人與地面接觸的法向力，用于計算機器人的ZMP位置。圖3(b)中m0、m1、m2、m3分別是軀干、大腿、小腿、腳掌桿件的質(zhì)量，lc0、lc1、lc2、lc3分別是上述4種桿件的質(zhì)心位置參數(shù)，圖3(b)中標出的其他參數(shù)均是機器人的機構參數(shù)，其測量值由表1給出。

(b) 足底ZMP點的側向位置坐標曲線

表1 GoRoBoT-II雙足機器人的機構參數(shù)

如圖4所示，本文所使用的GoRoBoT-II型機器人采用上位機+IPM-100運動控制板卡進行關節(jié)位置伺服控制，上位機的運動控制指令通過RS-485網(wǎng)絡發(fā)送到驅(qū)動和控制各關節(jié)電機的IPM-100板卡上，上位機的指令周期為50 ms，IPM-100板卡內(nèi)的位置伺服控制周期為1 ms。

圖4 GoRoBoT-II型雙足機器人的控制系統(tǒng)硬件框圖

考慮機器人的實際情況，從以下3個方面對第1節(jié)中定義的慣性參數(shù)矢量Φ進行了簡化：

1)機器人左右兩腿對應桿件相同，因此待辨識的桿件只有4種，即腳掌、小腿、大腿、軀干；2)由于各桿件均是形狀大體規(guī)則的長方體，這里忽略了其質(zhì)心與桿長方向相垂直的偏移量；3)由于激勵運動需考慮雙足機器人的平衡問題，機器人運動速度一般不快，桿件慣性矩參數(shù)Ixx、Iyy、Izz、Ixy、Ixz、Iyz不能得到充分激勵，因此這些參數(shù)的值將由三維幾何建模的結果進行近似。

經(jīng)簡化，待識別的機器人慣性參數(shù)矢量為Φ=[lc0,lc1,lc2,lc3,m0,m1,m2,m3]T，分別包含軀干、大腿、小腿、腳掌4種桿件的質(zhì)心位置和質(zhì)量。

3.2 參數(shù)辨識的實驗過程

在對圖3所示的機器人進行參數(shù)辨識實驗時，首先令機器人在單腳站立狀態(tài)下做限幅隨機運動，運動樣本由文獻[17]中提出的方法按隨機的參考ZMP軌跡規(guī)劃得到。實驗過程中以50 ms為周期實時采集傳感器數(shù)據(jù)，共進行5次時長約為95 s的實驗，其中1次實驗錄像的截圖如圖5所示。

圖5 一次參數(shù)辨識實驗的視頻截圖

由圖5可見，機器人首先向支撐腳(右腳)偏移質(zhì)心并抬起左腳，之后左腳在空中進行目標位置隨機的平移運動，右腿負責保持機器人平衡，使機器人實際ZMP追蹤隨機的參考ZMP，如此在保證機器人平衡的基礎上，各關節(jié)的角度、角速度、角加速度均呈現(xiàn)連續(xù)變化的隨機波動。

3.3 數(shù)據(jù)采集結果

參數(shù)辨識計算需要以下3類數(shù)據(jù)：

1)機器人的關節(jié)角。由各關節(jié)的伺服電機編碼器反饋和關節(jié)減速比算得，再通過差分運算得到各關節(jié)的角速度和角加速度；2)機器人的關節(jié)力矩。由各關節(jié)伺服電機的電流計算電機轉矩，根據(jù)關節(jié)減速比計算關節(jié)力矩；3)足底ZMP。根據(jù)安裝在機器人腳底的接觸力傳感器反饋，經(jīng)慣性濾波得到ZMP位置。

圖6給出了一次實驗中機器人支撐腿和游腿的關節(jié)角曲線，由于實驗過程中機器人的髖關節(jié)立轉自由度始終處于保持力矩狀態(tài)，靜止不動，因此圖6中沒有給出髖關節(jié)立轉角的曲線。

(a)支撐腿的關節(jié)角曲線 (b)游腿的關節(jié)角曲線

圖7給出了一次實驗中支撐腳4個壓力傳感器采集的原始接觸力曲線，可知壓力原始數(shù)據(jù)中含有高頻擾動信號，不能直接用于參數(shù)辨識計算。

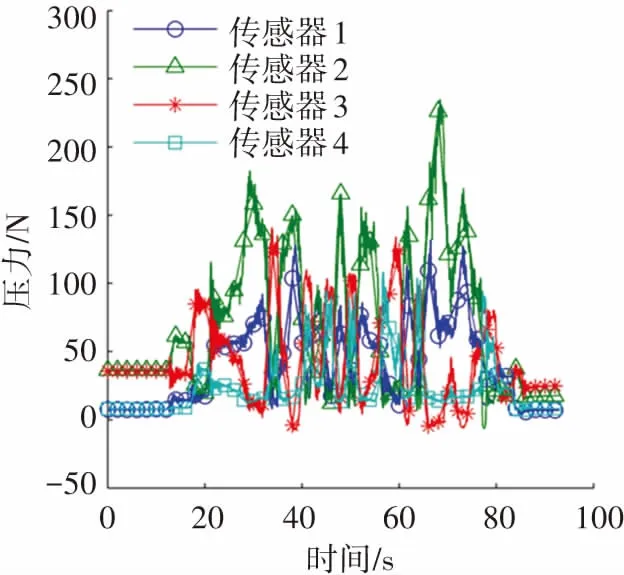
圖7 一次實驗中機器人足底壓力傳感器原始數(shù)據(jù)曲線

使用上述接觸力數(shù)據(jù)計算ZMP位置，得到的x軸(前后向)、y軸(側向)坐標曲線如圖8所示。

由圖8可知，經(jīng)慣性濾波后ZMP坐標的高頻波動顯著減小，且曲線滯后不明顯，因此后續(xù)的參數(shù)辨識計算將使用濾波后的ZMP位置數(shù)據(jù)。

(a)足底ZMP點的前后向位置坐標曲線

圖9(a)、(b)分別給出了一次實驗中機器人支撐腿和游腿的關節(jié)力矩曲線，可以看到，實驗過程中機器人各關節(jié)的轉矩呈現(xiàn)隨機波動的變化規(guī)律，由于游腿的腳掌地面始終與支撐面平行(見圖5)，因此游腿腳踝側偏關節(jié)的力矩始終較小。

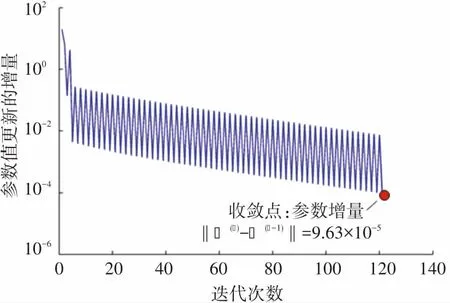
(b) 迭代過程中參數(shù)矢量更新的增量曲線

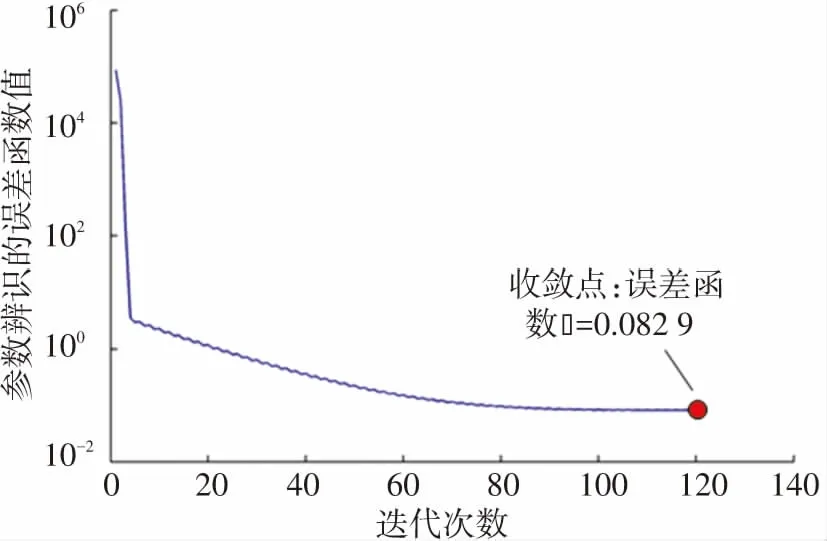
(a) 參數(shù)識別誤差關于迭代次數(shù)的曲線

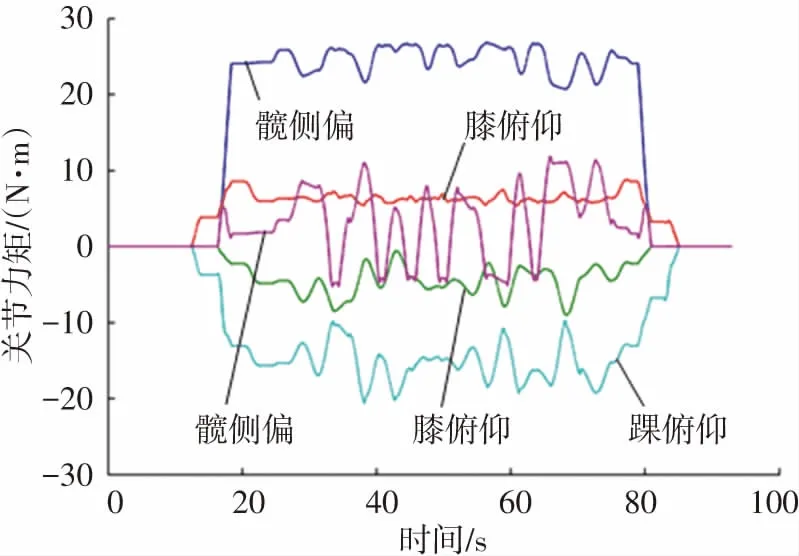
(a) 支撐腿的關節(jié)力矩曲線

(b) 游腿的關節(jié)力矩曲線

4 參數(shù)辨識結果的對比與分析

用第3節(jié)獲得的實驗數(shù)據(jù)，按第2節(jié)給出的參數(shù)辨識求解算法計算最優(yōu)參數(shù)。求解過程中的學習率α由試錯過程確定，初始值設為1，即按照100%的梯度矢量確定參數(shù)矢量Φ的調(diào)整量，然后逐漸減小α的值，直到連續(xù)的3次計算均能收斂于相同結果，此時認為參數(shù)辨識算法達到了穩(wěn)定收斂的結果，在本文中算法穩(wěn)定收斂對應的α值為0.02；確定參數(shù)矢量增量的閾值ε時，考慮到長度參數(shù)和質(zhì)量參數(shù)分別辨識到0.1 mm和0.1 g的精度即能滿足控制要求，因此將ε設為1×10-4。圖10給出了對一次實驗數(shù)據(jù)進行計算得到的誤差函數(shù)(見式(9))和收斂指標(見式(14))，收斂于第121次迭代。

用機器人的關節(jié)力矩進行了參數(shù)辨識計算，計算過程中將機器人的支撐腳作為固定不動的桿件，具體計算方法已在文獻[8-10]中給出，這里不詳細展開。表2分別給出了基于ZMP和基于關節(jié)力矩的參數(shù)辨識結果。包括5次實驗數(shù)據(jù)分別計算得到的參數(shù)均值和標準差，以及由三維幾何建模得到的參數(shù)標稱值。

表2 GoRoBoT-II雙足機器人的參數(shù)識別結果

一般情況下，參數(shù)標稱值的誤差由加工裝配誤差、軟管配線等無法在三維幾何建模中體現(xiàn)的因素引起，因此參數(shù)標稱值與真值的差距不會很大。由表2數(shù)據(jù)可見，基于ZMP的辨識結果更接近三維幾何建模得到的參數(shù)標稱值，且除去參數(shù)m0，基于ZMP的辨識方法在其他7個參數(shù)上均得到了比傳統(tǒng)方法更小的標準差，說明基于ZMP的參數(shù)辨識方法得到的結果好于基于關節(jié)力矩的參數(shù)辨識結果。

表2中參數(shù)m3的辨識結果與三維幾何建模的參數(shù)標稱值偏差較大，是由于m3對應的腳掌桿件處配線相對集中(有2個電機和4個力傳感器的線纜)，對機器人桿件的牽拉作用更強，且所進行的激勵運動中支撐腳的腳掌與地面始終相對靜止，激勵效果弱于其他桿件，因辨識結果的偏差較大。

為進一步比較兩種方法所得結果的優(yōu)劣，在與第3節(jié)相同的條件下，單獨進行了一次機器人的隨機運動實驗，并記錄機器人的關節(jié)運動數(shù)據(jù)和ZMP位置，將表2中給出的參數(shù)均值和新得到的運動數(shù)據(jù)代入機器人的動力學模型，計算了理論ZMP的位置坐標，圖11中給出了不同參數(shù)值對應的理論ZMP與實驗測得的ZMP的距離偏差曲線，其中的水平虛線是不同曲線對應的ZMP偏差均值線，還標出了各曲線的偏差均值。

圖11 不同參數(shù)取值下的理論ZMP與實際ZMP偏差

由圖11可知，參數(shù)標稱值ZMP偏差最大，平均為33.8 mm；基于ZMP的參數(shù)辨識結果的平均ZMP偏差為4.6 mm，好于基于關節(jié)力矩的參數(shù)辨識結果的12.4 mm，說明了所提出的基于ZMP的雙足機器人慣性參數(shù)辨識方法的有效性。

5 結 論

本文僅依靠雙足機器人自帶的傳感器，提出了基于足底ZMP數(shù)據(jù)的機器人慣性參數(shù)辨識方法，并在研究室自主研制的GoRoBoT-II型機器人上進行了慣性參數(shù)辨識的實驗研究，主要結論如下：

1) 建立了基于ZMP數(shù)據(jù)的參數(shù)辨識優(yōu)化模型，并推導了目標函數(shù)的梯度矢量和海塞矩陣，使用最速下降法和牛頓法解決了非線性的參數(shù)辨識模型的優(yōu)化求解問題。

2) 使用GoRoBoT-II型機器人進行了雙腿的慣性參數(shù)辨識實驗，實驗結果表明：與傳統(tǒng)的基于關節(jié)力矩的辨識方法相比，所提出的參數(shù)辨識方法能夠得到更接近于參數(shù)標稱值的辨識結果，在實驗中將將理論ZMP與實際ZMP的平均偏差由12.4 mm降低到了4.6 mm，使平均ZMP偏差縮小了62.9%，得到了更為準確的機器人慣性參數(shù)辨識結果。

綜上，本文所提出的基于ZMP的參數(shù)辨識方法容易實現(xiàn)，且相對于傳統(tǒng)的方法能進一步獲得更準確的辨識結果，為雙足機器人的平衡控制提供了更準確的動力學模型參數(shù)。