臥式加工中心雙驅Z軸裝配體幾何誤差分析

李 響，袁軍堂，汪振華

(南京理工大學 機械工程學院， 南京 210094)

幾何誤差在整個機床生命周期中都影響著機床精度。研究表明，幾何誤差和熱誤差占機床總誤差的65%[1]。因此，有必要建立可靠的誤差模型用于量化各零部件誤差與機床誤差的影響機理，進而辨識關鍵誤差項用于預防和補償。幾十年來，大量研究提出了三角函數模型[2]、Denavit-Hartenberg模型[3]、神經網絡模型[4]、變分運動矩陣[5]、多體系統理論[6]等機床誤差建模方法，然而這些建模方法只能分析各軸運動誤差和整機加工誤差的傳遞關系，無法研究零部件的制造和裝配誤差對單軸裝配精度的影響機理。并且現階段的機床裝配時多依靠工人經驗試湊，公差設計多采用一維/二維尺寸鏈計算法，難以有效表達幾何要素的形位公差特征及其相互間的耦合關系。因此，采用屬于三維公差分析的雅可比旋量模型定量描述各幾何要素表達和傳遞幾何要素在公差域的變動，該模型結合了適合公差表達的旋量模型和適合公差傳遞的雅克比矩陣，已應用于齒輪泵[7]和發動機[8]等裝配過程，而對位置可變的機床雙驅Z軸進給系統的裝配過程研究較少，也沒有考慮雙絲杠誤差的制約關系。

對誤差模型進行敏感性分析能夠量化各誤差項對雙驅Z軸裝配精度的影響權重。目前的敏感性分析包括基于一階偏導數形式[9-10]的局部敏感性分析和包含元效應方法[11]、基于方差方法[12]的全局敏感性分析。其中，基于方差的Sobol法[13-14]能夠計算任意維數輸入參數的敏感性系數及參數間的耦合效應的影響，同時在處理非線性等復雜模型方面具有較大的優越性，因此非常適用于機床幾何誤差敏感性分析并得到廣泛應用[12,15]。然而這些研究只是鑒別出各軸運動誤差對整機精度的敏感性系數，沒有進一步分析零部件在零部件制造和裝配過程中對單軸運動誤差的影響程度，而且只是根據加工條件選擇一個或幾個關鍵位置進行敏感性分析，沒有對整個運動過程進行研究。

本文將雅可比旋量模型拓展到雙驅Z軸裝配體的誤差建模，并考慮雙絲杠的耦合作用和運動條件下的機床雙驅Z軸誤差敏感性分析。首先，利用雅可比旋量理論建立誤差模型；其次，根據裝配流程和幾何誤差的類型和約束條件，調整雅可比旋量模型以適用于雙驅Z軸裝配的誤差建模；然后，對比仿真和實測數據驗證模型的準確性；最后，采用Sobol方法求解不同位置的局部和全局敏感性系數，得到關鍵誤差項。

1 雅可比旋量模型

雅可比旋量模型包含用于描述幾何公差的小位移旋量和用于公差傳遞計算的雅克比矩陣兩部分。

1.1 小位移旋量

剛體運動產生的位移可以用3個平移分量和3個轉動分量表示，當位移值為公差等級或更小時，6個運動分量構成的矢量即為小位移旋量[16](Small Displacement Torsors，SDT)。由于制造誤差和裝配誤差相對于零件尺寸都足夠小，因此可以用小位移旋量表示。其表達式為

(1)

式中：v、u、w分別為x、y、z方向的平移誤差，α、β、γ分別為繞x、y、z軸的角度誤差。

構成零件幾何特征的點、線、面稱為幾何要素(如圓心、軸線、圓柱面等)。幾何要素有多種公差特征(如平面度、直線度、圓柱度等)，決定小位移旋量的參數變化范圍。以直線度和平面度為例，在表1中列出線和面幾何要素的小位移旋量形式。其中，同一幾何要素上可能會有2種或2種以上的組合公差約束，如導軌面的平行度和直線度。此時要根據幾何要素和公差類型，將單個零件上受到多個公差約束的旋量參數進行合并。

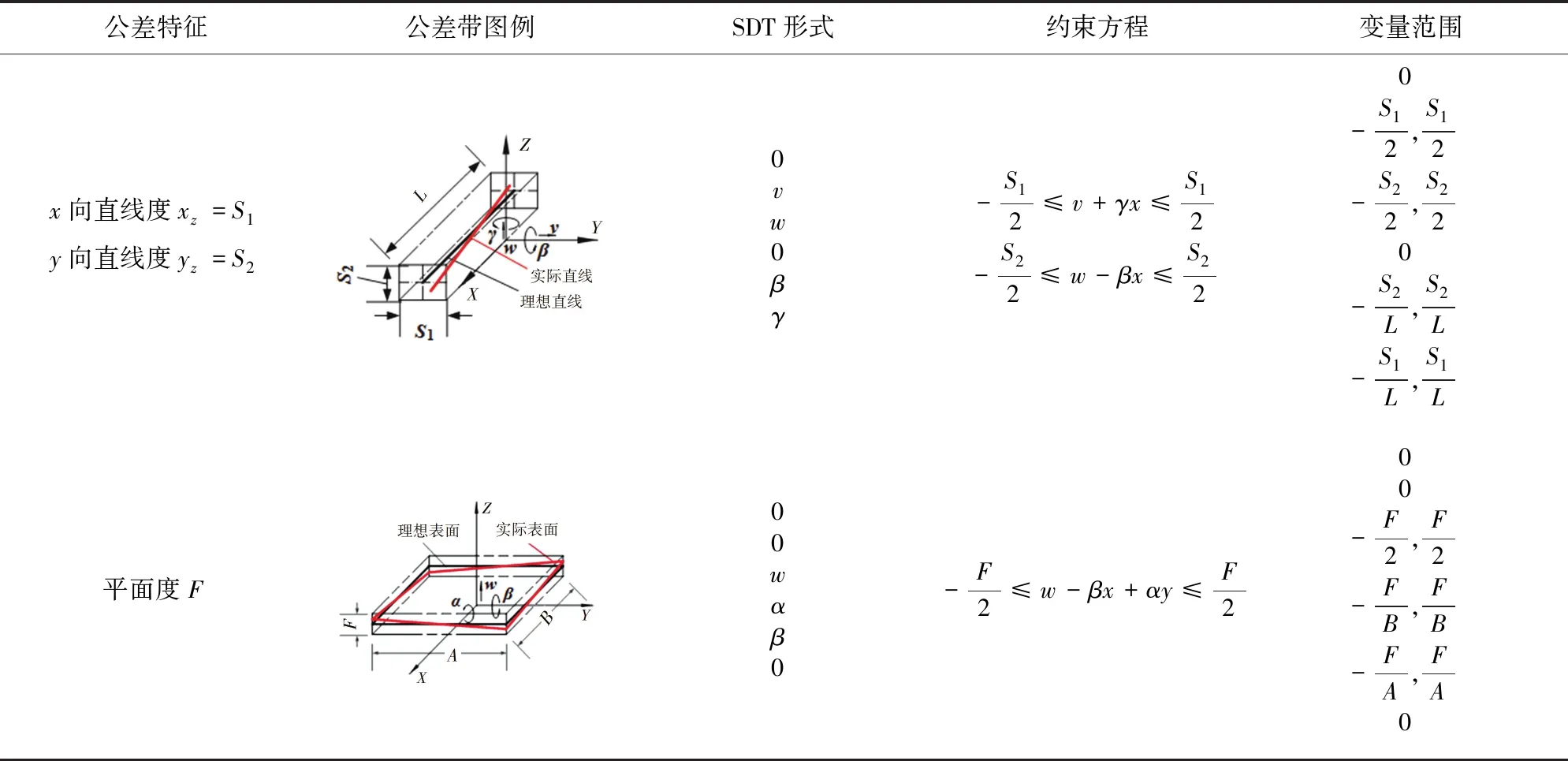
表1 兩種幾何要素的公差要求及其小位移旋量形式

1.2 雅可比矩陣

雅克比矩陣源自于機器人運動學，用于傳遞各關節的位姿和速度[17]。雅克比矩陣分為2個部分，分別用于傳遞幾何要素的平動和轉動。其形式如下：

(2)

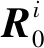
(3)

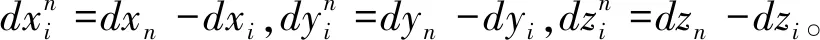
利用雅可比矩陣將各個幾何要素的公差轉換到絕對坐標系中進行累加，得到雅可比旋量模型：

(4)

式中：T為對應幾何要素公差的小位移旋量，E為目標幾何要素公差的小位移旋量。

1.3 統計方法

本文基于蒙特卡洛算法，將旋量中各矢量的變動和約束方程引入到雅克比旋量模型中，實現準確可靠的公差分析。算法流程有6個步驟[18]：

1)建立雅可比旋量模型。根據裝配流程建立各幾何要素的局部坐標系和全局坐標系，建立各要素的雅可比矩陣，根據公差類型確定各要素的幾何特征的旋量表達式。

2)確定各旋量參數的取值范圍。根據公差要求，建立各要素的旋量參數的變動區間和約束方程，并將其代入到雅可比旋量模型中。

3)生成隨機數。假設幾何要素的旋量參數呈正態分布，根據第二步的旋量參數取值范圍和6σ理論，計算各旋量參數的均值和標準差，并生成隨機數。

4)篩選隨機數。利用約束方程篩選第三步生成的隨機數，確保參與計算的隨機數都符合公差要求。

5)模型計算。將符合要求的隨機數代入到雅可比旋量模型中進行計算，重復上述步驟獲取大量數據。

6)結果分析。對仿真結果進行統計分析。

以上就是雅可比旋量模型的統計分析過程。通過旋量模型的統計計算，可以定量預測裝配過程中的誤差變動范圍，為公差分配提供參考。

2 基于雅克比旋量模型的Z軸幾何誤差建模

以MCH63臥式加工中心的雙驅Z軸為例，建立Z軸幾何誤差模型，研究Z軸裝配過程中零部件的制造誤差和裝配誤差對Z軸進給系統幾何誤差的影響機理。

2.1 裝配流程和誤差辨識

Z軸的誤差傳遞過程可由圖1所示的裝配流程確定，詳細尺寸和公差要求列在表2中。從圖1可知，所有零部件安裝在床身上，其中導軌和軸承座安裝于床身上表面。床身作為裝配的基體，本身存在表2所示的制造誤差。

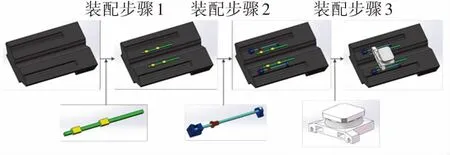
圖1 雙驅Z軸的裝配流程

表2 Z軸進給系統的主要參數

根據Z軸裝配過程，可以看到誤差存在“床身-滑塊”和“床身-螺母”2條傳遞路徑，然后通過安裝工作臺進行耦合。因此，將誤差傳遞分成3個部分——2個誤差子鏈(導軌-滑塊子鏈和絲杠-螺母子鏈)及其在工作臺處的耦合。其裝配實體圖和誤差傳遞路徑如圖2和圖3所示。

圖2 雙驅Z軸進給系統結構

2.2 導軌-滑塊子鏈的誤差傳遞模型

根據圖3，該部件存在4個誤差傳遞鏈，對應4個滑塊。以滑塊A的誤差傳遞過程為例，其他3個滑塊的分析過程類似。導軌-滑塊子鏈的誤差源有FB、SGx、SGy、PRx和PRy，具體含義見表2和圖4。圖4(a)中，符號o、a、b、c分別表示床身的基準位置、床身上的導軌安裝面、導軌1的安裝面和滑塊A的安裝面，對應的雅可比矩陣為Ja、Jab、Jc。為了計算方便，局部坐標系建立在各幾何要素的中心。根據各零件的具體尺寸可以建立該子裝配鏈誤差傳遞的雅克比矩陣JA，見式(5)。

(a) 絲杠螺母安裝尺寸標注

圖3 雙驅Z軸的誤差傳遞示意圖

根據各種公差類型的小位移旋量表達式和對應的公差值，可以計算出幾何要素的誤差變動范圍，表3詳細列出了有關旋量及其約束。其中，導軌面受直線度和平行度公差的共同約束，而形狀公差的公差帶一般要小于方向公差，且此例中的平行度和直線度的公差帶均為兩平行平面所限定的區域。所以，滿足直線度的變量區間也適用于平行度的變量區間。

表3 導軌滑塊裝配鏈的誤差源約束方程及偏差范圍

將雅可比矩陣J_A和表3中對應的旋量代入公式(4)，可推導出由裝配鏈上的各幾何要素公差表示的滑塊A上工作臺安裝面的公差要求，見式(6)。同理可得滑塊B、C、D的公差要求。

(5)

(6)

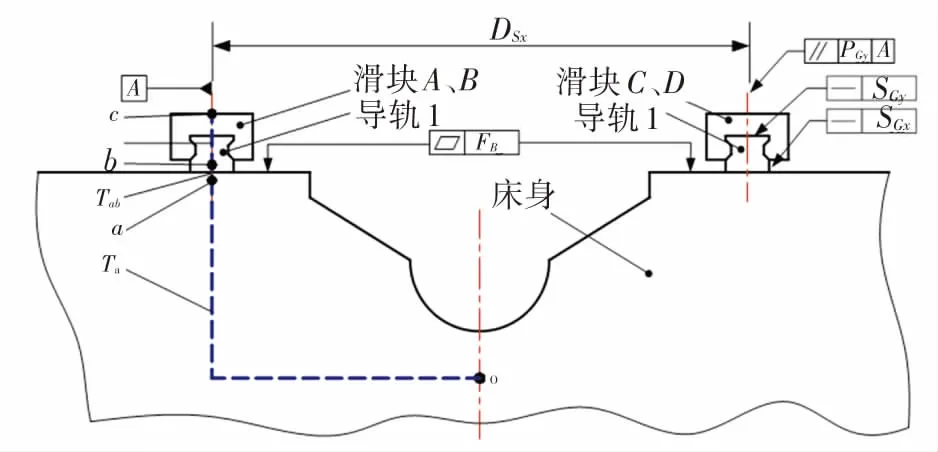
(a)導軌安裝尺寸標注

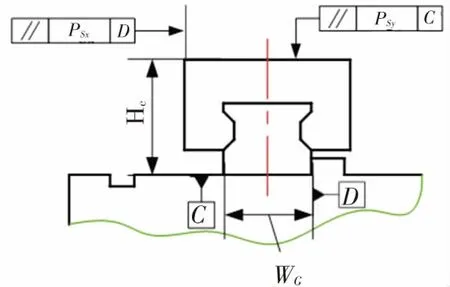
(b)滑塊安裝尺寸標注

2.3 絲杠-螺母子鏈的誤差傳遞模型

在Z軸裝配的誤差鏈中，滾珠絲杠部件的誤差傳遞不同于導軌滑塊部件，但依然可以用雅克比旋量理論進行誤差子鏈的建模。

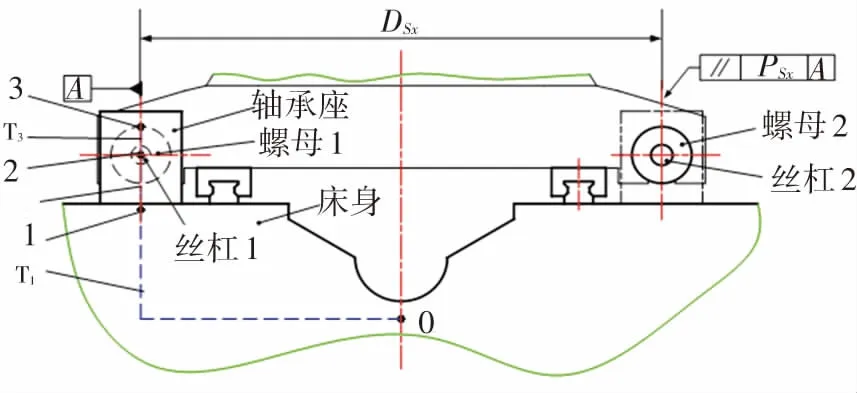
根據圖1的裝配流程，絲杠通過軸端的兩組軸承安裝在床身上，其誤差傳遞路徑如圖5所示。圖5中，代號0、1、2、3分別表示床身的基準位置、床身上的軸承座安裝面、絲杠1的軸承安裝面和螺母1的工作臺安裝面，對應的雅可比矩陣為J1、J12、J3。根據各零件尺寸可以建立該子裝配鏈的誤差傳遞的雅克比矩陣JN1，見式(7)。

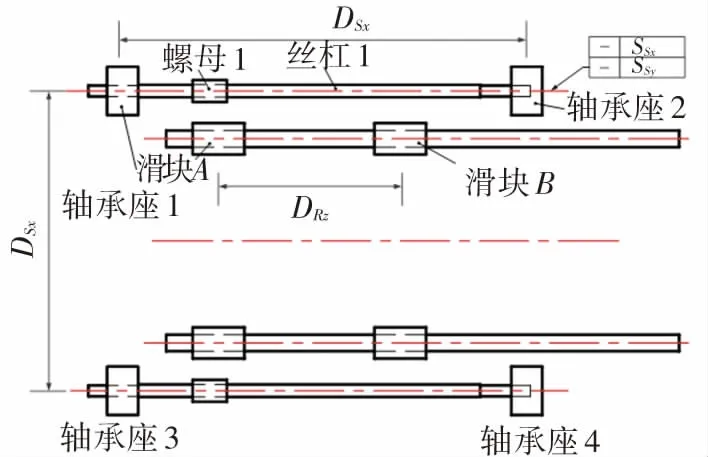
(b) 軸承安裝尺寸標注

裝配過程誤差包括床身、軸承、絲杠、螺母的誤差：床身的制造誤差對絲杠有一定影響；由于支撐軸承的同軸度不可能完全一致，絲桿在安裝過程中存在圖6中的X向和Y向的直線度誤差；絲杠的導程精度也是影響工作臺運動精度的重要原因，一般選擇代表運行距離誤差EP進行研究，如圖7所示。

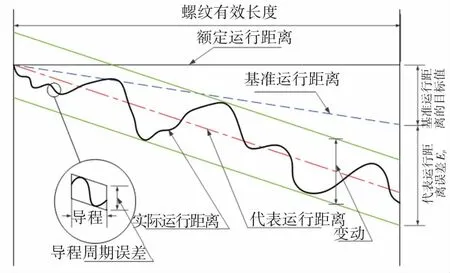
圖7 絲杠導程誤差的累積效應

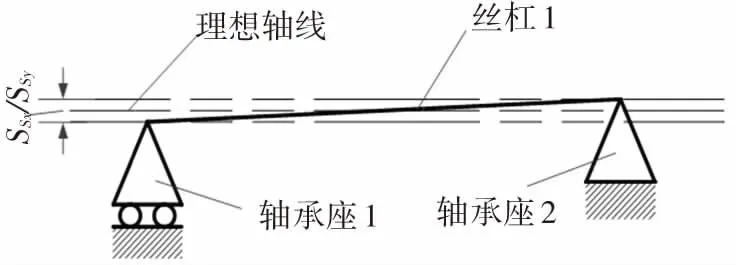
圖6 絲杠安裝的直線度要求

根據上述誤差的定義和取值，可以確定各幾何要素的小位移旋量，見式(8)。將雅可比矩陣JN1和式(8)中對應的旋量代入公式(4)，可得到螺母1的工作臺安裝面的公差要求，該誤差子鏈的雅可比旋量模型為式(9)。

(7)

(8)

(9)

2.4 所有誤差子鏈的誤差耦合

工作臺通過4個滑塊和2個螺母與導軌和絲杠連接。所有誤差子鏈通過安裝工作臺進行耦合，則工作臺各個位置的誤差可以用6個連接支點的變動表示，如圖8所示。

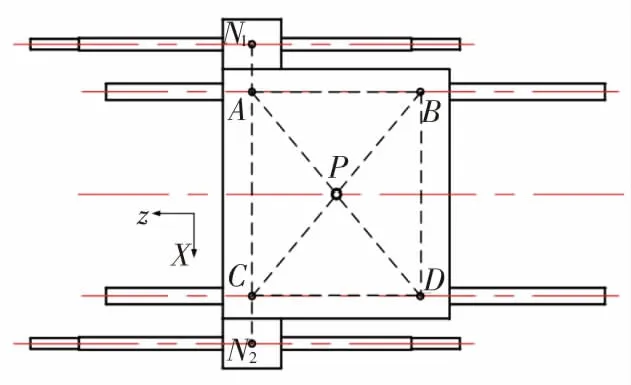
圖8 誤差子鏈的誤差耦合

以4個滑塊的對稱中心為工作臺的參考點。基于前面的分析，進給方向上導軌滑塊無約束，絲杠的螺距誤差為主要影響因素，需與滑塊誤差分別取均值相加，工作臺的平移誤差可以表示為

(10)

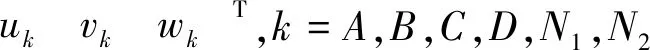
工作臺的轉動誤差可以由滑塊和螺母的相互位置關系求出:

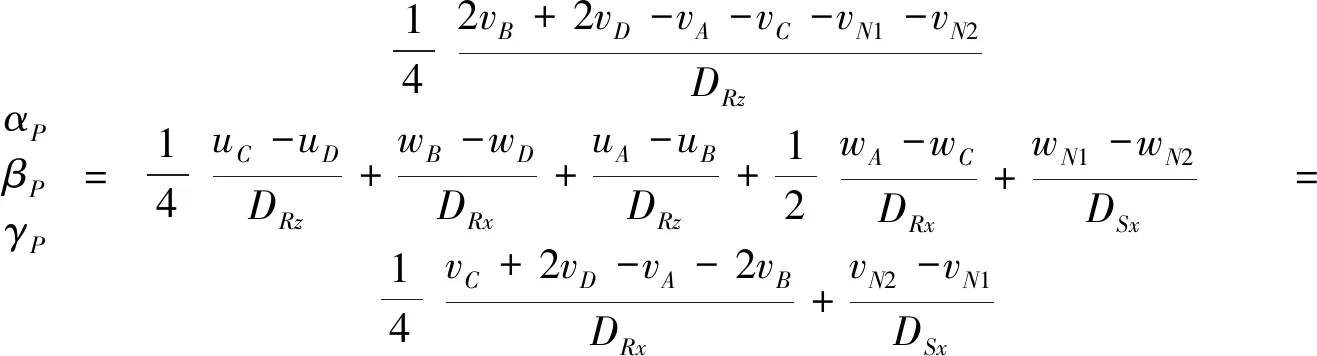
(11)

至此，最終裝配功能需求與絲杠螺母副和導軌滑塊副的幾何要素要求相關聯。

3 幾何誤差模型的有效性驗證

為了驗證雅可比旋量模型的準確性，在此模型的基礎上，通過仿真得到最終誤差的變化范圍。同時，根據國家標準GB/T 20957，需要在機床驗收前測量軸向的定位誤差。因此，選擇Z軸定位誤差用于比較基于雅克比旋量的幾何誤差模型的仿真數據和實際測量數據。此處以南通機床廠生產的10臺同類型臥式加工中心的定位誤差為參照。

Z軸定位誤差的實測數據和仿真數據極值結果列于圖9。從圖中可以看到：所有實測誤差數據均在仿真數據區間內，且誤差變動趨勢相同，模型預測較準確；在坐標值較小時，絲杠的螺距誤差較小，角度誤差對工作定位誤差的影響較大，而仿真與實測數據相差較大，說明螺距誤差為影響定位誤差的主要因素。測量結果表明雅可比旋量法用于誤差分析的實用性，該模型也可以定量地描述機床零部件誤差在裝配過程中的傳遞方式。

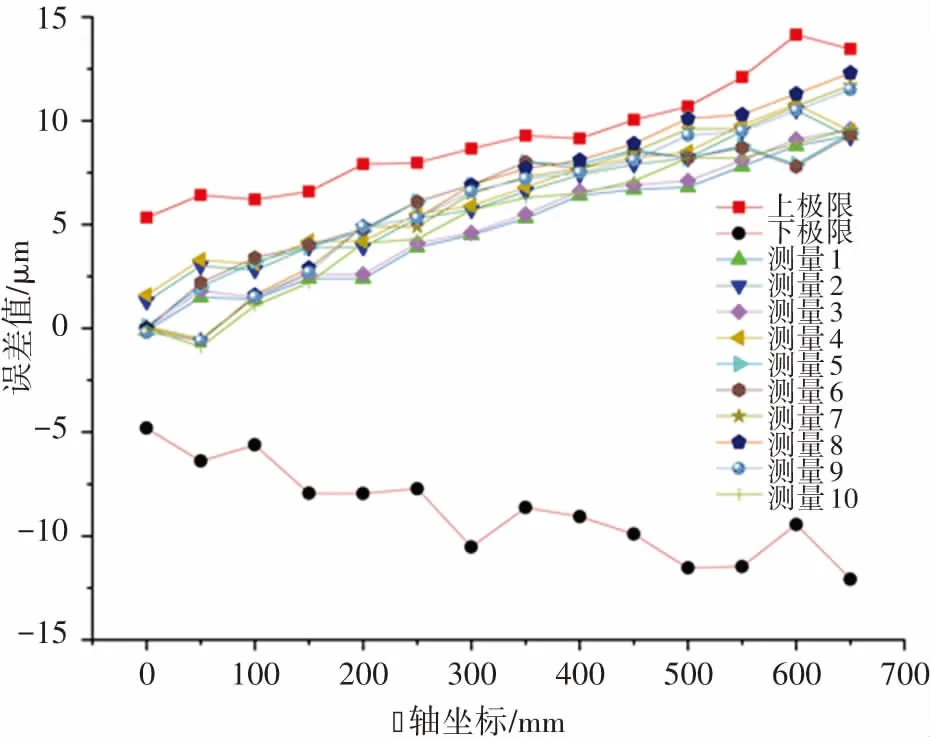
圖9 定位誤差的仿真與測量結果對比

4 Z軸部裝幾何誤差敏感性分析

機床工作臺的運動精度受到零部件幾何誤差耦合而成的空間誤差的影響，每一項誤差對運動精度影響程度不同。為了確定各個誤差元素對運動精度的影響程度，采用Sobol方法進行幾何誤差敏感性分析。采用 Sobol 法進行幾何誤差敏感性分析的基本流程為：

1)構造一個與實際問題或系統相對應的數學模型，數學模型是實現敏感性系數計算的必要基礎；

2)明確各輸入變量的定義域區間，可通過幾何誤差測量及合理縮放得到；

3)對輸入變量的定義域空間進行采樣，并生成相應的采樣矩陣；

4)利用 MATLAB 軟件進行仿真分析及計算，便可求得敏感性系數。

4.1 基于誤差模型的公式推導

首先，利用雅可比旋量模型，最終裝配體的6個誤差分量可以用各零部件幾何要素的公差要求進行表示。具體公式如下:

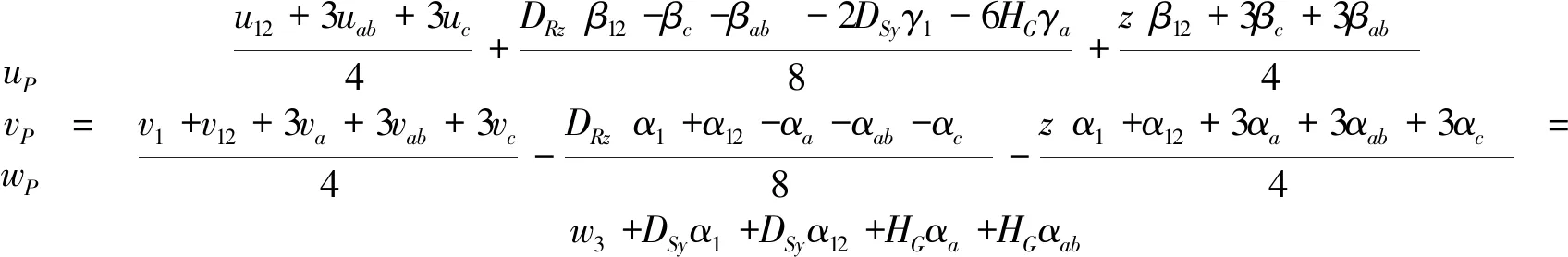
(12)

(13)

式中各參數含義見表2，其中螺距誤差變量Ep的變動范圍定為[-0.02 mm,0.02 mm]，其他變量的變動范圍為[-0.01 mm,0.01 mm]。則進給系統綜合誤差的標量形式為

(14)

4.2 蒙特卡洛估算

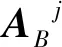
(15)

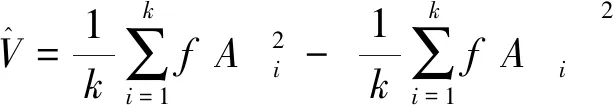
(16)

(17)

(18)

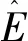
(19)

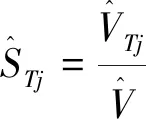
(20)

4.3 敏感性分析結果討論

由進給系統的配置參數可知，Z軸的最大有效行程為650 mm，以50 mm為間隔選取14個位置進行敏感性分析。各位置的誤差項對綜合誤差的敏感性系數如圖10所示，圖中實線空心點代表局部敏感性系數，虛線實心點代表全局敏感性系數。

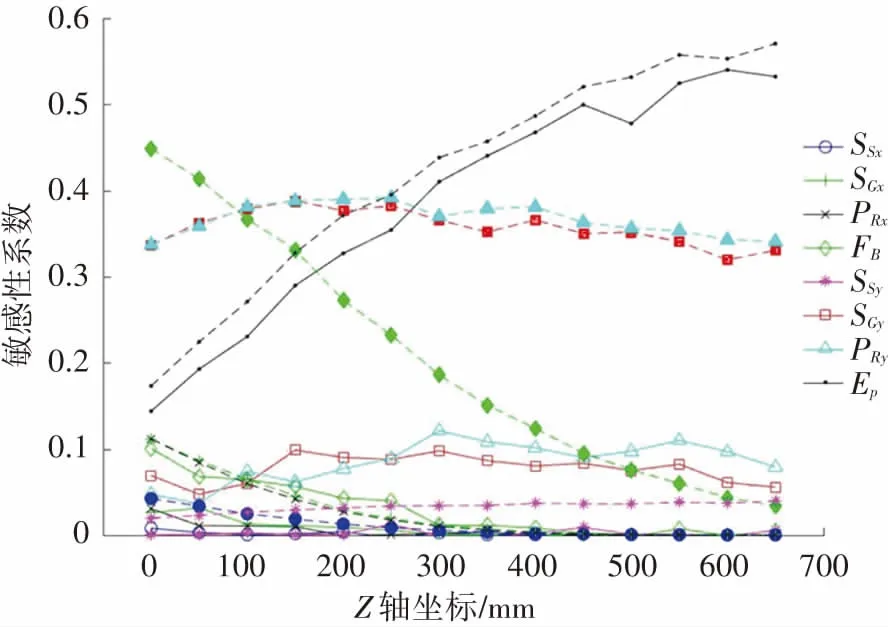
圖10 Z軸變化時各誤差項對綜合誤差的局部和全局敏感性系數

從圖中可以看出：

1)由于絲杠導程誤差的累積效應，代表運行距離誤差Ep的局部和全局敏感性系數隨著運行距離的增加而同步增大，并在300 mm之后成為主要誤差源。說明絲杠導程誤差對工作臺綜合誤差的影響是動態的，需要根據加工位置進行補償。

2)床身平面度FB的敏感性系數在原點處最大且隨著位置的增加而減小，其中全局敏感性系數的降幅遠大于局部敏感性系數。說明在坐標原點即安裝定位基準附近，平面度對綜合誤差的影響較大，由于床身是其他部件的安裝基座，所以由平面度導致的誤差項間的耦合效應較大。

3)導軌Y向的直線度SGy和運行平行度PRy的敏感性系數不隨位置變化，其中全局敏感性系數遠大于局部敏感性系數。說明單個導軌對工作臺綜合誤差的影響程度較小，但安裝到工作臺后，導軌的Y向誤差通過誤差項間的耦合效應對工作臺綜合誤差產生了較大影響。

4)其他誤差項的敏感性系數基本都小于0.1，隨著位置的增加而減小并在300 mm之后趨近于0，只有絲杠Y向的直線度的敏感性系數有小幅度增加。這是由于雙驅進給系統結構的對稱性，導軌和絲杠在X方向上的誤差傳遞到工作臺時會有一定程度的抵消，從而降低X向誤差項的敏感性系數。

5 結 論

1)在明確雙驅進給系統裝配流程的基礎上，將雅可比旋量模型應用于Z軸裝配的誤差傳遞過程。合并平行度和直線度的公差帶區域，確定多種公差約束下的旋量表達式及其變量范圍。對比基于雅可比旋量模型的仿真結果與相似條件下的實測數據，驗證了誤差模型的準確性和適用性。

2)根據誤差模型，采用Sobol方法進行了進給系統的幾何誤差敏感性分析，量化各誤差項對進給系統運動誤差的影響權重，確定了Ep、FB、SGy、PRy是對進給系統運動空間范圍內的運動精度有重要影響的幾何誤差項。其中Ep、FB的敏感性系數在運動過程中會發生變化，需要根據實際加工位置進行動態誤差防止和誤差補償。

3)幾何誤差敏感性分析不但能夠為進給系統在精密設計、制造、裝配調試過程中的幾何誤差指標分配和幾何誤差精度優化提供理論依據，而且能夠在誤差補償階段明確誤差補償順序的優先權。根據敏感性分析結果對重要敏感誤差項進行有針對性的補償和修正可快速地降低重要敏感誤差項對運動精度的影響，可有效地提高進給系統的運動精度。