機床主軸軸向熱誤差一階自回歸建模方法

杜宏洋，陶 濤，侯瑞生，顏宗卓，姜歌東，梅雪松

(1.西安交通大學 機械工程學院，西安 710049；2.機械制造系統工程國家重點實驗室(西安交通大學)，西安 710049；3.智能機器人陜西省重點實驗室(西安交通大學)，西安 710049；4. 河北工程大學 機械與裝備工程學院，河北 邯鄲 056038)

機床誤差主要包括幾何誤差、熱誤差、切削力誤差和控制誤差等。 對于精密加工，熱誤差可以占到總誤差的40%～70%[1-2]。 主軸作為機床的關鍵零部件，也是機床的主要熱源之一。 研究減小主軸熱誤差的方法對提高機床加工精度具有十分重要的意義。 研究表明，熱誤差補償是一種經濟、有效的提高機床精度的方法，而建立高精度、高魯棒性的熱誤差模型是熱誤差補償技術中十分關鍵的環節，很大程度上決定了最終的補償效果。 廣大學者針對主軸熱誤差建模進行了大量卓有成效的研究，提出了多種建模算法，包括多元線性回歸[3-5]、神經網絡[6-9]、支持向量機[10-12]和灰色系統[13-14]等。 但是，模型的精度和魯棒性仍需進一步提高以滿足工廠的實際使用需求。 Yang等[15]指出，前述建模方法魯棒性差的主要原因為機床熱變形是整體溫度場的作用結果，利用少量離散的測溫點建立熱變形的預測模型時會丟失溫度信息，產生圖1所示的“偽滯后”現象，即距離熱源較近位置的溫度變化超前于熱變形，而距離熱源較遠位置的溫度變化滯后于熱變形。 因此，當選取的溫度測點位置不合適時，熱變形ΔL(τ)和溫度t(τ)之間的關系曲線呈現較強的非線性，且在升降溫時不重合，采用ΔL(τ)=f1(t1(τ))或ΔL(τ)=f2(t2(τ))的建模方式難以同時描述升降溫曲線。 楊建國等[16]針對熱變形偽滯后問題指出，對于主軸單端受熱情況，在靠近熱源大概x=0.4L處，主軸熱變形ΔL(τ)和溫度t(τ)呈近似的線性關系且升降溫曲線基本重合。 但是，該結論在實際應用時存在主軸上無法布置溫度傳感器，主軸箱上與主軸0.4L處等效的溫度點不易尋找且受結構限制也可能無法布置溫度傳感器的問題。 目前，多采用時間序列建模算法解決機床熱變形偽滯后問題，將溫度和熱變形的歷史數據作為模型輸入，彌補以離散測溫點替代整體溫度場進行建模時造成的信息缺失[17-19]。 此外，動態神經網絡因包含延遲或反饋環節，也常被用來解決熱變形偽滯后問題[20]。 時間序列算法和動態神經網絡的應用對熱誤差模型的精度和魯棒性的提高起到了一定的效果，但是也引入了新的問題。 如在應用時間序列建模時沒有統一的定階方法，并且模型系數完全由試驗數據確定，不具備物理意義，而動態神經網絡需要設計更符合偽滯后效應的反饋單元結構[21]。 Fraser等[22]指出，熱誤差模型的數學形式不具備物理意義也是影響模型精度和魯棒性的重要因素。 Hou等[23]和顏宗卓等[24]針對該問題，提出了將理論建模與經驗建模相結合的方法：首先，將主軸箱熱傳導簡化為半無限大平板傳熱，計算得到其溫度場和熱變形的解析表達式；然后，通過一定的數學簡化得到主軸箱熱變形的模型形式；最后，利用實驗獲取模型系數。 這種建模方法提高了模型的物理支持，但是推導過程中的數學簡化在一定程度上降低了模型的精度。

為了降低偽滯后效應對熱誤差模型精度和魯棒性的影響，同時為了提高模型的物理意義，本文將主軸簡化為一維桿件，從傳熱學的角度推導出一維桿在變化熱源條件下熱變形的一階自回歸模型。 通過理論推導確定了自回歸模型階數為一階，并根據模型系數的表達式確定了系數與主軸物理特性、自回歸模型時間間隔以及熱源條件的關系。 整個推導過程不存在數學簡化，僅僅是進行形式變換，因此模型精度更高。

1 主軸熱變形計算及一階自回歸模型推導

1.1 主軸溫度場和熱變形理論求解

將主軸簡化為圖1(a)所示的一維桿結構，在左端施加熱源，通過圓柱面進行對流散熱，其導熱微分方程和定解條件為：

(1)

式中：t(x,τ)為一維桿溫度分布函數(℃)，x為一維桿軸向坐標(m)，τ為時間(s)，h為表面傳熱系數(W/(m2·K))，λ為導熱系數(W/(m·K))，R為一維桿半徑(m)，tam為環境溫度(℃)，ρ為一維桿密度(kg/m3)，c為比熱容(J/(kg·℃))，t(x,0)為初始時刻一維桿的溫度場分布(℃)，f(x)為任意函數，L為一維桿長度(m)，q為熱流密度(W/m2)。

引入過余溫度θ(x,τ):

θ(x,τ)=t(x,τ)-tam

(2)

并且設：

a=λ/(ρc),b=2h/(ρcR),θ0(x)=f(x)-tam

(3)

將式(2)和式(3)代入式(1)可得：

(4)

對式(4)進行求解可得溫度場分布：

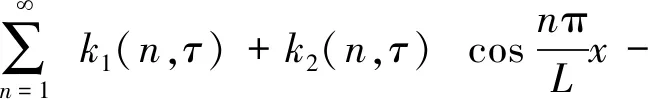
(5)

式中：

(6)

(7)

從式(5)中可以看出，當初始過余溫度θ0(x)=0時，一維桿位置x在τ時刻的溫升與熱流密度q成正比。 此推論在后續將被用于估計不同轉速下主軸受熱的熱流密度之間的關系。 一維桿的熱變形為

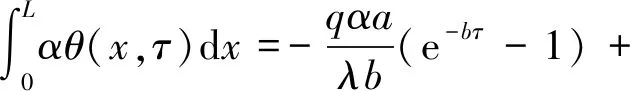
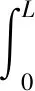
(8)

式中：ΔL(τ)為一維桿的軸向熱膨脹量(m)，α為熱膨脹系數(1/K)。

1.2 主軸熱變形一階自回歸模型推導

(9)

2)在mΔτ時刻一維桿左端熱流密度變為q2，此時視為第二階段的初始時刻，初始溫度為

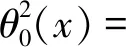
(10)

因此，第二階段熱變形：

(11)

由上述推導可知，一維桿熱變形可表述為

ΔL(nΔτ)=C1ΔL((n-1)Δτ)+C2(q)

(12)

C1=e-bΔτ

(13)

C2(q)=-qαa/(λb)(e-bΔτ-1)

(14)

由式(13)和式(14)中可看出，C1與一維桿物理特性及時間間隔Δτ相關，而一維桿物理特性通常可以認為是固定不變的，因此在時間間隔選定后，C1可視為常數。C2(q)與一維桿物理特性、時間間隔及熱流密度相關，在一維桿物理特性和時間間隔確定的條件下，系數C2與熱流密度q成正比。

主軸在實際使用時為三維傳熱，而且結構比一維桿要復雜很多，散熱系數等邊界條件也不易精確確定。 因此本節的推導只是為主軸熱誤差提供一種建模的數學形式，并為不同轉速(熱流密度)下模型系數的修正提供一定的理論依據，而模型的實際系數需要根據實驗測得的數據進行確定。

2 一階自回歸模型的有限元仿真

對一階自回歸模型進行有限元仿真。 取有限元單元類型為brick 20node 226，一維桿R=0.1 m，長度L=0.8 m，導熱系數λ=50 W/(m·K)，密度ρ=7 850 kg/m3，比熱容c=460 J/(kg·℃)，彈性模量E=206 GPa，泊松比為0.3，熱膨脹系數為12×10-6/K，表面傳熱系數h=55 W/(m2·K)，設定環境溫度、桿的初始溫度以及參考溫度均為20 ℃。

為一維桿施加熱流密度時以工廠典型的零件加工過程為參考，即上午加工4.0 h，中午停機1.5 h，下午加工4.0 h，最后停機14.5 h完成一天的生產過程。 另外，機床在加工不同的零件時，加工工藝的不同導致主軸受熱的熱流密度不同。 因此，進行兩組計算，分別取升溫時的熱流密度為2 000 W/m2和3 000 W/m2，降溫時的熱流密度為0。 設自回歸模型時間間隔Δτ=30 s，則計算可得C1=e-bΔτ≈0.990 9，C2(2000)≈0.198 5，C2(3 000)≈0.297 7，C2(0)=0。

利用得到的一階自回歸模型系數計算一維桿熱變形，并與有限元仿真數據進行對比，結果如圖2和圖3所示。 可以看出,前述一階自回歸建模方法可有效描述一維桿在變化熱源條件下的熱變形規律，但是也存在誤差：一方面是由于在進行有限元在計算時并不是單純的一維傳熱，還存在徑向的熱傳導與變形；另一方面是數值計算方法本身存在的誤差。

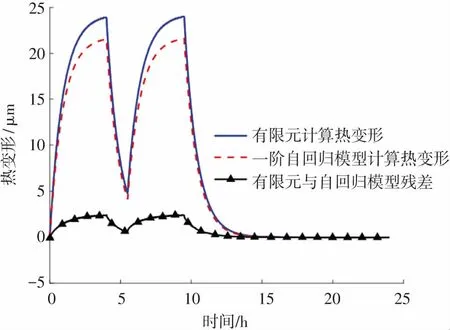
圖2 有限元與自回歸模型計算熱變形對比(q=2 000 W/m2)

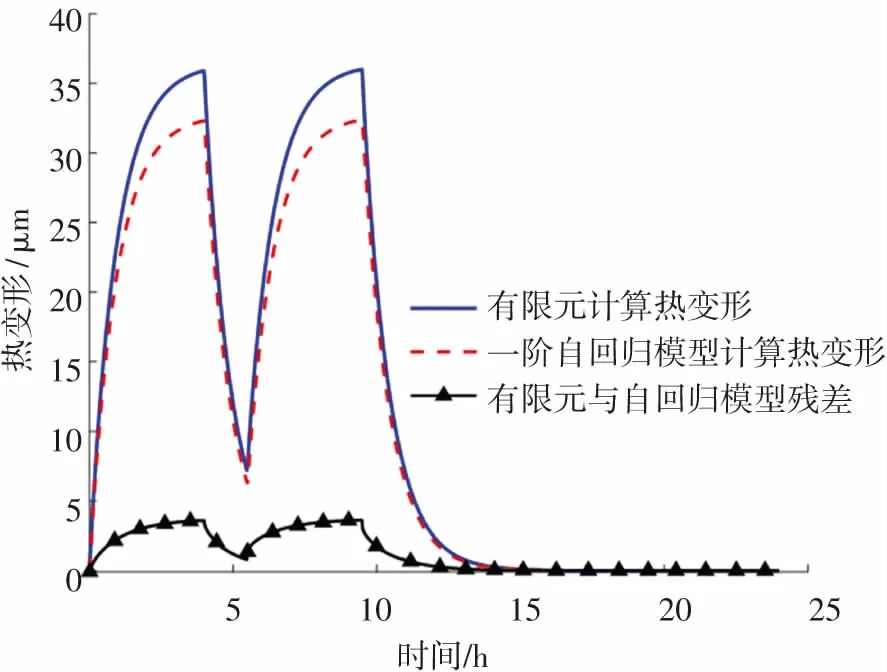
圖3 有限元與自回歸模型計算熱變形對比(q=3 000W/m2)

3 一階自回歸模型實驗驗證

3.1 T65車床Z向熱誤差一階自回歸建模

在實際使用時機械主軸采用雙端軸承支撐結構，即為雙端受熱。 楊建國等[16]經研究指出，一維桿在單端熱源條件下的熱變形規律可以推廣至雙端熱源。 因此，第1、2節的分析結果可應用至實際主軸的熱變形。 本研究以海德曼T65車床為對象，進行主軸熱伸長一階自回歸建模方法的驗證。 溫度測量采用PT100溫度傳感器，量程為-20～100 ℃，精度為A級；熱變形測量采用合肥置信WD502A型電渦流傳感器，量程為2 mm，非線性誤差為0.5%，分辨率為0.2 μm。 溫度點布置見圖4(a)。 實驗時，將渦流傳感器調整至量程中部以減少非線性誤差，并采用連續啟停的方式，以60 s為一個周期。 在一個周期內主軸運轉55 s后準停在某一固定位置5 s用于位移數據的采集。 這種測量方式可以減少主軸轉動時的跳動帶來的誤差以及檢棒自身的制造誤差。

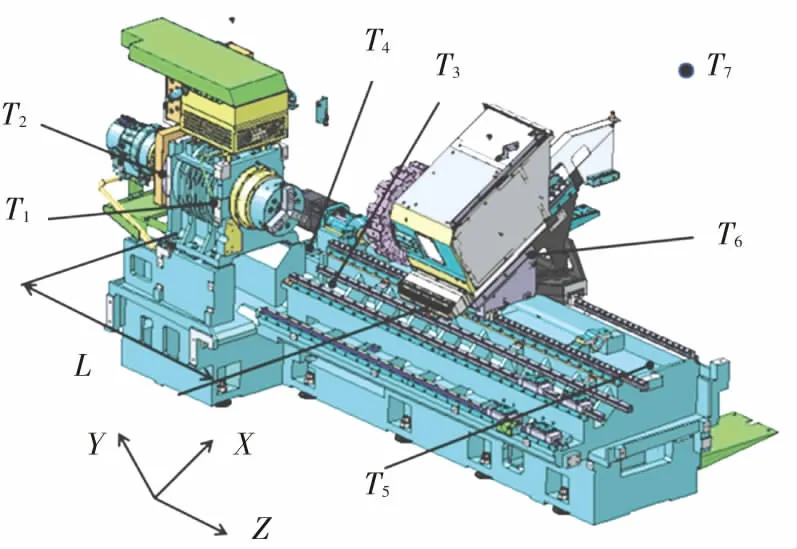
(a)溫度傳感器布置

(b)機床X和Z向熱變形測量

本研究進行了3組實驗，以第1組實驗數據進行建模，并以另外兩組實驗數據進行模型魯棒性驗證。 3組實驗中主軸均運行12 h然后停機降溫12 h，轉速分別為2 000 、1 000 和1 500 r/min，測量結果如圖5所示。

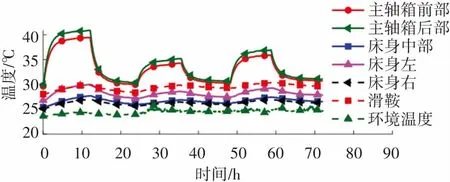
(a)溫度曲線

(b)熱變形曲線

由圖5可看出，在轉速2 000 r/min的條件下，主軸軸承位置溫升達到10 ℃以上，會使主軸箱在豎直方向以及主軸在軸向產生較大的熱變形，從而影響機床的加工精度。 床身整體溫升較小，在靠近主軸箱處溫升稍大，但是因為床身尺寸較大，其熱變形對加工精度的影響不可忽略。 由熱變形曲線可知，機床在X向熱變形較小，基本控制在10 μm以內，Z向熱變形較大，當主軸轉速為2 000 r/min時，Z向熱變形達到30 μm。 本文依據一維桿軸向熱變形規律推導得到一階自回歸模型，而且機床X向熱誤差基本滿足加工要求，因此本文主要針對機床Z向熱變形進行模型驗證及補償。

張老師啊，楊校長使勁咽了口唾沫說，李書記今天來學校找我談過了。他的意思是，先讓你忙一段家里的事，教學的工作先放一放。不是，不是那意思，你別誤會。我是想你如果忙起來，顧得了這頭，顧不了那頭。要不你先把家里的事忙完，再盡早回來上課。

由機床結構分析可知，機床Z向熱變形主要受床身和主軸的熱膨脹影響，其中床身熱膨脹使傳感器架和檢棒之間的距離變大，而主軸熱膨脹使傳感器架和檢棒之間的距離變小。 在機床升溫初始階段，主軸溫升較快，其熱變形占主導地位；升溫一段時間后，主軸溫升變緩，床身的熱變形占主導地位。 這就是機床Z向熱變形曲線先迅速變小，一段時間后變平緩甚至增大的原因。 因此機床Z向熱誤差為

ΔLZ=ΔLbed-ΔLsp

(15)

式中：ΔLbed為床身Z向熱變形，ΔLsp為主軸Z向熱變形。

床身的熱膨脹變形為

ΔLbed=α*L*ΔT3

(16)

式中：L為主軸箱后部至X軸絲杠位置的床身長度，約為1.2 m，如圖4(a)中所示，α為鑄鐵的熱膨脹系數，取10×10-6/℃，ΔT3為床身中部位置的溫升，近似視為床身的平均溫升。

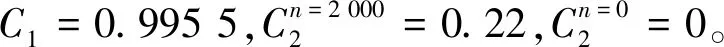
綜上所述，基于一階自回歸方法得到的模型為

(17)

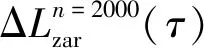
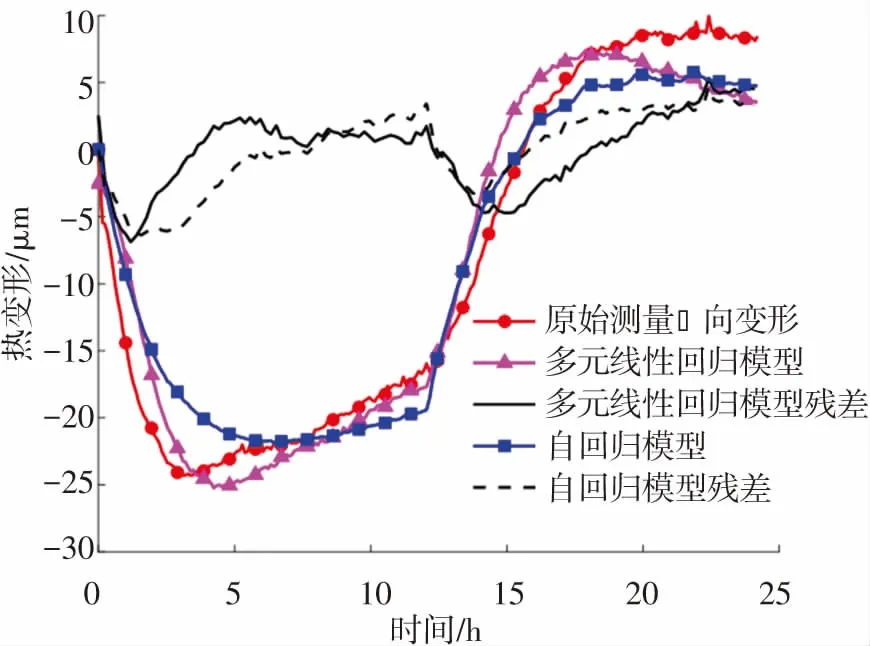
圖6 機床Z向熱誤差建模(n=2 000 r/min)

ΔLzmlr=-2.544 4-1.411 8ΔT1+0.354 3ΔT2+26.417 6ΔT3-20.741 0ΔT4

(18)

從圖6的曲線形式可初步判斷出自回歸模型的殘差不滿足白噪聲的特性。 為進一步判斷，本文對自回歸模型的殘差進行LB檢驗，構造的統計量為

(19)

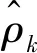
表1 自回歸模型殘差的LB檢驗

由圖6可知，一階自回歸建模方法與多元線性回歸建模方法對于建模數據具有相近的擬合精度，擬合殘差基本控制在±5 μm。 但是，多元線性回歸模型依據殘差平方和最小標準對數據進行擬合，模型系數缺乏物理意義。 從式(18)中可以看出多元線性回歸模型床身的系數偏大，該模型對床身溫度的波動較為敏感。

3.2 一階自回歸模型魯棒性驗證

為驗證一階自回歸模型的魯棒性，用前述建立的模型預測主軸轉速為1 000、1 500 r/min時機床Z向熱變形，并與多元線性回歸模型進行對比。

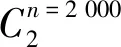
表2 不同轉速下主軸箱后端在前100 min內的溫升

由表2可得：

(20)

(21)

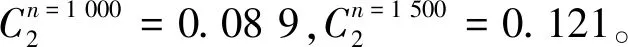
(22)

(23)

利用求得的自回歸模型預測機床在轉速為1 000 、1 500 r/min時Z向熱變形，并與式(18)的多元線性回歸模型的結果進行對比，如圖7所示。

從圖7中可以看出，在主軸轉速為1 000 r/min時，一階自回歸模型預測殘差為4 μm，預測精度為69%；多元線性回歸模型的預測殘差為6 μm，預測精度為54%。 在主軸轉速為1 500 r/min時，一階自回歸模型預測殘差為5 μm，預測精度為70%；多元線性回歸模型預測殘差為9 μm，預測精度為47%。 因此，一階自回歸模型對于非建模工況具有更好的精度保持性。

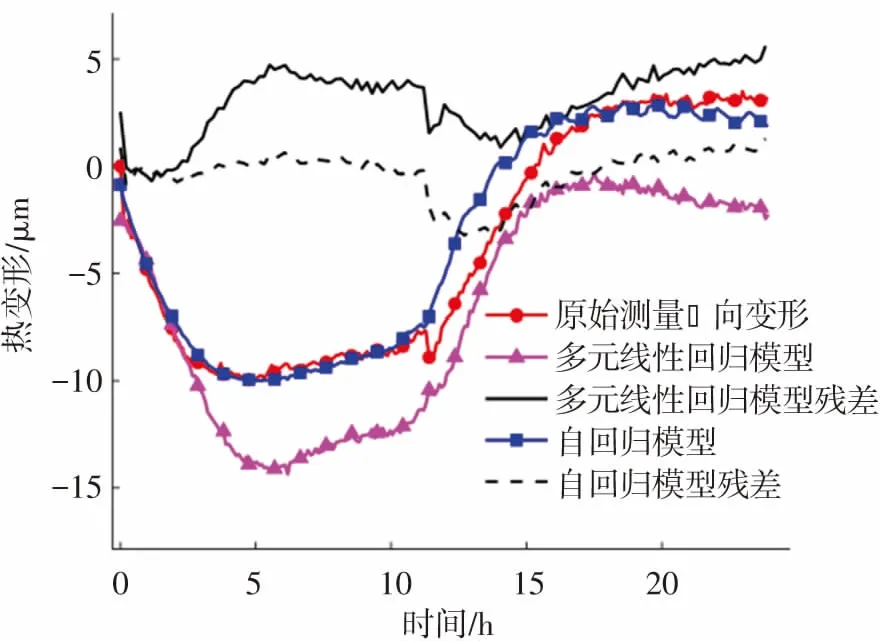
(a)n=1 000 r/min

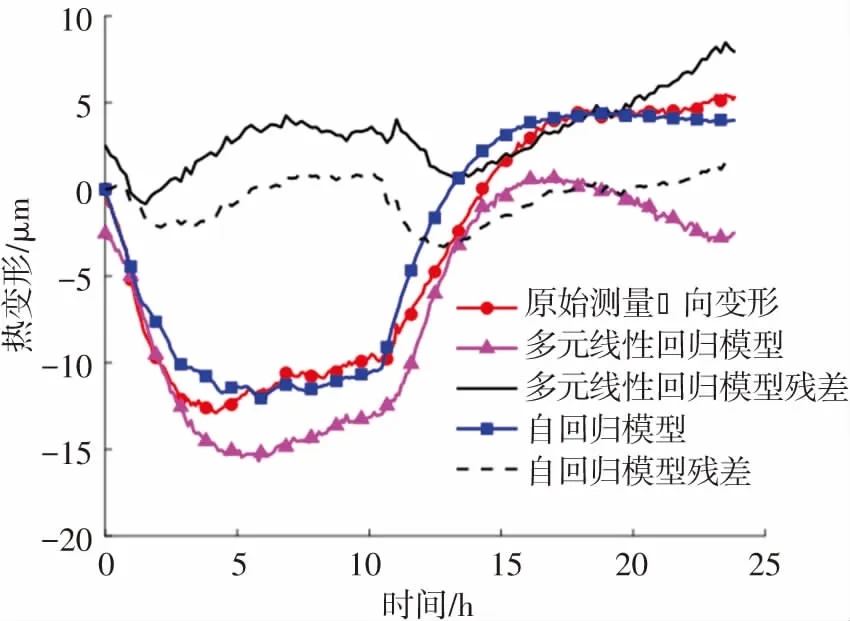
(b)n=1 500 r/min

3.3 機床Z向熱誤差補償

利用前述分析結果對T65機床進行熱誤差補償。 本實驗所用T65機床采用西門子828D數控系統，具有專用的熱誤差補償接口，西門子系統將熱誤差補償值分為與位置無關的補償值和與位置相關的補償值，其補償原理為

ΔKZ=K0(T)+tanβ(T)×(PZ-P0)

(24)

式中：ΔKZ為位置PZ上的溫度補償值，K0(T)為與位置無關的補償值，PZ為軸的實際位置，P0為軸的參考位置，tanβ(T)為與位置相關的溫度補償的系數。

本文只考慮機床Z向與位置無關的熱誤差。 利用自主開發的溫度補償模塊采集溫度數據，并將式(17)建立的一階自回歸熱誤差模型寫入模塊內部計算熱誤差補償量，通過將模塊并口與西門子PP 72/48D 2/2A PN外設模塊的X111口連接，將溫度和補償量數據傳輸至PLC，編寫PLC程序將補償量寫至Z軸的SD43900參數中。 為實現熱誤差補償，需將參數MD32750設定為1，即與位置無關的溫度補償功能生效，通過“垂度補償+溫度補償”參數可實時查看生效的補償值。

實施熱誤差補償后，機床主軸轉速為2 000 r/min 時Z向熱變形測量結果見圖 8。 從圖8中可以看出，機床Z向熱誤差控制在10 μm內，滿足工廠的實際使用需求，從而驗證了一階自回歸模型的有效性。

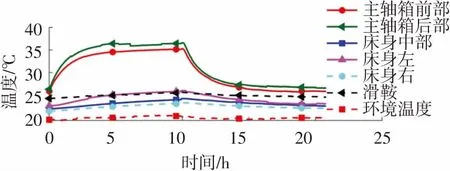
(a)溫度曲線

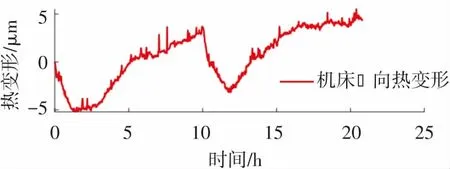
(b)熱變形曲線

4 結 論

本文提出了變熱源條件下主軸軸向熱變形的一階自回歸建模方法，并通過有限元仿真及實驗驗證了模型的有效性，主要結論如下：

1)一階自回歸建模形式符合主軸在變熱源條件下的物理變形規律，建模魯棒性比多元線性回歸更高，并且不受偽滯后效應的影響。

2)自回歸模型系數C1是與主軸物理特性及時間間隔Δτ相關的常數；C2(q)是與主軸物理特性、時間間隔及熱流密度相關的系數，當主軸轉速不同時，C2(q)需要依據熱流密度進行修正。

本文提出的主軸熱變形一階自回歸建模方法適用于機床環境溫度基本恒定的情況。 當車間環境溫度波動較大時，機床溫度場分布和熱變形規律會發生較大改變，從而影響熱誤差模型精度。 如何使模型適應環境溫度的變化還需進一步研究。