基于MATLAB的小波閾值法在信號(hào)降噪中的應(yīng)用研究
楊天晴 楊靜宗 付 蕊 吳麗玫
(保山學(xué)院信息學(xué)院,云南 保山 678000)
在我們生活的環(huán)境中,噪聲無處不在。一方面,由于受噪聲和干擾的污染,導(dǎo)致由采樣信號(hào)辨識(shí)得到的系統(tǒng)模型存在偏差妨礙了系統(tǒng)控制精度的提高[1]。另一方面,含噪信號(hào)對(duì)我們的工作和生活造成了很多負(fù)面影響。語音信號(hào)降噪的實(shí)現(xiàn)將會(huì)提高辦公效率,為我們進(jìn)行信息交流營(yíng)造一個(gè)舒適的聽覺環(huán)境。在語音信號(hào)降噪領(lǐng)域中,傳統(tǒng)的方法有濾波器法、小波變換法、小波閾值法[2?4],其中,韓長(zhǎng)軍[2]運(yùn)用IIR和IFR兩種濾波器對(duì)語音信號(hào)進(jìn)行降噪,該方法能夠?qū)崿F(xiàn)對(duì)夾雜噪聲的語音信號(hào)進(jìn)行有效成分的提取,但是只能提取微弱語音信號(hào),語音信號(hào)和噪聲信號(hào)頻譜分析要求高工作量大,且降噪效果不明顯。唐玲和程建[3]采用小波分析對(duì)語音信號(hào)進(jìn)行特征提取,選取適當(dāng)?shù)男〔ㄋ惴ㄟM(jìn)行語音信號(hào)降噪,該方法能夠消除一些噪聲,但效果不是太明顯。自1995年D.L.Donoho[4]提出小波閾值降噪方法后,很多學(xué)者就把該方法應(yīng)用到語音信號(hào)的降噪中去,結(jié)果表明小波閾值法和以上兩種方法降噪相比,降噪效果提高了許多。但是,這種傳統(tǒng)的方法,閾值單一,在降噪聲的同時(shí),造成語音信號(hào)失真且信號(hào)容易震蕩,降噪效果并不是最優(yōu)的。除此之外,小波基的合理選取、層數(shù)的劃分、閾值的估計(jì)等問題一直是一個(gè)難點(diǎn)。于是,張雪等采用EEMD聯(lián)合能量熵及小波閾值的語音降噪方法[5],該方法從根本上克服了小波分解中需要預(yù)先設(shè)定小波基和分解層數(shù)的問題,也達(dá)成了良好的抑制噪聲目的,但信號(hào)容易失真。通過分析現(xiàn)有研究成果發(fā)現(xiàn),目前信號(hào)處理方法往往存在適用范圍小、參數(shù)選取困難、降噪效果差、信號(hào)失真率高等問題。針對(duì)以上問題,以MATLAB仿真軟件為仿真實(shí)驗(yàn)平臺(tái),采用EEMD結(jié)合小波閾值法和單純的小波閾值法對(duì)含噪語音信號(hào)進(jìn)行降噪。比較這兩種方法以及其中的硬閾值、軟閾值、硬軟閾值折衷這三種閾值函數(shù)的降噪效果。
1 算法的相關(guān)基本原理理論
1.1 小波變換
小波變換是一種信號(hào)的時(shí)間—尺度分析方法,是一種時(shí)間窗和頻率窗都可以改變的時(shí)域局部化分析方法,經(jīng)過伸縮和平移運(yùn)算功能對(duì)函數(shù)或信號(hào)進(jìn)行多標(biāo)準(zhǔn)細(xì)化剖析,達(dá)到在低頻部分具有較高的頻率分辨率和較低的時(shí)間分辨率,在高頻部分則與之相反,能夠自動(dòng)適應(yīng)時(shí)頻信號(hào)分析的要求,任何信號(hào)細(xì)節(jié)都不會(huì)被忽視,因此被譽(yù)為“數(shù)學(xué)顯微鏡”[6]。小波分析的這樣特點(diǎn)與語音信號(hào)的“短時(shí)平穩(wěn)”特點(diǎn)剛好吻合,因此小波分析在語音信號(hào)處理中得到十分廣泛應(yīng)用。
這里所說的小波,單從從字面意思去理解就是指小的波,即ψ(t)表示小波,滿足:

小波變換是一個(gè)平方可積函數(shù)f(t)∈L2(R)與一組在時(shí)域和頻域上都具備較好局部性質(zhì)的小波基ψ(t)的內(nèi)積,則f(t)的小波變換定義[7][8]為:
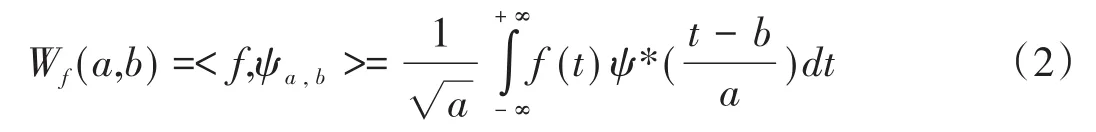
式中,<*,*>表示內(nèi)積;a>0為尺度因子,b為位移因子;*表示共軛復(fù)數(shù);ψa,b(t)為:
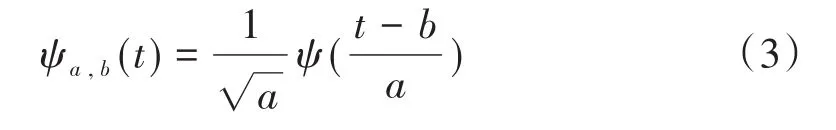
式中ψa,b(t)是母小波經(jīng)過位移和伸縮所產(chǎn)生的一個(gè)小波序列,稱為小波基函數(shù)或簡(jiǎn)稱小波基。
小波變換具低熵性、多分辨率特性、去相關(guān)性、選基靈活性等特點(diǎn),其在時(shí)域和頻域上都具有表征信號(hào)部分特征的能力,因此對(duì)檢測(cè)信號(hào)的瞬態(tài)或奇異點(diǎn)有利,可以覆蓋整個(gè)頻域,實(shí)現(xiàn)算法簡(jiǎn)單且執(zhí)行速度較快且具有“變焦”的特性,在低頻段可以用寬分析窗口,在高頻段可以用窄分析窗口[8]。
1.2 小波降噪方法
隨著小波理論研究的不斷發(fā)展進(jìn)步,它的應(yīng)用領(lǐng)域也越來越廣泛,其中利用小波變換進(jìn)行信號(hào)降噪及重構(gòu)從始至終都是一個(gè)熱門課題。總的來說,小波去噪的方法大概可以分為模極大值去噪方法、相關(guān)去噪方法、小波閾值去噪法[2],對(duì)比以上三種方法各自有各自的特點(diǎn),我們?cè)趹?yīng)用中要結(jié)合信號(hào)特征選擇合適的方法。
1.2.1 小波閾值法
小波閾值法降噪是由美國(guó)斯坦福大學(xué)教授Donoho在1994年提出的一種基于閾值估計(jì)和閾值規(guī)則選取的信號(hào)降噪的方法,在小波降噪應(yīng)用領(lǐng)域取得的成績(jī)可佳。對(duì)語音信號(hào)這種具有非平穩(wěn)性和復(fù)雜性的信號(hào),加入白噪聲后得到含噪語音信號(hào),其含噪信號(hào)表示形式[8]如下:
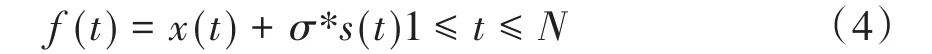
式中,x(t)表示原始信號(hào),s(t)表示白噪聲,σ表示噪聲強(qiáng)度,在最簡(jiǎn)單的情況下可以假設(shè)s(t)為高斯白噪聲,且σ=1。N為離散采樣系列x(t)的長(zhǎng)度。
小波閾值法降噪的具體步驟如圖1:

圖1 小波閾值降噪流程圖
1.2.2 小波硬軟閾值折衷法
小波硬軟閾值折衷去噪方法的原理很簡(jiǎn)單,通俗易懂,就是在閾值估計(jì)器中加入了a因子,當(dāng)a取0時(shí),即為硬閾值小波系數(shù)估計(jì)器,當(dāng)a取1時(shí),即軟閾值小波系數(shù)估計(jì)器。而對(duì)于一般的0<a<1來說,估計(jì)出來的數(shù)據(jù)ω∧j,k的大小介于硬、軟閾值方法之間,因此可以通過在0到1區(qū)間內(nèi)適當(dāng)調(diào)整a因子的大小,來獲得更好的降噪效果。硬、軟閾值折衷法小波系數(shù)估計(jì)器表達(dá)式[9]如下:
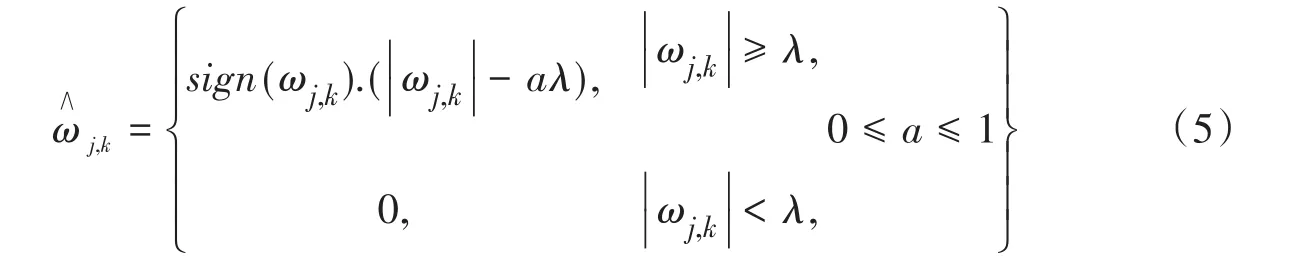
但是該閾值函數(shù)所得到的估計(jì)信號(hào)可能會(huì)產(chǎn)生附加振蕩。于是郭曉霞等人提出了一種改良的硬軟閾值折衷法,該方法優(yōu)于傳統(tǒng)的軟閾值法、硬閾值法、標(biāo)準(zhǔn)的硬軟閾值折衷法[10]。該方法的閾值函數(shù)如下:
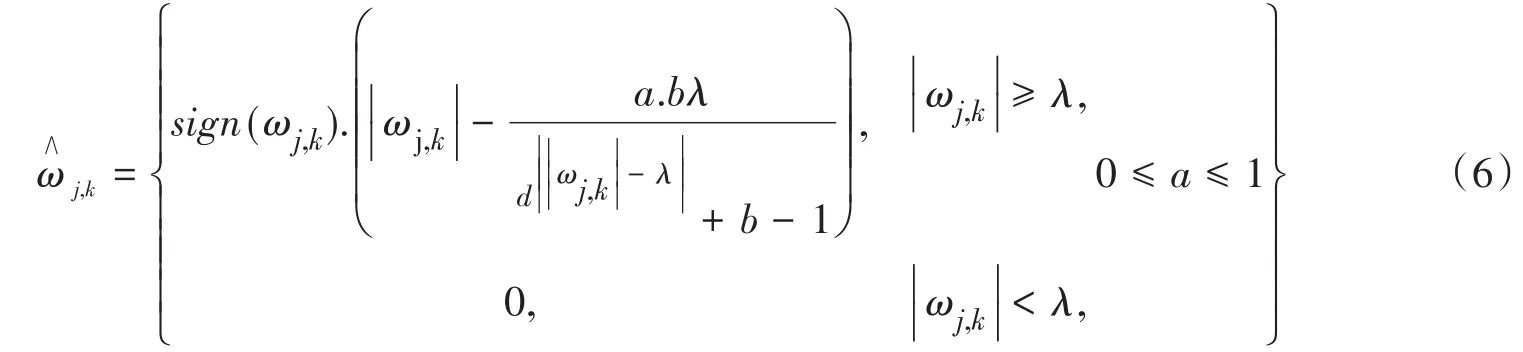
式中b、d均為大于1的實(shí)常數(shù),a、b取任意值時(shí)具有連續(xù)性,根據(jù)實(shí)際情況可調(diào)整b、d的取值。
1.3 EEMD分解基本理論
集合經(jīng)驗(yàn)?zāi)B(tài)分解 EEMD(Ensemble Empirical Mode Decomposition)[11?12]是 Huang針對(duì) EMD方法的不足提出的一種噪聲輔助數(shù)據(jù)分析方法。該方法有效的解決了模態(tài)混疊現(xiàn)象和端點(diǎn)效應(yīng),使真實(shí)的信號(hào)得到了保留,降噪效果也十分明顯。EEMD分解的算法十分通俗易懂,簡(jiǎn)單的來說就是以EMD分解為基礎(chǔ),把白噪聲引入到要分析的信號(hào)中,經(jīng)過多次EEMD分解后,噪音就會(huì)被相互抵消。具體的EEMD分解流程如下[13]:
1)在信號(hào)f(t)中,依次加入n次平均值是零且幅值標(biāo)準(zhǔn)差不變的高斯白噪聲,得到新的信號(hào)fk(t):
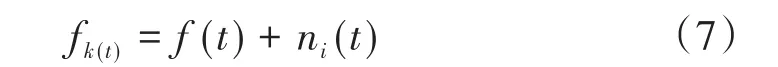
2)對(duì)N組fk(t)依次EMD分解,得到多組IMFS。將第i次添加高斯白噪聲后計(jì)算得到的第j個(gè)IMFS記為fi,j(t)。
3)由于不相關(guān)隨機(jī)序列統(tǒng)計(jì)值為零,對(duì)分解所得IMFS進(jìn)行總體集成平均計(jì)算后,得到最終的IFMS分量。每一個(gè)IFM分量是多個(gè)IMF分量的進(jìn)程平均值。在平均過程中,先前添加的高斯白噪聲對(duì)IMFS產(chǎn)生的影響也得到了抑制,最終獲得EEMD算法處理過的有效IMFS,即:
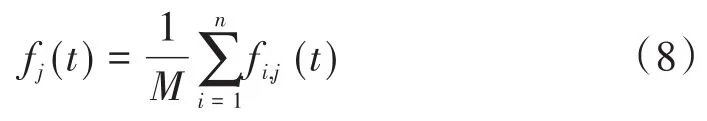
EEMD算法流程圖如圖2所示:
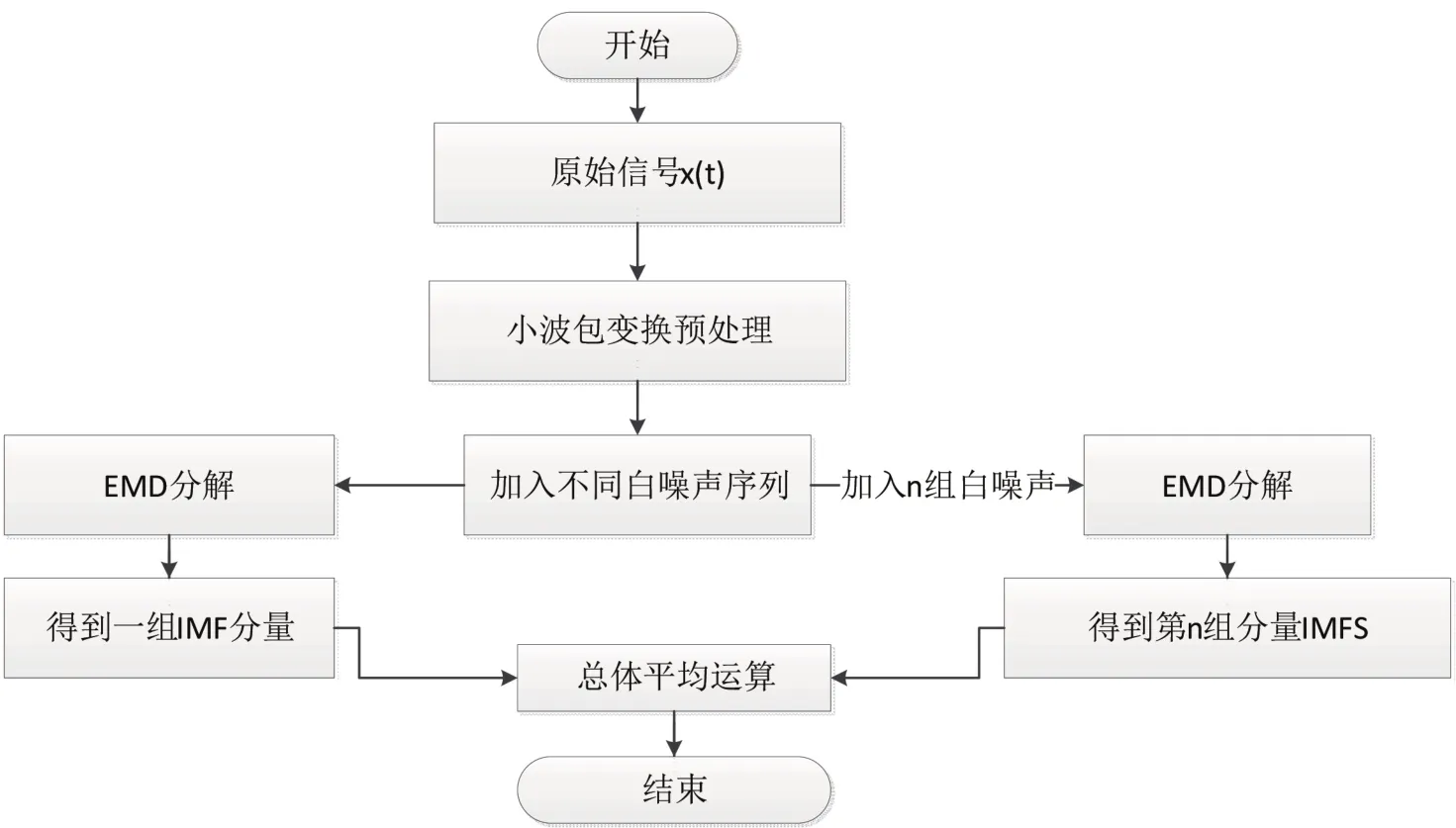
圖2 EEMD分解流程圖
1.4 降噪效果評(píng)價(jià)
所謂信噪比就是信號(hào)和噪聲能量比值的對(duì)數(shù),其定義式[8]為:
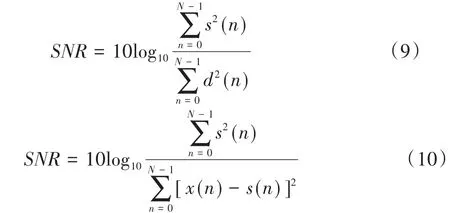
所謂的均方誤差就是原始信號(hào)與去噪后的估計(jì)信號(hào)量之間方差的平方根,其定義式為:
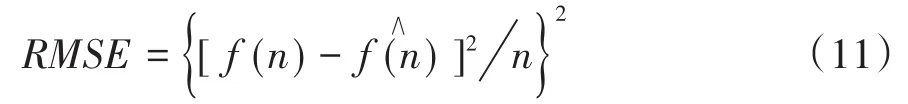
式中f(n)表示原始信號(hào),表示去噪后的信號(hào)。均方誤差越小降噪效果越好。
2 實(shí)驗(yàn)總體方案設(shè)計(jì)
為了使降噪效果更加的可靠,對(duì)模擬的信號(hào)疊加不同信噪比的噪聲。用小波閾值法降噪和EEMD分解結(jié)合小波閾值法對(duì)模擬信號(hào)進(jìn)行降噪,在MATLAB仿真平臺(tái)對(duì)該模擬信號(hào)進(jìn)行降噪處理,驗(yàn)證算法的降噪效果。再把相應(yīng)的算法應(yīng)用到語音信號(hào)的降噪中去。語音信號(hào)降噪流程圖如下:
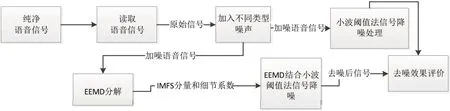
圖3 語音信號(hào)降噪流程圖
基本算法步驟如下:
1)用模擬信號(hào)檢測(cè)小波閾值降噪法和EEMD結(jié)合小波閾值法降噪的可行性;
2)采用小波閾值法降噪方法對(duì)信號(hào)進(jìn)行降噪處理,主要包括三步:選擇適當(dāng)?shù)男〔ɑ头纸鈱訑?shù);選擇適當(dāng)?shù)拈撝岛烷撝岛瘮?shù);進(jìn)行小波分解與重構(gòu);
3)EEMD分解結(jié)合小波閾值法降噪,對(duì)含噪信號(hào)進(jìn)行EEMD分解后,用小波閾值法降噪;
4)通過比較選擇EEMD分解聯(lián)合小波硬軟閾值折衷降噪法對(duì)含噪語音信號(hào)降噪;
5)結(jié)果判別。觀察降和試聽降噪后的語音信號(hào),看是否滿足光滑性和相似性這兩個(gè)信號(hào)降噪原則;
6)對(duì)降噪后的結(jié)果進(jìn)行分析,用信噪比(SNR)和均方誤差(RMSE)來衡量算法的有效性。
3 算法仿真實(shí)驗(yàn)
3.1 模擬信號(hào)降噪
小波閾值法模擬信號(hào)降噪仿真實(shí)驗(yàn):
對(duì)原始模擬信號(hào)y=5*sin(pi*20*t)+3*cos(2*pi*50*t),設(shè)置采樣頻率fs為1 000 HZ,采樣數(shù)據(jù)點(diǎn)N為2 000,n、t、y均為1×2000 double。對(duì)該模擬信號(hào)添加不同信噪比的噪聲,分別用小波軟閾值法、硬閾值法、硬軟閾值折衷法對(duì)含噪語音信號(hào)Y進(jìn)行降噪處理,其中用硬軟閾值折衷法降噪時(shí),在閾值估計(jì)器中加入a因子,在本實(shí)驗(yàn)中取a=0.5。經(jīng)過EEMD分解為9個(gè)IMF分量和1個(gè)剩余分量。然后,計(jì)算出每一個(gè)IMF分量的能量熵,并繪制能量熵值圖。
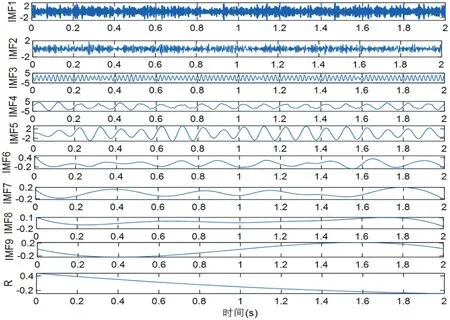
圖4 含噪模擬信號(hào)EEMD分解
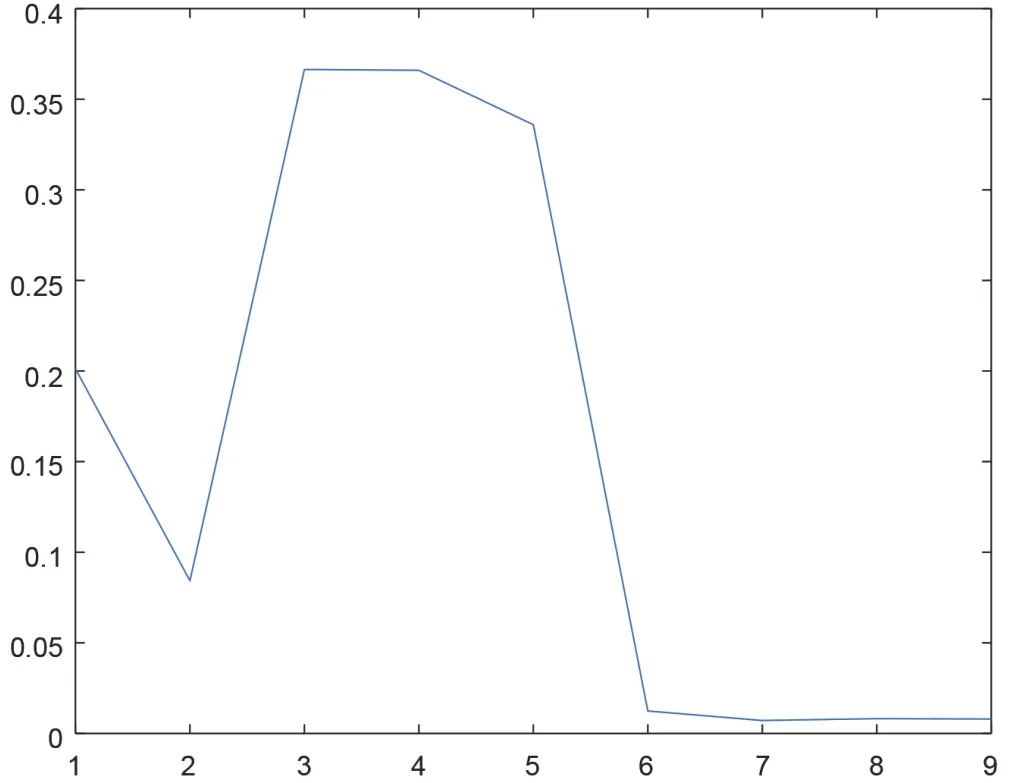
圖5 IMFS分量的能量熵值
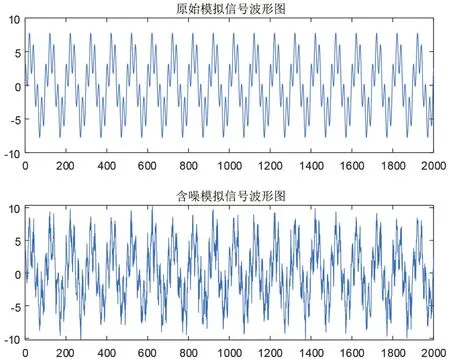
圖6 原始語音信號(hào)與含噪語音信號(hào)波形圖對(duì)比
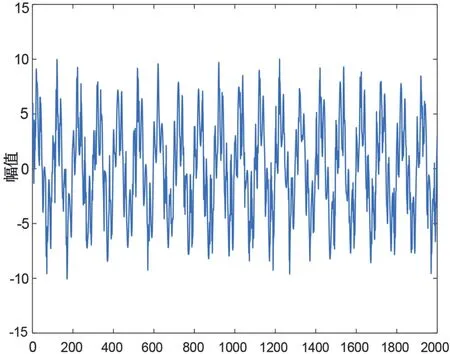
圖7 小波硬軟閾值折衷去噪處理后波形圖
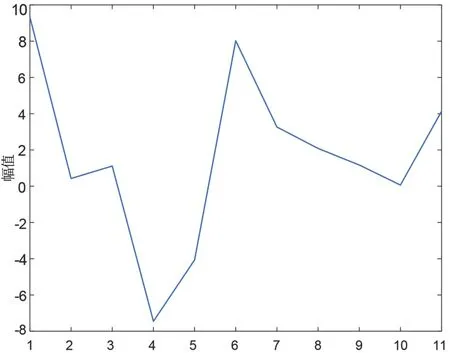
圖8 EEMD結(jié)合小波硬軟閾值折衷去噪處理后波形圖
3.2 語音信號(hào)降噪
小波閾值法語音降噪仿真實(shí)驗(yàn):將下載的源語音信號(hào)“sp01.wav”放在MATLAB 2019a的bin文件目錄下,對(duì)該語音信號(hào)添加不同信噪比的噪聲,采用與用模擬信號(hào)相同的算法對(duì)語音信號(hào)進(jìn)行降噪。在進(jìn)行EEMD分解語音信號(hào)時(shí),向源語音信號(hào)中加入100次信噪比為10 db的隨機(jī)高斯白噪聲,噪聲信號(hào)Y經(jīng)過EEMD分解為13個(gè)IMFS分量和1個(gè)剩余分量,計(jì)算出每一個(gè)IMF分量的能量熵,并繪制能量熵值圖。仿真結(jié)果如下:
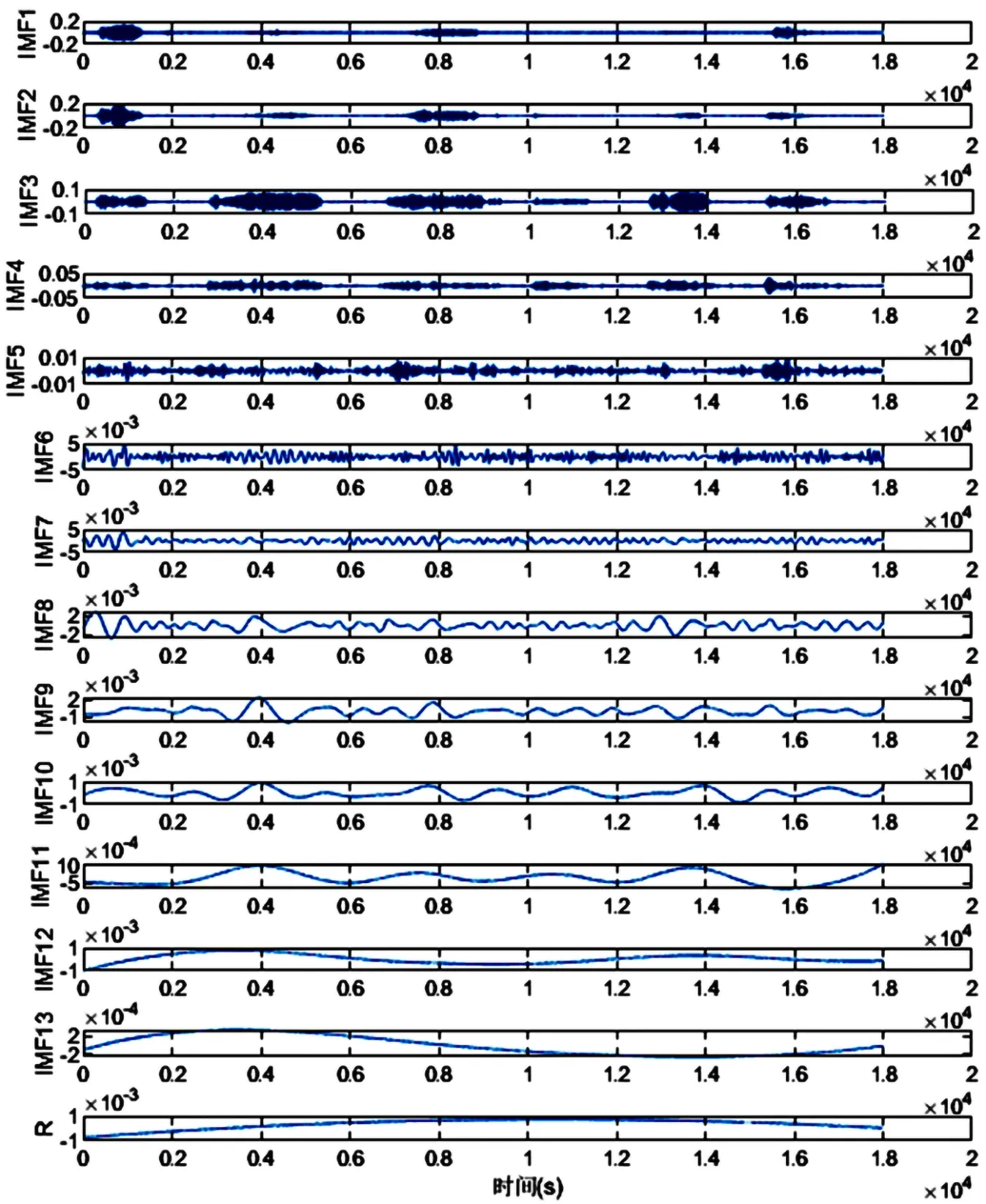
圖9 含噪模擬信號(hào)EEMD分解

圖10 IMFS分量的能量熵值

圖11 源語音信號(hào)和含噪語音信號(hào)波形圖
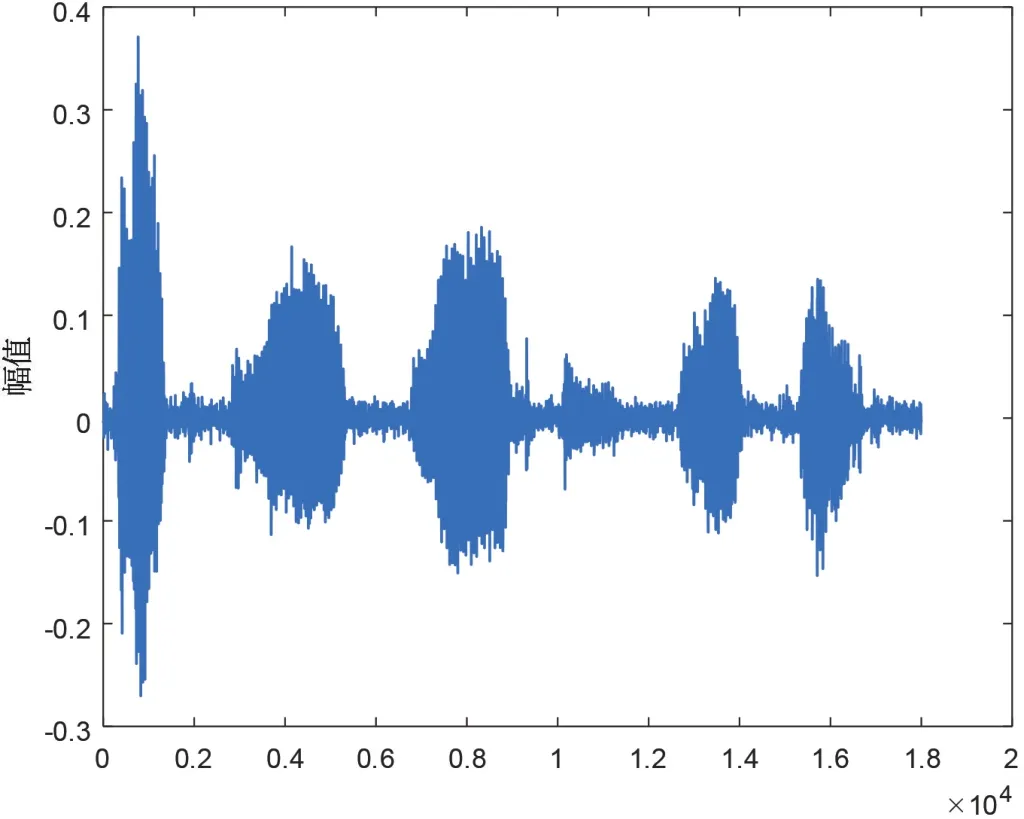
圖12 小波硬軟閾折衷值處理后語音信號(hào)波形圖
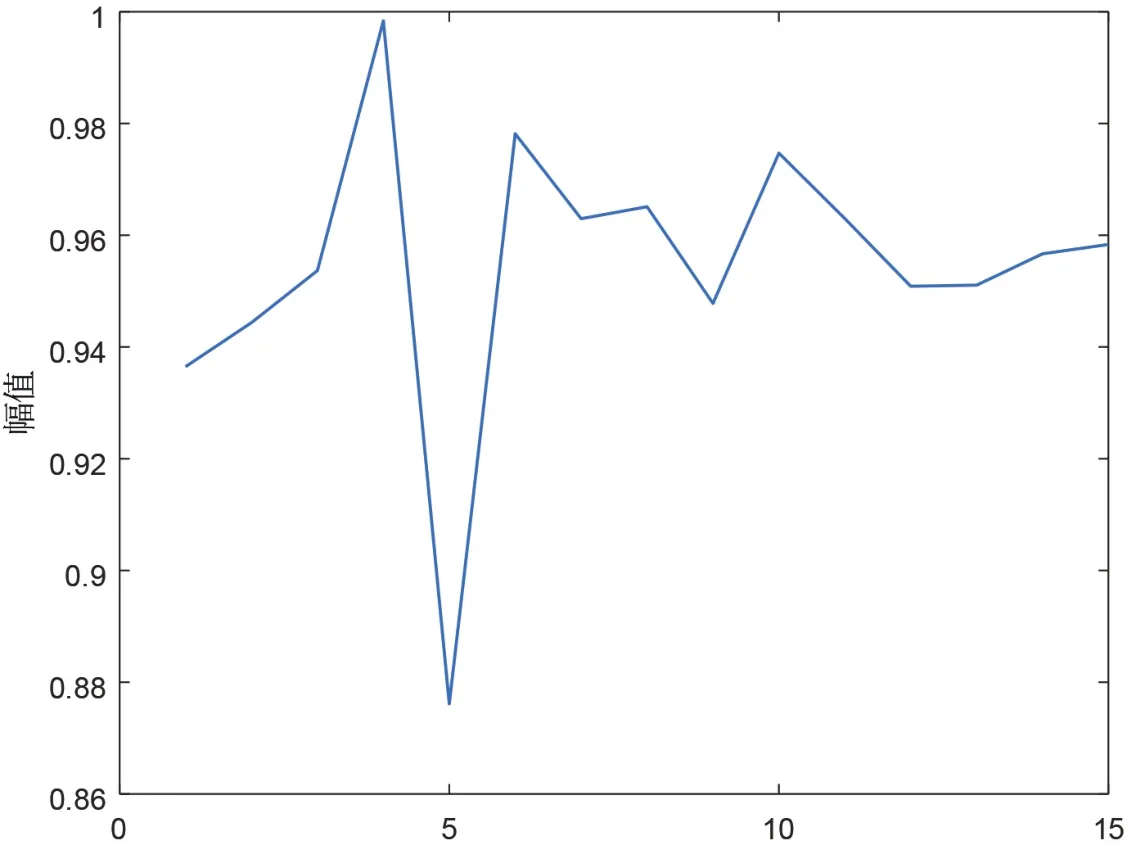
圖13 EEMD-小波硬軟閾折衷值處理后語音信號(hào)波形圖
3.3 實(shí)驗(yàn)結(jié)果分析
對(duì)含噪信號(hào)分別用小波閾值法和EEMD分解結(jié)合小波閾值法進(jìn)行降噪。模擬信號(hào)降噪效果如表1、表2所示,語音信號(hào)降噪效果如表3、表4所示。從表1、表2數(shù)據(jù)可以看出,EEMD結(jié)合小波閾值法降噪后信噪比和均方誤差改善情況較好。其中,在這兩種方法下,在硬閾值、軟閾值、硬軟閾值折衷三種閾值函數(shù)中,硬軟閾值折衷法降噪效果是最好的。因此驗(yàn)證了這兩種算法對(duì)信號(hào)降噪的可行性。

表1 疊加信噪比SNR=10時(shí)不同方法下的降噪信噪比對(duì)比

表2 疊加信噪比SNR=10時(shí)不同方法下的降噪均方誤差對(duì)比

表3 疊加SNR=10時(shí)不同方法降噪后語音信號(hào)信噪比

表4 疊加SNR=10時(shí)不同方法降噪后語音信號(hào)均方誤差
把相應(yīng)的算法應(yīng)用到模擬信號(hào)的降噪中,從表3、表4中可以看出,單純的小波閾值法在硬軟閾值折衷函數(shù)下信噪比只提高了2 db,均方誤差降低了近0.002,EEMD結(jié)合小波閾值法,信噪比提高了近13 db,均方誤差降低了近0.003。可知小波閾值法和EEMD分解結(jié)合小波硬軟閾值法同樣適合對(duì)語音信號(hào)降噪,其中EEMD分解結(jié)合小波閾值法降噪結(jié)果較明顯,而且這兩種方法中,硬軟閾值折衷函數(shù)在語音信號(hào)的降噪中效果最好,且信號(hào)不失真,具有很好的應(yīng)用前景。
4 結(jié)論
將EEMD分解和小波閾值法中的硬閾值、軟閾值、硬軟閾值折衷法相結(jié)合,并應(yīng)用到語音信號(hào)的降噪過程中,對(duì)比試驗(yàn)結(jié)果發(fā)現(xiàn),硬軟閾值折衷法的降噪效果明顯優(yōu)于單純的硬、軟閾值方法,且EEMD結(jié)合小波硬軟閾值法彌補(bǔ)了小波分解中需要預(yù)先設(shè)定小波基和分解層數(shù)的問題,信號(hào)不易失真,降噪效果較好。

