數形結合 解答數學難題

張仁壽

摘 要： 在數學課程體系中，各個知識點之間相互關聯，尤其是在初中階段，教學內容同小學相比，無論是難度、還是深度均有所提升，相應的試題難度也在一定程度上提升，學生極易遇到難題，教師可指導他們運用數形結合思想來解答這些難題，使其突破解題障礙.

關鍵詞： 數形結合;初中數學;解答難題

中圖分類號： G632?????? 文獻標識碼： A?????? 文章編號： 1008-0333（2021）35-0044-02

數學知識本身就具有典型的抽象性特征，學生學習數學過程中離不開邏輯思維的輔助，在初中數學教學中，面對如此眾多的難題，他們容易陷入到困境之中，影響自信心的樹立.面對這一現狀，初中數學教師可以教導學生運用數形結合思想處理難題，將幾何與代數的特點綜合在一起，有效降低解題的難度，將解題過程變得通俗易懂，讓他們順利解答難題.以下筆者就如何運用數學結合解答初中數學難題進行探究，并提出幾點有效的對策.

一、運用以形助數思想，順利解答代數難題

在初中數學教學中，很多數量關系都比較抽象，學生難以準確的把握，這時采用以形助數思想是一個不錯的選擇，就是借助形的幾何直觀性來闡明數之間某種關系，由此將部分思維具體呈現出來，在解題中起著重要作用.初中數學教師可指引學生運用以形助數思想，把數量關系問題轉變成圖形問題，實現由抽象向直觀的轉變，讓他們順利解答代數難題.

例1? 已知0解析? 這是一道典型的不等式問題，將講授到不等式知識時，教師可以設置這一難題，本題目的主要難點在于題設中給出的已知信息較少，只是簡單的確定a和b的范圍，還是以不等式的形式來呈現，而所求證的式子相當長，還涉及到根式、平方式、不等式等相關知識，不僅比較復雜，難度也較大，學生讀完題目以后，很難找準突破口，他們將會陷入到困難直送，不知道該如何解題.此時，教師可以引領學生運用數形結合思想中的以數助形思想，將題目中抽象的數量關系以直觀的幾何圖形展示出來，使其形成清晰的解題思路，從而讓他們快速求證.具體證明過程如下：

證明：如圖1所示，作邊長是1的正方形ABCD，在邊AB上取點E，設AE=a;在邊AD上取點G，使AG=b，過點E和G分別作EF//AD同邊CD相交于點F;作G//AB同邊BC相交于點，設EF和G相交于點O，把AO、BO、CO、DO、AC、BD分別連接起來.學生根 據題目中的條件與要求畫出下面的圖形以后，能夠判斷出三角形AOG、三角形BOE、三角形COF和三角形DOG都直角是直角三角形，所以根據勾股定理能夠得出OA= a2+b2 ， OB= （1-a）2+b2 ，OC= （1-a）2+（1-b）2 ，OD= a2+（1-b）2 ，且AC=BD= 2 ，因為OA+OC≥AC，OB+OD≥BD，所以能夠得出 a2+b2 + （1-a）2+b2 + a2+（1-b）2 + （1-a）2+（1-b）2 ≥2 2 ，但是當且僅當a=b= 1 2 時等號才成立，即為此時該式子的值是2 2 .

對于這道初中數學難題，對于廣大初中生來說一般都無法輕松求證，主要原因在于雖然從表面上看是一個不等式，但是實質上涉及到知識點眾多，處理起來還比較復雜，不過教師可以指引學生在求證這類條件不等式題目時，可根據題設條件作出對應的圖形，然后讓他們運用圖形的幾何性質或者平面幾何的定理、公理去建立不等式，最終使結論獲得證明.

二、采用以數助形思想，有效解答幾何難題

就數學知識來說，形具有顯著的優勢，能形象、直觀的呈現信息，無論什么事物，均具有正反兩面性，形不足之處就是很難做到十分精準，有些圖形較簡單，通過直接觀察難以得出規律，這就要基于代數視角來分析和計算.初中數學教師可根據實際題目引導學生采用以數助形思想，使其借助于數的精確性來闡明形的某些屬性，讓他們有效解答幾何難題.

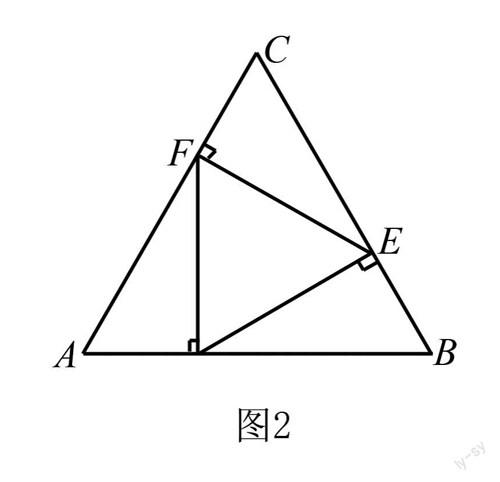
例2? 如圖2所示，在正三角形ABC中，AB、BC、CA三條邊上分別有點D、E、F，如果DE垂直于BC，EF垂直于AC，FD垂直于AB同時成立，求點D在邊AB上的位置.

具體解題方法如下：先假設題干中符合條件的點D、E、F均已經作出，再結合給出的已知條件，尋求三角形中線段和角之間的數量關系，然后采用代數中的方程知識列出含有未知數的等式，以此求解.

解：設邊AB的長度是1，AD的長度是x，由于△ABC是一個正三角形，且DE⊥BC，EF⊥AC，FD⊥AB，所以得到BD=2BE=8x-2，即得出方程x+（8x-2）=1，解之得x= 1 3 ，又因為AD+BD=1，AF=2x，CE=1-2x，CD=2CF=2-4x，BE=1-CE=4x-1，由此說明點D的位置是位于邊AB上的 1 3 分點處.

其實在初中數學幾何教學中，通常存在著這樣一類問題，即為幾何圖形中的某些點的位置或者線段的長度或者角度的大小無法根據題意直觀明了的畫出來，只有根據已知條件求出某一些量時，圖形才能夠畫出，而求那些量的方法，教師可指導學生通過列方程或者方程組進行求解，就是將幾何問題轉化成代數方程計算，讓他們借助數學結合思想解答這類難題.

三、注重數形相互轉化，高效解答數學難題

數與形是數學中最基本和最古老的兩個研究對象，它們在一定條件下能相互轉化.不少初中數學題目并非純粹的以數變形或以形變數，而是需將兩者相互轉換，這就要求學生不能只思考從直觀的形轉換成嚴密的數，也不能只從嚴密的數描述直觀的形，而是以題目中固有的條件與結論為著手點，科學分析與發現數與形的相互轉化關系，高效解答數學難題.

例3? 在數學拓展活動中，某興趣小組為求出 1 2 + 1 4 + 1 8 +……+ 1 2n 的值，先設計出邊長是1的正方形紙，而且通過各種標記把正方形面積的 1 2 ， 1 4 ， 1 8 ……清楚地標注出來，要求你結合已經掌握的數形結合思想推理出假如n是正整數，求出 1 2 + 1 4 + 1 8 +……+ 1 2n 的最終結果，其中可以用n來表示.

具體來說，解題流程如下：學生可以從這個角度展開理解，準備一個邊長是1是正方形，使用剪刀把該正方形紙片剪下來，第一次剪掉這張紙片的一半，那么剩余正方形的面積就是 1 2 ，第二次再將剩下正方形紙片的一半剪下來，得到的圖像面積就是原正方形紙片面積的 1 4 ，第三次把上次剩下的圖形繼續剪掉一半，得出的圖形即為原正方形紙片面積的 1 8 ，以此類推，也就是每次都把上次裁剪剩余圖形面積的一半剪掉，這樣在進行第n次裁剪以后，獲取到的圖形的面積就是（ 1 2 ）n.之后，學生把所有裁剪下來的圖形的面積相加，能夠求出 1 2 + 1 4 + 1 8 +……+ 1 2n 的最終結果是1- 1 2n ，由此計算出該式子的答案.

如此，教師利用這樣一道典型的數學題目展開解題訓練，學生在解題過程中應用數形結合思想時，不僅要用到“以數解形”，還要用到“以形助數”，將 “數”與“形”信息進行靈活自如的轉換，由此實現對數形結合思想的巧妙應用，同時訓練他們的數學思維品質，將復雜數學難題變得簡單化，使其形成最優解題思路，最終快速、準確的計算出答案.

參考文獻：

[1]謝立影.淺析初中數學教學中數形結合方法的具 體應用策略[J].天天愛科學（教育前沿），2021（09）：69-70.

[2] 劉洪燕.初中數學教學中數形結合思想應用能力培養探討[J].中學課程輔導（教師通訊），2021（16）：100-101.

[3]徐曉霞，王洪英.數形結合思想在初中數學解題中的應用[J].現代中學生（初中版），2021（Z4）：66-67.

[4]李三平.初中數學教學中學生數學解題能力的培養[J].數理化解題研究，2021（17）：24-25.

[責任編輯：李 璟]