基于三階牛頓–埃爾米特插值全離散法的銑削穩(wěn)定性預(yù)測*

黃 超，楊文安，黃久超，解菲菲，楊有成

（1.上海航天精密機械研究所，上海 201600；2.南京航空航天大學(xué)機電學(xué)院，南京 210016）

銑削作為一種高效的切削加工方法，具有加工精度高、材料去除率大和加工成本低等優(yōu)點。在銑削過程中，主要存在的振動形式有自由振動、受迫振動及自激振動，其中自激振動中的再生顫振是引起加工過程不穩(wěn)定的主要因素[1–2]。銑削顫振通常會導(dǎo)致加工零件表面質(zhì)量差、刀具磨損加劇以及數(shù)控機床壽命降低等問題[3]。此外，考慮再生顫振的銑削動力學(xué)模型可以近似地描述為時滯微分方程，通過求解時滯微分方程可以獲得穩(wěn)定性葉瓣圖，達到銑削穩(wěn)定性預(yù)測的目的[4]。因此，如何快速精確地獲取銑削穩(wěn)定性葉瓣圖顯得尤為重要。

迄今為止，預(yù)測銑削穩(wěn)定性的方法主要分為數(shù)值法[5–6]和解析法[7–16]。Davies等[5]提出了一種改進的時域計算方法預(yù)測出了小徑向切深切削下的額外不穩(wěn)定區(qū)域。Li等[6]提出了基于Runge–Kutta法的銑削穩(wěn)定性時域分析方法，但計算效率太低。Altintas等[7]提出了一種經(jīng)典的零階解析方法，但是該方法不能預(yù)測小徑向切深切削下的銑削穩(wěn)定性。Merdol等[8]提出了考慮了周期力系數(shù)矩陣的高階展開項多頻率法，實現(xiàn)了小徑向切深切削下的穩(wěn)定性預(yù)測。Insperger等[9]通過對時滯項進行離散處理，提出了具有高精度的時域數(shù)值穩(wěn)定性預(yù)測方法。Ding等[10–11]基于直接積分思想提出了包括一階全離散法（1stFDM）和二階全離散法的穩(wěn)定性預(yù)測方法。全離散法利用線性插值同時逼近時滯微分方程中的狀態(tài)項和時滯項，極大提高了方法計算效率。Ding等[12]隨后提出了一種基于牛頓–柯特斯公式的數(shù)值積分法，該方法通過直接離散積分方程的積分項構(gòu)造出相鄰周期的轉(zhuǎn)移矩陣來預(yù)測銑削穩(wěn)定性。隨后，Zhang等[13]在此基礎(chǔ)上通過辛普森公式提出了一種全新的銑削穩(wěn)定性預(yù)測方法。最近，Yan等[14]基于全離散法，提出了一種改進的三階全離散法（3rdUFDM），得到了比一階、二階全離散法更高的預(yù)測精度和計算效率。Dai等[15]提出了一種基于黃金比例搜索的改進全離散方法來預(yù)測銑削穩(wěn)定性，并且引入精細積分法來計算矩陣指數(shù)，極大地提高了該方法的計算效率。Li等[16]利用泰勒公式對非齊次項二次展開，提出了顯式精細積分法預(yù)測銑削穩(wěn)定性。

本文基于再生顫振理論構(gòu)建的銑削動力學(xué)模型，提出一種高精度、高效率的預(yù)測銑削穩(wěn)定性的三階牛頓–埃爾米特插值全離散法。

1 動力學(xué)模型

1.1 單自由度動力學(xué)模型

一般來說，考慮再生顫振的單自由度銑削動力學(xué)模型表述為時滯微分方程[9]：

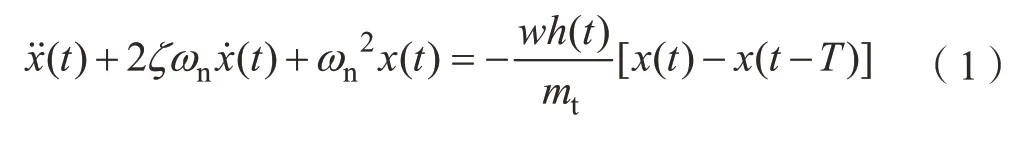
式中，mt，ζ和ωn分別表示刀具的模態(tài)質(zhì)量、刀具的阻尼比和自然頻率；w為軸向切削深度；x(t)為刀具模態(tài)坐標；時滯量T等于刀齒切削周期，即T=60/(NΩ)，N為刀具齒數(shù)，Ω為主軸轉(zhuǎn)速（r/min）；切削力系數(shù)h(t)表示為：

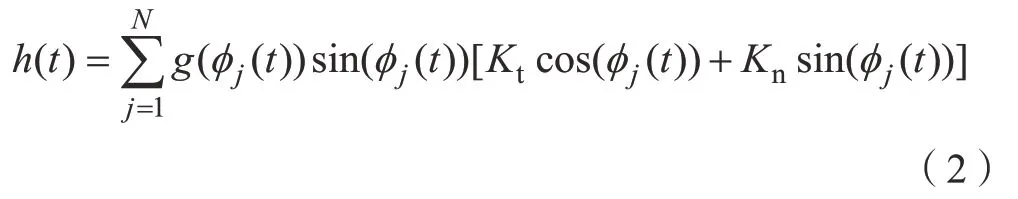
式中，Kt和Kn分別為切向和徑向切削力系數(shù)；?j(t)為第j個刀齒轉(zhuǎn)角：

函數(shù)g(?j(t))定義為：

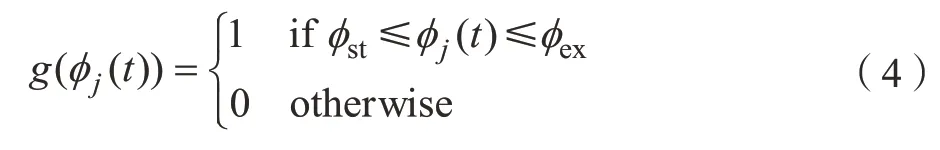
其中，?st和?ex分別是刀齒的切入與切出角。對于順銑，?st=arcos(2a/D–1)，?ex=π；對于逆銑，?st=0，?ex=arcos(1–2a/D)，其中a/D為徑向切深與刀具直徑之比。

令x(t)=[x(t)mx.(t)+mζωnx(t)]T，單自由度銑削模型的狀態(tài)空間形式為：

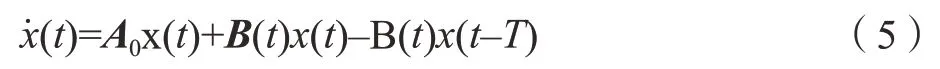
1.2 雙自由度銑削模型

不失一般性，考慮再生顫振的雙自由度銑削動力學(xué)模型表述為時滯微分方程[9]：

式中，mt，ζ和ωn分別為刀具的模態(tài)質(zhì)量、刀具的阻尼比和自然頻率；w為軸向切削深度；并假設(shè)它們在x和y兩個方向是相等的，hxx(t)，hxy(t)，hyx(t)和hyy(t)為如下函數(shù)：

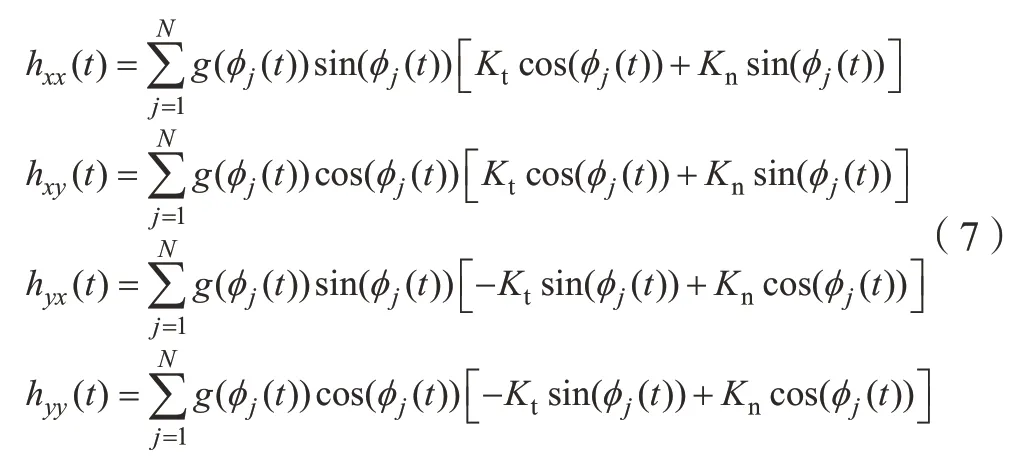
同樣地，雙自由度銑削模型的狀態(tài)空間形式為：

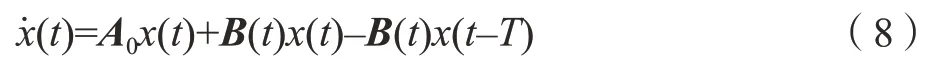
其中，

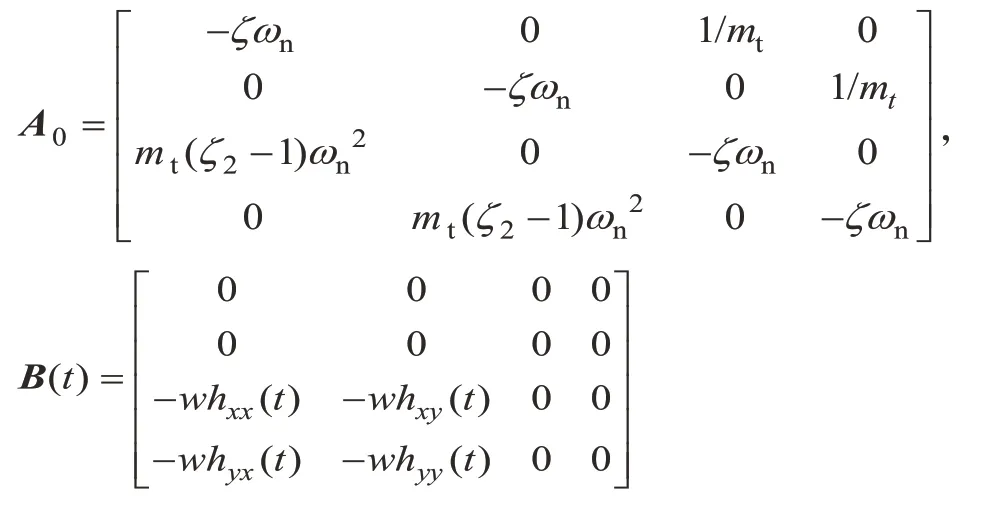
2 三階牛頓–埃爾米特插值全離散法

由前文可知，考慮再生顫振的銑削動力學(xué)方程可由以下n維狀態(tài)空間方表述：

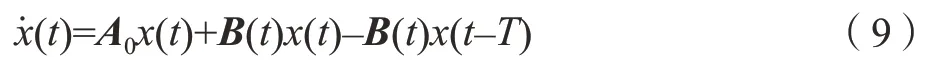
式中，A0是表示系統(tǒng)時不變性質(zhì)的常數(shù)矩陣，B(t)為周期系數(shù)矩陣，并滿足B(t+T)=B(t)。

三階牛頓–埃爾米特插值全離散法的第1步是將刀齒切削周期T離散為m個相等的時間區(qū)段，即T=mτ（其中m為正整數(shù)）。在每一個時間區(qū)段kτ≤t≤(k+1)τ，（k=0，…，m）上，以xk=x(kτ)為初始條件，式（9）的響應(yīng)可以表示為：

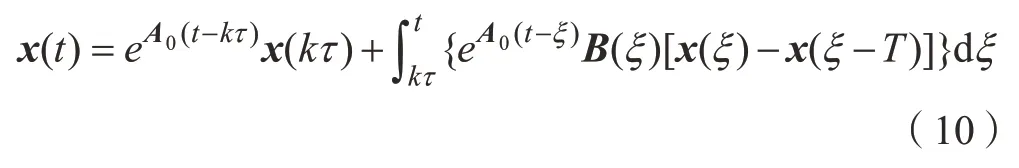
令f(ξ)=B(ξ)x(ξ)，v(ξ)=B(ξ)x(ξ–T)，式（10）可以等效表示為

其中，δ=ξ–kτ，δ∈[0，τ]。求解式（11）中的積分項時首先構(gòu)造牛頓插值多項式：

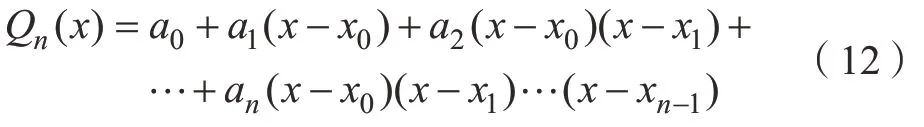
其中，系數(shù)ai（i=0，1，…，n）由插值條件得

由插值條件Qn(x0)=f(x0)得：

由插值條件Qn(x1)=f(x1)得：

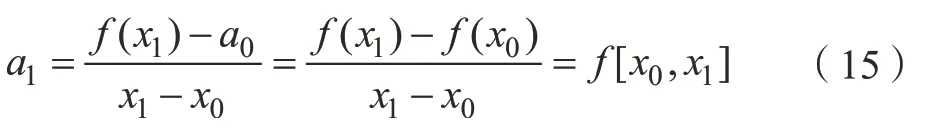
一般可得：

這樣得到滿足插值條件Qn(x1)=f(x1)，(i=0，1，…，n)的n次牛頓插值多項式

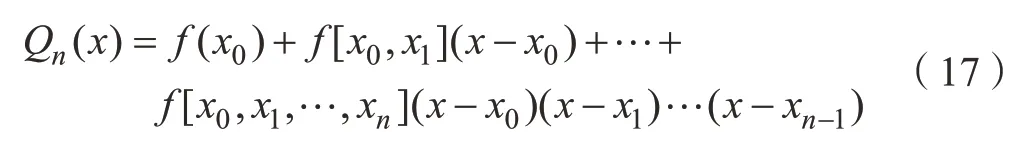
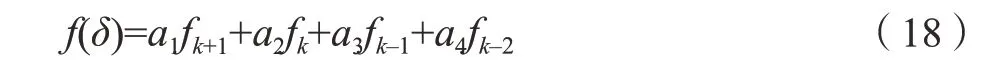
其中，

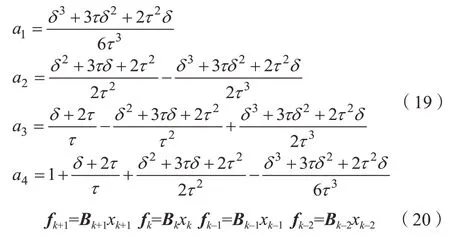
其中，Bk表示B(t)在時間點tk=kτ的取值。然后構(gòu)造埃爾米特插值多項式，給定f(x)在n+1個節(jié)點a=x0＜x1＜…＜xn=b上的函數(shù)值f(x0)，f(x1)，…，f(xn)，以及一階導(dǎo)數(shù)值f'(x0)，f'(x1)，…，f'(xn)。則可在每個小區(qū)間[xi，xi+1]上構(gòu)造3次埃爾米特插值多項式

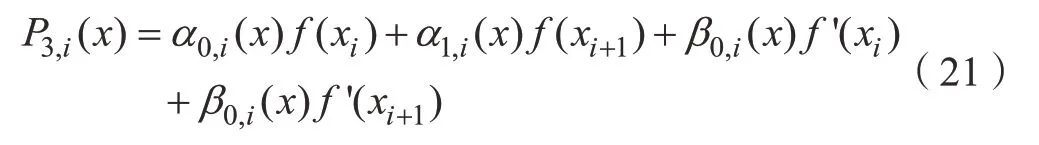
其中，

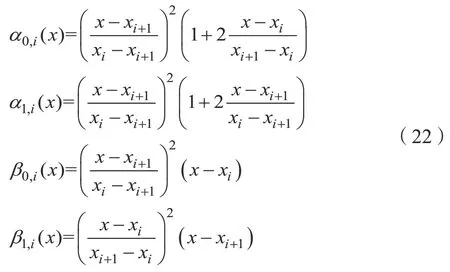
所以，在時間區(qū)間[(k–m)τ，(k+1–m)τ]中，時滯項v(δ–T)可通過埃爾米特插值獲得：

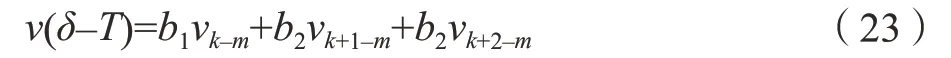
其中，

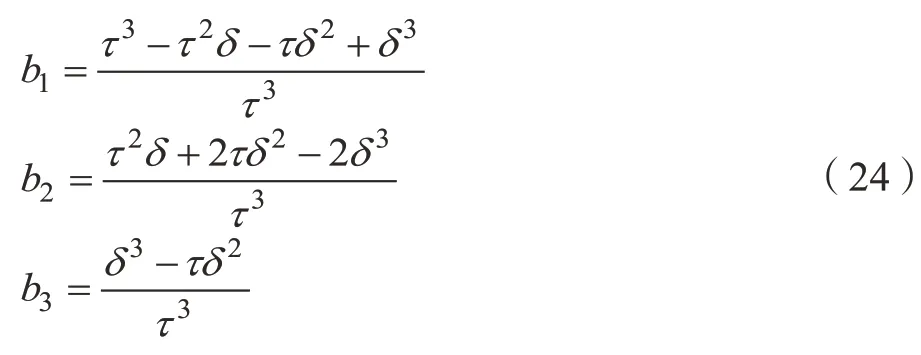
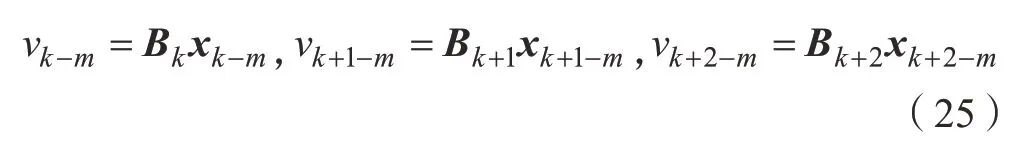
將式（18）～（25）代入式（11），簡化的銑削系統(tǒng)表達式為：

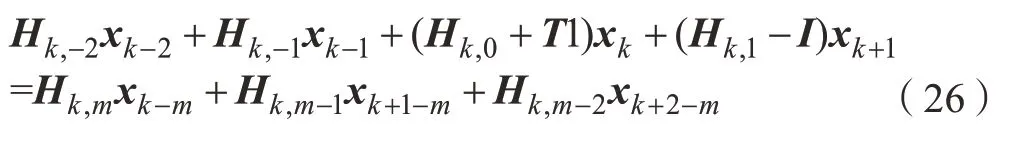
其中，

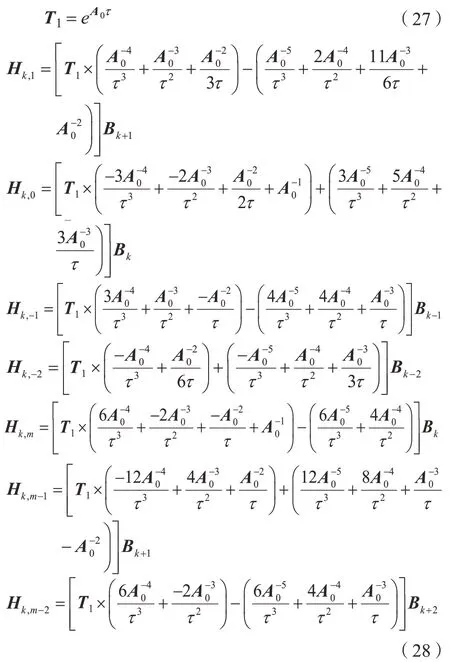
基于矩陣指數(shù)的加法定理，矩陣指數(shù)T1可寫為

其中，dt=Δt/2n。為了提高計算精度，一般取n=20，精細區(qū)段dt就已經(jīng)非常小的區(qū)段了[17]。當(dāng)dt非常小時，可采用Taylor級數(shù)展開近似矩陣指數(shù)，即

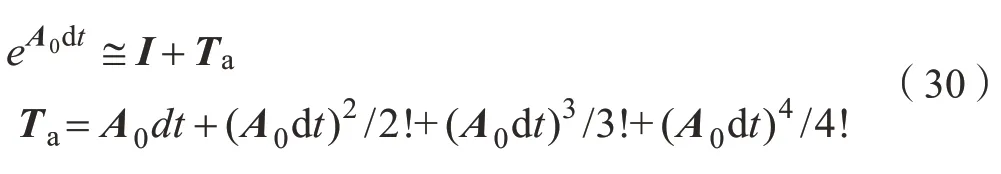
將式（30）代入式（29），矩陣指數(shù)T1近似解為

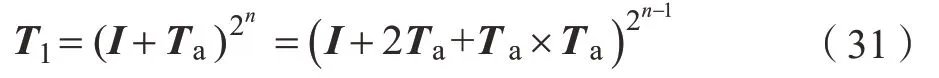
執(zhí)行以下運算，

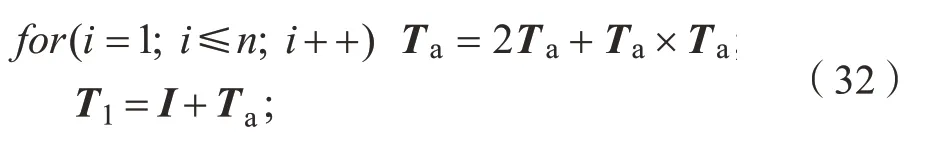
由式（26）可以構(gòu)造如下離散映射

其中，

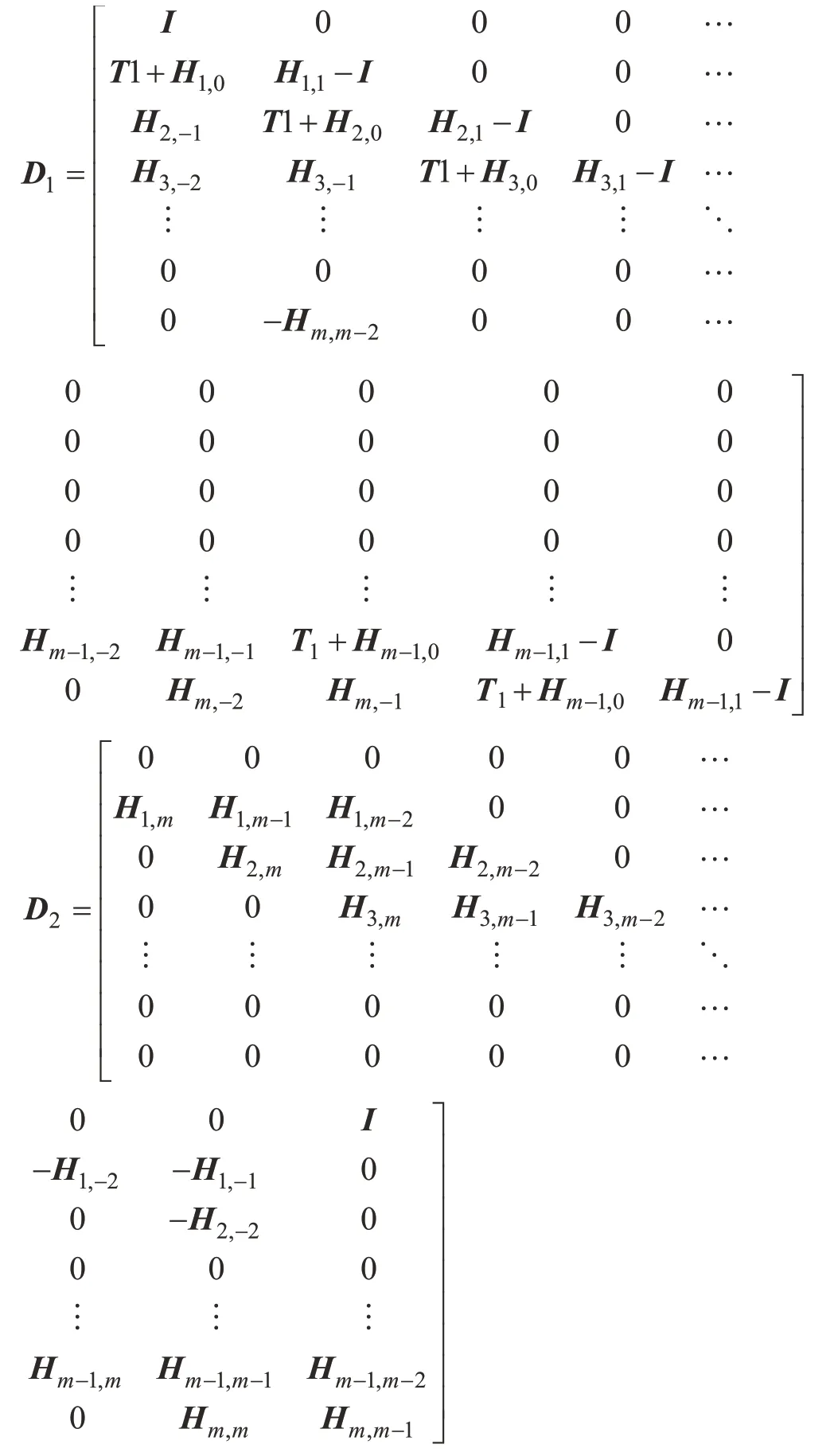
然后，系統(tǒng)在單個時間周期上的狀態(tài)轉(zhuǎn)移矩陣Ф定義為

最后，根據(jù)Floquet理論，若系統(tǒng)轉(zhuǎn)移矩陣Ф特征值都小于1，則系統(tǒng)穩(wěn)定；否則，系統(tǒng)發(fā)生顫振。

3 數(shù)值仿真結(jié)果分析

3.1 收斂性分析

局部離散誤差分析可以反映所提方法近似解收斂速度的快慢。將局部離散誤差||μ|–|μ0||表示為周期離散數(shù)m的函數(shù)，其中參考值|μ0|是m=500時采用1stFDM得到的特征值的模。以單自由度銑削動力學(xué)模型為例，對本文所提出方法與1stFDM和3rdUFDM的收斂性進行分析。本文中數(shù)值仿真所采用的仿真參數(shù)均與文獻[14]相同。切削參數(shù)為：切向力系數(shù)Kt=6×108N/m2，法向力系數(shù)Kn=2×108N/m2，徑向切深比a/D=1，主軸轉(zhuǎn)速Ω=5000r/min，軸向切削深度w=0.2mm、0.5mm、0.7mm、1mm。模態(tài)參數(shù)：順銑，刀具齒數(shù)N=2，模態(tài)質(zhì)量mt=0.03993kg，模態(tài)阻尼ζ=0.011，固有頻率ωn=922×2πrad/s。本文所有仿真均在臺式機電腦（Inter(R) Core(TM) i5-7400 CPU, 8GB）上運行，運行平臺為MATLAB 9.2，操作系統(tǒng)為Windows 10。

圖1給出了1stFDM、3rdFDM和文中方法在4種不同軸向切削深度時的局部離散誤差變化趨勢。由圖1可知，隨著離散數(shù)m的增加，1stFDM、3rdUFDM和文中方法的局部離散誤差逐漸接近于零。在離散數(shù)相同的情況下，文中方法的局部離散誤差最小。比如主軸轉(zhuǎn)速Ω=5000r/min，軸向切削深度w=0.7mm，離散數(shù)m=45時，1stFDM、3rdUFDM和文中方法的局部離散誤差分別為0.043，0.014和0.003，文中方法的計算精度比1stFDM和3rdUFDM的計算精度分別提高約93%和79%。在相同的局部離散誤差下，文中方法所需的周期離散數(shù)更小。因此，文中方法的計算效率遠遠高于1stFDM和3rdUFDM。

文中方法兩自由度的局部離散誤差變化趨勢如圖2所示。兩自由度銑削過程的系統(tǒng)參數(shù)取值的大小與單自由度的參數(shù)相同。由圖2可知，兩自由度模型的收斂速度和單自由度模型的收斂速度一樣快，且當(dāng)離散誤差m=40時都接近于0。

3.2 穩(wěn)定性葉瓣圖

3.2.1 單自由度銑削模型

在單自由度銑削模型中，為了比較穩(wěn)定性邊界的計算精度，分別使用1stFDM、3rdUFDM和文中方法獲得穩(wěn)定性葉瓣圖。將模態(tài)參數(shù)設(shè)置與3.1節(jié)相同，主軸轉(zhuǎn)速5000≤Ω≤10000r/min，軸向切削深度0≤w≤10mm，徑向比a/D=1，順銑，主軸轉(zhuǎn)速與軸向切削深度平面的網(wǎng)格數(shù)為200×100。當(dāng)離散數(shù)m足夠大時，1stFDM獲取的穩(wěn)定性邊界接近于真實值[10]。因此，取離散數(shù)m=200，1stFDM獲取的穩(wěn)定性葉瓣圖作為參考并在圖中以紅色給出。

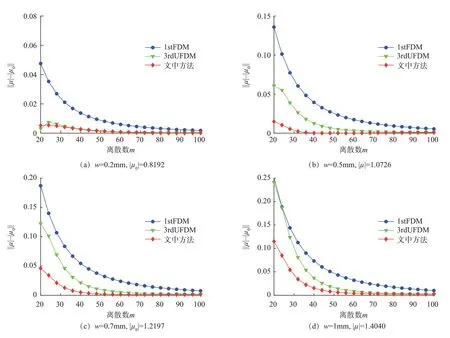
圖1 1stFDM、3rdUFDM和本文方法收斂速度的比較Fig.1 Convergence rate comparison of 1stFDM, 3rdUFDM and proposed method

圖3給出了在不同離散數(shù)下3種方法所得的穩(wěn)定性葉瓣圖與參考曲線的對比結(jié)果，同時給出了計算時間。可知，隨著離散數(shù)m的增加，3種方法的計算精度逐漸提高。顯然當(dāng)離散數(shù)m相同時，文中方法的計算精度比1stFDM和3rdUFDM的計算精度都高，而且計算時間都是最短的。所以，文中方法是一種具有較高的計算精度和計算效率的銑削穩(wěn)定性預(yù)測方法。

3.2.2 雙自由度銑削模型

雙自由度銑削過程的系統(tǒng)參數(shù)取值的大小與單自由度的參數(shù)相同。周期離散數(shù)m取為40，主軸轉(zhuǎn)速與軸向切削深度平面劃分為200×100網(wǎng)格點，徑向切深比a/D=0.05，0.1，0.5順銑。在雙自由度銑削模型中，1stFDM、3rdUFDM和文中方法的銑削穩(wěn)定性葉瓣圖計算結(jié)果和時間列于圖4中。可知，當(dāng)a/D=0.5時，在沒有損失任何計算精度的前提下，文中方法的計算時間較1stFDM縮短21%，較3rdUFDM縮短9%。故文中方法是一種更加高效的銑削穩(wěn)定性預(yù)測方法。

4 試驗驗證

針對本文提出的用于預(yù)測銑削穩(wěn)定性的算法，本節(jié)通過試驗對銑削穩(wěn)定性預(yù)測結(jié)果進行驗證。Gradisek等[18]已經(jīng)通過試驗驗證了半離散法的有效性，所以本次驗證試驗所用的模態(tài)參數(shù)和切削試驗數(shù)據(jù)均與文獻[18]相同，仿真結(jié)果和試驗結(jié)果如圖5所示。

可以看出，當(dāng)徑向比a/D取1、0.5和0.1時，文中方法所獲得的穩(wěn)定性葉瓣圖很好地預(yù)測出了銑削系統(tǒng)的穩(wěn)定區(qū)域。對于小徑向銑削，即a/D=0.05，文中方法所獲得的穩(wěn)定性葉瓣圖和試驗結(jié)果還是吻合的，但是在主軸轉(zhuǎn)速11000≤Ω≤17000r/min時預(yù)測誤差較大，這可能是由于本文使用的銑削動力學(xué)模型沒有考慮實際銑削過程中存在的某些非線性因素，導(dǎo)致上述穩(wěn)定性葉瓣圖與實際試驗之間存在誤差。綜上可見，本文方法是一種高效準確的預(yù)測銑削穩(wěn)定性的方法。

5 結(jié)論

針對考慮再生顫振的銑削動力學(xué)模型，本文提出了三階牛頓–埃爾米特插值全離散法預(yù)測銑削穩(wěn)定性。

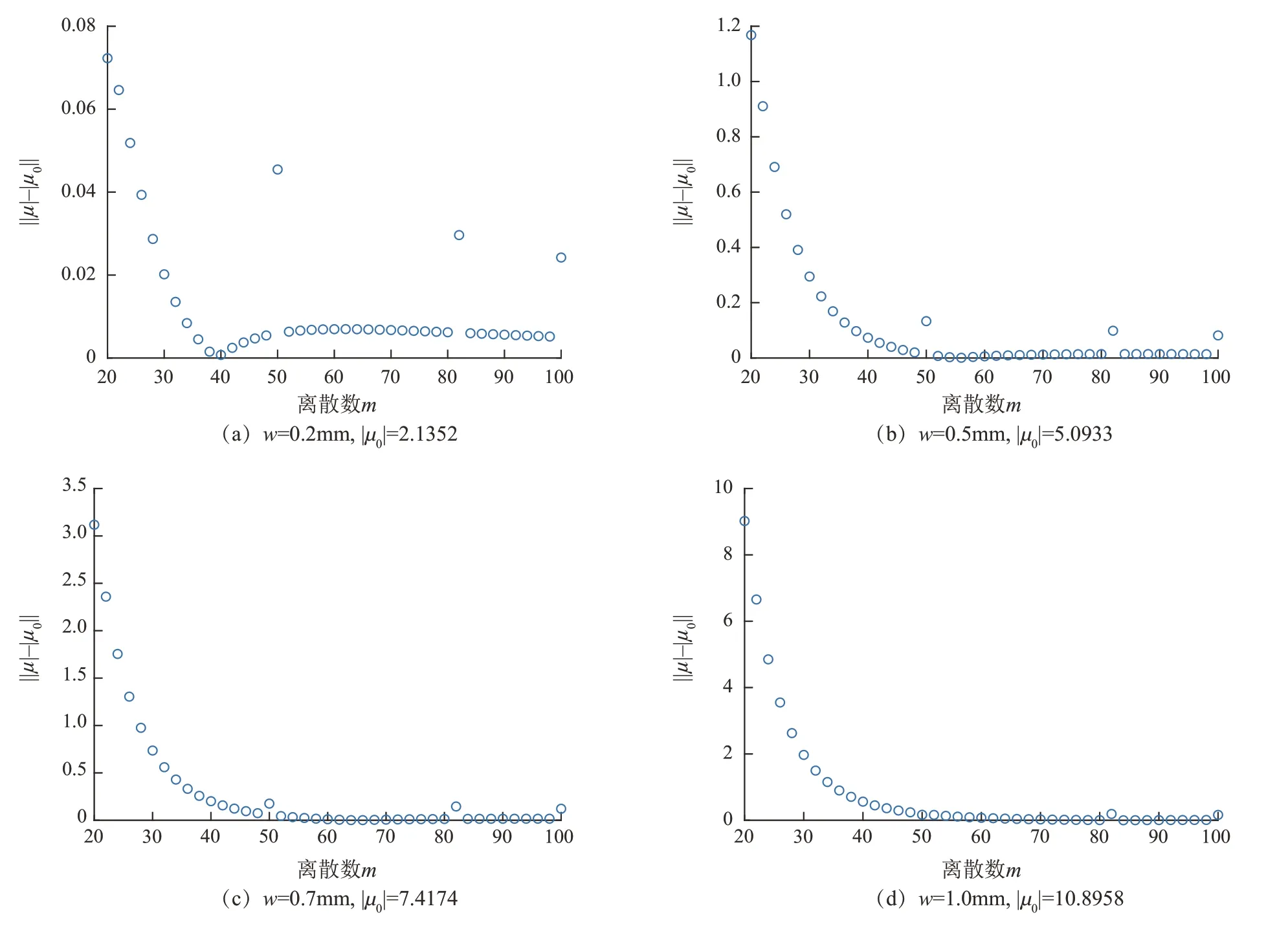
圖2 本文方法兩自由度收斂速度Fig.2 Convergence rate of the proposed method for two degree-of-freedom

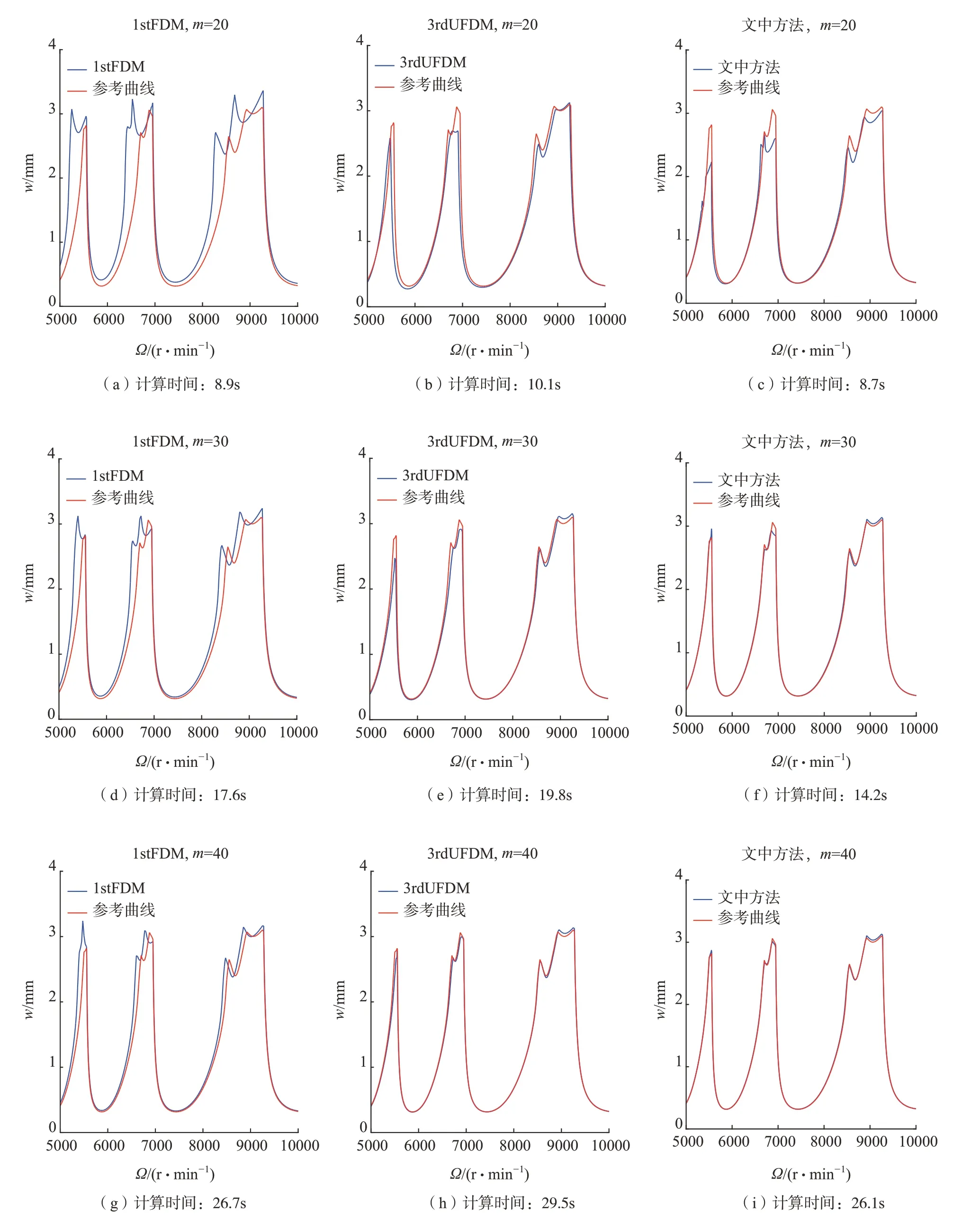
圖3 1stFDM、3rdUFDM和文中方法對于單自由度模型的穩(wěn)定性葉瓣圖Fig.3 Stability lobes of 1stFDM, 3rdUFDM and proposed method in this paper for a single degree of freedom model

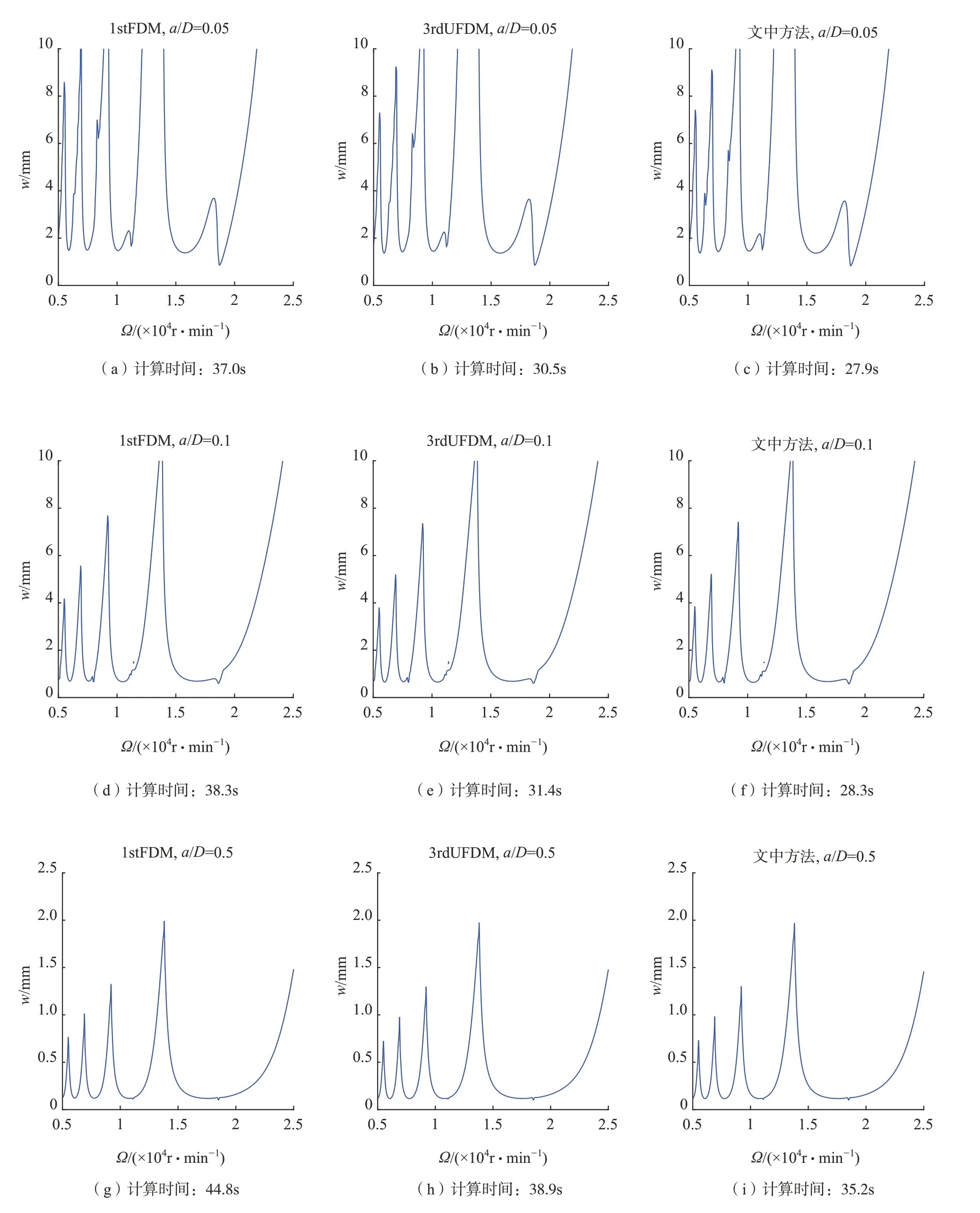
圖4 1stFDM、3rdUFDM和文中方法對于雙自由度模型的穩(wěn)定性葉瓣圖Fig.4 Stability lobes of 1stFDM, 3rdUFDM and proposed method in this paper for two-degree-of-freedom model

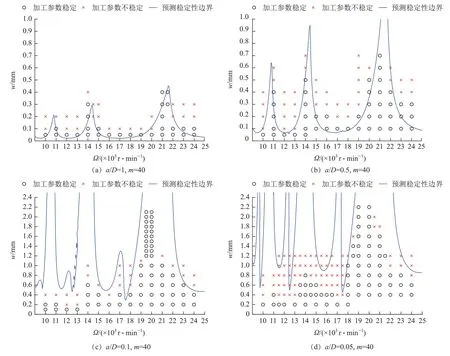
圖5 文中方法的穩(wěn)定性預(yù)測結(jié)果和試驗驗證結(jié)果Fig.5 Predicted stability boundaries and stability obtained from experiment

（1）通過對局部離散誤差的分析可知，文中方法的計算精度比1stFDM和3rdUFDM的計算精度分別提高約93%和79%。隨著軸向切削深度增加，文中方法在較少的離散數(shù)時能達到1stFDM和3rdUFDM較多離散數(shù)時的局部離散誤差。

（2）在單自由度銑削模型中，隨著離散數(shù)的增加，以上3種方法的計算精度都逐漸提高。當(dāng)離散數(shù)相同時，文中方法的計算精度高于1stFDM和3rdUFDM，并且計算效率也是最高的。在雙自由度銑削模型中，當(dāng)離散數(shù)相同時，3種方法的計算精度相當(dāng)，但文中方法的計算效率比1stFDM提高約21%，比3rdUFDM提高約9%。

（3）試驗表明，文中方法可以高效準確地預(yù)測銑削穩(wěn)定性。