具有年齡結構的MSIQRS傳染病模型的穩定性分析*

豆中麗

重慶財經學院，重慶400055

傳染病是由病毒、細菌和寄生蟲等感染人體后具有傳染性的疾病［1］，關于傳染病模型的研究已有很多成果［2-4］。現代醫學說明隔離是預防和控制傳染病的有效手段之一，例如在2003年爆發的SARS傳染病，采用有效的隔離措施切斷了傳染病的傳播途徑，由此可見隔離對于SARS疫情的控制功不可沒，因此建立帶有隔離治療的數學模型來說明這一問題顯得尤為重要［5-6］。但是由于不同年齡的人群對同一疾病的感染程度不一樣，有些疾病（如風疹、小兒麻痹、百日咳等）只在兒童中傳播，有些疾病（如性病）只在成人中傳播，所以研究年齡結構的流行病模型有著重要的理論和實際意義［7-9］。在上述文獻研究的基礎上，本文討論了一類具有隔離的年齡結構MSIQRS傳染病模型，給出了平衡點的存在性及穩定性條件，并用基本再生數的表達式解釋了隔離治療對于預防控制疾病的重要性。

1 模型建立

2 基本再生數的表達式和無病平衡點的局部穩定性

本節中我們將給出基本再生數R0和接種再生數R(φ)的表達式，R0表示染病個體在其整個染病期間易感人口中所感染的新病人平均數。

由于模型（3）的平衡解滿足

3 無病平衡點的全局穩定性

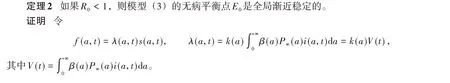
4 地方病平衡點的存在性和穩定性

5 討 論

基本再生數R0表示一個病人在其染病期間所感染的病人數。一旦隔離成功后，則基本再生數R0＜1，這說明隔離后可以使再生數減少，即新感染病人數減少，使無病平衡點穩定，從而有利于病疫的控制消除傳播。當R(φ) ＜1 時，無病平衡點局部漸近穩定；當R0＜1 時，無病平衡點全局漸近穩定性，說明傳染病逐漸的趨于滅絕；當R(φ) ＞1 時，地方病平衡點局部漸近穩定的，這說明傳染病不會消除，而是逐漸趨于穩定，形成一種地方病。