基于接收機鐘差約束的精密單點定位時間傳遞研究

趙傳寶，盛傳貞，張寶成

(1.衛星導航系統與裝備技術國家重點實驗室，石家莊 050081；2.中國科學院精密測量科學與技術創新研究院，武漢 430000；3.中國科學院大學，北京 100000)

0 引言

精密單點定位(PPP)是一種能夠利用單臺接收機的測碼偽距和載波相位觀測值并借助外部高精度軌道鐘差產品進行絕對定位的技術[1].PPP 技術起初主要應用于精密位置確定等應用，后來張寶成[2-3]提出了非組合PPP 模型，該方法開始逐漸廣泛應用于電離層、對流層等空間大氣的研究.2016 年PPP 技術開始逐漸應用到時間傳遞領域[4].國內外相關學者均對PPP 授時與時間傳遞進行了深入地研究[5-6].作為一種全視方法(AV)，由于PPP 可以利用測站處可觀測到的全部衛星數據，因此時間傳遞性能不會受兩測站間距離長短的影響，具有更高的靈活性[7-9].目前，國際計量(BIPM)已將PPP 作為國際原子時(TAI)主要的例行時間傳遞技術之一[10].

隨著氫原子鐘的不斷普及，越來越多的監測站配備了氫原子鐘作為外部高精度時間頻率基準.氫原子鐘相對于銣、銫等原子鐘具有更高的穩定性[11-12].但是在傳統的PPP 時間傳遞數據處理中通常將接收機鐘差參數視為白噪聲(WN)進行處理，這在一定程度上浪費了氫原子鐘的高穩定性信息.為了充分利用氫原子鐘高度穩定的特性，本文通過20 個全球分布的國際GNSS 服務(IGS)測站，90天的GPS 觀測數據基于Hadamard 方差得到了經驗的氫原子鐘方差特性，并在PPP 解算中將相鄰兩歷元的接收機鐘差參數約束為隨機游走模型進行處理，從而提高PPP 時間傳遞性能.為了驗證本文提出的基于接收機鐘差約束的PPP 時間傳遞方法，選用IGS AMC4、GODE、USN7、BRUX 四個測站的GPS 觀測數據并構成AMC4-BRUX、GODE-BRUX、USN7-BURX 三條時間鏈路進行時間傳遞穩定性分析.

1 接收機鐘差約束的PPP 模型與時間傳遞方法

1.1 PPP 時間傳遞原理

由于非組合PPP 相比于消電離層組合PPP 保留了更多的原始信息且不會增大觀測值噪聲，因此本文基于非組合PPP 模型進行時間傳遞.其原始觀測值的觀測方程[13-14]如式(1)：

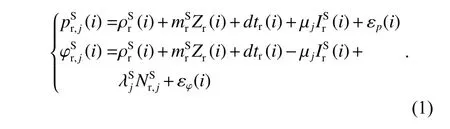
式中：和分別為第i個歷元衛星S到 接收機r 在頻率j上的偽距與相位觀測值；(i)為衛星與接收機間的幾何距離；Zr(i)和mSr分別為測站天頂對流層延遲與投影函數；dtr(i)為接收機鐘差；(i)為第一頻率上的斜電離層延遲；μj=(λj/λ1)2,(j=1,2)為與頻率相關的系數；和分別為j波段的波長與模糊度；εp(i)和εφ(i)分別為偽距與載波觀測值中觀測噪聲、多路徑等未建模誤差.

對于傳統的PPP 時間傳遞方法，接收機鐘差參數dtr(i)通常在濾波過程中被當作WN 參數處理(即不進行歷元間的傳遞)，而本文針對以氫原子鐘提供時間頻率為基準的測站，將接收機鐘差參數建模為隨機游走模型.具體過程為：1)將第i個歷元接收機鐘差的估計值dtr(i)作為第i+1個歷元接收機鐘差的預報值；2)將第i個歷元接收機鐘差估值的方差加上一定的過程噪聲σrclk作為第i+1個歷元接收機鐘差預報值的方差，其中采用的接收機鐘差的過程噪聲σrclk為事先經過大量測站解算得到的經驗方差；3)重復步驟1)和步驟2)進行濾波解算.

1.2 氫原子鐘經驗方差計算

為了充分利用氫原子鐘的高穩定性，本文將歷元間的接收機鐘差約束為隨機游走模型.氫原子鐘先驗方差σrclk計算方法如下：1)首先利用靜態PPP 逐天逐站處理20 個外接氫原子鐘的IGS測站數據，并將接收機鐘差參數視為WN 參數處理得到多個接收機鐘差序列；2)考慮到氫原子鐘的頻率漂移影響，利用Hadamard 方差獲取各測站接收機鐘差序列的先驗方差[15-16]，并取其均值得到氫原子鐘鐘差的過程噪聲經驗方差.

式中：σHDEV(τ)為使用一天的接收機鐘差序列計算得到的Hadamard 方差；τ為數據采樣間隔；c為真空中光速.

1.3 數據處理策略

在文中，由于重點關注接收機鐘差參數在授時以及時間傳遞中的應用，因此在PPP 解算時，將測站固定為IGS 發布的測站坐標軸解值；對流層干延遲部分采用UNB3 經驗模型進行改正，濕延遲部分作為待估參數并按照隨機游走模型估計，投影函數采用全球投影函數(GMF)；接收機鐘差參數作為隨機游走參數進行估計；電離層斜延遲作為WN 參數估計；模糊度參數作為弧段常數估計.其他必要的改正，如天線相位中心改正、天線相位中心變化、相位纏繞等改正也均已考慮.

2 實驗結果與分析

2.1 氫原子鐘先驗方差

基于2019 年第1—90天年積日20 個外接氫原子鐘的IGS 測站得到的接收機鐘差的Hadamard 方差序列如圖1 所示.由圖1 可知，不同方差序列之間的最大差異不超過2mm.所有測站90天的平均方差為1.9mm，標準差為0.23mm，因此不管是同一測站的不同天之間還是不同測站之間，先驗方差序列都是較為穩定的.所以對于任何外接氫原子鐘的測站，只要不發生鐘跳、設備變更等問題，都可以將1.9mm 作為PPP 中氫原子鐘鐘差參數的隨機游走噪聲(RWN).

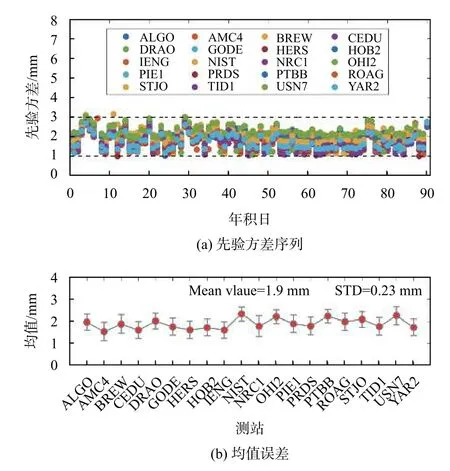
圖1 氫原子鐘測站先驗方差序列

2.2 Hadamard 方差分析

首先，為了分析不同精密鐘差產品對PPP 授時以及時間傳遞穩定性的影響，我們以AMC4 與BRUX 兩個測站為例，采用WUM、GBM、COD、JPL 4 家IGS 分析中心產品分別進行授時和時間傳遞穩定性分析.圖2 為基于上述4 家分析中心精密軌道鐘差產品的PPP 授時頻率穩定性.由于不同分析中心在鐘差估計時選擇的基準不同，衛星鐘差中所包含的基準又會在PPP 解算時被接收機鐘差參數吸收，因此衛星鐘差產品中基準的穩定性會對PPP 授時穩定性產生一定影響.由圖2 可知，使用WUM 與JPL產品可以獲得更高的長期授時穩定性；使用COD 產品可以獲得較高的中期穩定性，不同產品在短期授時穩定性方面差異不明顯.

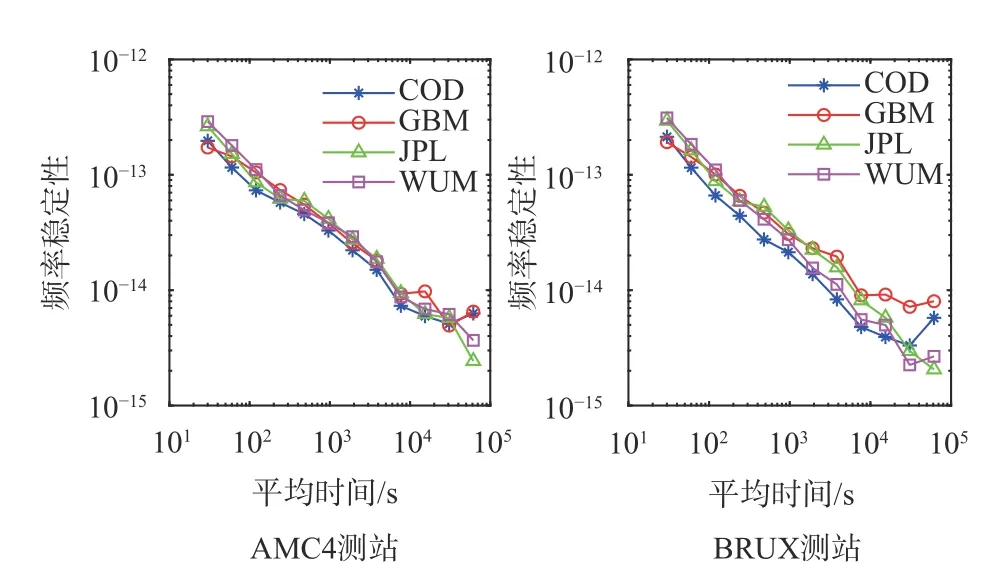
圖2 基于四家分析中心精密產品的PPP 接收機鐘差頻率穩定性

在時間傳遞中，由于要將兩站接收機鐘差進行差分，因此包含在不同精密鐘差產品中的基準會被消除，從而不再影響時間傳遞的性能.圖3 為分析使用不同精密軌道鐘差產品AMC4-BRUX的時間傳遞穩定性.可以看出，使用不同精密產品的時間傳遞穩定性具有較好的一致性，因此衛星鐘差產品的基準不影響時間傳遞的穩定性.

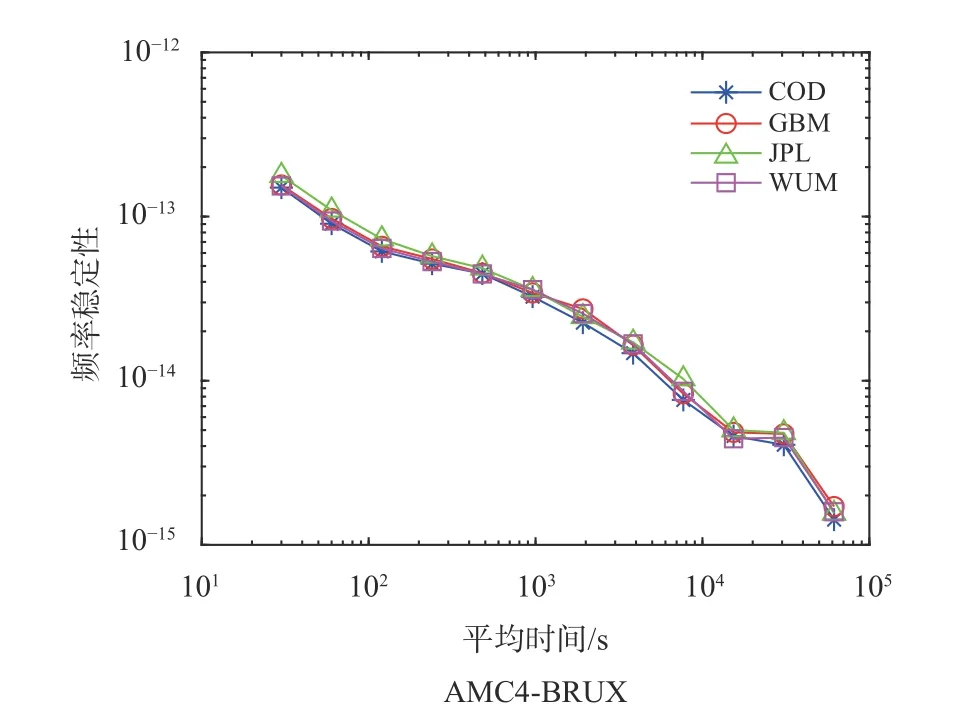
圖3 不同精密產品時間傳遞穩定性

圖4 為2019 年1 月1 日USN7-BRUX 時間鏈路的接收機鐘差之差序列.其中藍色線為傳統的PPP 方法(PPP1 方法)得到的鐘差時間序列，紅色線為基于本文改進的附加接收機鐘差約束的PPP 方法(PPP2 方法)的到的鐘差時間序列.圖5為2019 年1 月1 日USN7-BRUX 時間鏈路中鐘差序列的歷元間差分序列，可以看出，PPP2 方法得到的鐘差序列明顯具有更小的噪聲，因此本文提出的PPP2 方法進行時間傳遞具有更高的穩定性.

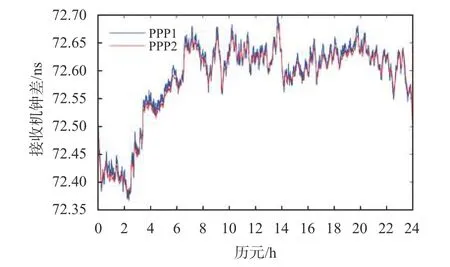
圖4 2019 年1 月1 日USN7-BRUX 時間鏈路鐘差之差序列

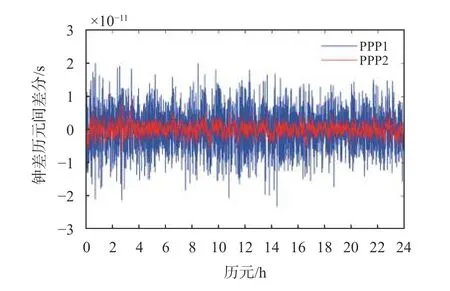
圖5 2019 年1 月1 日USN7-BRUX 時間鏈路鐘差歷元間差分序列

為了從頻率穩定性的角度驗證本文提出的方法在時間傳遞中的性能，我們分析了AMC4-BRUX、CODE-BRUX、USN7-BRUX 三條時間鏈路在2019 年第1—7天年積日的PPP 接收機鐘差的時間序列的Hadamard 方差，其結果如圖6 所示.結合圖6 可知，基于接收機鐘差約束的PPP 時間傳遞相較于傳統的PPP 時間傳遞具有更高的頻率穩定性.其中，本文提出的方法在短期穩定性方面提升最為明顯，可以實現量級上的提升.雖然對于中長期的穩定性提升沒有短期穩定性顯著，但是基于接收機鐘差約束的PPP 時間傳遞方法在時間傳遞穩定性方面始終優于傳統的PPP 時間傳遞方法.

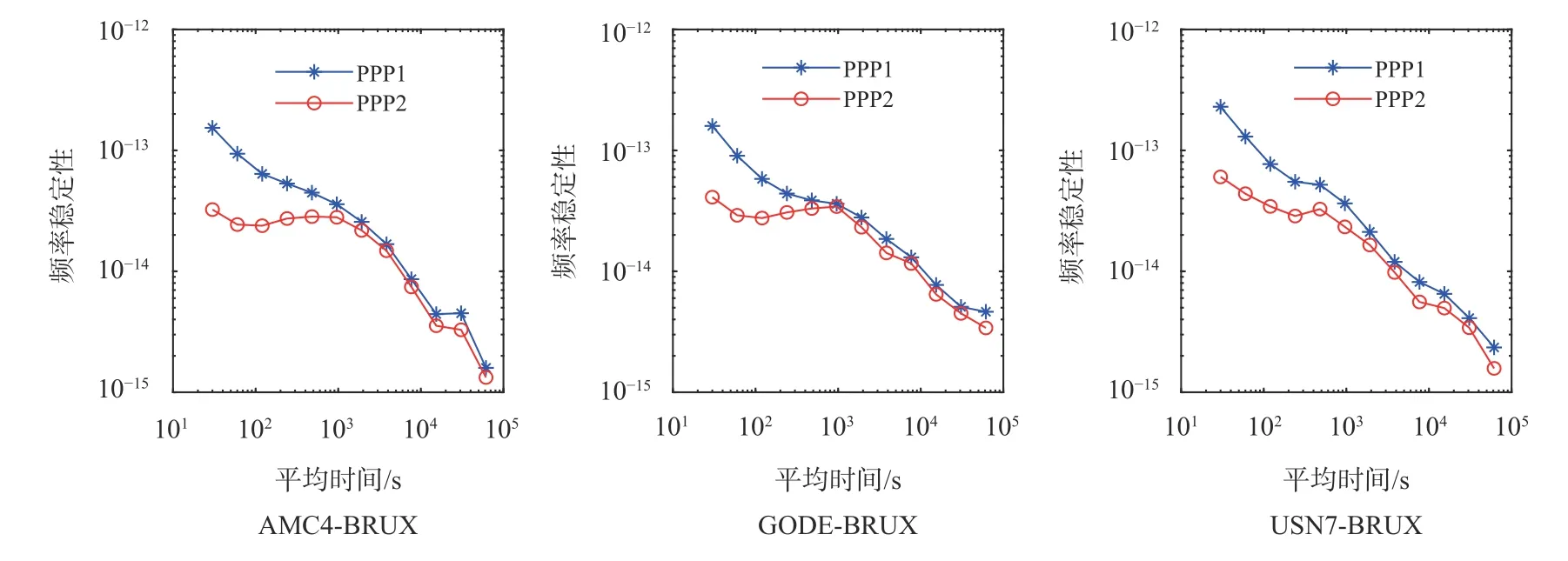
圖6 三條時間鏈路頻率穩定性對比

3 結束語

基于20 個全球分布并配備高精度氫原子鐘30s采樣間隔的IGS 測站數據利用Hadamard 方差得到了氫原子鐘的經驗方差為1.9mm，并在PPP 時間傳遞中將相鄰兩個歷元的接收機鐘差約束為隨機游走模型.通過實驗可知：1)不同精密衛星鐘差產品中的基準會對單站接收機鐘差頻率穩定性產生一定影響，但對于時間傳遞來說，由于其基準可以通過測站間差分被消除，因此衛星鐘差中包含的基準不影響時間傳遞的頻率穩定性；2)對外接氫原子鐘的接收機鐘差經過約束后在短、中、長期穩定性方面均有提升，其中短期穩定性更為明顯，可以實現量級上的提升.