基于低溫啟動特性的PEMFC水熱性能仿真與分析＊

許德超 趙子亮 盛夏 趙洪輝 王宇鵬

（1.中國第一汽車股份有限公司研發總院，長春 130013；2.汽車振動噪聲與安全控制綜合技術國家重點實驗室，長春 130013）

主題詞：質子交換膜燃料電池 冷啟動 水伴熱值 產水速率

1 前言

質子交換膜燃料電池（Proton Exchange Membrane Fuel Cell，PEMFC）因其高效率、高功率密度以及響應快速等特性被認為是在汽車領域最具應用潛力的燃料電池技術之一[1]。目前，影響燃料電池汽車發展的主要障礙包括加氫基礎設施不完善、成本較高和在極寒區域無法使用。在寒冷地區使用受限主要是因為燃料電池冷啟動問題[2]，即電堆在0 ℃以下啟動時，電極反應產生的水在排出電堆前結冰，并進一步導致膜電阻上升、反應物傳質通道堵塞以及反應位置被冰層掩蓋等情況，最終導致冷啟動失敗，甚至性能退化。冷啟動性能的影響因素主要包括電池子部件的材料特性、單體及電堆的結構設計、啟動模式和加載控制策略。水在電池內的結冰會對膜電極組件（Membrane Electrode Assembly，MEA）造成破壞，因此在電池升溫到0 ℃之前控制液態水含量保持在最小值附近是一種合理的思路[3]。

電堆通過自身反應升溫（自熱）實現冷啟動時，需要保證其內部不結冰或者盡量少結冰，以避免可能引起的性能衰減。在電堆自熱升溫期間，其是否結冰以及結冰量顯然與自熱過程中生成的水量相關，而水生成量與電流成正比。此外，電流又與發熱功率相關，因此，控制電堆的水生成量，并最大化內部發熱功率成為自熱冷啟動成功的核心。

為了更好地說明上述相關性，本文引入水伴熱值的概念，即生成單位質量水所產生的熱量，并進行3D仿真計算，以期為冷啟動控制策略的制定提供參考。

2 仿真模型描述

2.1 模型說明

本文采用多物理場仿真軟件Comsol 5.4 進行建模計算。在模型中主要求解的未知變量有電位φs、離子勢φ1、陽極氫質量分數w(H2)、陽極水質量分數wa(H2O)、陰極氧氣質量分數w(O2)、陰極水質量分數wc(H2O)、陰極氮氣質量分數w(N2)、陽極和陰極中的速率場矢量ua和uc、陽極和陰極中的壓力pa和pc以及總發熱功耗密度Qh。

模型通過耦合2個“反應流”接口和1個“二次電流分布”接口來實現求解。

在求解電化學電流方面，二次電流分布接口基于歐姆定律對電化學電流進行建模，求解氣體擴散層（Gas Diffusion Layer，GDL）中的電位、多孔電極中的電位和離子勢，以及電解質膜中的離子勢。在多孔電極中，局部電流密度取決于離子勢和電勢，但也受反應物局部濃度的影響。

在陽極，氫氧化反應為：

隨濃度變化的線性巴特勒-褔爾默（Butler-Volmer）表達式可用于陽極局部電流密度ia的計算：

式中，i0,a為陽極交換電流密度；c(H2)為局部氫濃度；cref(H2)為氫參考濃度；αa,a為陽極傳遞系數；αc,a為陰極傳遞系數；F為法拉第常數；R為氣體常數；T為開氏溫度；ηa為陽極活化極化電壓。

在陰極，氧氣與質子發生反應，形成水，反應式為：

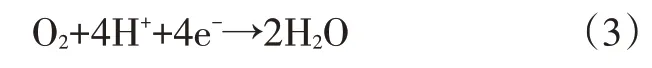
陰極氧還原反應的局部電流密度ic為：

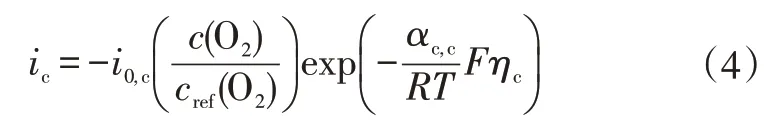
式中，i0,c為陰極交換電流密度；c(O2)為局部氧濃度；cref(O2)為氧參考濃度；αc,c為陰極傳遞系數；ηc為陰極活化極化電壓。

式（4）是隨濃度變化的簡化Butler-Volmer 表達式，已忽略陽極項，也可以看作隨濃度變化的塔菲爾（Tafel）方程。

設與陽極GDL接觸的流道脊板位置電位為0，與陰極GDL 接觸的流道脊板邊界電位為電池的輸出電壓Vcell，所有其他外部邊界都設置為絕緣。

求解質量傳遞方面，在2個不同的“濃物質傳遞”接口中使用Maxwell-Stefan 方程求解流道、GDL 和多孔電極中的w(H2)、wa(H2O)、w(O2)、wc(H2O)和w(N2)。對于陽極，求解氫氣和水；對于陰極，求解氧氣、水和氮氣。

通過質量源和匯，將這2個接口與“二次電流分布”接口耦合。

在流道入口處指定了質量分數，在流道出口處使用流出條件。所有其他外部邊界都使用零通量條件。

對于求解動量傳遞，借助“Brinkman 方程”接口；對于流道，通過納維-斯托克斯（Navier-Stokes）方程對速度u和壓力p進行建模；對于多孔GDL 和電極（Catalyst Layer，CL），通過Brinkman方程進行建模。

通過使用“反應流”多物理場節點，將“Brinkman 方程”接口與“濃物質傳遞”接口耦合，實現密度、速度、壓力、凈質量源、質量匯以及物質傳遞的耦合。

在流道入口邊界，指定入口流速分布為層流流入，出口處指定壓力邊界條件。為了對多平行通道的情況進行建模，沿GDL 和多孔電極的長邊應用對稱邊界條件。所有其他壁邊界都應用了無滑移邊界條件。

在此過程中可以同時求解出電池內部各組件的熱功耗密度分布，包括歐姆極化、活化極化和濃差極化引起的熱功耗。對熱功耗密度Qh在電化學域內進行積分可得到電池的總發熱功率Ph。

陰極生成水的速率Δm(H2O)可通過法拉第定律進行計算：

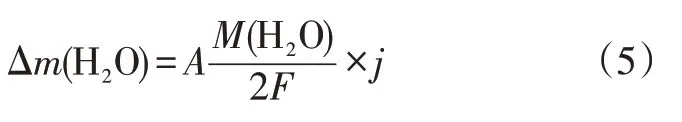
式中，A為MEA 的活性面積；M(H2O)為水的分子量；j為電流密度。

則水伴熱值Q(H2O)為總發熱功率Ph與產生水速率Δm(H2O)的比值：

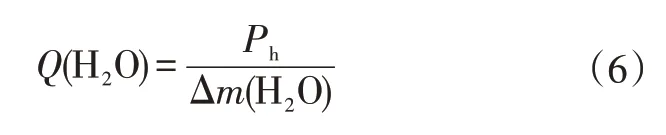
計算過程中用到的主要參數如表1 所示。本文計算了在相同空氣流速Uin_ca、不同輸出電壓Vcell（0.05～0.80 V）下以及在相同輸出電壓Vcell（0.2 V）和不同空氣流速Uin_ca下（對應不同計量比Ca.S.R.）的電池發熱功率分布情況以及水伴熱值。

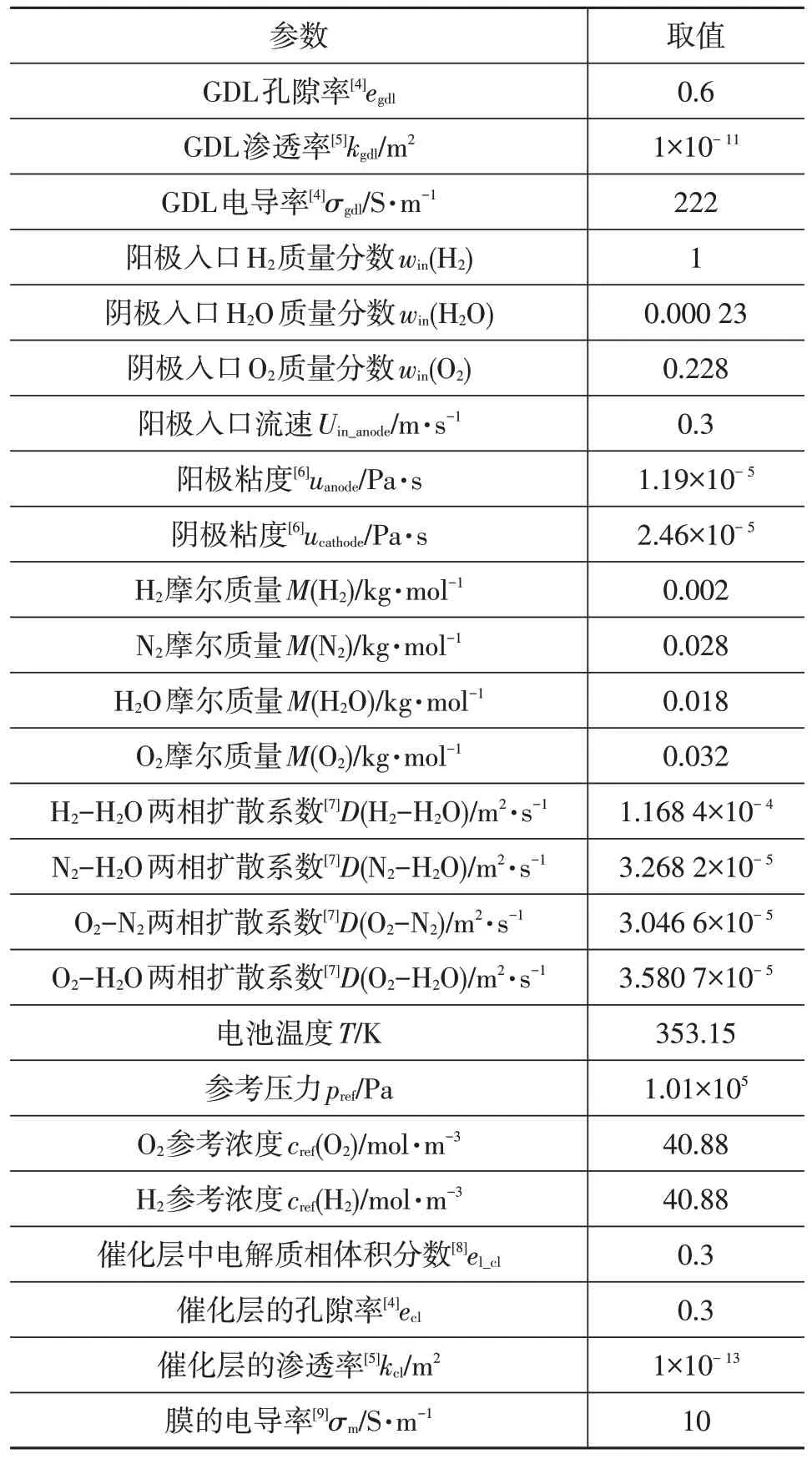
表1 主要參數取值

2.2 前提假設

為簡化模型求解，本文進行以下假設：

a.氣體和混合物為理想氣體，且符合菲克定律；

b.電池溫度為恒定值，且忽略極化熱等參數受溫度變化的影響；

c.電池內部氣體流動為層流；

d.膜和催化層是各向同性和均勻的；

e.由于本文是基于低溫啟動特性評估進行的仿真，而非對冷啟動過程進行仿真，因此，假設在其他條件不變的條件下，水伴熱值Q(H2O)越大，冷啟動成功率越高；

f.因為針對冷啟動過程的瞬態仿真尚不成熟且精度較低，這里采用穩態計算，不考慮膜離子電導率受水含量變化的影響，且不考慮電池中各物理量的瞬態變化；

g.不考慮氫氣和空氣在膜兩側的滲透情況。

2.3 幾何尺寸

圖1給出了單流道PEMFC模型的3D幾何結構。該模型包括陽極流道、陽極GDL、陽極催化層（Anode Catalyte Layer，ACL）、膜、陰極催化層（Cathode Catalyst Layer，CCL）、陰極GDL 和陰極流道，共7 個域。幾何參數參考實際電池尺寸取值，如表2所示。

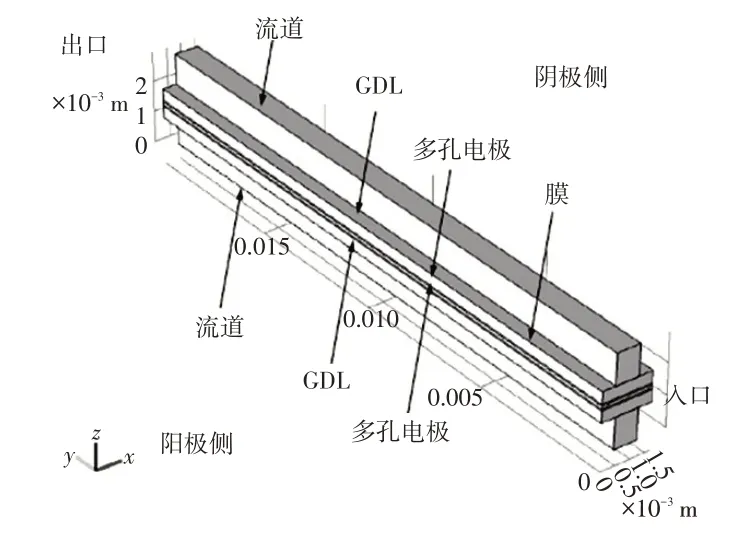
圖1 模型的幾何結構

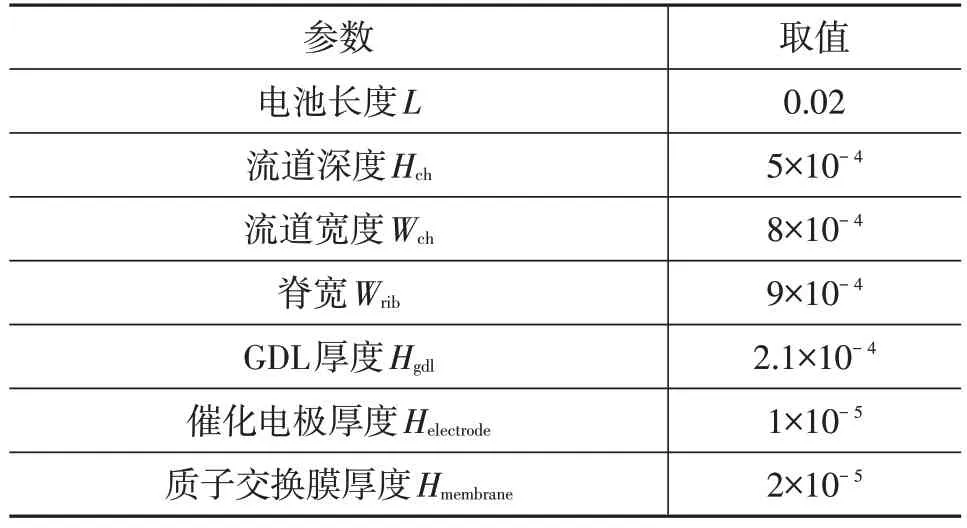
表2 幾何參數 m

3 計算結果與數據分析

3.1 熱源種類及發熱功率占比

燃料電池內部的總熱源Ph主要分為陰極極化熱Pca、陽極極化熱Pan和歐姆熱Pohm3 個部分，歐姆熱主要考慮兩側GDL層和質子交換膜中電子和離子傳導產生的熱。在相同輸出電壓和不同陰極計量比下，3種熱源發熱功率的計算結果如表3所示。

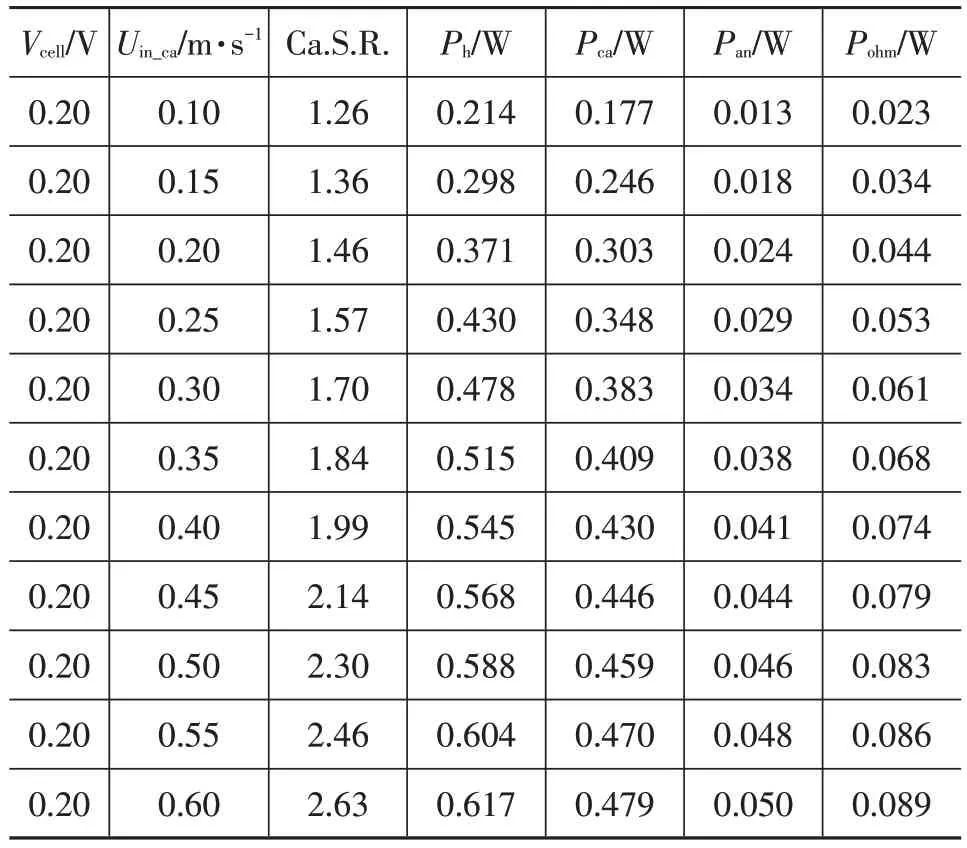
表3 相同輸出電壓和不同陰極計量比下熱源與發熱功率

從表3 中可以看出，在陰極計量比為1.99 時（接近實際值），0.2 V 電位下該電池的整體發熱功率約為0.545 W，其中陰極催化層發熱功率占比79.6%，陽極催化層發熱功率占比7.4%，而分布在質子交換膜和GDL層中的歐姆發熱功率占比13.0%。由此可見，產熱主要集中在陰極催化層區域，這與陰極氧還原反應本身反應速率較低是一致的。同時，也可以看出這種發熱情況有利于低溫啟動，因為陰極催化層也是水首先出現的位置。

圖2 給出了分熱源發熱功率隨陰極計量比的變化情況，可以看出，隨著陰極計量比的提升，總發熱功率不斷變大，這意味著電堆將會升溫更快，啟動速度也會更快。陰極催化層的發熱功率也隨之增加，但增加速率趨緩。

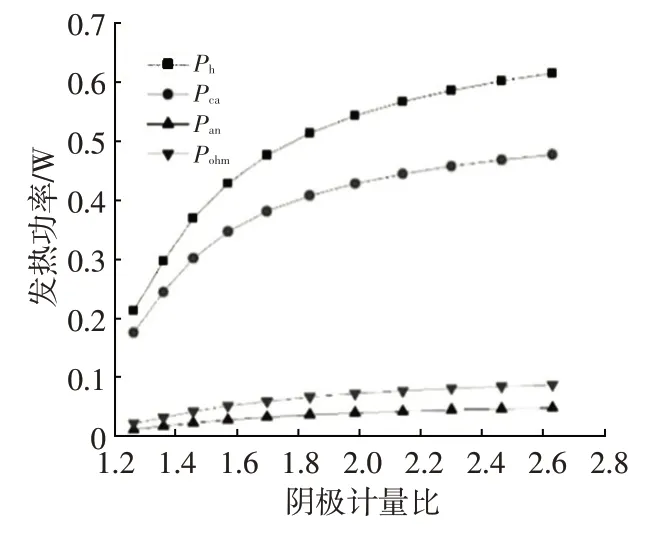
圖2 分熱源發熱功率隨陰極計量比變化情況

3.2 陰極催化層發熱功率分布

在燃料電池發熱功率中，陰極催化層占比最高，因此重點考慮陰極催化層的熱量分布情況。圖3 給出了陰極催化層發熱功率密度分布隨陰極計量比的變化情況。可以看出，計量比越低，發熱功率分布越不均勻，熱量主要集中在陰極入口附近區域，在計量比為1.26時，發熱功率密度最高值與最低值相差達到6 個數量級。而最低發熱功率密度通常出現在陰極出口附近和兩側脊下區域。

當計量比提升至2.63 時，發熱不均的情況明顯得到改善，發熱功率密度最高值和最低值相差約3個數量級，此時入口和出口之間的差別已經不大，低發熱功率密度主要出現在脊下區域。可見，在冷啟動過程中，脊下區域發熱功率密度普遍較低，該部分也最容易發生結冰。

在冷啟動過程中，通常根據工況控制單體輸出電壓值以實現成功啟動。本文對相同流量下不同輸出電壓時陰極催化層的發熱功率密度分布進行了計算，結果如圖4所示。可以看出，當電壓低至0.1 V時，電池內部的發熱情況極端不均勻，發熱功率密度最高值與最低值相差達到9 個數量級，這種情況對燃料電池各零部件，尤其是雙極板和GDL 層的導熱能力要求很高。從圖4 中還可以看出，當輸出電壓較高時，脊下位置的發熱功率明顯得到改善。這種現象也可以為冷啟動控制策略的制定提供一定參考。

圖3 不同陰極計量比下的陰極催化層發熱功率密度分布

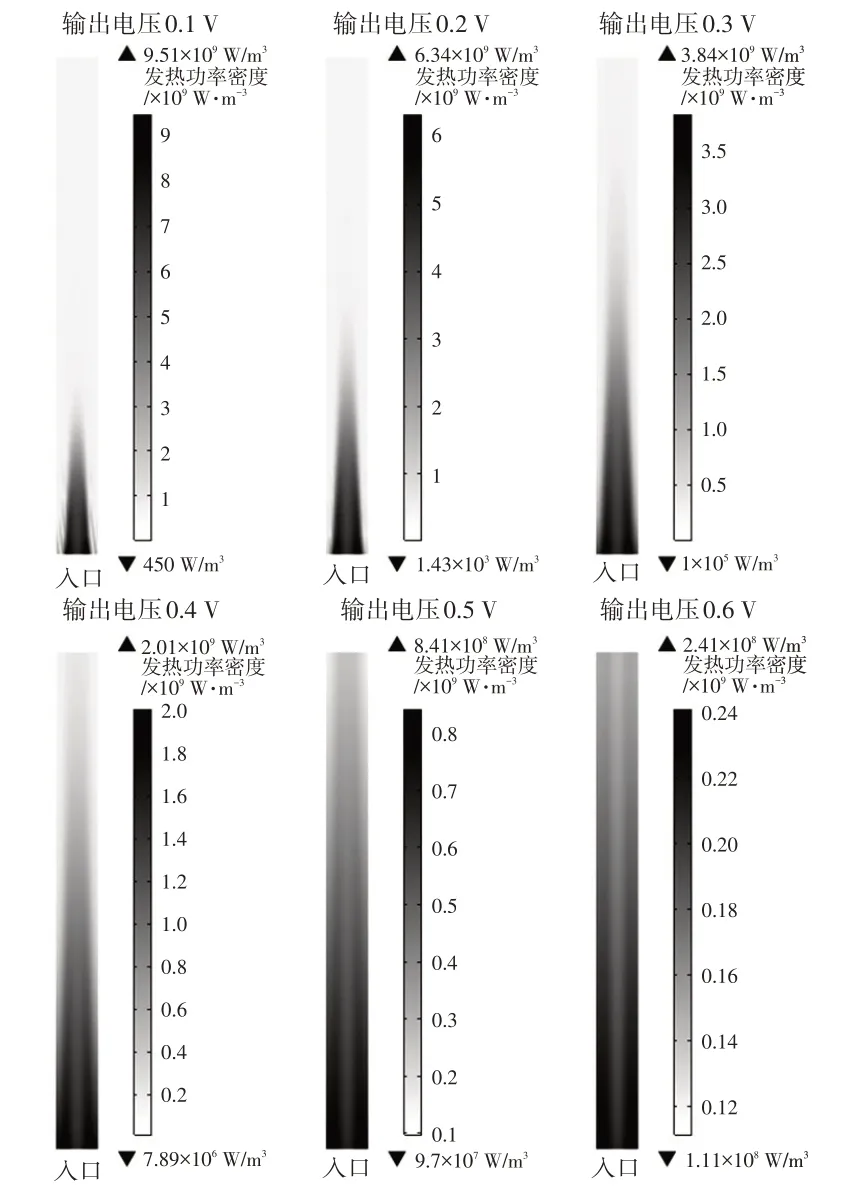
圖4 相同流量不同輸出電壓下陰極催化層的發熱功率密度分布

3.3 水伴熱值

表4給出了在相同流量、不同輸出電壓下電池內部工作狀態的計算結果。包括總發熱功率、產水速率、水伴熱值等指標。

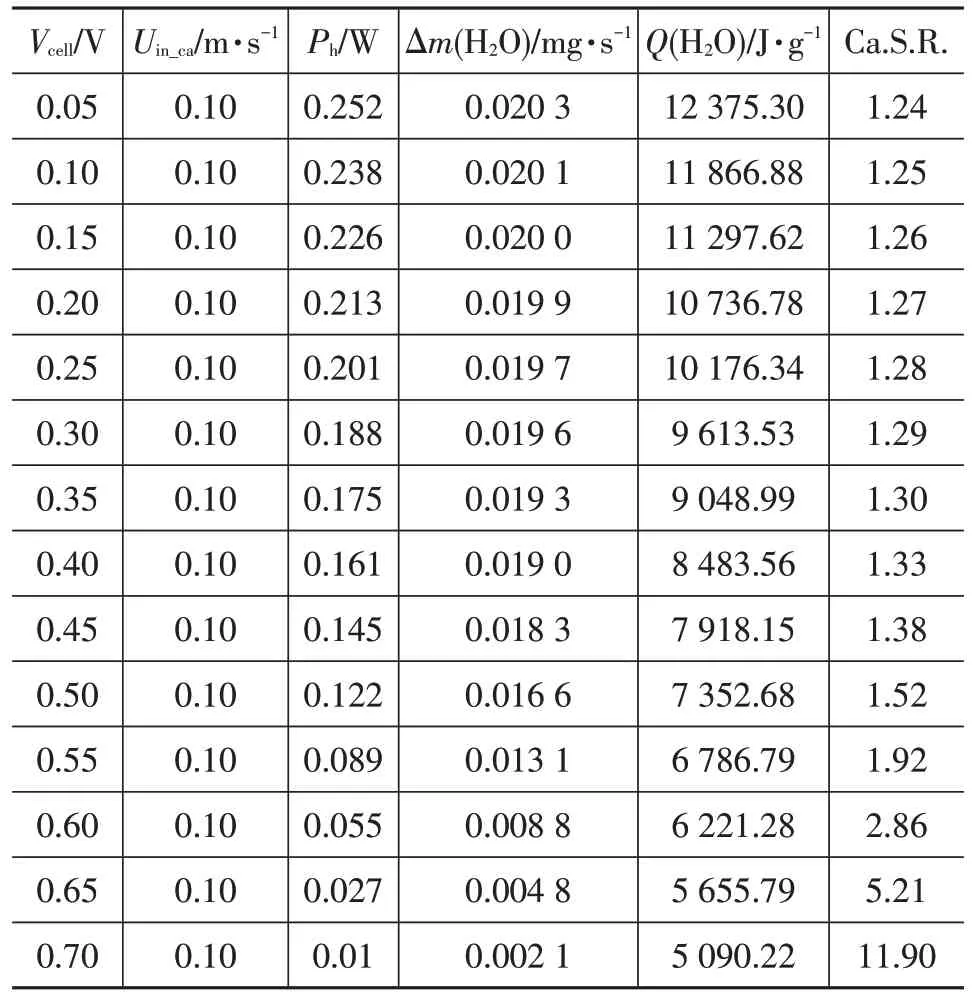
表4 相同流量不同輸出電壓下電池內部工作狀態計算結果

從表4 中可以看出，每生成1 g 水，當輸出電壓為0.1 V 時，燃料電池內部能夠產生的熱量是輸出電壓為0.6 V時的約2倍。

根據表4中數據，對水伴熱值隨輸出電壓的變化情況進行作圖，如圖5 所示。可以看出，隨著輸出電壓的升高，生成單位質量水產生的熱量呈線性減少，這說明可以通過控制輸出電壓的方式在保持生成水量不變的條件下提高產生的熱量，這也是冷啟動過程中面臨的核心問題。輸出電壓越低，水伴熱值越高，這是因為燃料電池發電效率降低導致了更多的化學能轉化為熱能。

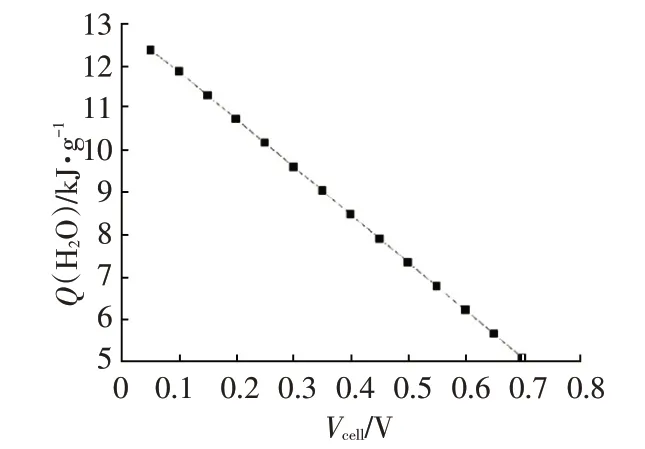
圖5 水伴熱值隨輸出電壓的變化曲線

為考察計量比對水伴熱值的影響情況，對其進行計算，結果如表5 所示。根據表5 中數據，對水伴熱值和水生成速率隨陰極計量比的變化情況進行作圖，如圖6 所示。可以看出，在特定輸出電壓下，計量比的變化基本不會影響水伴熱值的變化。然而，生成水的速率Δm(H2O)隨著陰極計量比的增加而增加，這意味著可以通過控制陰極計量比來控制電池在冷啟動過程中的產水速率。

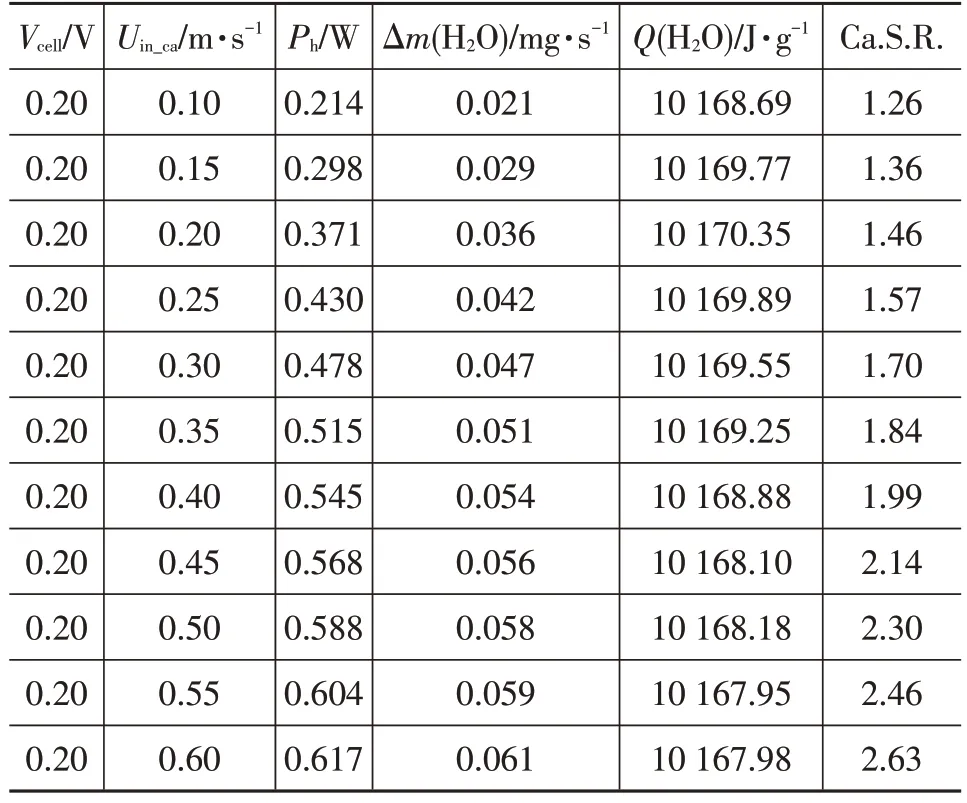
表5 相同輸出電壓不同陰極計量比下電池內部工作狀態計算結果

圖6 水伴熱值和水生成速率隨陰極計量比的變化曲線

4 結束語

本文采用Comsol 軟件建立了質子交換膜燃料電池3D 仿真模型，對不同輸出電壓和計量比下電池內部的熱源發熱功率占比、陰極催化層的發熱功率密度分布情況進行了計算，并引入水伴熱值概念，深入探討了如何在控制產水量的同時，最大限度提升燃料電池的發熱功率以提高冷啟動的成功幾率。

計算結果表明：燃料電池內部產熱主要集中在陰極催化層區域，且該區域產熱的占比隨陰極計量比的降低而升高，同時，計量比越低催化層內發熱功率分布越不均勻；可通過拉低輸出電壓來提升水伴熱值，當電壓從0.6 V 降低至0.1 V 時，相同產水速率下，總發熱功率可提升約1 倍；在特定輸出電壓下，計量比的變化基本不會影響水伴熱值的變化，但生成水的速率隨著陰極計量比的增加而增加。

綜上，在冷啟動控制策略制定時，可通過適時控制陰極計量比和輸出電壓達到提高水伴熱值、控制熱源占比、發熱分布和產水速率的效果；在雙極板和MEA等材料選型時，考慮電化學性能和熱質量的同時也要重視對熱傳導系數和耐熱性的考慮，以應對冷啟動過程中發熱極為不均的情形。