基于激光雷達點法向量的車輛實時位姿估計*
張瑞賓 郭應時 陳元華 劉曉剛 周揚
(1.長安大學,西安 710064;2.桂林航天工業學院,桂林 541004)
主題詞:激光雷達 運動車輛 點法向量 位姿估計
1 前言
智能車輛通過激光雷達等環境感知系統對運動車輛位姿(Moving Vehicle Pose,MVP)進行準確估計,可有效提高危險交通場景下的安全性。國內外學者針對運動物體的位姿展開了相關研究。王巖等人[1]提出了一種基于迭代最近點(Iterative Closest Point,ICP)的井下無人機實時位姿估計方法,將煤礦井下四旋翼無人機位姿估計問題轉換為機載激光點云數據的掃描匹配問題。宋亮等人[2]提出了基于擴展卡爾曼濾波(Extended Kalman Filter,EKF)的相對位姿估計算法,對相對位置和姿態進行估計的同時,可辨識出目標的未知參數。郝剛濤等人[3]提出一種基于單目相機與無掃描三維激光雷達融合的非合作目標相對位姿估計方法,可實現尺度模糊下相對位姿的快速魯棒估計。暢春華等人[4]提出一種基于二維激光雷達的移動機器人實時位姿估計算法,通過優化位置序列間的方向角實現機器人的位姿估計。S.Akshay 等人[5]提出了一種基于無人機周圍點云特征的激光雷達定位誤差協方差矩陣自適應估計方法,該方法比基于距離的協方差矩陣模型更精確。Opromolla等人[6]提出了基于在軌服務的激光雷達三維點云姿態估計算法,通過姿態跟蹤算法對姿態進行校正,通過將模型點云和目標點云進行ICP 匹配實現姿態跟蹤。Y.Fang等人[7]提出了全等四面體對齊(Congruent Tetrahedron Align,CTA)算法,通過激光雷達掃描點云和模型點云中的全等四面體確定相對位姿,采用ICP算法進行CTA后的姿態跟蹤。N.Philip等人[8]提出了基于相平面控制技術的相對位置控制和基于相對四元數反饋的相對姿態控制方法,證明了固定增益觀測器對位置和姿態的估計是有效的。
以上位姿估計方法在點云幾何信息較完整、分布特征顯著時是可行的。但由于激光雷達掃描視場有限,每幀僅能獲取單一視角下的場景,導致點云數據存在遮擋殘缺等現象,獲取目標表面采樣點數量取決于激光雷達與目標間的相對位置,從而影響位姿估計準確率。因此,本文提出一種基于點法向量特征的方法,以解決動態剛性目標點云殘缺導致位姿信息難以提取的問題。
2 基于點法向量的目標姿態估計算法
2.1 算法的提出
在傳統位姿估計算法中,要求模型庫具有較大樣本數量,且待測目標三維點云數據具有較高完整性,為了減少算法對以上條件的限制,基于目標車輛表面所具有的剛性特點,結合車載激光雷達采集運動目標車輛點云數量隨距離變化的特性,本文提出基于點法向量的動態車輛實時位姿估計方法,流程如圖1所示。
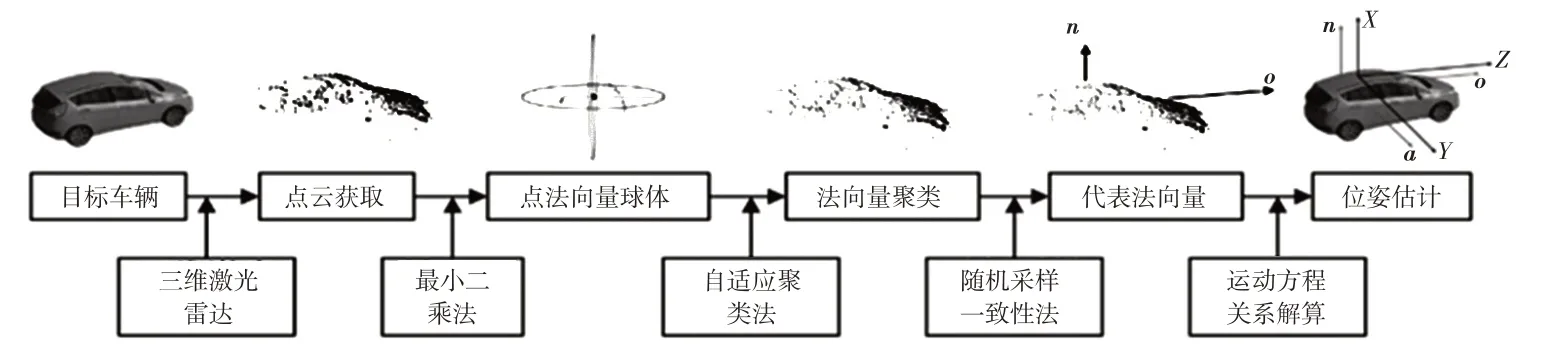
圖1 算法流程
2.2 點云數據的獲取
車載激光雷達安裝位置如圖2所示,在車輛縱向中心平面上,A點位于車輛背門最高處,B點位于發動機罩最前端,C點和D點分別為A柱在縱向中心平面投影處的最高點和最低點,F點為車載激光雷達的幾何中心。取A點在地平面的投影點O作為坐標系原點,以O為起點,在縱向中心平面內沿地平面指向車頭為X軸正方向,過點O垂直縱向中心平面指向駕駛員側為Y軸正方向,過點O垂直地平面指向車身為Z軸正方向。A′與A′′、B′與B′′、C′與C′′分別關于A、B、C點對稱。激光雷達中心坐標為(x0,y0,z0),其輪廓底部投影對應直線llow,安裝激光雷達時,為了保證點云采集的對稱性,應將雷達置于車頂中心處,且確保其工作時不會掃描到車身(即關鍵點A、B、C、D),即滿足:
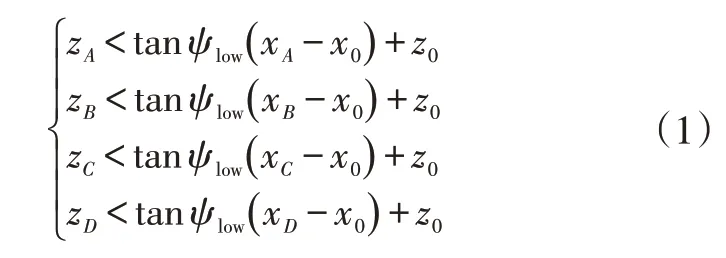
式中,ψlow為垂直視場角;zA、zB、zC、zD、z0分別為A、B、C、D、O點的z坐標;xA、xB、xC、xD、x0分別為A、B、C、D、O點的x坐標。
選用速騰聚創公司RS-LiDAR-32 型激光雷達,該激光雷達可實現垂直視場角-25°~15°、水平視角360°掃描周圍環境,測距最大范圍200 m,每秒輸出64×104個點,設置掃描頻率為20 Hz。
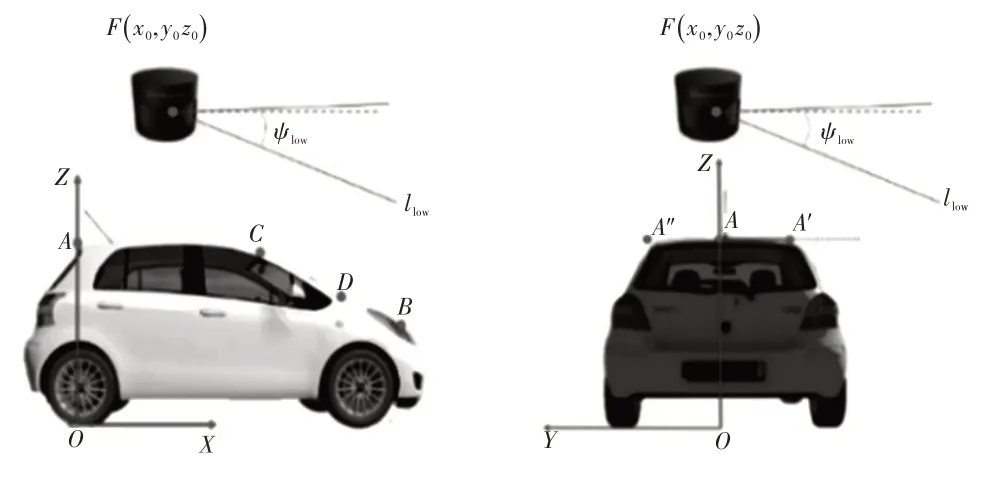
圖2 車載激光雷達安裝示意
2.3 平面點的判定及點法向量估計
本文通過剛性目標表面局部擬合平面上的點法向量進行姿態估計,以彎曲度特征濾除非平面上的點法向量。表面點云任意點P的彎曲度CP滿足:
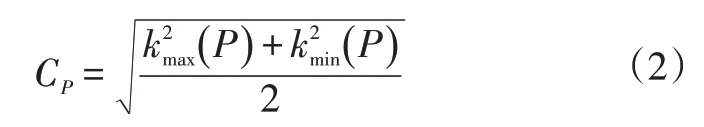
由式(2)可知:當CP近似為0或小于一定的閾值時,可判定P點為平面點;當CP大于一定的閾值時,可判定P點為非平面點。該閾值可依據實際點云中的噪聲及其他誤差影響確定。
2.4 自適應聚簇中心的點法向量分類方法
利用最小二乘法擬合求得目標車輛三維點云各點的法向量后,由于車輛屬于剛性物體,表面由不同角度的近似平面組成,各表面估計的點法向量的方向不同,因此需要對全部點法向量進行聚類分析。傳統的Kmeans 算法的聚簇數量k是根據經驗事先人為設定的,由隨機方式確定初始聚類中心,車載激光雷達采集周圍運動車輛點云數據的角度實時發生變化,復雜場景下目標物間存在遮擋問題,導致獲取目標點云平面的數量存在差異,聚簇數量應與獲取的平面數量相關聯,應采用自適應聚簇中心的聚類算法流程確定聚簇數量,算法自適應性主要體現在根據目標點云質心向量與點法向量之間的夾角分布來自適應求取k和各聚簇中心值c(k)。算法具體步驟為:
a.求取車輛目標點云坐標原點指向質心的向量C;
b.求取每個點法向量與C之間的夾角θi;
c.求取θi分布直方圖,如圖3 所示,篩選出頻數f大于閾值λ的點法向量分布區間種類數量即為聚簇數量k;
d.求取所篩選出的各類分布區間內的點法向量數量;
e.求取每類點法向量均值,得到c(k);
f.求取標準測度函數,評價其收斂性,得到最大迭代次數后停止,否則,循環a~e。最終得到點法向量聚類結果如圖4所示。
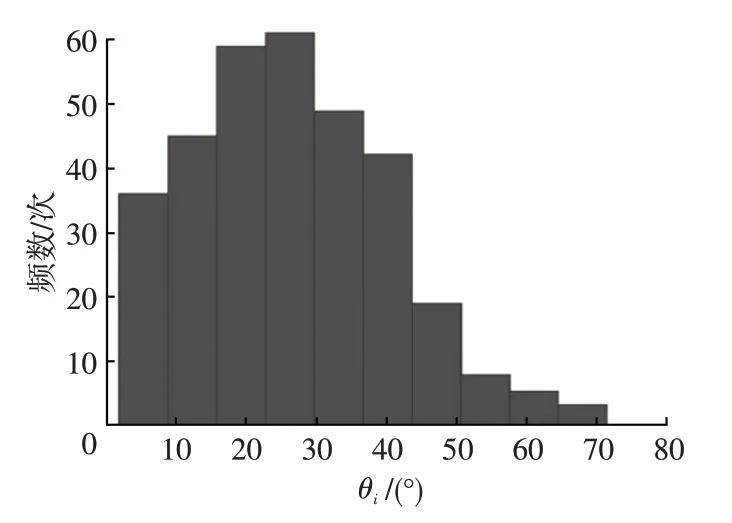
圖3 θi分布直方圖
2.5 坐標軸的確定
由于復雜場景下聚類獲得的點云數據受到噪聲和遮擋因素的影響,點云并不集中在某一平面內,導致待擬合平面的點法向量分布不均勻,因此應選取抗噪性能較好的隨機采樣一致性(Random Sample Consensus,RSC)算法對聚類后的點進行二次處理。
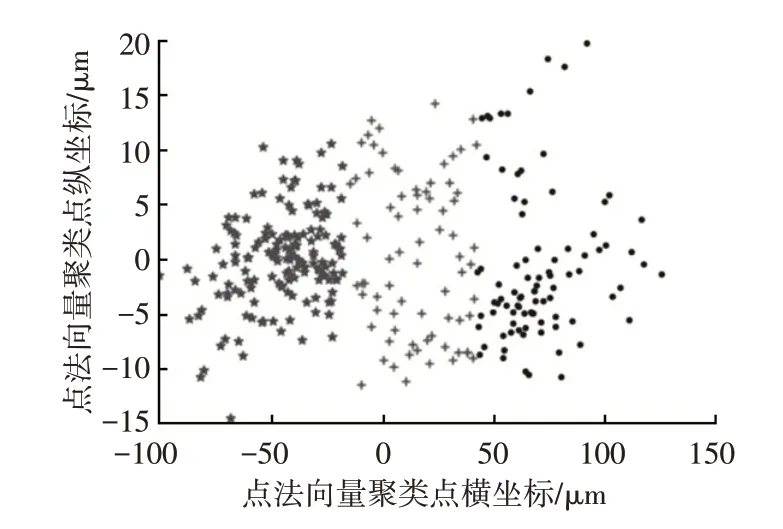
圖4 點法向量聚類結果
RSC算法先從樣本集合中隨機抽取一個樣本子集,采用最小方差估計算法計算該子集模型參數,對比樣本與模型間的偏差,利用預先設定的閾值與偏差比較,當偏差小于等于閾值時,該樣本點被定義為內點(Inliers),否則為外點(Outliers)。RSC 可以剔除外點的影響,最終得到全局最優的參數估計值。RSC算法的關鍵在于確定閾值d、迭代次數K[9]:
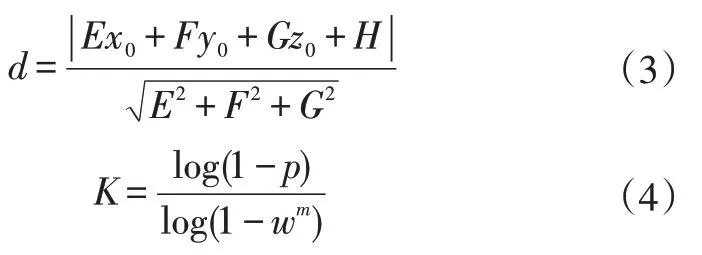
式中,E、F、G、H為常量;p為置信度;w為內點在數據集內的占比;m為計算模型最小樣本數量。
算法具體步驟為:
a.從待擬合的點云集合中隨機選取3 個點,計算其構成的擬合平面方程z=ax+by+c;
b.計算點云中各點至該平面的距離di=|axi+byi+zi|;
c.利用式(3)計算出閾值d,當di≤d,判定該點為內點,并統計內點數量;
d.利用式(4)計算迭代次數K,通過迭代運算統計出最多數量的內點集合,并對該情況下獲取的內點進行平面擬合。
圖5 所示為采用目標車輛表面點云擬合的平面點法向量,由圖5 可知,三維點云場景下的待測目標坐標系中X軸和Z軸即為剛性物體所占比重最大的2類點云垂直擬合平面的代表點法向量n和o,Y軸可通過n和o叉積的形式獲得,目標車輛表面擬合平面點法向量與OXYZ坐標系的關系如圖6所示。
2.6 目標姿態的求取
確定出擬合平面代表法向量n(nx,ny,nz)、o(ox,oy,oz)、a(ax,ay,az)后,通過歐拉角旋轉矩陣對運動目標的橫滾角?、俯仰角θ和航偏角ψ進行解算:

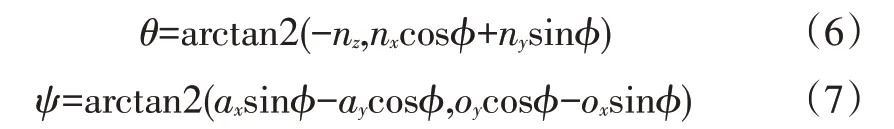
由式(5)~式(7)解算出的(?,θ,ψ)即為目標物三維姿態角。
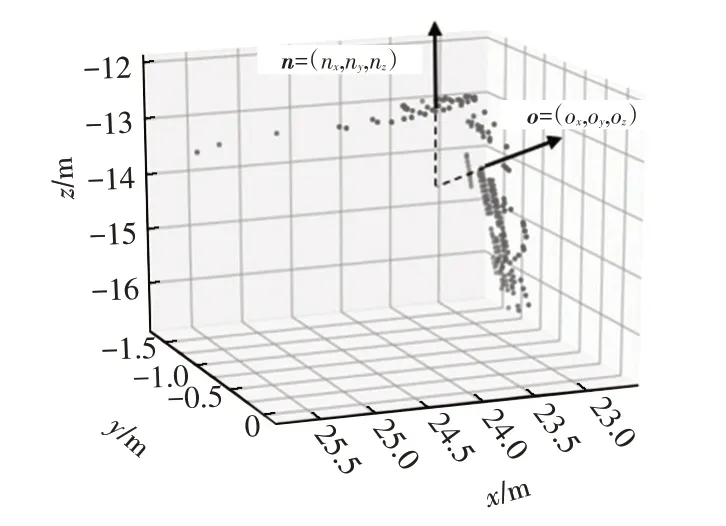
圖5 目標車輛表面點云擬合的平面點法向量
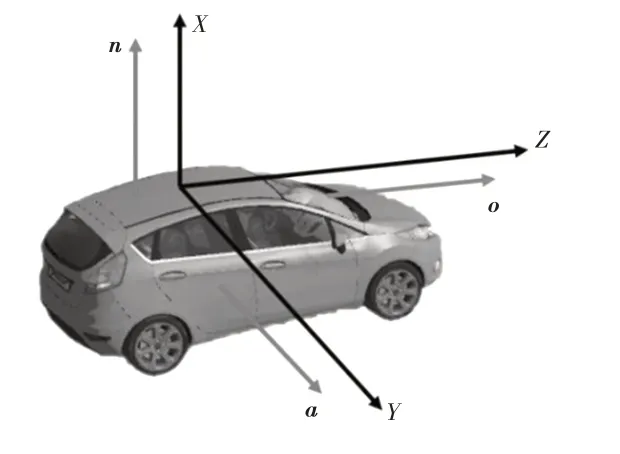
圖6 擬合平面點法向量與OXYZ坐標系的關系
3 姿態估計算法試驗
為了定量地分析所提出的動態車輛實時姿態估計算法的效果,利用試驗車采集某城市復雜交叉口點云數據,結果如圖7 所示,該車頂部裝配有三維激光雷達。激光雷達以10 幀/s 的掃描幀率,獲得目標車輛運動時車輛運動點云圖,如圖8所示。采用基于點法向量的動態車輛實時位姿估計方法,得到如圖9所示的連續位姿估計結果,通過計算車輛質心點處點法向量位置變化,實時估計車輛位姿。

圖7 試驗車采集的某城市復雜交叉口點云數據
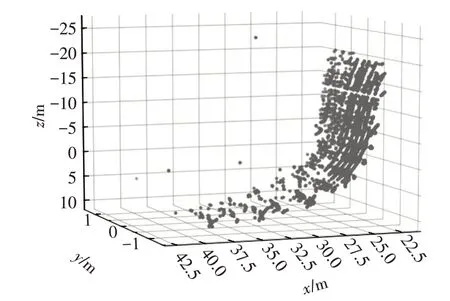
圖8 激光雷達連續幀掃描目標車輛點云
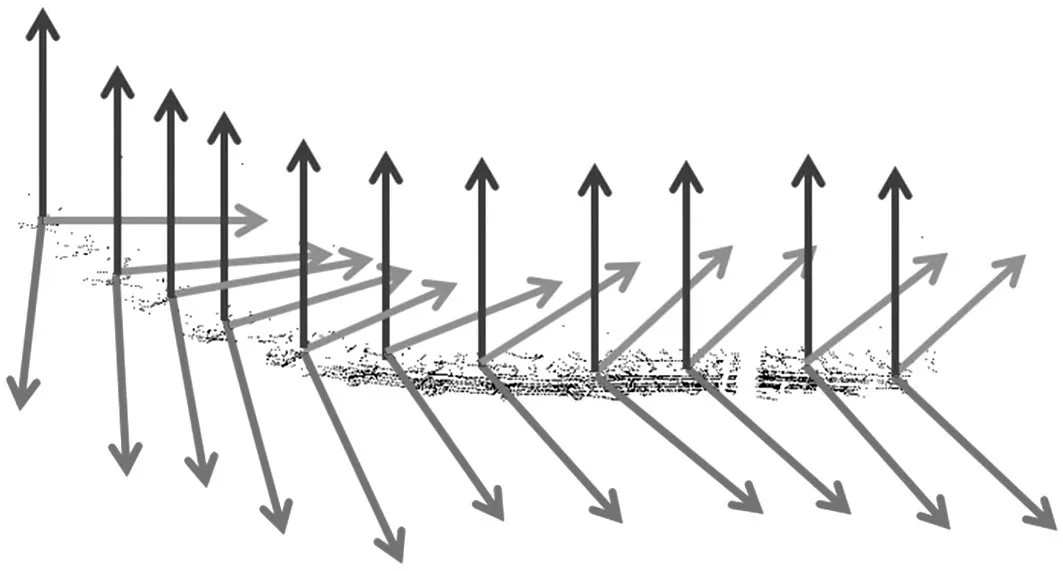
圖9 連續位姿估計結果
為了驗證算法的有效性,采用均方根誤差(Root Mean Square Error,RMSE)R衡量觀測值與真值之間的偏差。R越小,代表位姿估計的測量精度值越高:

式中,Xobs,i、Xreal,i分別為目標車輛第i幀時點云對應的位姿估計值和真實值。
圖10、圖11所示分別為目標車輛經過交叉口時,直線運動和曲線運動狀態下的實際運動軌跡與試驗車實時獲取的目標車輛質心坐標點間的偏差關系,圖中所示車輛質心點位置與實際運動軌跡具有一定的擬合度,因此可以通過計算質心點處點法向量實時估計車輛位姿。
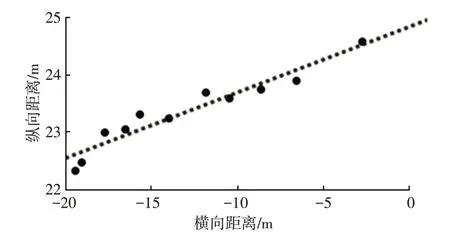
圖10 直線運動軌跡與質心點位姿坐標偏差關系
由圖7 可知,當目標車輛通過某城市交叉口時,運動軌跡主要由直線軌跡和曲線軌跡組成,表1所示為目標車輛實時位姿估計RMSE分析結果。
由表1 可知:目標車輛直線運動時,基于點云法向量的方法計算得到的運動目標車輛橫滾角?、俯仰角θ和航偏角ψ的均方根誤差較低,且均小于傳統迭代最近點方法;曲線運動時,由于目標車輛方向角變化較大,造成點云數據遮擋殘缺現象較為嚴重,基于點云法向量的方法計算得到的?、θ和ψ的均方根誤差值均高于直線運動的均方根誤差值,但仍小于傳統迭代最近點方法。因此,當目標車輛通過某城市交叉口時,在直線和曲線2種軌跡運動情況下,基于點云法向量算法對目標車輛的位姿估計效果均優于迭代最近點算法,且受點云數據遮擋殘缺現象的影響程度均低于傳統迭代最近點算法。
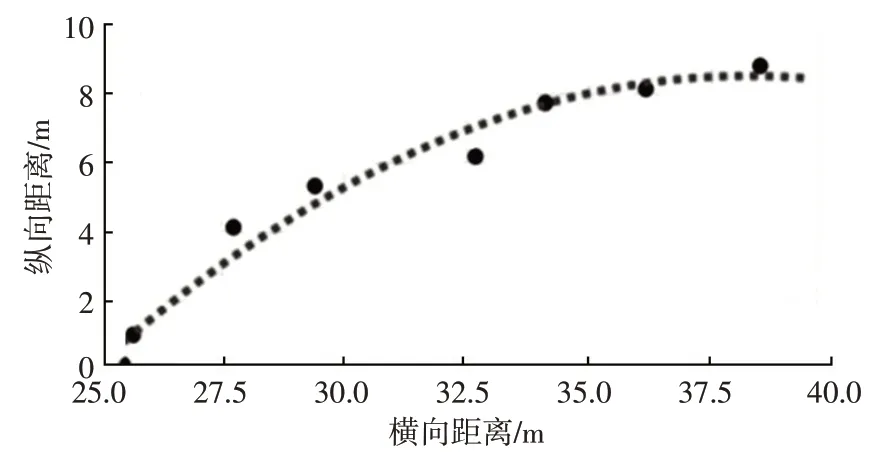
圖11 曲線運動軌跡與質心點位姿坐標偏差關系
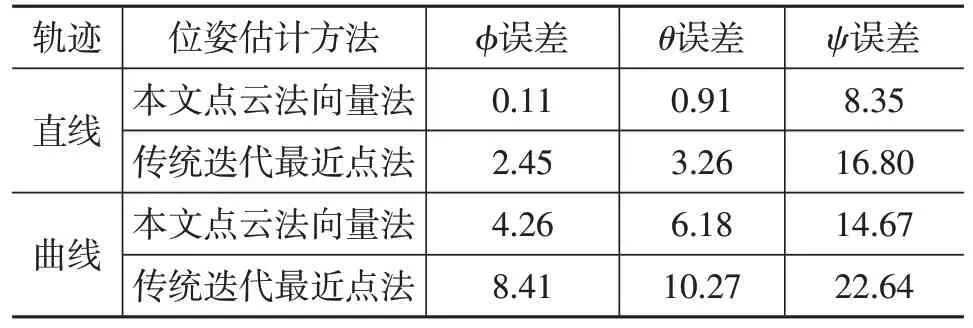
表1 目標車輛運動實時位姿估計RMSE分析結果 (°)
三維姿態估計的參數中,橫滾角?、俯仰角θ的均方根誤差較小,航偏角ψ的均方根誤差較大。目標車輛在水平路面行駛,因此引起的橫滾角?、俯仰角θ的變化量較小,導致均方根誤差較小;目標車輛在交叉口轉向,因此引起的航偏角ψ的變化量大,由式(7)可知,航偏角受多個因素影響,由于目標車輛車體表面并非完全垂直,使得每個因素估計時都存在一定誤差,導致均方根誤差較大。
4 結束語
本文針對復雜城市交叉口場景下激光雷達獲取運動車輛點云殘缺而導致位姿信息難以提取的問題,提出一種基于點法向量特征的動態剛性目標實時位姿估計方法,采用自適應聚類算法求解點法向量聚簇中心的數量,通過隨機采樣一致性算法對屬于同一聚類的點進行平面擬合,通過運動學方程完成目標的三維姿態角求解,采用均方根誤差來衡量不同方法獲得車輛位姿估計值與真值之間的誤差關系,結果表明,運動車輛進行直線與曲線運動時采用點法向量位姿估計效果均優于傳統基于迭代最近點的方法,具有較高的準確性,能克服點云殘缺性。由于本方法僅對動態剛性目標進行實時位姿估計,并未考慮運動狀態變化過程,后續應對動態目標狀態估計及預測方法展開深入研究。

