鋼梁橋豎向彈塑性地震反應分析的非線性位移系數法
尹 劍
(山西交通科學研究院集團有限公司,太原 030006)
實際震害、試驗研究和數值模擬均表明:豎向地震動及其作用效應可對橋梁結構形成嚴重不利影響。1995年的日本阪神地震中,大量橋墩發生剪切破壞[1]。隨后的試驗表明:上述剪切破壞主要由豎向地震作用引起的橋墩軸力變化導致[2]。根據相關計算結果:豎向地震動引起的橋墩軸力變化影響橋墩滯回性能,并會加劇橋墩塑性區的變形[3]。特別地,在近斷層豎向地震動影響下,橋墩軸力和橋梁體豎向撓度明顯增大[4]。例如,針對某實際橋梁結構的計算表明[5]:豎向地震作用可使其空心橋墩的軸力增加90%以上。
對于橋梁上部結構,豎向地震動的不利影響亦非常顯著。于向東等[6]分析了大跨簡支鋼桁梁橋-軌道系統的動力響應特征,結果顯示:豎向地震激勵可使桁架最大拉、壓軸力分別增大1.5倍和0.8倍;鄧子銘等[7]將軌道不平順作為鋼桁梁橋車橋系統的自激激勵源,將地震作為外部激勵,模擬了地震對車橋系統耦合振動的影響,其結果表明:豎向地震波對車橋系統的豎向振動、脫軌系數、輪重減載率和車體豎向加速度影響顯著。KUNNATH et al[8]的計算表明:豎向地震動使得橋梁主梁跨中及負彎矩區的內力需求大幅增大,GULERCE et al[9]的計算結果證實了上述結論。
現階段,精確計算豎向地震作用下橋梁結構的非線性地震反應,需采用增量動力分析(incremental dynamic analysis,IDA)方法[10]或云分析(cloud analysis,CA)方法[11]。由于上述方法涉及大量非線性時程分析計算,且需要合理遴選地震波并對計算結果進行統計分析,故難以普遍應用于量大面廣的工程實踐。相比之下,靜力非線性分析方法(Pushover Analysis)以設計反應譜為基準,分析耗時短,計算結果清晰直觀,更易且更宜被工程師掌握使用[12]。李宇等[13]考慮高階振型影響,統計了與我國《鐵路工程抗震設計規范》相應的強度折減系數譜和彈塑性需求譜,從而建立了可考慮高階振型影響、適用于鐵路高墩橋的能力譜方法。柳春光等[14]將基于能量平衡的Pushover方法應用于橋梁橋墩的抗震性能評估,其計算結果表明:該方法所得結果與非線性時程分析結果吻合良好。現階段,除用于求解橋梁結構地震反應外,Pushover方法亦被用于分析橋梁結構的非線性承載行為。例如,李曉莉等[15]利用Pushover分析模擬橋臺在主梁撞擊下的水平力-位移關系,簡濤等[16]則通過Pushover分析確定橋梁墩柱的損傷指標。
囿于對結構水平向非線性受力-變形關系(Pushover曲線)的依賴,Pushover方法難以應用于承受豎向地震作用的梁橋結構(尤其是上部結構)。近年來,XIANG et al[17]利用結構的整體剛度參數指標建立了拓展的模態Pushover分析方法,有效克服了上述問題,使得Pushover方法被拓展應用于拱[17]、網殼[18]和索網[19-20]等結構的非線性地震反應分析。基于該方法分析梁橋結構的豎向振動特性和豎向非線性地震反應,成為評估此類結構豎向抗震性能的有力手段之一。采用上述方法,將梁橋豎向非線性能力曲線與合理的豎向地震需求譜相結合,可快速確定梁橋在豎向地震作用下的目標位移。
在上述背景下,本文以鋼梁橋作為切入點,首先分析此類結構在豎向地震作用下的非線性振動特點,建立適用于描述此類結構豎向振動的非線性簡化模型;基于大量實際近場豎向強震記錄,以豎向非線性位移系數作為地震需求指標,計算鋼梁橋的豎向非線性位移需求,據此建立此類結構的豎向非線性位移系數譜(需求譜);隨后,為驗證本文所建立的豎向非線性反應譜的適用性和準確性,給出一個鋼桁架梁橋豎向非線性地震反應分析算例。本文所建立的豎向非線性位移系數譜方法,計算耗時短,所得結果準確度高,便于實際工程應用。
1 鋼梁橋豎向地震反應分析簡化模型
與水平地震作用下的結構振動反應不同,大跨度鋼梁橋上部結構在豎向地震作用下的非線性振動呈現出明顯的非對稱性。該非對稱性主要是由預加在結構上的重力作用導致。承受豎向地震作用之前,鋼梁橋結構處于重力平衡狀態,豎向地震激勵施加于鋼梁橋后,其上部結構以重力平衡狀態為初始平衡位置開始振動。在豎向地震作用向下,地震作用效應與重力作用效應疊加,鋼梁橋傾向于進入彈塑性狀態;而當豎向地震作用向上時,地震作用與重力作用效應部分相抵,鋼梁橋傾向于保持彈性。本質上,鋼梁橋上的預加重力作用使得其在重力平衡位置“之上”和“之下”呈現出不同的等效屈服點和等效承載力,從而使得其豎向振動體現出非對稱特點。
事實上,由預加重力作用導致的大跨度結構豎向地震反應的非對稱性,已在建筑結構領域得到重視。XIANG et al[21-22]建立了大跨度鋼屋蓋和鋼樓蓋結構豎向振動的非對稱滯回模型,并計算了此類模型的非線性位移需求譜。本質上,大跨度鋼梁橋的豎向非線性地震反應與大型鋼屋(樓)蓋結構類似。例如,對于從重力平衡狀態向上運動時的振動位形,豎向地震動偽加速度值需達到1.0g,方可克服鋼梁橋上部結構的自重作用,使結構達到“重力作用卸除”狀態。相對地,對于重力平衡位置之下的振動位形,偽加速度值為1.0g的豎向地震動與重力作用疊加,將使得鋼梁橋承受約2.0g的等效重力荷載。當鋼梁橋上運行有重型移動荷載時,較大的豎向地震作用極易使得鋼梁橋上部結構在向下振動時進入彈塑性階段;而由于重力作用的有利影響,結構在向上振動時,一般仍處于彈性階段。
基于以上論述,可建立鋼梁橋結構在豎向地震作用下的非線性滯回模型,如圖1所示。圖中,鋼梁橋結構在重力平衡位置“之下”的振動反應為彈塑性,“之上”的振動反應為彈性,總體上,該體系呈現出明顯的非對稱滯回特點。由于本文的討論限于鋼梁橋結構,故假定結構的彈塑性滯回曲線不存在退化現象,在重力平衡位置“之下”的振動位形,結構的非線性等效荷載(Feq)-等效位移(deq)的關系為雙折線型。
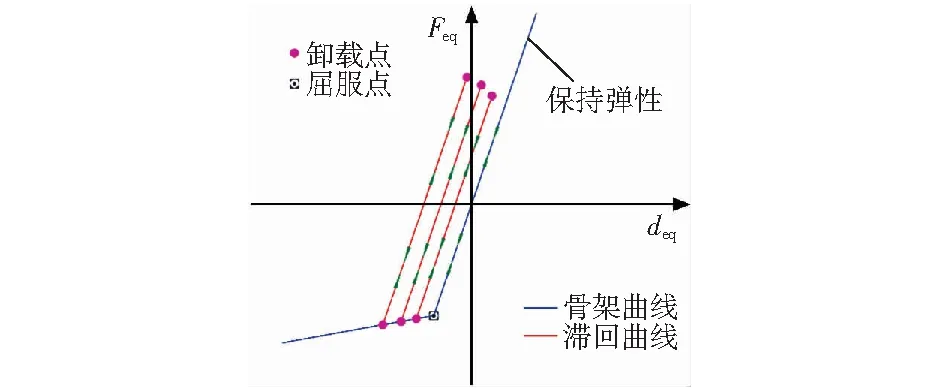
圖1 鋼梁橋豎向振動簡化滯回模型Fig.1 Simplified hysteresis model for the vertical vibration of steel beam bridge
2 近場豎向地震動
基于圖1所示的鋼梁橋豎向振動簡化滯回模型,可結合實際豎向強震記錄,計算鋼梁橋的豎向非線性地震位移需求,進而對計算結果進行統計分析,提出相應的非線性位移系數譜模型。本文選取53條豎向強震記錄作為鋼梁橋結構豎向非線性位移需求的計算依據,所選取的所有豎向強震記錄均為近斷層地震地面運動時的豎向分量,記錄臺站距離震源的水平距離小于30 km.各豎向地震動記錄的峰值豎向地面加速度(PGA)均大于0.14g,其中,最大豎向PGA值達0.82g.上述地震動數據源自日本NIED強震記錄網站K-NET,限于篇幅,地震記錄的詳細信息不再列出。圖2(a)給出了各豎向地震記錄的震源-記錄臺站相對位置,即震中距、震源深度數據;圖2(b)給出了各豎向強震記錄的偽加速度反應譜,各反應譜阻尼比均為0.02.
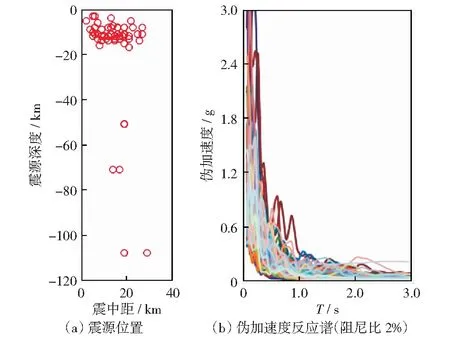
圖2 豎向強震記錄Fig.2 Strong vertical seismic records
3 豎向非線性位移系數譜
豎向地震作用下,鋼梁橋的豎向非線性位移需求與其屈服強度、屈服后剛度、豎向彈性自振周期T有關。利用拓展的模態推覆分析方法[17],針對鋼梁橋的豎向振型,可將多自由度的鋼梁橋計算模型轉化為等效單自由度非線性體系模型,進一步地,可計算鋼梁橋在豎向地震作用下的非線性反應。
3.1 計算流程及主要結果
本文以豎向非線性位移系數(inelastic displacement ratio,IDR)作為衡量鋼梁橋豎向地震需求的指標,基于IDR-T格式的豎向非線性位移系數譜建立鋼梁橋的豎向地震需求譜。為在計算鋼梁橋豎向IDR值的過程中考慮結構豎向屈服強度和豎向屈服后剛度的影響,需定義一系列結構關鍵參數。本文所考慮的鋼梁橋豎向非線性滯回模型的關鍵參數,包括彈性剛度ke、屈服后剛度kpy、彈性位移及力需求de及Fe、彈塑性位移及力需求dp及Fp、屈服強度及屈服位移Fy及dy,豎向強度折減系數R=Fy/Fe=dy/de.各參數定義如圖3所示。圖中各變量均為鋼梁橋等效單自由度體系參數。
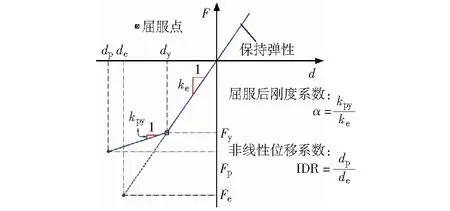
圖3 鋼梁橋豎向滯回模型關鍵參數Fig.3 Key parameters of the vertical hysteresis model for steel beam bridges
基于所定義的參數,制定以下(1)、(2)兩步IDR計算步驟:
1) 基于圖1給出的非線性滯回模型,選定結構豎向強度折減系數R、屈服后剛度系數α和彈性豎向自振周期T,計算體系在53條豎向強震記錄作用下的彈性位移需求de和彈塑性位移需求dp,并依據式(1)計算體系豎向IDR值:
(1)
2) 調整體系R、α和T值,計算參數變動后的體系豎向位移需求de和dp,并據此進一步計算相應的IDR值。
本文共考慮6種豎向強度折減系數值,分別為R=0.3,0.4,0.5,0.6,0.7,0.8;6種豎向屈服后剛度系數值,分別為α=0.1,0.2,0.3,0.4,0.5,0.6;所考慮的體系彈性自振周期T的變化范圍為T=0.05~2.75 s,周期間隔0.05 s,共55個值。結合53條地震動記錄,本文共計算了6×6×55×53=104 940個鋼梁橋豎向IDR值。
上述非線性位移需求均基于Newmark-β積分法求得。需要說明的是:由于鋼梁橋豎向非線性滯回模型的非對稱特征,在運用Newmark-β法進行非線性時程積分計算時,需對該算法中“確定系統當前狀態”的步驟進行修正(相關列式見本文附錄),使得所求出的體系位移反應和滯回特征與實際狀況相符。上述Newmark-β積分算法在Matlab程序平臺實現,限于篇幅,算法程序及其驗證算例從略。
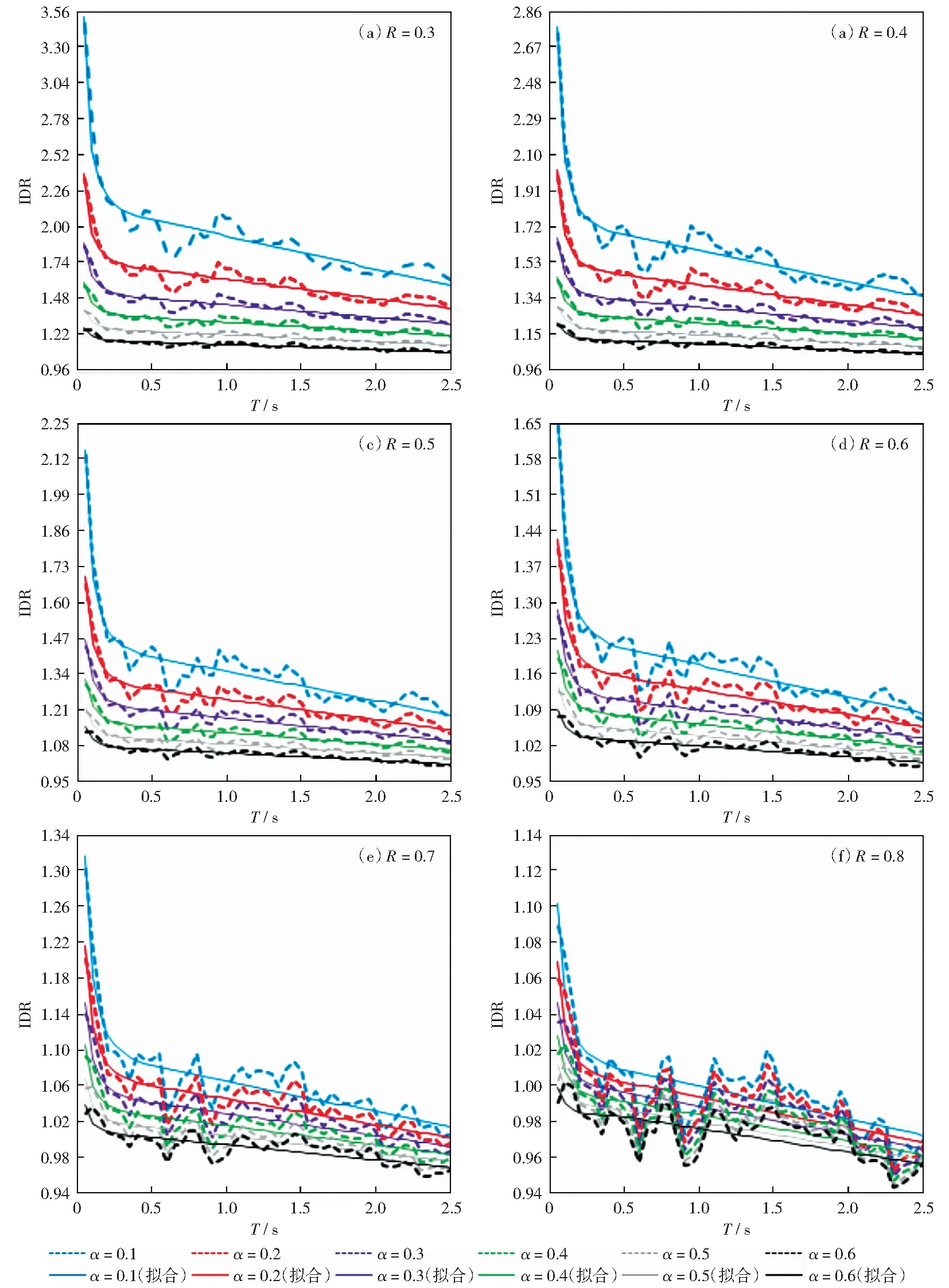
為綜合考量R和α對鋼梁橋豎向IDR值的影響,圖4和圖5給出了基于53條豎向強震記錄計算得到的豎向IDR-T譜的部分結果,包括對應于各單條地震動記錄的IDR-T譜(灰線)和均值IDR-T譜(紅線)。圖4列出了與α=0.1對應的6組豎向IDR譜,各子圖的R值從0.3增至0.8.顯然,R值越大,體系屈服強度相對于彈性強度需求越高,其對應的非線性位移需求就越低,相應地,IDR值隨R值增加而降低。圖5列出了與R=0.5對應的5組豎向IDR譜,各子圖的α值從0.2增至0.6.結合圖4(c)可見:α值越大,體系屈服后剛度越大,其非線性位移需求(IDR值)越低。
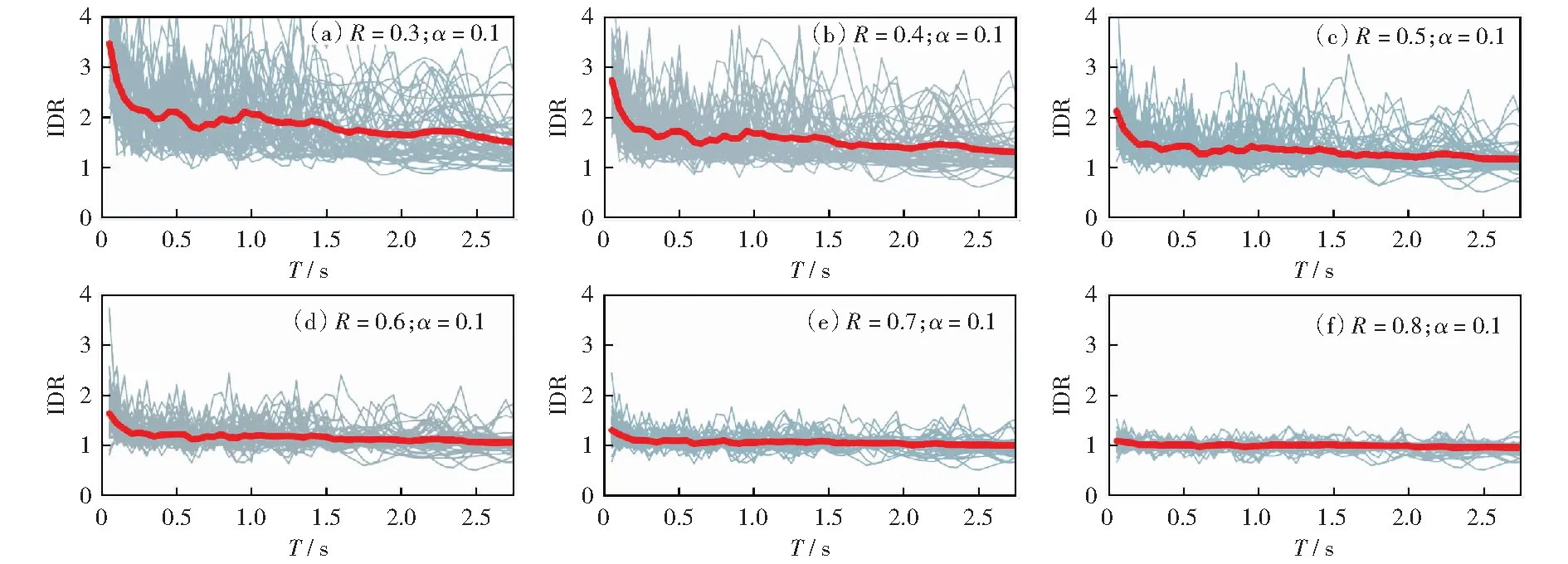
圖4 強度折減系數對鋼梁橋豎向IDR譜的影響(α=0.1)Fig.4 Effect of strength reduction factor on the vertical IDR spectra for steel beam bridges (α=0.1)
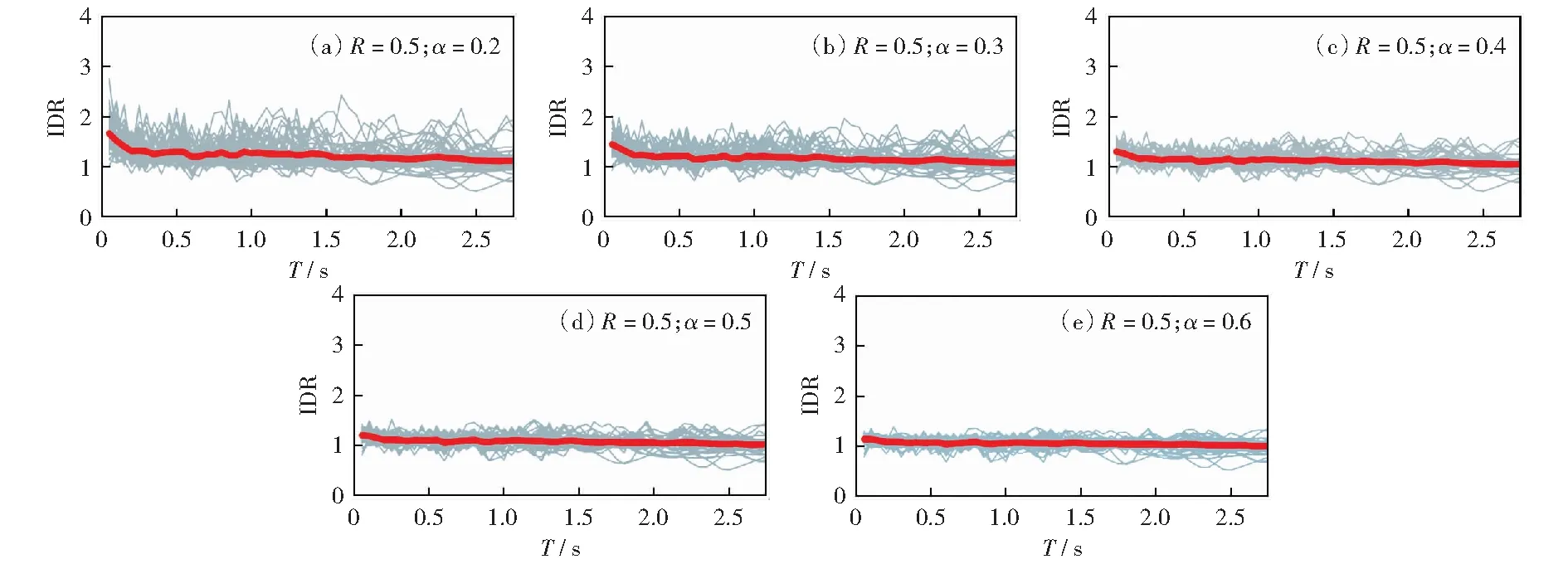
圖5 屈服后剛度系數對鋼梁橋豎向IDR譜的影響(R=0.5)Fig.5 Effect of post-yield stiffness ratio on the vertical IDR spectra for steel beam bridges (R=0.5)
3.2 豎向非線性位移系數譜公式
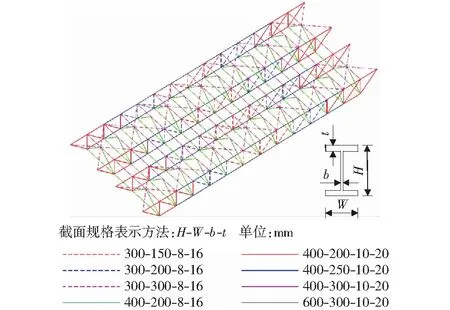
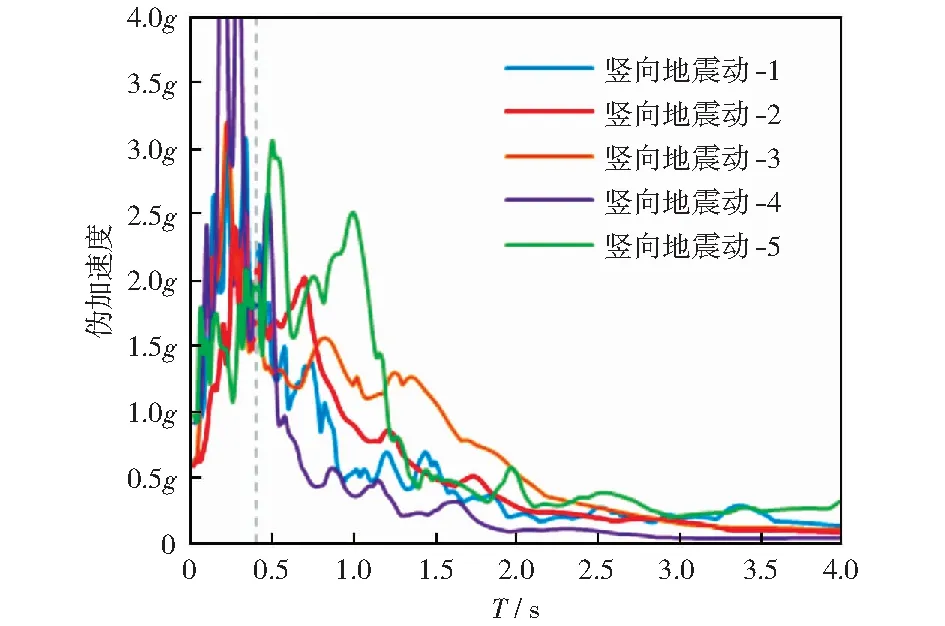
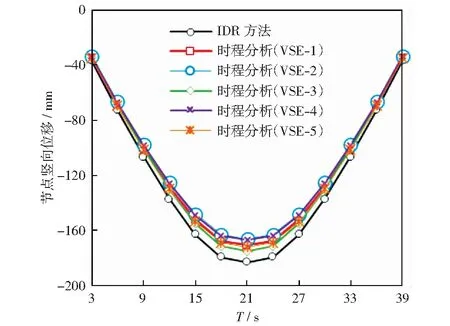
與6個R值和6個α值對應,本文共計算得到36組豎向IDR-T譜,各組譜線的均值可直接用于歸納鋼梁橋結構在豎向地震作用下的IDR譜表達式。根據計算結果,豎向IDR譜在短周期段(0 (2) 式中:A、B為短周期段(非線性段)擬合系數,C、D為中長周期段(線性段)擬合系數。與各組R和α相對應,各擬合系數值列于表1.實際應用中,鋼梁橋非線性單自由度模型的豎向R和α值一般與表中所列情況不等,此時可通過對表中所列數據線性插值得到公式(2)中的系數取值,從而確定IDR值。 表1 鋼梁橋豎向IDR公式擬合系數Table 1 Fitting coefficients of the vertical IDR formula for steel beam bridges 為證明公式(2)對鋼梁橋豎向IDR-T譜的擬合精度,圖6列出了基于實際地震動記錄計算得到的36組豎向IDR-T均值譜及其對應的擬合譜(由公式(2)給出)。由圖可見,公式(2)對實際IDR-T譜的擬合精度較高,實際IDR-T均值譜與其擬合譜的偏差較小。在短周期段和中長周期段,公式(2)分別較準確地還原了實際IDR-T均值譜的非線性和線性特征。 至此,可將拓展的模態推覆分析(Pushover)方法和本文給出的豎向IDR譜公式結合起來,估算鋼梁橋在豎向地震作用下的非線性反應,所得結果可直接用于指導鋼梁橋抗震設計和抗震性能評估。為便于應用,本節將上述分析方法的基本計算流程加以梳理: 1) 對鋼梁橋結構實施模態分析,依據質量參與系數,遴選其豎向主振型。一般情況下,鋼梁橋的豎向第1階振型為其豎向主振型,結構在豎向地震作用下的反應將由第1階振型主導。 2) 依據拓展的模態推覆分析方法[17],結合鋼梁橋豎向主振型,實施推覆分析。需要注意的是,推覆分析的起始位置應為梁橋重力平衡位置。鑒于鋼梁橋豎向振動的不對稱性,其非彈性地震反應均出現在重力平衡位置“之下”的振動位形上,故推覆分析應自重力平衡位置始,確定推覆荷載方向,對梁橋實施向下推覆加載分析,并依據所得數據建立鋼梁橋結構的豎向振動等效單自由度體系模型。 3) 依據所得非線性單自由度模型和設計反應譜,確定鋼梁橋豎向屈服后剛度系數α和強度折減系數R,結合其豎向主振型自振周期T,依據本文公式(2)計算其非線性位移系數需求(IDR值)。在此步驟中,一般需先預估結構峰值反應,以便裁出用于確定屈服后剛度系數的豎向推覆曲線的范圍。依據經典但粗糙的“等位移原理[23]”,可先假定結構峰值彈塑性位移反應與峰值彈性位移反應相等(dp≈de),在此假設下,截取豎向推覆分析曲線的相應范圍,即可據此確定結構的屈服后剛度系數。 4) 依據IDR值和公式(1),計算鋼梁橋等效單自由度體系非線性目標位移dp,依據豎向推覆分析結果,計算與dp對應的結構整體豎向地震反應。 圖6 鋼梁橋豎向IDR譜擬合公式精度示意Fig.6 Illustration of accuracy of fitting formula of the vertical IDR spectra for steel beam bridges 由于上述計算過程不涉及非線性時程分析,故效率很高。同時,上述過程步驟清晰,概念直觀,非常便于工程師運用。 為驗證本文所建立的豎向非線性位移系數法的計算精度和效率,并演示該方法分析流程,本節給出一個數值算例。 算例所用鋼梁橋為桁架梁橋,兩端簡支,由4榀縱向主桁架和13榀橫向支撐桁架構成,主桁架上弦設置面內橫向交叉支撐。梁橋跨度42 m,寬16 m.梁橋上附荷載由混凝土面板、路基面層、部分移動活載等構成。梁橋的幾何尺寸、平面布置及節點等效集中質量如圖7所示。梁橋由H型鋼拼裝構成,其構件布置如圖8所示。 圖8 鋼梁橋構件布置Fig.8 Member arrangement of steel beam bridge 鋼梁橋模型在ANSYS有限元平臺內建立,型鋼構件和節點集中質量分別采用beam189單元和mass21單元模擬。鋼材非線性滯回本構關系由文獻[24]中所標定的公式(4)模擬。結構阻尼采用Rayleigh阻尼模型模擬,各階振型阻尼比均設為0.02.在重力平衡狀態對結構進行自振特性分析,依據分析結果,鋼梁橋第1階振型的豎向質量參與系數達到84.66%,為豎向主振型。該振型周期為T1=0.40 s,其振型形態如圖9所示。 圖9 鋼梁橋豎向主振型Fig.9 Vertical dominant vibrating mode of the steel beam bridge 依據鋼梁橋主振型對應的荷載模式,采用文獻[17]建立的拓展模態推覆分析方法對鋼梁橋進行豎向靜力推覆分析,可建立結構主振型等效單自由度體系的等效荷載-位移關系,如圖10(a)所示。由圖可見,由于預加重力效應,當靜力推覆荷載方向向下時,鋼梁橋等效單自由度體系在deq≈-40 mm時即進入塑性階段,而當靜力推覆荷載方向向上時,結構等效單自由度體系在deq≈110 mm仍保持彈性。將圖10(a)所示等效單自由度體系的等效荷載-位移曲線雙折線化,可得該體系等效屈服位移deq,y=-40 mm.雙折線化荷載-位移曲線如圖10(b)所示,由圖中數據可求得等效單自由度體系屈服后的剛度系數α: (3) 圖10 鋼梁橋豎向推覆分析曲線Fig.10 Vertical pushover curve of steel beam bridge 選擇5條豎向強震記錄作為地震激勵。所選豎向地震波的偽加速度反應譜如圖11所示。需要說明的是:該5條地震波不在本文第2節所選的53條豎向近場地震記錄之中。分析中,對地震動實施了縮放。經縮放,各豎向地震動偽加速度反應譜對應T1=0.40 s的譜值為2.0g. 圖11 豎向地震動偽加速度反應譜(縮放后)Fig.11 Pseudo acceleration response spectra of vertical seismic records (amplified) 在T1=0.40 s處,縮放后的地震動輸入所對應的彈性位移需求為deq,e=79.4 mm,故鋼梁橋等效單自由度體系的豎向強度折減系數為: (4) 注意到T1=0.40 s<0.50 s,R=0.504,α=0.204,結合式(2),可計算得到與上述數據對應的鋼梁橋結構等效單自由度體系豎向IDR值: (5) 式中:A、B數值系通過對表1所列數值線性內插得到。基于IDR值和等效單自由度體系彈性位移需求,可求得其峰值非線性位移需求: deq,p=IDR·deq,e=1.286×79.4 mm=102.1 mm . (6) 依據等效單自由度體系峰值位移需求deq,p,可進一步得出鋼梁橋結構整體峰值位移反應。 為驗證豎向非線性位移系數法的計算精度,本節將豎向IDR譜分析結果與非線性時程分析結果進行對比。圖12繪出了采用豎向非線性位移系數法和非線性時程分析法計算得到的鋼梁橋上弦節點峰值豎向位移。由圖可見:基于IDR方法計算得到的鋼梁橋峰值豎向位移模式與非線性時程分析方法一致,數值上,IDR方法計算結果稍高于非線性時程分析結果,但二者偏差很小。以結構跨中節點豎向位移為例:對應豎向地震激勵VSE-1~VSE-5,基于豎向IDR譜得到的位移峰值相對于時程分析結果的誤差分別為:7.30%,10.15%,4.49%,9.62%和6.36%. 圖12 采用IDR法與非線性時程分析法得到的豎向位移反應峰值Fig.12 Peak vertical displacement responses given by the IDR method and the nonlinear RHA approach 與節點位移反應對應,關于鋼桁梁的屈服構件數量及分布位置,IDR方法的計算結果也與非線性時程分析結果一致,限于篇幅,不再詳列。 1) 在豎向地震作用下,鋼梁橋自重力平衡位置向下振動時,地震作用效應與重力作用效應疊加,鋼梁橋傾向于進入彈塑性階段;自重力平衡位置向上振動時,地震作用與重力作用效應部分相抵,鋼梁橋傾向于保持彈性。據此,建立了鋼梁橋豎向振動的非對稱滯回模型。 2) 基于所建立的豎向非對稱滯回模型,采用53條近場豎向強震記錄(大震)和自編非線性動力反應分析程序,計算了鋼梁橋在豎向地震作用下的彈塑性位移需求。結果表明:鋼梁橋等效豎向屈服強度越高,或其屈服后剛度系數越高,鋼梁橋的彈塑性位移需求越低,且該需求的離散性越小。 3) 基于計算結果,擬合得到了鋼梁橋在豎向地震作用下的彈塑性位移系數公式。 4) 給出了結合豎向靜力推覆分析和豎向非線性位移系數公式的鋼梁橋彈塑性地震反應分析流程,可據此快速求得鋼梁橋在豎向地震動(大震)作用下的彈塑性地震反應。 5) 采用所建立的豎向非線性位移系數法計算一個鋼桁架梁橋在豎向地震作用下的彈塑性反應,所得結果與時程分析結果吻合良好。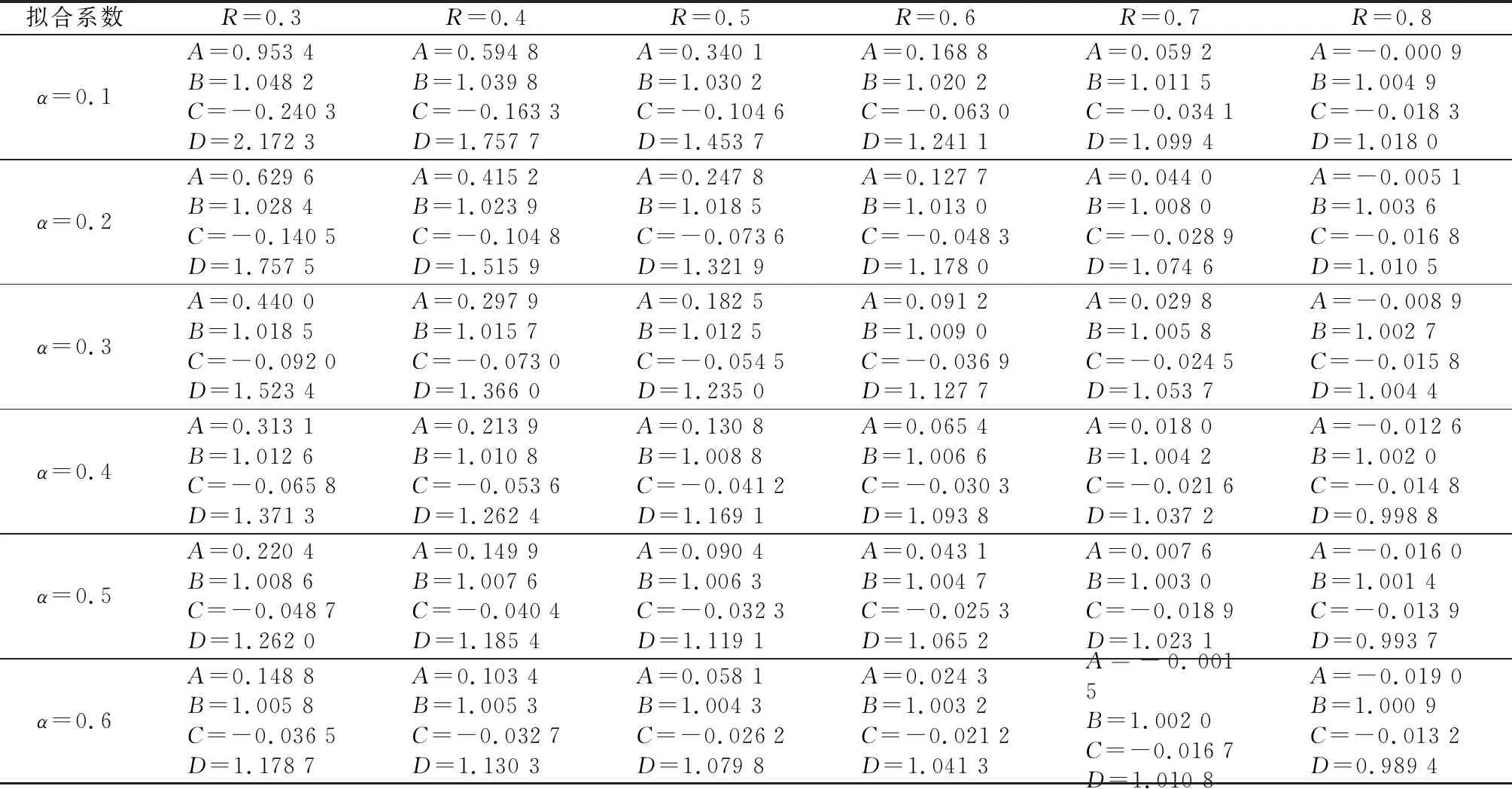
4 基于IDR-T的鋼梁橋豎向地震反應分析
5 數值算例
5.1 結構模型

5.2 豎向推覆分析

5.3 豎向推覆分析
5.4 計算結果對比
6 結論

