再探橢圓的一個定值命題的推廣*

(安徽省滁州中學 239000)

本文通過對橢圓的一個定值命題的推廣過程進行反思，揭示這一定值命題的幾何意義，繼而給出能夠推廣的原因：關于原點對稱的點，其極線關于原點對稱.文[1]對橢圓中的一個與焦點弦有關的定值命題進行了探究.該命題為：

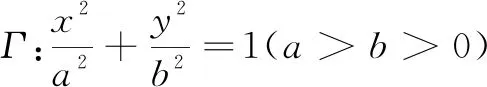
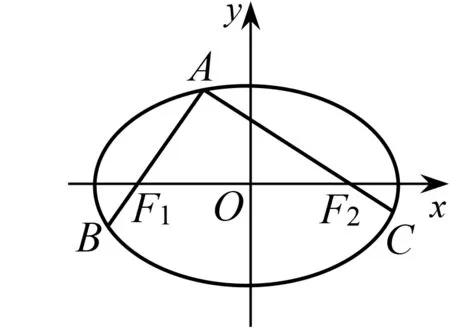
圖1

文[1]最終通過分析解析幾何的坐標法證明思路，獲得一般化探究的路徑，從而完成對這一命題的推廣.為了從幾何角度進一步解釋文[1]為什么能夠對命題1進行推廣，需要給出一個能夠揭示命題1幾何意義的證明，即：

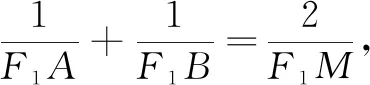
圖2

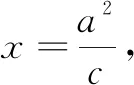
本文討論過程中涉及的線段均指有向線段.

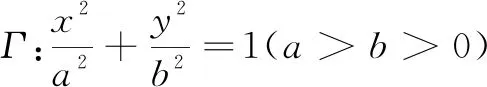
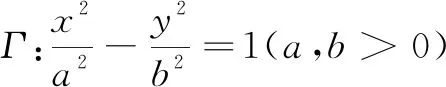
先以命題2為例，說明能夠推廣的原因，然后以此為基礎，指出能夠推廣為命題3的原因.

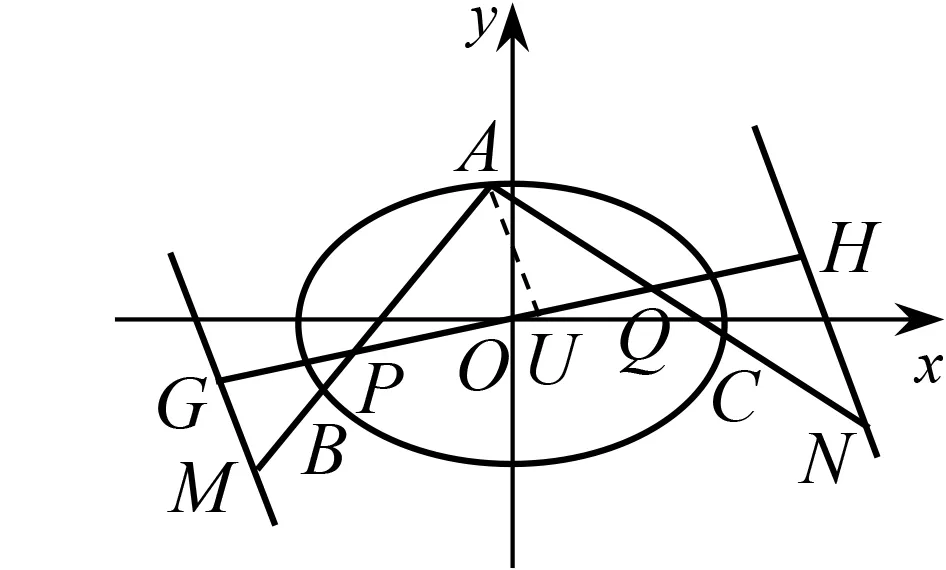
圖3

證明設點P，Q的極線與直線PQ分別交于點G，H，直線AB交點P的極線于點M，直線AC交點Q的極線于點N，過點A作極線的平行線交直線PQ于點U．

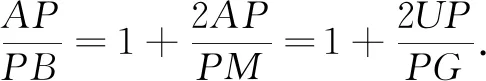
文[1]提出將點A分裂為兩點A1，A2，得出一個更為一般性的命題.通過對命題1能夠推廣為命題2和命題3的原因的分析，接下來給出這一命題的證明，并且給出其推廣命題.觀察文[1]提出的最后一個命題：

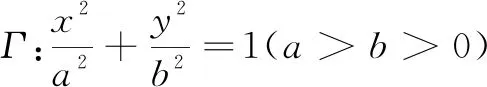
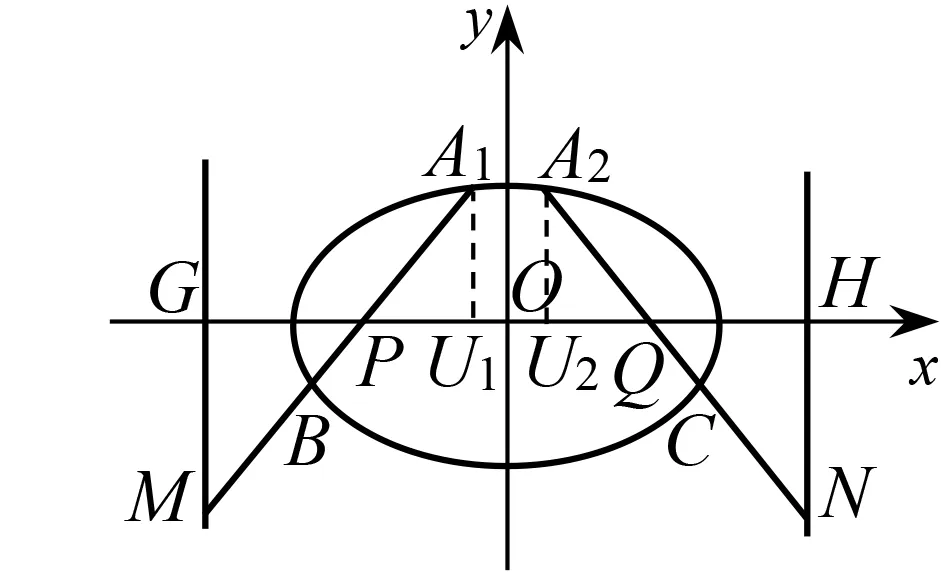
圖4

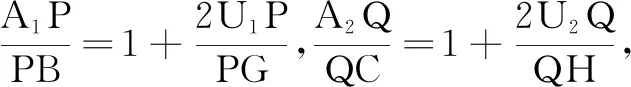
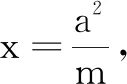
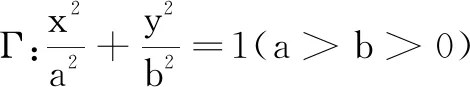
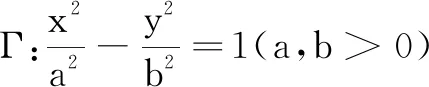
獲得圓錐曲線的一般性命題并非是圓錐曲線問題的探究終點，更為重要的是探討圓錐曲線命題的幾何意義，從而獲得對命題的透徹理解.通篇考慮本文對這一定值結論的反思歷程，最為關鍵的一步是獲得能夠揭示命題1的幾何意義的證明，正是從文[1]提出的推廣命題中，看出定值的代數式的幾何意義，才得出一個關鍵判斷：橢圓的這一定值命題極有可能是由焦點、準線的關系(極點極線)生成的，最后形成本文的命題1的新證.