對解析幾何中定點定值問題的一些思考

宗 蕾 (江蘇省常熟市中學 215500)

解析幾何是高考必考的內容，它通過研究空間與數量的關系，可以培養學生的直觀想象、數學抽象、邏輯推理等素養．解析幾何中曲線的性質常常以一些定點及定值問題的形式出現，比如證明動直線經過定點或計算某些量(如向量的數量積)是定值，在邏輯上體現了“動”與“定”的辯證關系，成為高考的熱點問題．同時，由于這些問題一般計算量大、字母較多、方法靈活多樣，也成為學生學習的難點．探索這類問題的多種解題方法，有助于提高學生解決問題的能力，提升學生的數學學科素養．

1 科學預設方法，提升運算效率

解析幾何中“動”與“定”的辯證關系決定了解題的方法具有多樣性.教師在課堂上要引導學生根據問題的條件和問題本身，設計好整個計算的方法，然后通過比較分析各方法的繁簡，選擇最優的方案進行求解，這樣往往會事半功倍．

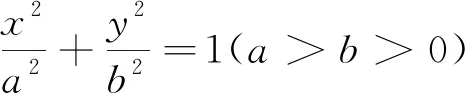
(1)求橢圓的方程；

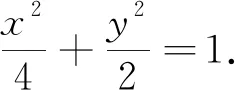
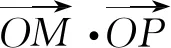
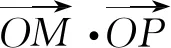
通過比較發現，方法1是利用斜率k為參數，需要求兩個點的坐標，計算量比較大，過程比較復雜；方法2利用點M的縱坐標為參數，將一次的直線與兩次的橢圓方程聯立，只計算了一次，計算量小了很多；而方法3是兩個一次的直線方程聯立，計算量最小、效率最高．因此，方法3是本題最好的方法．

2 夯實常規技能，避免思維固化

解析幾何的教學、特別是定點定值問題的教學，要注重常規經典方法的滲透，該“死算”的時候千萬不能取巧走捷徑．但是，事物都有其普遍性和特殊性，教師也要避免學生出現解法固化、思維固化的情形，即在過分強化某種解法后，學生可能出現不管什么問題都采用這種解法的情況，想利用一種解法“打遍天下”．這種情況下，一旦出現跟常見的情形不同的陌生情形，學生思維容易受阻，導致解題不順暢．這應是我們在解析幾何相關教學中盡量避免的情況．

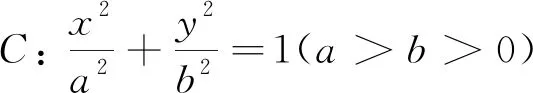
(1)求橢圓C的標準方程．

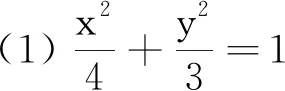
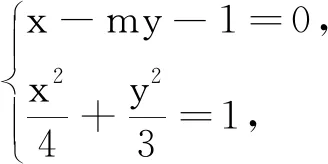
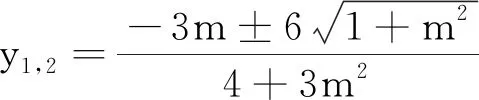
3 利用特殊設定，打開思維閘門

從特殊到一般是重要的數學思維方式．解析幾何的定點定值問題，在很多時候可以借助特殊情形來猜測答案．比如在證明動直線過定點的時候，可以將動直線中的參數取兩個特殊值，然后聯立起來，解出的交點就是所求的定點；再比如求定值的問題中，可將直線或者圓特殊化，就能經過簡單的計算得出答案．但是要注意，這樣僅僅代表了一種特殊的情形，依然需要對此給出證明．

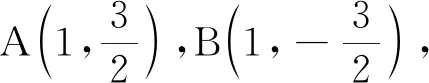
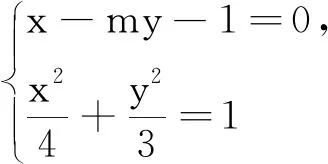
上面的解法就是采用了由特殊情形到一般情形的方法，計算量較小、易于掌握．

解析幾何的定點定值問題作為高考的中檔題，需要一定的計算能力．教師應該做到：(1)在課堂上給學生足夠的時間去計算，避免學生“看題”代替“算題”，避免計算時淺嘗輒止．課后作業的布置盡量少而精，以便給學生充裕的時間去獨立計算．(2)加強過程評價，鼓勵學生獨立計算的精神，并及時糾正學生計算過程、方法的錯誤，對計算的關鍵點適當地剖析．(3)增加對作業中計算的評語，鼓勵學生敢于計算、克服畏難畏繁的心理，增強學生“頑強計算”的意志和品格．