結合數學思想 培養核心素養
——以解三角形中方程思想運用為例

王弟成 (江蘇省蘇州實驗中學 215011)

數學思想方法是對數學知識內容及其所使用的方法的本質認識，數學思想也是數學知識到數學素養的橋梁，掌握了它就能駕馭知識，尋找到解決問題的方法．教學實踐中我們發現，在落實“四基”過程中抓住“基本思想”教學，對數學思想方法進行有效的滲透、揭示、運用，不僅能促進學生“四能”提高，也是落實并提升學生核心素養的有效抓手．本文以幾道三角題求解為例，談談自己的理解．

1 問題呈現

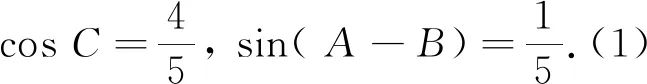
這道三角綜合題條件簡潔明了，主要涉及兩角和與差的三角函數．要求證的是兩角之間的正切關系，并在給定一邊長的條件下求該邊上的高．教材上有類似問題，應該說此題難度并不大，但在實際教學中發現，多數學生處理第(1)問的證明時問題不大，而對第(2)問卻束手無策，不知道從方程角度看問題，不能自覺運用方程思想整體把握問題．有的學生雖能列出關于邊的方程，卻不能結合目標對方程結構特點深入分析，導致列出了方程(組)卻不會解．也有學生雖然能做出來，但說不出所以然，不能從思想方法角度理解解法，解出了題卻無助于解題能力提高．

2 解法探究

2.1 利用方程思想整體把握問題

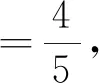
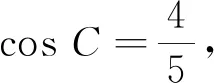
2.2 分析特點解方程

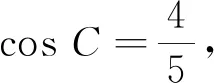
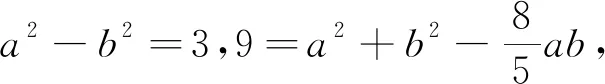
2.3 改變目標創新思路

若重新審視目標，換個角度思考，求面積關鍵是求ab的值，而求ab的值并不一定要分別把a與b的值都求出來，首先應考慮整體求解，看是否能整體求出ab的值．

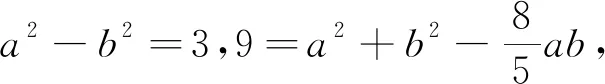
兩條思路都很清楚，都是學生會選的思路，都體現了方程思想指導下的思路探尋，但選擇邊的困難主要在于解方程．目標一變，好法顯現，解法3中立足ab整體思考，則顯得輕松得多，因此認識越深刻，解法越簡捷．

2.4 數形結合變換思路

從上面分析知△ABC是銳角三角形，故可結合平面幾何知識解決．

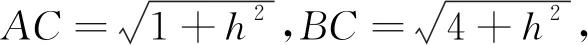
上述方法之所以能輕松解決問題，主要是利用條件結合平面幾何知識，構建了關于h的一元方程，而解決一元方程相對簡單多了．

3 在解題教學中運用方程思想提高學生學科素養

方程思想應用廣泛，中學數學中很多問題都可以運用方程思想整體把握，尋求思路，解決問題．教學中發現，學生會列方程解決問題，但沒有形成意識，不會從方程角度看問題，沒有形成素養．這就需要教師主動抓住機會滲透、揭示、運用思想方法，用思想方法指導概念的獲得和解題思路的形成，發揮思想方法這一有力武器的作用．同時，讓學生感受到思想方法不是空洞的，而是實實在在存在的，能指導我們高效思維．三角公式和解三角形中正、余弦定理本質上都是方程模型，正余弦定理的運用充分體現了方程思想．下面再以幾個例子加以說明．

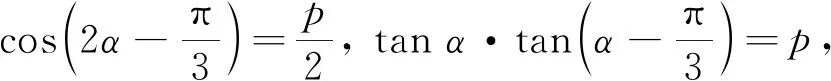
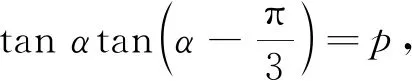
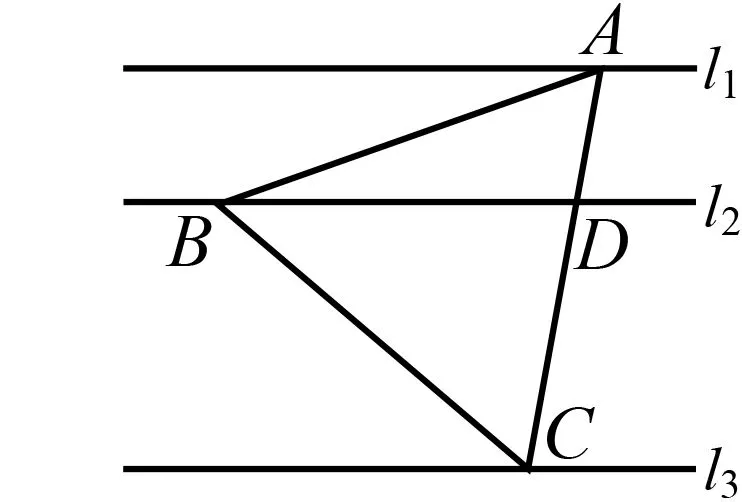
圖1

例2如圖1，l1，l2，l3是同一平面內的三條平行直線，l1與l2間的距離是1，l2與l3間的距離是2，正三角形ABC的三個頂點分別在l1，l2，l3上，則△ABC的邊長是( )．

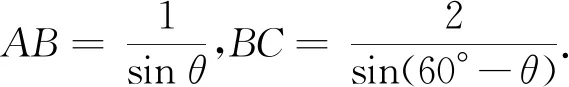
此題乍看無從入手，仔細分析后發現，立足三角形的邊和角，分別在兩個不同的、有聯系的三角形中建立含有邊和角的方程，兩個方程兩個未知數，解之即可．思路直接，目標明確，不需過多的思考，是解決此類問題的通性通法和程序化思維．把握這一點，就能找到解決三角問題的切入點．

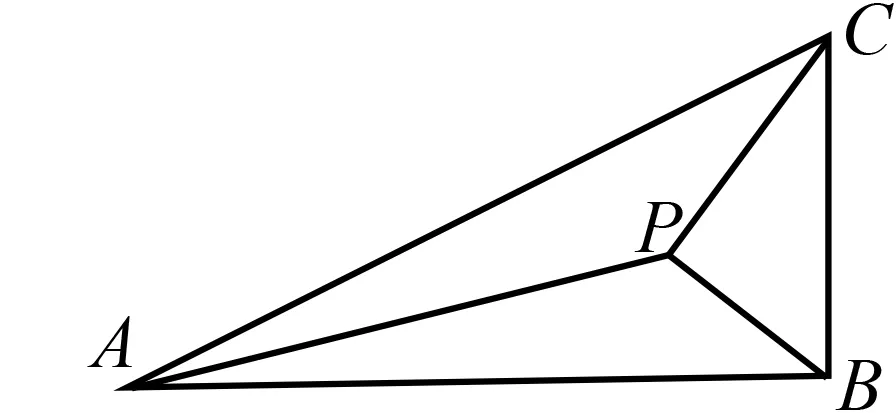
圖2

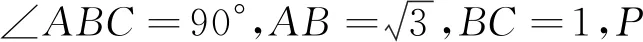
分析(1)根據已知條件直接使用余弦定理即可求解．

(2)從所求∠PBA出發，只要能建立關于∠PBA的方程即可，首先思考的是用∠PBA表示相關量．顯然題中其他的邊和角都可以用角∠PBA表示，如PC=cos∠PBA，PB= sin∠PBA，∠PAB=30°-∠PBA．

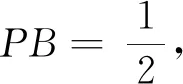
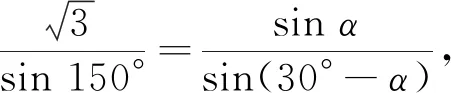
上述問題的求解過程中對問題的整體把握、對本質的深刻認識、對已知條件的合理使用、對解題方法的選擇、對解方程困難的突破、對算法的恰當選擇，都是在方程思想引領下完成的．在解題過程中，學生的“四能”得到培養，數學抽象、邏輯推理、數學運算等核心素養都得到提升,教學需要這樣的過程．