混沌頻率電場激勵乳化油液滴動力學仿真與響應

龔海峰， 廖治祥， 彭 燁， 邱 值， 余 保， 張賢明， 柳云騏

(1.重慶工商大學 廢油資源化技術與裝備教育部工程研究中心，重慶 400067；2.重慶工商大學 制造裝備機構設計與控制重慶市重點實驗室，重慶 400067；3.中國石油大學(華東) 重質油國家重點實驗室，山東 青島 266580)

近年來，新興發展的脈沖電場破乳法以其結構簡單、破乳速率快、工作能耗低等優點，在油-水分離領域得到了廣泛的應用[1-2]。Eow等[3-4]認為運用恰當的脈沖電場頻率能夠提高油液破乳脫水效率。Peng等[5]研究表明，脈沖電場能高效破乳的主要原因是，油中液滴在特定的脈沖頻率范圍內會發生劇烈伸縮變形的諧波共振，從而增大了相鄰液滴碰撞幾率，并減弱了液滴界面膜機械強度，致使聚結破乳得到有效強化。

然而，乳化油系統中的液滴粒徑分布跨度大，有微米級小液滴，也有毫米級大液滴，從而導致液滴諧波共振頻率的不統一和不確定。目前常用的恒定頻率或復合雙頻脈沖電場無法覆蓋乳化油中所有液滴的共振頻率，削弱了破乳效果。Peng等[6]嘗試手動調節的方式改變脈沖電場頻率，以應對液滴粒徑的不確定變化，但是手動調節電場頻率只能覆蓋油中部分液滴的諧振頻率，且操作性差。景微娜等[7]通過研究指出混沌電場破乳是未來電脫水技術發展的方向，并首次將混沌信號引入原油電脫水的研究，提供了各種脈沖混沌信號的獲取方法，基于線性振動理論建立了液滴變形動態模型，通過仿真獲得了在高壓脈沖電場脈沖低電平混沌、脈沖寬度混沌和脈沖幅值混沌下液滴的工作狀態，為混沌脈沖電場脫水的研究提供了啟發和指導。然而，該研究未充分考慮液滴振動變形的非線性及其混沌振動響應特性，存在一定的局限性。通過文獻[8]發現，由頻率混沌序列脈沖生成的高壓電場，頻率跨度極大，完全能夠覆蓋油中液滴的諧振頻率。于是筆者提出運用定幅值、等脈寬、頻率混沌的高壓脈沖電場實現油中液滴的高效聚結，將著重從非線性動力學的角度，利用數值仿真考察油中液滴在混沌頻率電場激勵下的動力學行為，探究其變形規律及響應特征，為建立高效實用的脈沖電場破乳新方法奠定基礎。

1 乳化液滴混沌電場振動動力學模型

1.1 混沌頻率脈沖電場

Sushchik等[9-10]提出了一種混沌位置調制的方法，為構建等幅值、等脈寬、頻率混沌的高壓脈沖電場提供了思路。通過混沌位置調制將混沌序列引入電場的脈沖間隔，使其占空比混沌，從而實現頻率混沌。筆者采用Logistic滿映射[11]構造一維混沌序列，再將該序列映射到脈沖電場的低電平時段，通過DSP控制器編程模擬映射后的混沌信號，控制脈沖開關的通斷實現混沌頻率脈沖電場的發生。其混沌頻率脈沖電場的發生電路等效模型及信號波形圖如圖1所示。

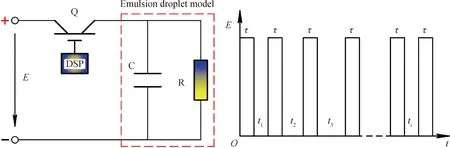
Q—Q-switching; C—Capacitance; R—Resistance; DSP—Digital signal processing圖1 混沌頻率脈沖電場發生電路及信號波形圖Fig.1 Electric field generating circuit and signal waveform of chaotic frequency pulse

由圖1可知，所有脈沖寬度為τ，幅值為E，使脈沖間隔tn在[Tl,Tu]內混沌,其中Tl為下限,Tu為上限。則通過調制映射后的脈沖間隔為

(1)

混沌頻率脈沖電場可表示為

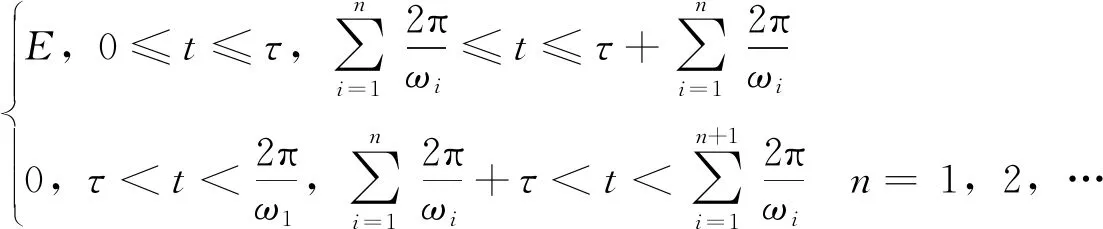
(2)

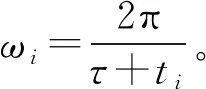
1.2 乳化液滴振動動力學模型

油中液滴在混沌頻率脈沖電場激勵下的變形振動會受到4個力的作用影響：一是液滴由自身質量產生的慣性力Fi；二是黏性油液對液滴變形產生的阻力Fr；三是由油-水界面張力產生的回復力Fh；四是混沌脈沖電場激勵液滴振動變形的電場激勵力Fe。則液滴在混沌電場激勵下的變形振動過程中受力平衡方程[12]如式(3)所示。

Fi+Fr+Fh=Fe

(3)

設油中某液滴在靜止狀態下呈半徑為R的圓球形，在混沌頻率脈沖電場作用下發生伸縮振動，液滴始終呈長球形，其體積與幾何中心保持不變。以液滴右半球為研究對象，在振動的某一瞬時，其長半軸為a，短半軸為b，將笛卡爾坐標系的坐標原點O建立在液滴的幾何中心上，x軸方向與電場方向平行，y軸方向垂直于電場方向向上，z軸方向垂直于電場方向向外，其受力變形如圖2所示。

圖2 油中液滴右半球的受力變形示意圖Fig.2 Stress deformation diagram of righthemisphere of droplet in oil

在該瞬時條件下，液滴半軸伸長量為δx=a-R，則液滴所受的慣性力Fi[13]如式(4)所示。

(4)

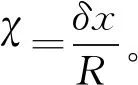
黏性油液對液滴振動變形的阻力Fr[14]如式(5)所示。

(5)

油-水界面膜的振動變形回復力Fh[7]如式(6)所示。

(6)

脈沖電場策動液滴振動變形的電場激勵力Fe[15]為

(7)

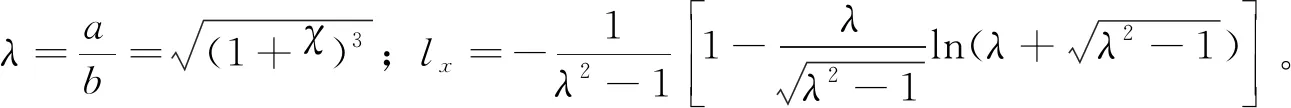
聯立式(2)～式(7)，可得油中液滴在混沌頻率脈沖電場中的動力學模型表達式為

(8)

式中：c(t)=

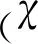
2 仿真輸出與方法

2.1 Simulink數學模型

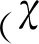
2.2 初始條件

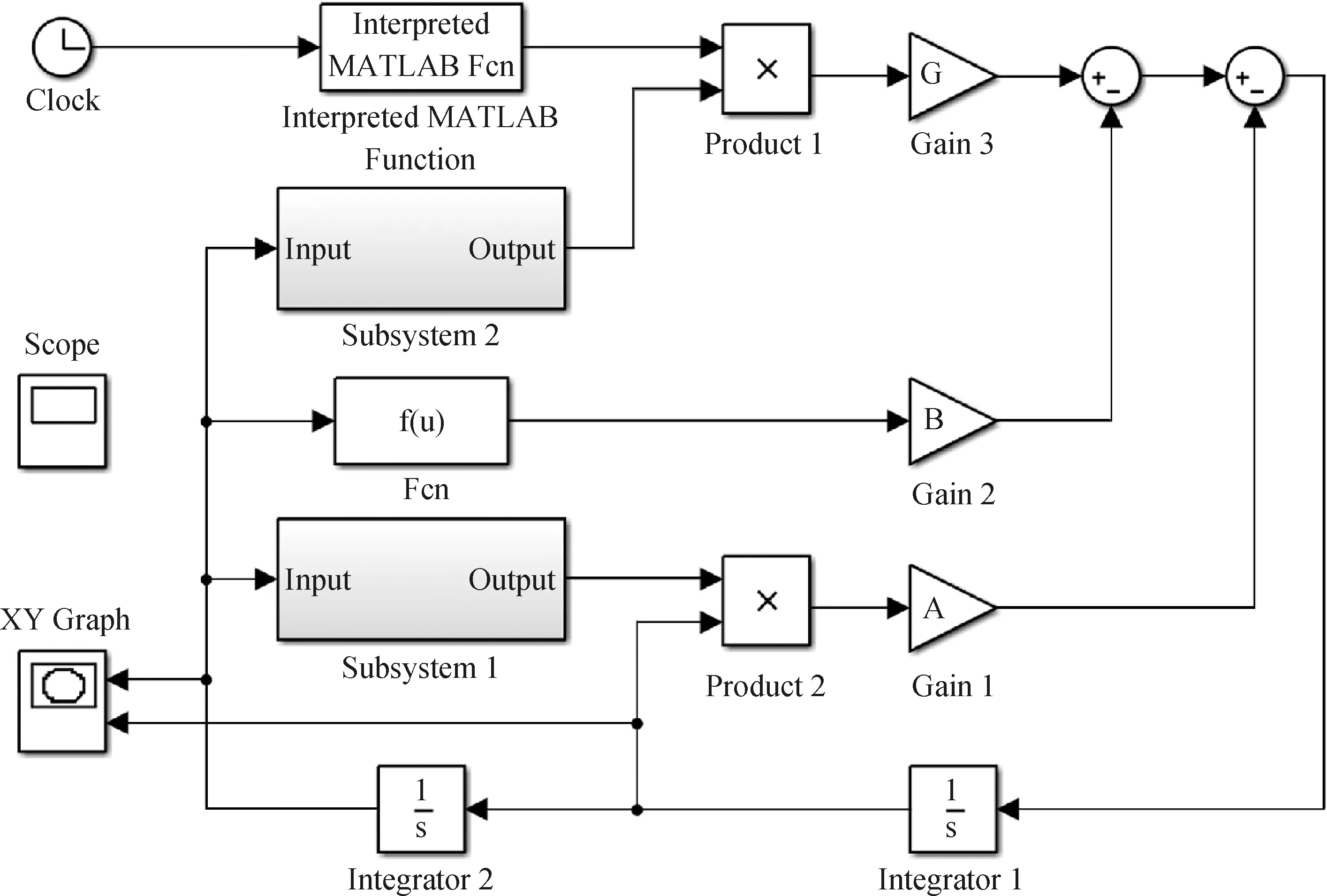
—Transfer function; Fcn—Function; A—Coefficient A; B—Coefficient B; G—Coefficient G; f(u)—Function expression圖3 乳化油液滴混沌電場振動Simulink模型Fig.3 Simulink model of chaotic electric field vibration of emulsion droplet

3 數值實驗與分析

3.1 實驗條件

設在乳化油中有一半徑R=0.6×10-3m的液滴，其密度ρ20=103kg/m3，并已知油的黏度μ20=47.2×10-3Pa·s，相對介電常數ε2=5，油-水界面張力γ= 5×10-3N/m，施加的混沌脈沖電場強度E=3×105V/m。

由式(1)、(2)可知，混沌脈沖電場的角頻率范圍主要受脈沖寬度τ和脈沖間隔上下限[Tu,Tl]的控制。脈寬τ的選取尤為關鍵，若τ取值過大，則會降低脈沖電場頻率變化上限；若τ取值過小，則會使乳化液滴難以被充分極化拉伸。所以，在進行混沌電場仿真之前，先對脈寬τ的取值進行分析。

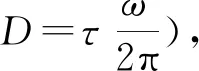
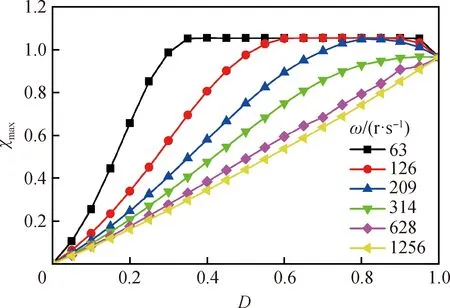
圖4 不同脈沖角頻率(ω)和占空比(D)下液滴的穩態響應幅值(χmax)Fig.4 Steady state response amplitude (χmax) of dropletunder different frequencies (ω) and duty cycles (D)

設初始混沌值a1=0.2、Tu=0.03 s、Tl=0.001 s，脈沖電場角頻率ω控制在120～300 r/s之間時，脈沖電場強度幅值及頻率變化如圖5所示。

由圖5可知，電場脈沖信號的幅值和脈寬均保持恒定且相等，脈沖間隔隨時間不斷迭代變化，使得脈沖電場的角頻率在0～1 s內混沌迭代了29次，且在120～300 r/s之間呈混沌分布。

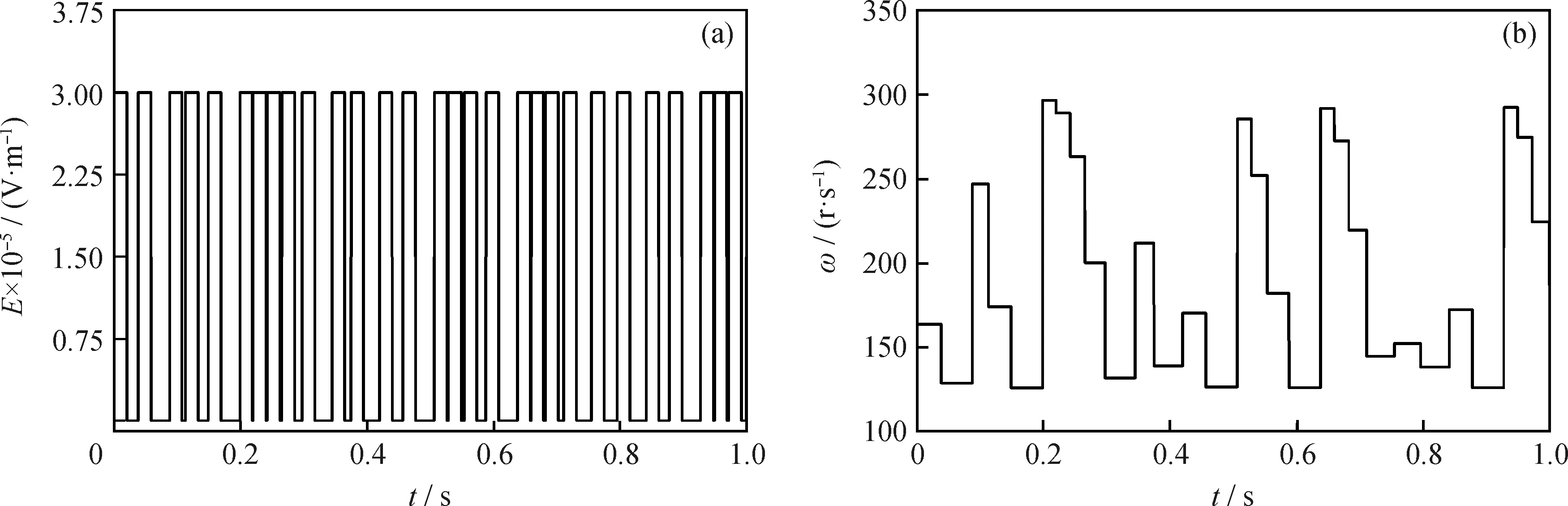
圖5 脈沖電場強度(E)與脈沖角頻率(ω)隨時間變化曲線Fig.5 Curves of pulse electric field (E) and angle frequency (ω) vs time(a) E vs t; (b) ω vs t

3.2 響應分析

通過計算，得到在1 s內混沌頻率脈沖電場中液滴的振動響應數值解，其液滴振幅與速度及各項受力曲線見圖6。

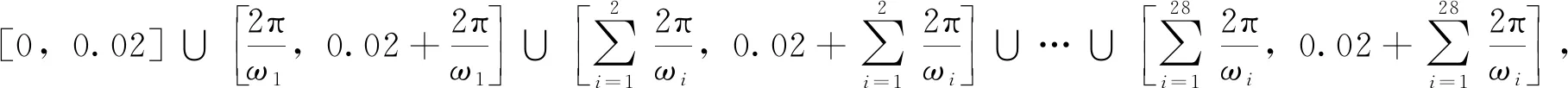
由圖7可知：在混沌電場作用下，乳化液滴每次伸縮振動周期與對應電場脈沖頻率的持續時間相等，即液滴振動響應頻率等于脈沖電場的頻率。乳化液滴的振動在高頻區出現幅值高峰，中低頻區的幅值相對較低，且波動不大。在液滴的共振頻率附近，未出現明顯的共振現象。頻率范圍越大，τ值越小，響應幅值越低，但響應曲線的變化趨勢是一致的。這是由于乳化液滴在電場中的振動受油液的阻力相對較大，自由振動不明顯，主要受電場力的策動發生伸縮振動，其響應頻率表現為與電場頻率一致。實驗采用的是等脈寬、定電場幅值的混沌頻率脈沖電場，在高頻區的低電平持續時間較短，液滴在同等時間內受電場力激勵的次數較多，故出現較大振幅；而中低頻區則反之，故振動相對穩定，但振幅不大。由于電場頻率是混沌的，永不重復，液滴的振動是非穩態的，因此尚未在共振頻率附近發現明顯的共振現象。振動系統中的初始混沌值決定了電場頻率的迭代變化，在未改變該值的情況下，響應曲線的變化趨勢也是不變的。

3.3 混沌響應

脈沖電場作用下的油中液滴振動系統本身并非混沌系統，而是引入了混沌信號的非線性系統，系統輸出是否混沌，需要對其進行混沌識別[17]。筆者采用定性和定量相結合的方法對乳化液滴在混沌頻率脈沖電場中的混沌振動進行有效識別。

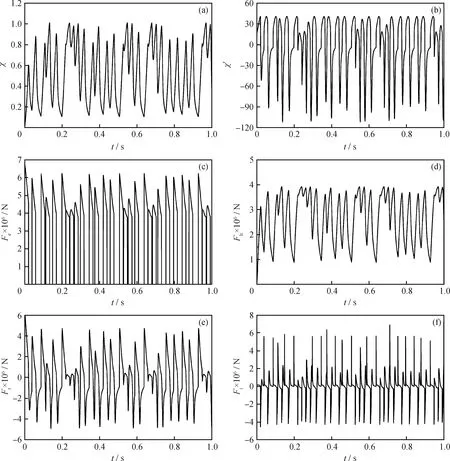
圖6 液滴振動響應幅值與速度及各項受力變化的時間曲線Fig.6 Curves of response amplitude, velocity and various forces vs time(a) vs t; (b)′ vs t; (c) Fe vs t; (d) Fh vs t; (e) Fr vs t; (f) Fi vs t

3.3.1 定性識別

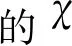
由圖8可知，相軌跡是一個不封閉的曲線，曲線無窮纏繞、折疊、永不重復，在有界區域內往復運動，符合混沌振動的特征。由此可以判斷乳化液滴在混沌電場中的振動為混沌振動。

3.3.2 定量識別

混沌運動的基本特點是運動對初始條件極為敏感[19]。在混沌運動中，2個非常靠近的初值所產生的軌道，會隨時間的推移按指數方式分離，可以通過Lyapunov指數進行定量描述，若系統最大Lyapunov指數大于0，則可以判斷混沌的存在[19]。所以，筆者選用最大Lyapunov指數來定量識別液滴的混沌振動。

首先采用C-C方法[20-21]確定仿真數據的最佳嵌入維數m和最佳時間延遲σ，再進行相空間重構，最后通過Wolf方法[22]對液滴振動響應進行最大Lyapunov指數的計算。

圖7 2種脈寬下電場角頻率(ω)和液滴振動響應幅值)隨時間的變化曲線Fig.7 Curves of electric field angle frequency (ω) and value under two kinds of pulse width vs time(a) τ=0.01 s, ω vs t； (b) τ=0.01 s, vs t； (c) τ=0.005 s, ω vs t；(d) τ=0.005 s, vs t

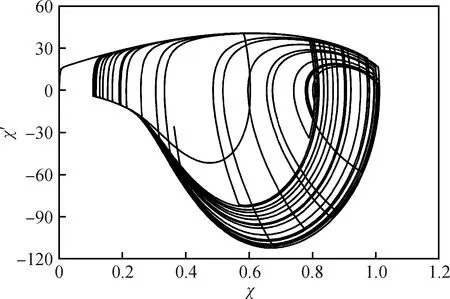
圖8 液滴振動相軌圖Fig.8 Droplet vibration phase trajectory

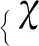
(9)

最后通過wolf方法對Y(si)的相軌線進行演化計算來估計液滴振動響應時間序列的最大Lyapunov指數L。

(10)

計算得到液滴振動響應時間序列的最大Lyapunov指數L=0.0131>0。由此可以判定乳化液滴在混沌電場中的振動為混沌振動。

4 結 論

在脈沖電場中乳化液滴的非線性振動模型基礎上，通過引入混沌信號，建立了乳化液滴在混沌頻率脈沖電場中的振動動力學模型，通過數值仿真獲得了液滴的振動響應結果，得出了以下結論：

(1)通過混沌脈沖位置調制的方法建立的乳化液滴混沌電場非線性振動動力學模型，能夠準確地描述液滴在混沌頻率脈沖電場中的振動響應情況。構建的Simulink模型能有效實現對乳化液滴振動系統的仿真分析。

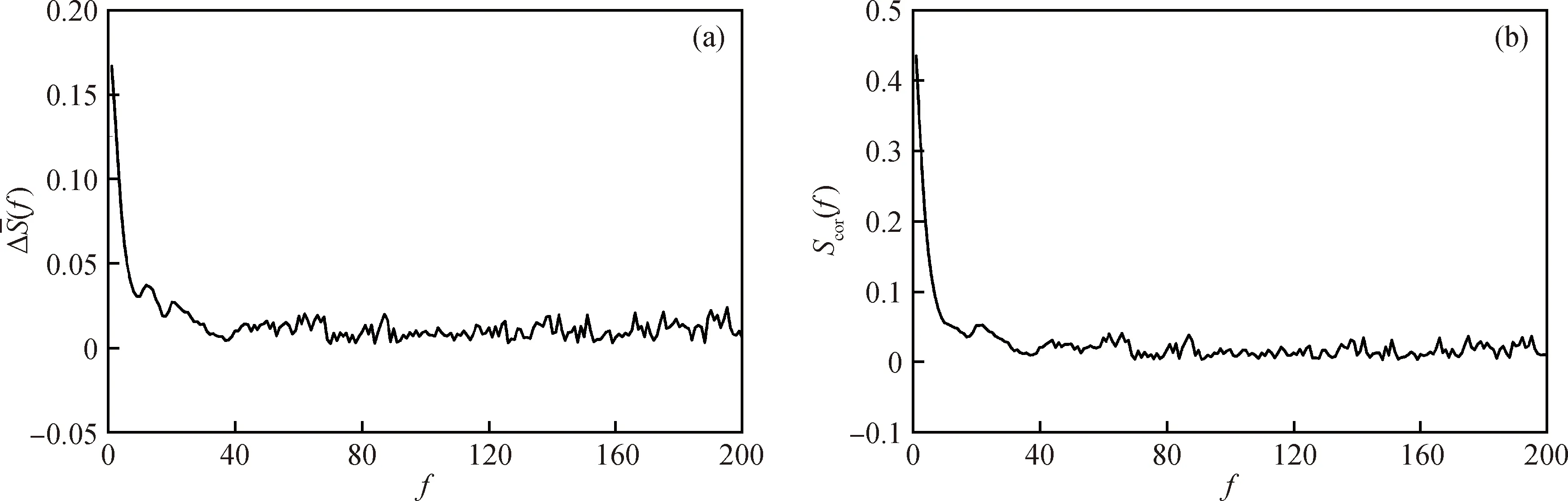
圖9 液滴振動時間序列的與Scor(f)隨采樣頻率(f)的變化曲線 and Scor(f) of droplet vibration time series vs f

(2)乳化液滴的振動受脈沖寬度的影響較大，存在最佳脈寬，振動響應在高頻區較為激烈，中低頻區相對穩定，由于頻率的混沌，液滴在共振頻率附近的響應時間較短，未表現出明顯的共振現象。

(3)乳化液滴的振動響應頻率與混沌電場頻率一致，振動相軌線有界，且無窮纏繞、永不重復，最大Lyapunov指數大于0，證明了乳化液滴在混沌頻率脈沖電場中的振動是混沌振動，進一步表明了通過引入混沌信號能夠使液滴振動系統產生混沌輸出。

(4)混沌頻率脈沖電場幅值和脈沖寬度為乳化液滴的振動提供初始動能，在脈沖寬度恒定的條件下，若幅值過小，提供給液滴振動系統的動能不足，則很難使液滴產生較為理想的振動變形量；幅值過高，會使液滴因動能過大而拉伸破裂，有悖于聚結破乳。因此，確定最佳破乳電場幅值將是下一步研究工作的重點。

符號說明：

a——振動液滴的長半軸軸長，m；

an——Logistic滿映射第n次迭代后生成的混沌值；

an+1——Logistic滿映射第n+1次迭代后生成的混沌值；

A、B、G——液滴振動方程各受力項常數；

b——振動液滴的短半軸軸長，m；

c(t)——混沌頻率脈沖電場信號函數；

di——si時刻下兩相軌小于規定值時的間距；

d′i——si時刻下兩相軌大于規定值時的間距；

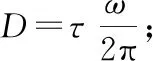
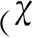
E——脈沖電場強度，V/m；

E(t)——混沌頻率脈沖電場函數；

f——液滴振動時間序列的采樣頻率；

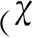
Fe——液滴振動受到的電場激勵力，N；

Fh——液滴振動受到的回復力，N；

Fi——液滴振動慣性力，N；

Fr——液滴振動受到的油液阻力，N；

K——油液阻力系數；

lx——液滴內部電勢函數；

L——最大的Lyapunov指數；

m——嵌入維數；

M——演化過程總的迭代次數，M=N-(m-1)σ；

N——時間序列長度；

R——液滴初始半徑，m；

si——相軌線演化的第i個時刻；

sM——相軌線演化結束時刻；

s0——相軌線演化初始時刻；

t——時間，s；

tn——第n個脈沖間隔，s；

Tl——脈沖間隔下限，s；

Tu——脈沖間隔上限，s；

x——笛卡爾坐標系x軸；

y——笛卡爾坐標系y軸；

Y(si)——重構相空間；

z——笛卡爾坐標系z軸；

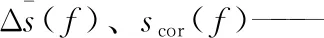
γ——界面張力，N/m；

δx——液滴長半軸伸長量，δx=a-R，m；

ε0——真空介電常數；

ε2——油液相對介電常數；

λ——液滴拉伸比，λ=a/b=(1+χ)-3/2；

μ20——油液20 ℃時的黏度，Pa·s；

ρ20——液滴20 ℃時的密度，kg/m3；

σ——時間延遲；

σw——嵌入窗，σw=(m-1)σ；

τ——脈沖寬度，s；

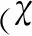
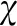
χmax——液滴振動穩態響應幅值；

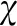
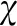
ω——周期脈沖電場角頻率，r/s；

ωi——第i次迭代后的電場角頻率，r/s。