基于車輛實際運行軌跡的平面交叉口左轉待行區模型構建

崔小強，孫春剛，蔡曉禹

(1.青海省交通規劃設計研究院有限公司，西寧 810008； 2.山地城市交通系統與安全重慶市重點實驗室，重慶 400074)

城市道路平面交叉口作為整個路網的節點與樞紐，承擔著傳遞路網交通流的作用，左轉交通流往往是影響交叉口運行效率的重要因素[1]。近年來，各平原城市通過將左轉道停車線前移、在交叉口內部安全的冗余空間設立左轉待行區等措施，以增大左轉車道容量，改善左轉車輛通行效率[2]。

GB 5768.2—2009《道路交通標志與標線》給出了左轉待行區內文字的長度、寬度及標線顏色、寬度等標準。近些年許多專家學者便對左轉待行區幾何設置條件及通行效益評價分析2大方面進行了深入研究。季彥捷[3]利用綠燈時長、到達率、車輛長度等參數對待行區設置長度進行了建模分析，結果表明合理設置左轉待行區可有效提高左轉車道的通行能力；王殿海等[4]利用車輛到達率分析了待行區設置長度與流量的臨界關系，給出了設置左轉待行區的幾何、流量、信號配時的臨界條件；金勇[5]基于排隊論對設置左轉待行區的利弊進行了詳細的分析和研究，得出左轉待行區的優缺點以及在工程設計中注意的事項；陳永恒等[6]研究了左轉待行區車輛釋放過程并建模，計算出左轉通行能力的提高值；孫冰清等[7]選取通行能力、停車延誤、停車次數等參數來評價左轉待行區設置對交通效益的影響，并通過實例得出設置左轉待行區能夠有效提高交叉口行車效率，改善運行環境。

目前，我國道路設計國標與地標中都沒有針對左轉待行區設置的量化規定，且國內外學者對左轉待行區設計方面的研究較少，使得在實際的交通工程設計中左轉待行區的設計缺乏理論依據，大多數情況下憑經驗而定[8]。為此，結合左轉車流特性特征，對其交叉口左轉待行區設置方法進行深入研究十分有必要。本文將在前人的研究基礎上，通過現場調查實際數據確定左轉車流的實際運行軌跡，并綜合考慮平面交叉口的幾何條件及避免發生車流沖突的臨界約束條件，建立基于車輛實際運行軌跡的平面交叉口左轉待行區計算模型。該模型可在平面交叉口中確定具體的左轉待行區設置參數，為后續具體的交通工程設計中提供理論依據及計算標準。

1 車輛左轉軌跡函數確定

左轉待行區的設置應根據平面交叉口的實際幾何條件進行設計，應遵循左轉車流行駛軌跡路徑要求，使左轉車流在進入、駛離左轉待行區時線形順暢、安全[9-10]。為此，本文先確定平面交叉口左轉車流的行駛軌跡，后確定左轉待行區計算模型。

1.1 車輛左轉軌跡數據獲取

本文運用無人機航拍重慶市某較典型交叉口西進口左轉車流，獲取高峰期間交叉口車輛運行狀態的原始數據[11]。為真實反映實際車輛運行軌跡，本文基于KCF跟蹤算法提取無人機視頻中的左轉軌跡數據，將左轉車流的軌跡數據導入程序，可得如圖1所示的跟蹤界面，某一輛車跟蹤結束后的軌跡數據如圖2所示。

本文提取的車輛軌跡是車輛4個頂點的數據，通過對角線函數交點計算方法可求得左轉車輛對角線交點坐標信息，即車輛中心數據。本次調研共獲得有效樣本200個。

1.2 左轉軌跡擬合函數分析

為有效表達左轉車流軌跡運行的實際情況，需要充足的車輛左轉軌跡信息，通過函數擬合的形式，確定相關系數較大(一般相關系數R2≥0.9表示擬合效果理想)的函數作為車輛左轉軌跡的函數原型[12-13]。

圖1 左轉車輛跟蹤窗口示例

圖2 某一輛車左轉軌跡

左轉車輛在交叉口內部的運動過程大致可描述為：通過建立直角坐標系，車流軌跡在停車線處的導數趨近于0，隨著車輛的運行，在車輛軌跡結束點處的軌跡導數趨近于無窮大[14]。據此特性，對照已知數學函數模型，初步判斷出線性曲線函數中的二次函數、指數函數和單項指數衰減函數等3種函數，其模型公式分別為：

二次函數：y=ax2+bx+c

(1)

指數函數：y=meλx

(2)

單項指數衰減函數：y=A1e(-x/t1)+y0

(3)

式中：a、b、c、m、A1、t1、y0均為二次函數、指數函數、單相指數衰減函數等擬合函數中的參數值。

本次擬合試驗利用基礎試驗工具Matlab分別對包括線性曲線函數和非線性曲線函數在內的3種符合交叉口左轉車流運行特性的曲線函數進行擬合，如圖3所示。圖3中，橫縱坐標均為左轉車輛在x軸與y軸的相對距離，單位為mm。試驗結果表明：非線性曲線函數中的單相指數衰減函數的相關系數均值明顯高于其它2個擬合曲線函數，故選擇非線性曲線函數中的單相指數衰減函數作為本次交叉口車輛左轉軌跡的基礎擬合函數。3種擬合曲線函數對部分左轉軌跡數據的擬合結果如表1所示。

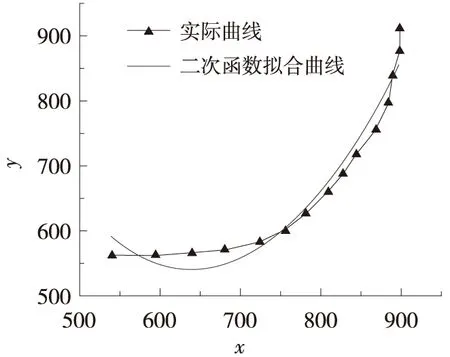
(a) 二次函數

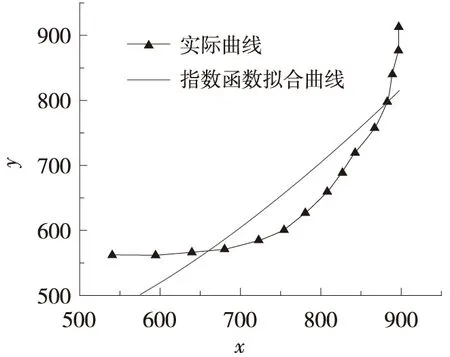
(b) 指數函數

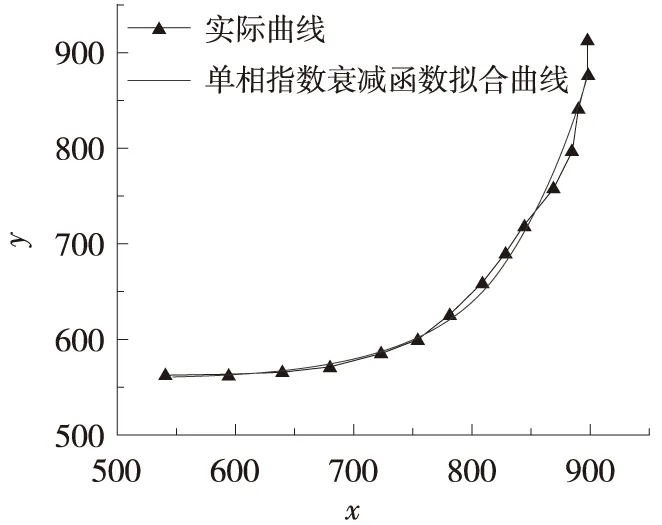
(c) 單相指數衰減函數

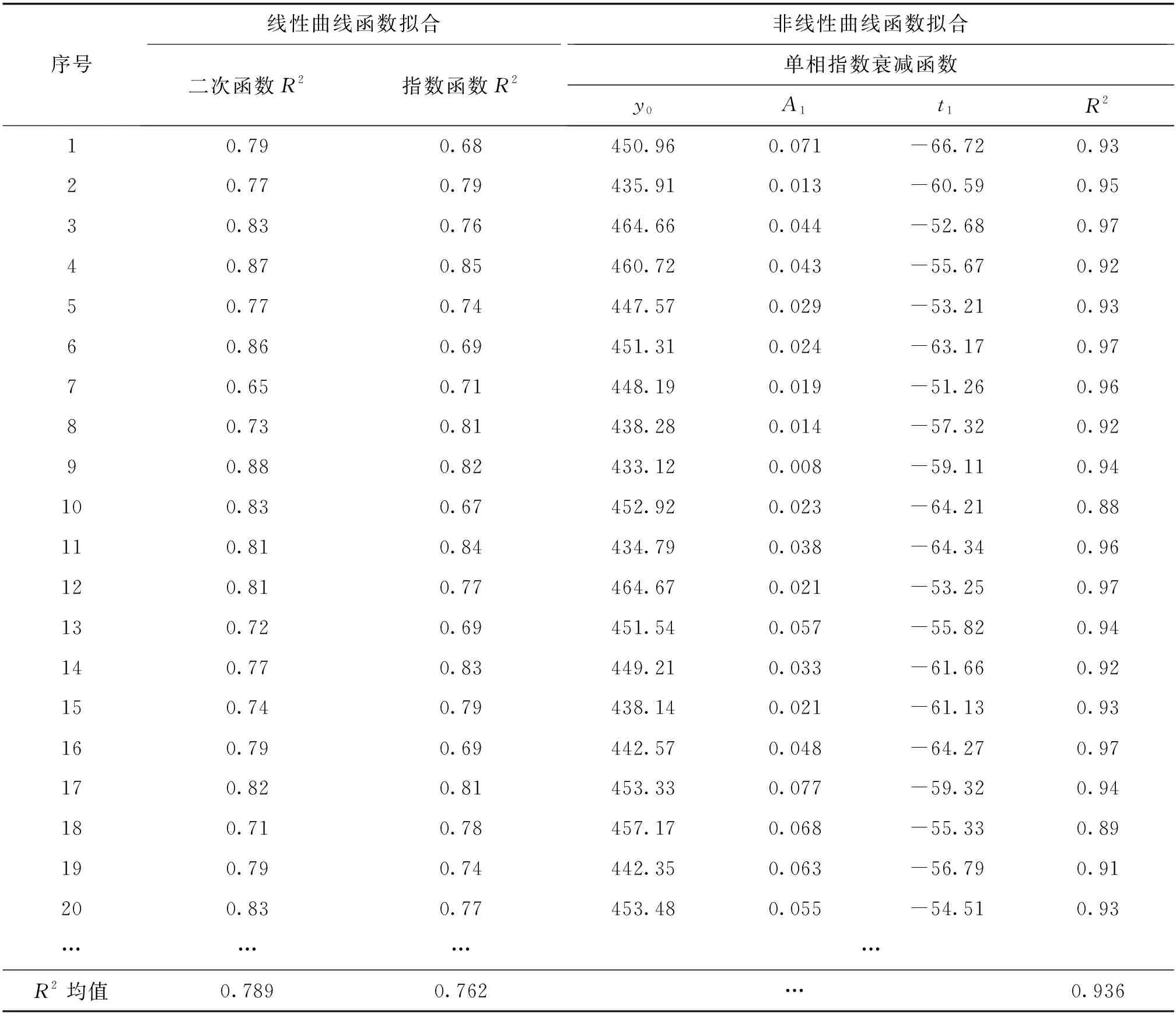
表1 左轉軌跡擬合結果

1.3 左轉軌跡目標擬合函數確定

由表1可知，二次函數、指數函數和單相指數衰減函數的擬合相關系數分別為0.789、0.762和0.936。一般研究表明，當相關系數大于0.9時擬合效果較優，為此，確定以單相指數衰減函數作為交叉口左轉車輛軌跡的目標擬合函數，即

y=A1e(-x/t1)+y0

(4)

2 構建車輛實際運行軌跡的左轉待行區模型

2.1 確定交叉口幾何參數

由于左轉待行區的設置與平面交叉口的幾何參數有著密切的關系，為了準確表示出左轉待行區與交叉口幾何條件之間的關系，利用人工調查的方法，確定了重慶某典型交叉口內部相關幾何參數數據，如圖4所示，為后續模型建立奠定數據基礎。

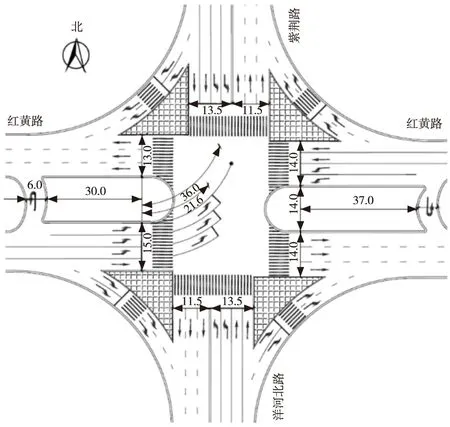
單位：m

2.2 車輛左轉軌跡的約束條件

1) 左轉軌跡轉向起點約束

左轉軌跡轉向起始點為交叉口左轉車輛在綠燈時間內通過停車線時的位置[14]。交叉口進口道左轉車道的車道寬度一般為3.0 m和3.25 m，在保證車輛安全通行的條件下，盡量限制車輛通過交叉口的速度。本文在左轉車輛軌跡模型構建過程中，左轉車輛通過交叉口停車線的位置取車道的中心位置，即坐標系的原點位置；交叉口南進口道一個左轉車道寬度為x4，如圖5(a)所示，則左轉軌跡起點的坐標為(0，0)。

2) 左轉軌跡轉向訖點約束

車輛左轉軌跡轉向訖點是左轉車輛轉彎結束及駛離交叉口的位置。理想狀態下，交叉口最內側進口道左轉車輛轉彎駛離交叉口時，從出口道最內側車道駛離效果最佳[15]，但在實際狀態下，駕駛員駕駛車輛時為了減小轉彎過程中車輛離心力的影響，在駕駛過程中會增大車輛轉彎半徑，從交叉口出口道最內側車道、內側第2車道、內側第3車道等可選擇性地駕駛通過交叉口，因此在對左轉軌跡轉向訖點進行約束時，需分情況討論。交叉口南進口道至車輛轉向結束點的橫向距離(即x軸方向的距離)為x5，車輛從最內側車道駛離時坐標軸原點至轉向結束點(從出口道最內側車道駛離)的縱向距離(即y軸方向的距離)為x2，車輛從最內側車道駛離時坐標軸原點至轉向結束點(從出口道最內側一、二車道標志線駛離)的縱向距離(即y軸方向的距離)為x2+x6，如圖5(a)所示，則左轉軌跡轉向訖點坐標為(-x5,x2+x6)。

3) 左轉軌跡轉向沖突限制點約束

在左轉車輛轉向過程中除了受到轉向起訖點的約束之外，還受到左轉軌跡轉向沖突點的限制約束，避免左轉車輛與對向直行車輛發生沖突。

左轉軌跡轉向沖突限制點是指到左轉相位綠燈亮啟時左轉頭車與對向直行尾車發生沖突的潛在約束限制點[16]。根據“左轉車輛讓行直行車輛”的原則，在左轉軌跡模型構建過程中，應當使左轉頭車到達潛在沖突點的距離不短于直行車輛到達潛在沖突點的距離，從而使左轉頭車到達沖突點的時刻晚于對向直行尾車，從時間和空間上進行限制，使沖突點的隱患降到最低，如圖5(a)所示。左轉車流與對向直行車流的沖突點為C點，當左轉車流軌跡到達沖突點的距離與對向直行車輛到達沖突點的距離相等時為發生沖突的臨界條件[17]。直行車流的軌跡趨近于直線，而左轉車流的軌跡是一個弧形。當左轉車流行駛至沖突點的理論直線距離(即左轉弧線的弦長)恰好與對向直行車輛行駛至沖突點的距離相等時，即可保證左轉車流實際到達沖突點的曲線距離大于對向直行車輛的直線距離(弧長總是大于弦長)。為此，令左轉車流起點至沖突點C的縱向距離(y軸方向的距離)為y；交叉口南北向停車線之間的距離為x3，則對向直行車流到達沖突點C的距離和左轉車流起點至沖突點C的直線距離均為x3-y；對向直行車流起點至左轉車流起點的橫向距離(x軸方向的距離)為x1，如圖5(a)所示，建立左轉起點至沖突點的三角函數關系，則有

x12+y2=(x3-y)2

(5)

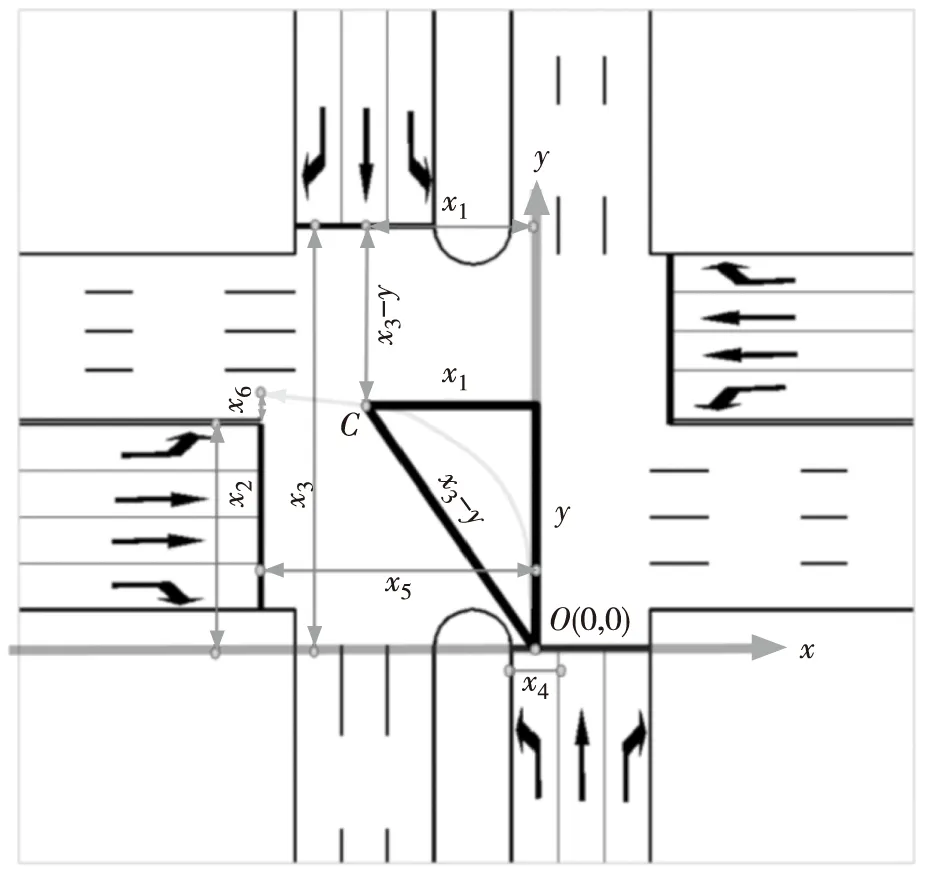
(a) 左轉車流在交叉口內部軌跡

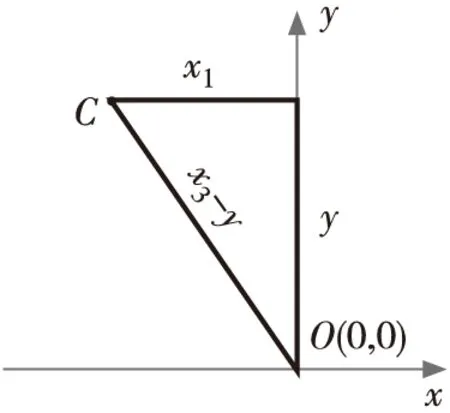
(b) 軌跡長度關系

根據公式(5)，函數變換可解得：

(6)

根據圖5(b)中坐標系，可得到沖突點C的坐標數據，即

(7)

由左轉軌跡目標擬合函數公式(4)可知，其存在3個系數，分別為A1、t1、y0，則需確定關于3個系數的關系公式。分別將關系條件公式(5)～(7)帶入左轉軌跡目標擬和函數公式(4)中，即可求解出3個系數分別為：

(8)

(9)

(10)

2.3 基于曲線線性識別法構建左轉軌跡分段模型

1) 左轉軌跡曲線線形識別

本文基于公路線性識別計算方法的啟發，對交叉口左轉車流軌跡曲線進行線性識別，能夠更加詳細地判別出軌跡曲線各線段的線形，便于構建基于左轉軌跡線段長度的分區間模型函數。本次研究分別對重慶市典型交叉口進行調查，計算并驗證了左轉軌跡分段模型。根據左轉車流曲率計算結果，繪制左轉車流軌跡曲率，如圖6所示。

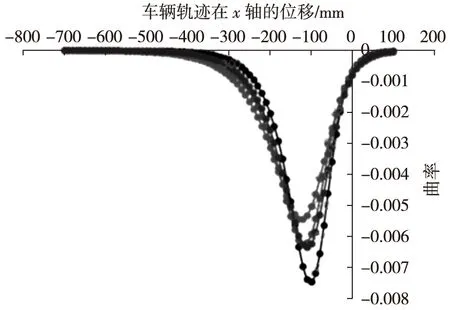
(a) Matlab中曲率分析

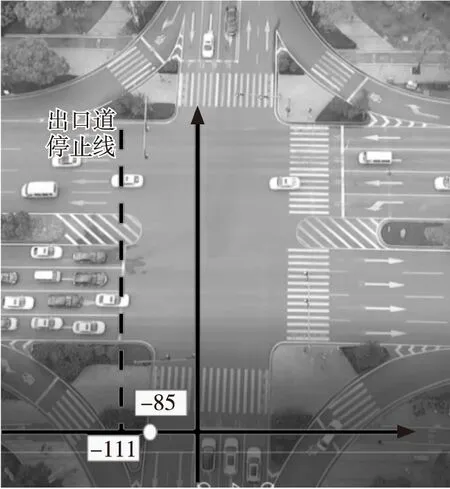
(b) 交叉口拐點示意

分析圖6(a)可知，處在直線段處的曲率區間均在1 m之內，即圓曲線區間在1 m之內，考慮到車輛實際尺寸平均為5.5 m，圓曲線1 m在可忽略的范圍之內，則基本可確定左轉車流軌跡函數模型由直線和緩和曲線組成。

2) 構建分段軌跡分段函數模型

基本可由交叉口的幾何靜態數據計算出車輛左轉軌跡的函數模型，對軌跡函數進行曲率識別可判斷出軌跡拐點，即可進行左轉軌跡的分段建模[18]。由公路線形特性可知，緩和曲線的函數模型為回旋線函數模型，模型的基本形式如下：

(11)

式中：A為回旋線函數模型參數；R為緩和曲線終點曲線半徑值；LS為緩和曲線的長度。

由緩和曲線的基本函數模型變換后，可得出以緩和曲線長度為自變量、半徑為應變量的新型函數模型公式：

(12)

式中：參數A可由緩和曲線長度計算得到，假設左轉車流軌跡緩和曲線的拐點在x=m處，左轉車流終點為n；Lx可由軌跡函數取極限求得，具體模型公式為：

(13)

式中：p(xj)為左轉軌跡函數模型f(xj)-f(xj-1)；Ti為左轉軌跡函數模型自變量xi-xi-1。

將公式(13)帶入新型函數模型公式(12)中，可得到左轉軌跡的分段函數模型公式為：

(14)

3) 確定左轉待行區模型

目前，已知了左轉車流的軌跡模型，根據設置待行區的進口道左轉車流軌跡與對向直行車道車流軌跡的沖突點C，可確定左轉待行區內車輛軌跡的模型，左右平移可構成待行區，其平移區間寬度為左轉車道寬度，如圖7所示。圖7中，Ls為安全間距。

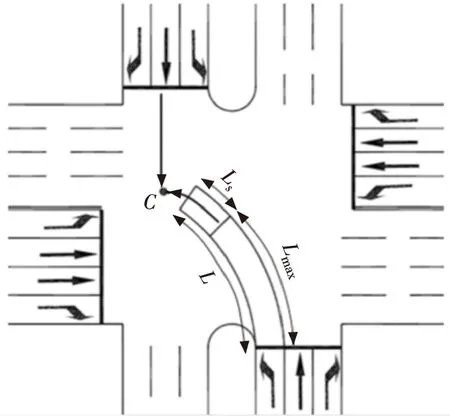
圖7 左轉待行區設置示意

3 實例分析及仿真

3.1 Vissim微觀仿真建模

為了能夠真實反映交通現狀條件，需將現狀CAD圖作為底圖導入Vissim軟件中，并需將其比例縮放為現狀真實比例，以便下一步仿真模型的構建。根據微觀仿真模型構建原則，依次通過車道布設、路徑分配、流量輸入、信號配時方案輸入等步驟建立交叉口模型，如圖8所示。

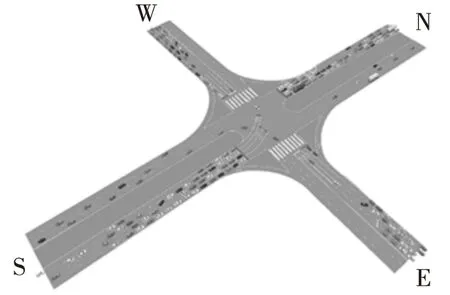
圖8 交叉口仿真模型構建示意

3.2 交叉口左轉待行區參數計算

根據交叉口幾何數據可得：x3=43 m,x1=24.5 m,x4=3.5 m,x2=23.5 m,x5=35 m，其中包括人行道寬度6 m和停車線至人行道斑馬線的距離2 m。帶入模型公式則可求出：A1=13.334 9；t1=-68.422 4；y0=-1.566 609 42E-97。其中y0為接近無窮小值，可忽略不計，帶入模型公式(4)中，可得該交叉口左轉軌跡模型為：

(15)

對模型公式(15)進行曲率分析，發現曲率拐點發生在x=25 m處。求出拐點與沖突點的位置，即已知了左轉車流分段函數模型界限，只需求得分段緩和曲線的參數A和各自的長度即可求解分段函數軌跡模型。

求解左轉待行區內左轉車流軌跡分段函數長度：在城市平面交叉口中車輛多為小汽車，其實際平均寬度為5.5 m，本文中取積分間距為1 m即可滿足積分要求。假設L1和L2分別為左轉待行區內左轉車流軌跡分段函數長度，則有

L1+L2=38.657 8

根據沖突點位置以及進口道坡度大于5%，從交叉口車輛運行安全角度考慮，基于車輛實際運行軌跡的待行區的最長長度為：

Lmax=L-

38.657 8-

30.347 8 m

3.3 結果分析

為了驗證待行區最大長度設置模型的有效性，分別構建了不同待行區長度下的交叉口Vissim模型，其仿真統計結果如表2所示。交叉口距離參數由圖5可得，模型仿真車輛連續監控運行時長定為3 600 s。

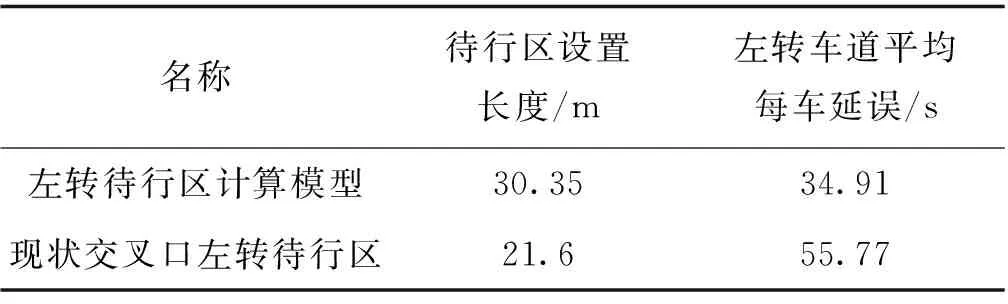
表2 Vissim仿真統計結果

由表2可知，現狀待行區長度為21.6 m，其左轉車道平均每車延誤為55.77 s；基于車輛實際運行軌跡的待行區長度為30.35 m，左轉車道平均每車延誤為34.91 s，相比于現狀待行區長度，平均每車延誤下降了37.4%，這說明保證行車安全的前提下，待行區長度越長，左轉車輛在同一信號周期內釋放的車輛越多，左轉車道平均每車延誤越小。

4 結束語

1) 基于無人機視頻跟蹤技術獲取重慶市幾個典型交叉口左轉車流的軌跡數據，利用MATLAB軟件對獲取的左轉車輛軌跡數據進行軌跡擬合，通過對比相關系數值，發現單相指數衰減函數的相關系數R2均值最大，達到了0.936，即確定該函數為左轉軌跡擬合函數，y=A1e(-x/t1)+y0。

2) 通過建立起點、訖點、沖突限制點3個約束條件，構建了關于交叉口幾何尺寸關系的左轉軌跡函數模型，并通過曲線識別法分析出左轉軌跡是由2段不同的緩和曲線組成，并分別建立了2段關于軌跡半徑與緩和曲線長度的函數模型。

3) 根據左轉軌跡與對向直行車輛軌跡產生的沖突限制點約束和安全距離的限制，構建出左轉待行區函數模型，并通過實例進行了驗證，試驗結果表明本文模型對平面交叉口左轉待行區的設置有一定的借鑒作用。

然而本文計算模型僅針對十字正交交叉口，對于畸形等不規則交叉口無法適用，且未考慮行人過街影響，在后續的研究中將重點分析此類情況，以完善適用于各類情形的平面交叉口左轉待行區模型。