索輔梁拱塔斜拉橋體系受力研究

馬振棟，陳家勇，賴亞平

(林同棪國際工程咨詢(中國)有限公司，重慶 401121)

纜索承重橋梁中，纜索是提供整體剛度及承載受力的主要構件，梁體主要起提供局部剛度、傳遞活載的作用[1]，因此梁體向更輕型化發展，梁高與跨度的比值(高/跨比)隨著主跨的增大呈減小趨勢，如現代大跨度斜拉橋的高/跨比一般為1/100～1/300，甚至更低[2-3]。當橋梁主跨為80 m～300 m且梁體自身具有較大的承載能力時，按纜索承重橋梁設計就會使梁體的承載能力發揮不足，為解決這個問題，鄧文中院士在2007年提出了“以梁為主體，纜索承重為輔的索輔梁橋”的理念，即把充分發揮梁體自身的承載能力作為前提，把纜索設計成為輔助受力的結構[4-6]。索輔梁橋是較為新型的橋梁類型，在應用實踐中，常面臨2個典型的問題：1) 在選定的梁高下，纜索需要承受多少比例的總荷載(承載比)、采用何種類型及布置方式的纜索來輔助梁體受力才能滿足跨度的要求；2) 怎樣利用“纜索為輔助受力結構”這個特點進行輕型化的索塔設計，索塔架設對工法有何要求。為解決這2個層面的問題，以四川眉山岷江大橋為例，研究纜索的承載比、選用類型及布置方式，對輕型化、全曲線造型的拱塔及輔塔進行受力影響分析，對經結構優化后大橋的合理性做出評價，并與同類型的拱塔斜拉橋—沈陽三好橋對比,總結各自的結構特點[7]，對拱塔施工提出工法上的建議。

1 橋梁總體布置

四川眉山岷江大橋是舊址新建工程，原橋址因長期采砂使得河床下降，導致橋墩基礎沖刷嚴重、喪失承載能力而拆除。

新建的岷江大橋跨徑布置為(37.5+39+55+120+120+55+39+35)m=500.5 m，整體為一聯，橋寬32.5 m。由于通航高度、路線高程及工程投資限制，梁體采用梁高為2.5 m的預應力混凝土扁平箱梁。建設方要求新橋需具有輕巧的拱結構元素以體現橋梁與岷江兩岸“青山綠水相融合”的城市風貌，因此采用了拱塔斜拉橋方案，如圖1所示。

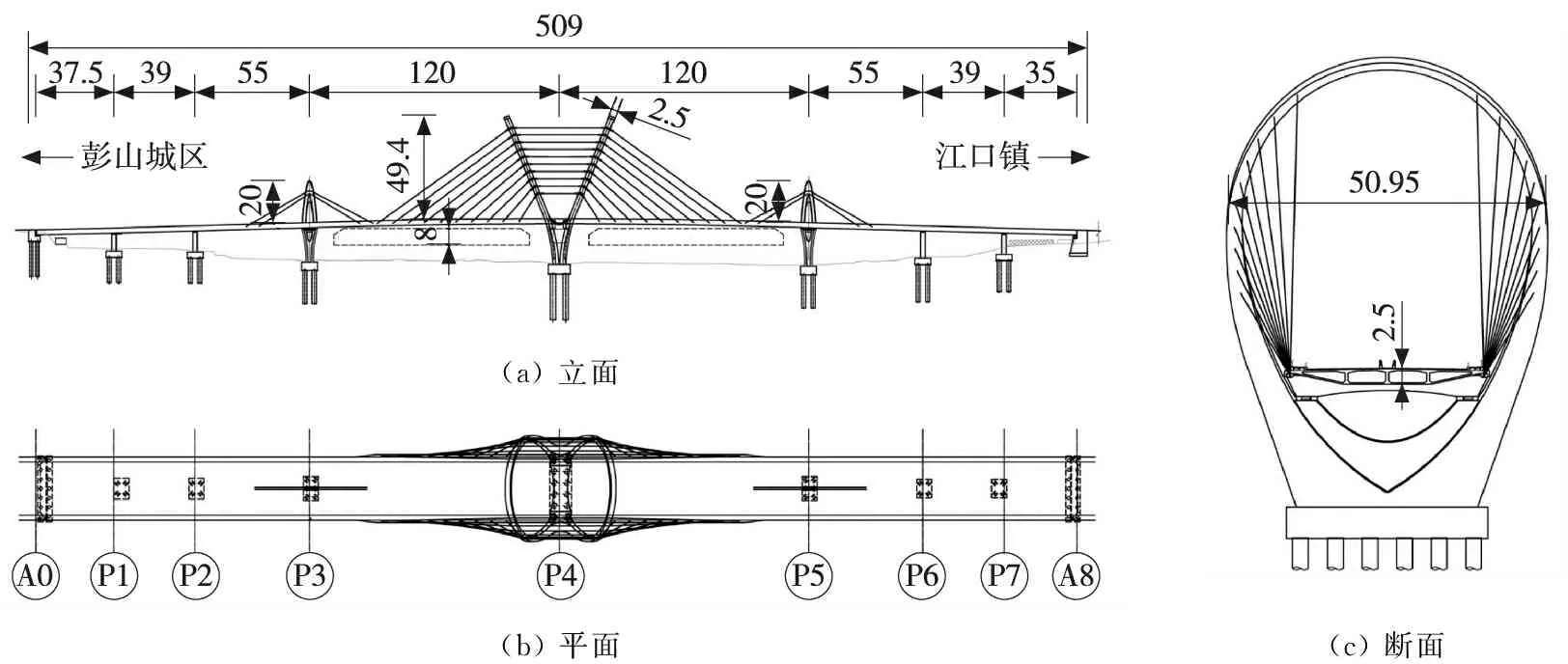
單位：m

2 承載比及纜索類型研究

利用數值分析法，推導在梁高為定值時，纜索的承載比、類型與跨度之間的關系公式，梁體彎矩基本公式為：

M=λpL2

(1)

式中：p為總荷載，kN/m；L為計算跨徑，m；λ為與結構體系相關的系數[8]，如簡支梁λ取1/8。

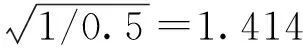
(2)

式中：L輔為采用纜索輔助后可達到的跨徑，m；L梁為該梁體用在梁式橋時的跨徑，m。

將梁體的承載比代入并考慮纜索類型的影響，得出跨度經驗公式：

(3)

式中：η為梁體承載比；K為綜合系數。按照纜索的作用原理不同，有2種類型要考慮：1) 設置垂直吊索時，直接考慮吊索在豎向對梁體提供的支撐作用；2) 纜索為斜拉索時，它不僅在豎向對梁體提供了支撐，纜索力的水平分量還增加了預應力混凝土梁體的壓應力，起到優化梁體受力、提升跨越能力的作用，因此K按下述規律選取：設置垂直吊索時K=1.0，設置斜拉索時K=1.3～1.6，按η取值越高，K值取值越低的規律插值。

利用公式(3)對2.5 m高的預應力混凝土梁體按纜索的承載比(η纜索=1-η)30%～70%分階，考慮采用斜拉索及垂直吊索2種類型進行多參數分析，得到纜索承載比、纜索類型與跨度之間的關系，如圖2所示。

圖2 纜索承載比與跨度關系

由圖2可知，纜索對跨度的提升作用呈現出隨纜索承載比的增加而增長的趨勢；因斜拉索的水平分力對預應力混凝土梁體的優化受力作用，故呈現出斜拉索對跨度的提升能力比垂直吊索高出 30%～60%的趨勢。采用斜拉索輔助且跨度要求為120 m時，斜拉索的承載比取值約為60%。采用垂直吊索輔助且同樣承載比為60%時，跨度只能達到80 m，即使在承載比達到70%，跨度也只能達到90 m，但在纜索承載比超過70%后，纜索成為承載受力的主要構件，與索輔梁橋的基本概念不符。因此，同樣承載比時，斜拉索比垂直吊索對跨度的提升作用更為顯著。

岷江大橋由于通航高度、路線高程的限制，如采用垂直吊索，只有下承式拱橋能滿足要求，但即使采用鋼結構拱肋，其體量也較為龐大且需額外設置水平系桿[9]，除增加梁體設計難度外，也與建設方對橋梁形體的要求不符。綜上所述，采用承載比約60%的斜拉索輔助梁體受力，可滿足岷江大橋120 m的跨度要求。

3 索塔受力影響分析

3.1 橋梁有限元建模

為研究鋼拱塔及輔塔對索輔梁橋結構受力的影響，采用有限元程序Midas Civil對全橋進行建模。對主梁采用三維梁單元模擬、輸入所有預應力效應，以主梁滿足全預應力構件為基本前提[8]；拱塔、輔塔、塔座、塔墩等采用三維變截面梁單元模擬；樁基礎采用三維梁單元模擬，用土彈簧系數模擬樁土間的相互影響；拉索用只受拉的桁架單元模擬[10]。模型共2 457個節點、2 319個單元，有限元模型如圖3(a)所示，靜力荷載包括自重、二期恒載，汽車及人群活載以移動荷載方式施加。

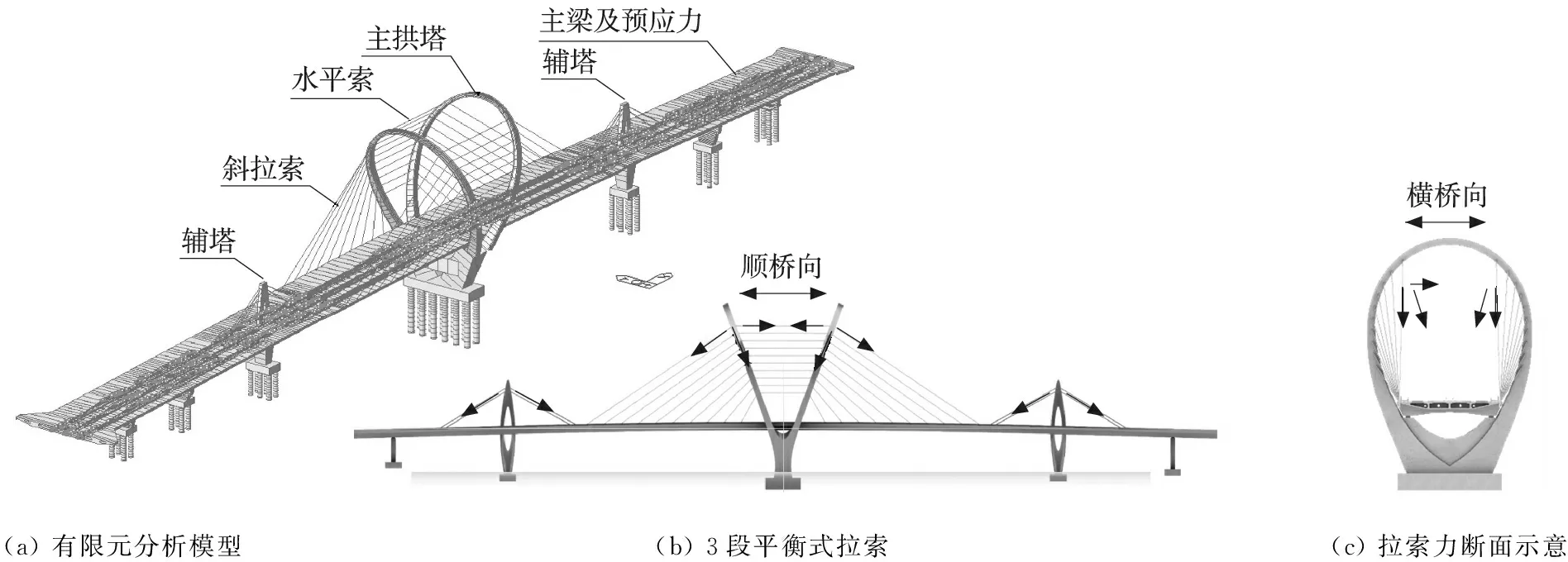
(a) 有限元分析模型 (b) 3段平衡式拉索(c) 拉索力斷面示意

3.2 P4鋼拱塔受力影響分析

P4為雙肢鋼拱塔構造，設置斜拉索和與之對應的水平索構成了3段平衡式拉索，如圖3(b)、(c)所示。為達到梁體和鋼拱塔受力最優的目的，3段平衡式拉索要求斜拉索與水平索的索力一致、索體選用同一型號。雙肢拱塔間的夾角是重要的參數，它決定著斜拉索與水平索的合力是否位于拱肋平面內，即決定著“3段平衡式拉索”的設計目的能否實現，因此在其他結構參數不變的情況下，通過研究雙肢拱塔間不同的夾角對拱塔結構及主梁的應力影響，確定出結構影響的敏感性及應力的變化規律。

拱腳處為內力最大位置，且隨著拱塔間夾角的變化其結果變化較大，因此將拱腳處的應力作為控制目標1；P4鋼拱塔處主梁是梁體負彎矩最大位置[11]，且隨著拱塔間夾角的變化其結果也會變化，因此將P4鋼拱塔處主梁頂緣的應力作為控制目標2。

雙肢拱塔間夾角在36°～52°時拉索合力鄰近拱肋平面，故以該角度區域作為研究范圍，計算出控制目標隨著角度變化的取值，從而得出一系列的控制點并用圖形表示，經分析比較得出變化規律，對P4雙肢拱塔間夾角取值給出建議。

3.2.1 P4拱腳處應力變化規律

P4拱腳處應力的變化規律如圖4所示。

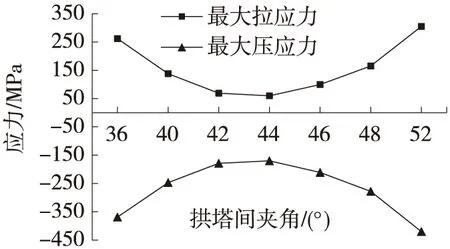
圖4 P4拱腳處應力變化規律

由圖4可知，P4拱腳處應力為受拱塔間夾角變化影響顯著的目標值，在夾角由36°～52°變化時呈現出大曲率的曲線變化規律，最大拉應力及壓應力曲線均在44°附近為極小值，表明該角度趨近于拱塔間的最佳角度；角度由44°逐漸減小及增大時，應力變化幅度均較大，在39°及48°附近應力均超過規范允許值；因此拱塔間夾角在39°～48°時屬于合理的角度范圍。

為達到拱塔受力優化的目的，岷江大橋拱塔間夾角取值應在44°附近優化，拱腳處應力可控制在最大拉應力80 MPa、最大壓應力-180 MPa。

3.2.2 P4鋼拱塔處主梁頂緣應力變化規律

P4鋼拱塔處主梁頂緣應力的變化規律如圖5所示。

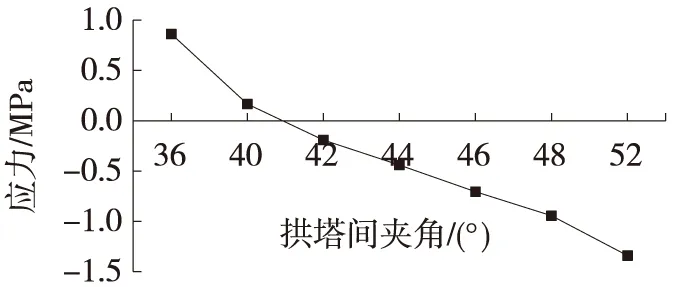
圖5 P4鋼拱塔處主梁頂緣應力變化規律

由圖5可知，P4鋼拱塔處主梁頂緣應力也是受拱塔間夾角變化影響顯著的目標值，在夾角由36°～52°變化時，應力呈由拉應力向壓應力逐漸轉化的規律，變化速率基本一致，且在夾角41°～52°范圍，梁體可滿足全預應力要求。壓應力逐漸增加的原因是隨著拱塔間角度的增大，斜拉索與水平線的夾角逐漸小幅減小，在拉索豎向承載比不變的情況下，斜拉索水平分力的增大增加了梁體的壓應力。岷江大橋拱塔間夾角可在41°～52°范圍內優化取值。

3.3 P3、P5輔塔受力影響分析

因2.5 m的梁高用在連續體系時最大跨度只能達到50 m，顯然邊跨55 m的跨度需要部分纜索支撐輔助受力，需由輔塔的斜拉索提供。因此，輔塔斜拉索的作用及設置數量是重要的參數。在其他結構參數不變的情況下，通過研究P3、P5輔塔是否設置斜拉索及設置數量，確定出結構影響的敏感性及應力的變化規律。P3、P5輔塔處(即邊跨支點處)主梁是負彎矩顯著的位置，是否設置斜拉索及設置數量對其影響很大，因此取該處主梁頂緣應力作為控制目標1；P4拱塔處主梁頂緣應力和拱腳處應力是整個結構最應關注的關鍵目標，因此分別作為控制目標2和3。

以P3、P5輔塔不設置斜拉索、設置1對斜拉索、設置2對斜拉索這3種情況作為研究范圍，計算出控制目標隨之變化的值，從而得出一系列的控制點并用圖形表示，經分析比較得出變化規律，并對岷江大橋P3、P5輔塔是否需設置斜拉索及設置數量給出建議。

3.3.1 控制目標1和2處應力的變化規律

因全橋對稱，故取P3處主梁頂緣應力代表控制目標1，控制目標1和2處應力的變化規律如圖6所示。

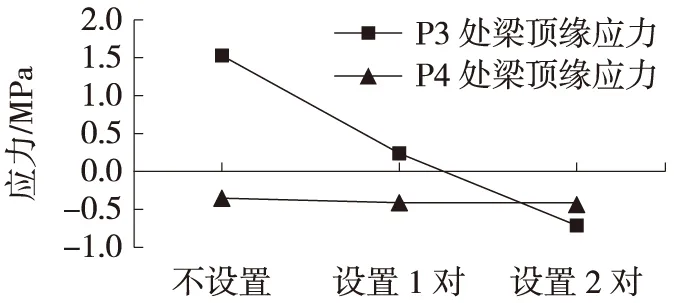
圖6 P3、P4鋼拱塔處主梁頂緣應力變化規律

由圖6可知，P3輔塔處主梁頂緣應力為受影響顯著的目標值，不設置斜拉索時不滿足全預應力要求，設置1對即改善1.3 MPa、但仍不滿足全預應力要求，設置2對可改善2.3 MPa、滿足全預應力要求。P4鋼拱塔處主梁頂緣應力為受影響微弱的目標，從不設置斜拉索到設置2對拉索僅改善0.1 MPa，因此不作為主要控制目標。岷江大橋輔塔處需設置2對斜拉索以保證邊跨梁體滿足全預應力構件的要求。

3.3.2 鋼拱塔拱腳處應力變化規律

鋼拱塔拱腳處應力的變化規律如圖7所示。

圖7 P4鋼拱塔拱腳處主梁頂緣應力變化規律

由圖7可知，鋼拱塔拱腳處應力為受影響微弱目標，從不設置斜拉索到設置2對拉索僅改善5 MPa。因此，應以輔塔處主梁頂緣應力為主要控制目標。

4 全橋構造合理性評價及工法研究

4.1 全橋構造合理性評價

岷江大橋按研究所得結論進行如下優化：P4雙肢鋼拱塔間夾角取值43.6°，每側設置10對斜拉索和10對水平索構成平衡拉索，型號均為15-55；輔塔設置2對15-31型斜拉索；對Midas Civil程序所建的全橋有限元模型進行對應修改，分析所得的主要結果如表1所示。

表1 大橋主要分析結果 MPa

由表1可知，成橋狀態主梁及拱塔應力比較理想，斜拉索及水平索內力較為一致。活載作用下，主跨的撓/跨比為1/2 521，拱塔面內及面外變形小于21 mm、應力小于14 MPa，纜索內力小于總內力的6.3%，說明梁體自身剛度大，起到主要承載作用。使用狀態下，斜拉索豎向分力承受62%的總荷載，與數值分析法所得結論一致，主梁滿足全預應力構件的設計要求，自身承載能力充分發揮，鋼拱塔應力水平占規范允許值的67%。表1分析結果表明3段平衡式拉索設計使各構造協同受力，充分發揮各自的承載能力，全橋結構合理、受力安全。

筆者主持設計于2008年建成通車的沈陽三好橋亦為拱塔斜拉橋，與眉山岷江大橋相比，各自的特點如表2所示。

由表2可知，岷江大橋采用了形體更輕型化、全曲線造型的拱塔，利用3段平衡式拉索與輔塔斜拉索組合起到了更有效的輔助受力作用，使拱塔、輔塔、主梁達到更佳的協同受力效果，滿足了跨度更大、梁體設計等級更高的要求。

4.2 拱塔架設工法研究

調查發現橋位處江面寬闊、水流湍急，不具備搭設70 m(江面～塔頂)高的大型支架來拼裝拱塔的條件，建議拱塔采用“同步對稱豎轉”施工工藝；58 m高的拱塔是輕型化的柔性結構，豎轉施工過程中的受力控制是關鍵因素。為研究這個問題，采用有限元程序Midas Civil建模進行受力分析、采用BIM建模進行空間關系研究，模擬施工中牽引起吊、旋轉過程、拱腳固結、拉索安裝等關鍵工序和是否存在空間沖突問題[12]，如圖8所示。

分析得出“同步對稱豎轉”施工過程中拱塔受力安全，但實施中須注意的事項為：1) 鋼拱與塔座連接處需設計為轉動軸，注意保證拱塔兩端轉動軸同心共線；2) 豎轉基本到位后，須對拱塔間的夾角、拱平面外的變形進行精確定位調整后[13]，才可實施拱腳焊接，與拱座形成整體；3) 拉索安裝順序為先水平索，后斜拉索[14]，注意采取有效措施保證水平索低應力下錨固的可靠性[15]。

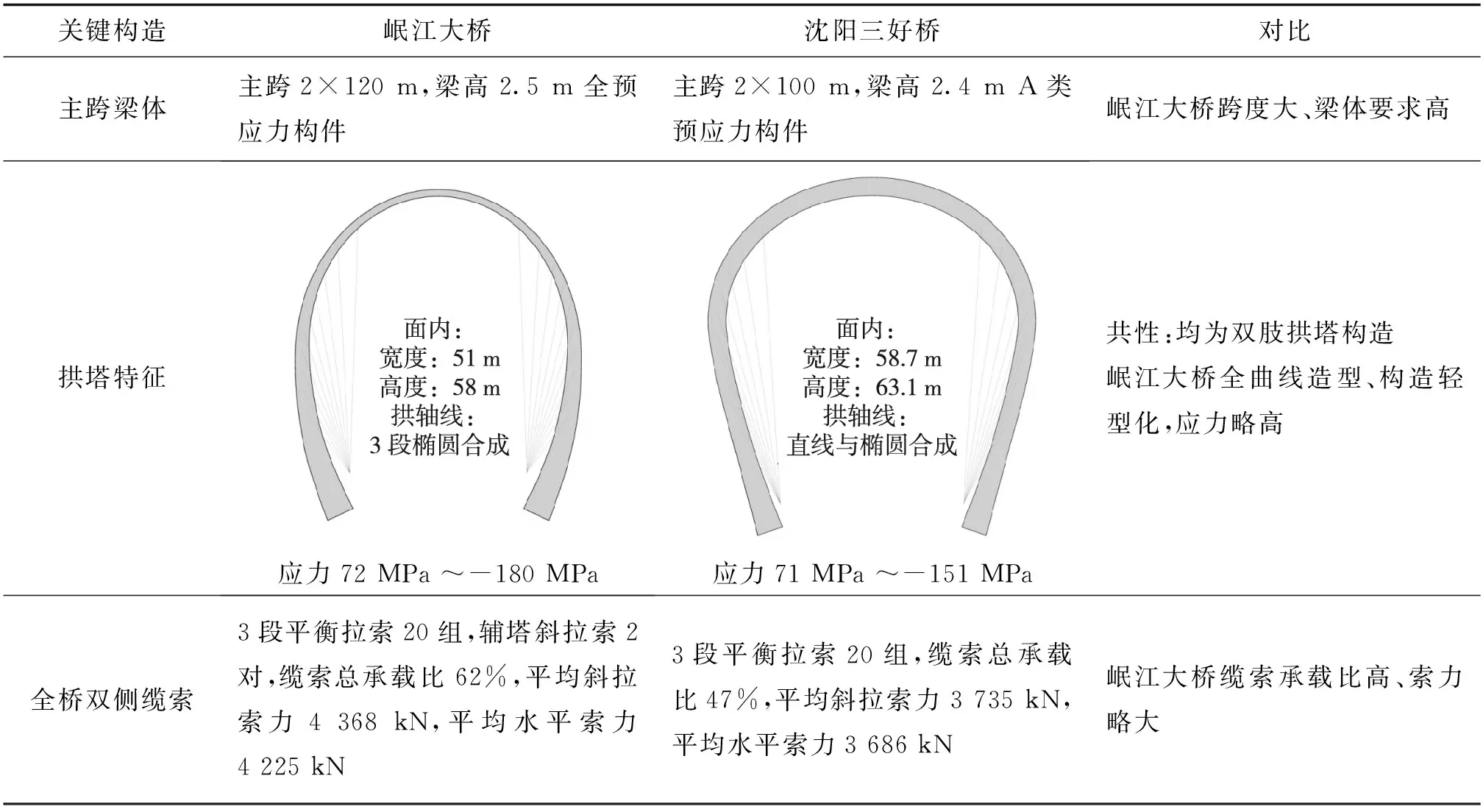
表2 岷江大橋與沈陽三好橋關鍵構造對比

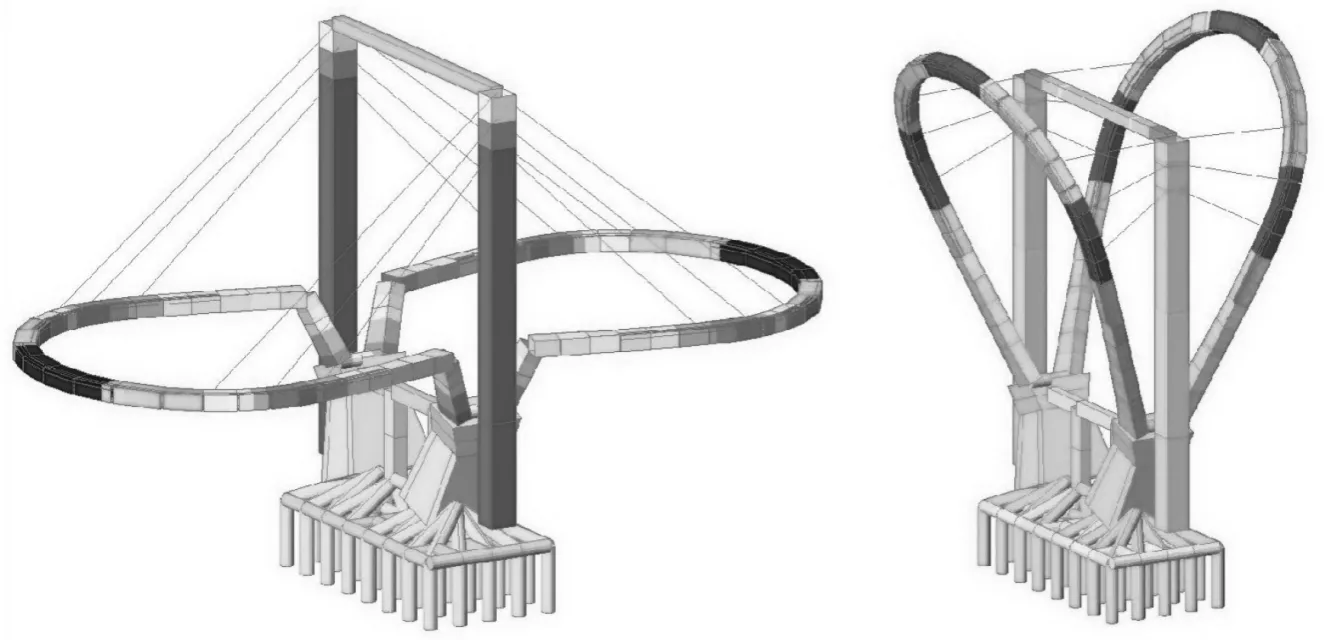
(a) 有限元分析模型

(b) BIM分析模型

5 結束語

1) 纜索對索輔梁橋跨度有提升作用，隨著纜索承載比的增加而增長；對于混凝土梁體，采用斜拉索對跨度的提升作用更為有效，比垂直吊索高出 30%～60%；采用承載比約60%的斜拉索輔助，可滿足岷江大橋120 m的跨度要求。

3) 雙肢鋼拱塔間夾角是重要的設計參數，對拱塔受力影響顯著，夾角在39°～48°區間為合理的角度值；岷江大橋取值約為44°時拱塔受力最小，可實現運用“3段平衡式拉索”達到梁體和鋼拱塔受力最佳的設計目的。

4) 輔塔設置斜拉索對邊跨梁體受力改善明顯，以控制邊跨梁體滿足全預應力構件為目標，應在輔塔設置一定數量的斜拉索，對岷江大橋建議采用2對斜拉索輔助邊跨受力。

5) 對眉山岷江大橋進行優化的結果表明，基于索輔梁橋設計的鋼拱塔斜拉橋體系可靠，3段平衡式拉索與輔塔斜拉索組合使各構造協同受力，充分發揮各自的承載能力，同步對稱豎轉施工能保證拱塔施工中的安全性，是可靠的工法，建議采用。