基于SAPSO-BP的薄壁件側銑加工變形預測方法研究*

鄭華林 馮 博 張世貴 張晟瑋 李 湉

(①西南石油大學機電工程學院，四川 成都 610500；②中國航發航空科技股份有限公司，四川 成都 610500)

薄壁零件廣泛運用于航空航天、汽車等領域，其加工精度要求愈來愈高。在其實際側銑加工過程中，由于薄壁件的弱剛性，極易產生“讓刀”現象，造成復雜的變形，嚴重影響了零件的加工質量。因此，提升薄壁件加工變形預測的準確性，對于提高相關薄壁件的加工精度具有重要的意義。

近年來，許多學者在薄壁件加工變形預測領域進行了大量研究。部分學者[1-2]利用有限元方法實現了薄壁件加工的變形預測；Zhang等[3]通過神經網絡建立薄壁件切削參數與變形的非線性關系，提升了預測效率與預測精度。秦國華等[4]通過有限元方法獲取樣本，利用BP神經網絡建立了刀具的幾何參數和薄壁件加工變形之間的非線性映射關系。然而已有研究中，若只使用有限元方法，當加工參數改變時，模型需重新計算預測效率低；利用神經網絡預測的相關研究中通常選用傳統的神經網絡，很容易出現陷入局部最優和收斂慢的問題，導致預測精度較低；同時在側銑加工中，薄壁件因“讓刀”現象，在不同高度位置處的變形是不一致的，相比于其他位置，隨著薄壁高度位置的增加薄壁件變形越大，薄壁件的加工質量也越難控制[5]，因此壁高也是薄壁件變形預測中需要考慮的重要影響因素。

針對上述問題，提出了一種基于SAPSO-BP神經網絡技術預測薄壁件側銑加工變形的方法。以T型薄壁件為例，通過仿真軟件，建立了T型薄壁件側銑加工仿真模型，并通過實驗驗證了其有效性，為后續神經網絡提供訓練樣本；通過引入模擬退火粒子群算法(SAPSO)，優化BP神經網絡的初始權值與閾值，建立以銑削參數、薄壁件空間高度為輸入，薄壁件變形量為輸出的SAPSO-BP薄壁件側銑加工變形預測模型，并驗證分析了其可行性。

1 薄壁件側銑加工的有限元仿真模型

1.1 薄壁件側銑加工變形的有限元預測模型建立

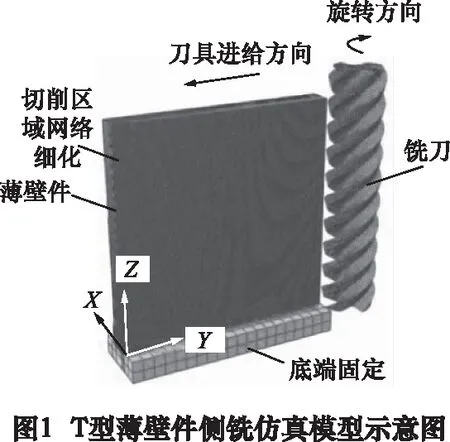
利用有限元仿真方法對薄壁件側銑加工進行合理的建模和分析，能獲取薄壁件側銑過程中的具體變形情況。如圖1所示為基于有限元仿真軟件ABAQUS建立的T型薄壁件側銑加工示意圖。為滿足薄壁特征[5]，薄壁長L=40 mm,寬B=40 mm，厚H=3 mm。加工采用螺旋角β=60°，前角γ=3°，后角α=8°的四齒圓柱立銑刀，工件采用鋁合金7075-T6，刀具采用硬質合金YG8。在對鋁合金7075-T6薄壁件的銑削仿真分析中，為保證仿真的準確性，選用廣泛運用于切削領域的Johnson-Cook本構模型與Johnson-Cook失效模型，具體參數參考文獻[6]設定。

1.2 有限元仿真模型驗證

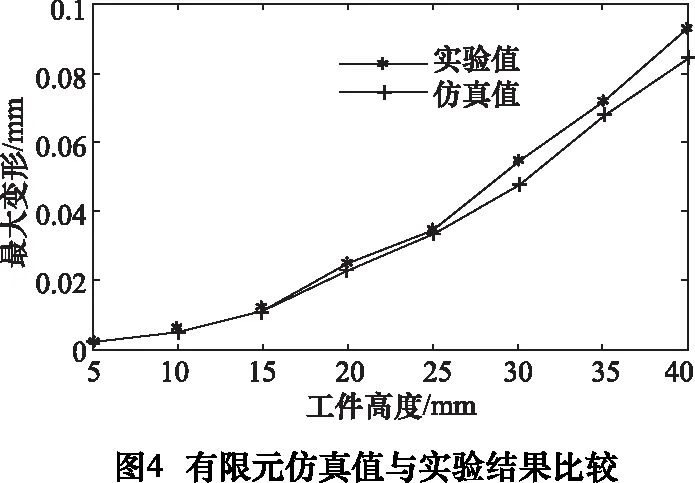
為驗證有限元仿真模型的有效性，進行了薄壁件側銑驗證實驗。如圖2所示，實驗在VMC850三軸加工中心上進行，工件尺寸和刀具的選擇等各方面與有限元仿真模型一致，加工參數選擇徑向銑削寬度ae=0.2 mm,軸向銑削深度ap=40 mm，主軸轉速n=2 000 r/min，每齒進給量f=0.025 mm/z，進刀方式為順銑。如圖1所示，沿Z軸正向，以步長為5 mm，利用Daisy686三坐標測量儀獲取薄壁件在每個高度上的最大變形，圖3為測量過程。并將實驗結果與相應的仿真結果進行對比如圖4所示，通過對比分析后可知，兩者變形趨勢一致，仿真結果與實驗結果吻合度較高，各點的平均誤差約為9.24%，最大誤差低于14%，說明該有限元模型能有效地反映薄壁件實際的側銑加工變形情況。

2 基于SAPSO-BP薄壁件側銑變形預測方法

2.1 模擬退火粒子群算法

由第一節可知，有限元方法能有效預測薄壁件側銑加工的變形情況，但是當加工參數改變時，有限元模型需重新計算，預測效率低。為此利用BP神經網絡對薄壁件側銑加工變形進行預測，以提升預測效率.但是BP神經網絡在訓練過程中經常因為初始權值和閾值的選擇不當，出現易陷入局部最優、收斂性差和泛化能力較低等問題[7]從而導致預測精度不高.為此,引入了由傳統粒子群算法(PSO)與模擬退火算法(SA)衍生而來的模擬退火粒子群算法(SAPSO)，該算法收斂速率快、魯棒性高，具有較好的全局搜索能力[8]，同時在尋優迭代過程中，通過具有概率跳脫特性的Metropolis判定準則[9]，使其在一定概率上接受“惡化解”，在高溫時有著更大的搜索空間，當溫度降低時，不合理粒子的數量與擾動大幅降低[10]，在不影響優化結果準確性的前提下，能有效地避免局部最優的問題。

為得到適應性較好的初始權值和閾值，利用SAPSO算法對BP神經網絡的初始權值和閾值進行迭代優化，進而提升BP神經網絡對薄壁件側銑加工變形的預測精度。

2.2 模擬退火粒子群算法優化神經網絡

BP神經網絡由輸入層、隱藏層和輸出層3部分組成，為揭示在不同加工參數下，薄壁件不同空間高度位置處的變形情況，建立了BP神經網絡薄壁件側銑加工變形預測模型，相比于傳統只以銑削參數為輸入的神經網絡預測模型，增加薄壁件的空間高度作為神經網絡的輸入。其輸入層神經單元包括：主軸轉速、每齒進給量、軸向切深、徑向切寬和薄壁件空間高度共5個輸入，輸出層神經單元為相應銑削參數下對應薄壁件空間高度處在側銑加工中因讓刀產生的最大變形。如此便可通過輸入不同銑削參數與薄壁件高度信息，得到對應銑削參數下薄壁件不同高度位置處的最大變形。

隱藏層是神經網絡的重要組成結構，隱藏層的神經元個數由式(1)可知[7]，神經元個數在4～14，經多次測試，隱藏層神經元的個數選擇為12；設置神經網絡訓練誤差目標為5×10-4，學習效率為0.05，迭代次數為1 000，以此完成BP神經網絡薄壁件側銑加工變形預測模型的構建。

(1)

式中：n1、n、m分別為隱藏層、輸入層和輸出層神經元個數；a是隨機數，介于1～10。

針對所建立的BP神經網絡薄壁件側銑加工變形預測模型，利用SAPSO算法對其進行優化，其具體實現流程如下：

第一步：確定神經網絡結構，初始化算法種群參數與粒子的速度與位置。如式(2)所示，將預測值與目標值的誤差絕對值之和f設置為SAPSO優化算法的適應度函數。通過適應度函數計算各粒子的最優適應度值，進而找到當前最優種群位置。

(2)

式中：ti為目標值；yi為預測值；abs為取絕對值。

第二步：根據初始種群對應的最大適應度值fmax和最小適應度值fmin，計算初始溫度T0=fmax-fmin，溫度下限Tmin=T0×10-3，并設定溫度變化系數a取值為[0.8，0.999 9]。

(3)

j=(1,2，…,N)

(4)

式中：T表示當前的溫度。

第四步：根據溫度變化系數，更新當前溫度Tk=aT0，若未達到終止條件或Tk>Tmin,則循環繼續實施3～4步驟流程，否則退出循環輸出最優種群位置。

第五步：通過優化后所得出的參數，即權值與閾值，帶入BP神經網絡中，進行訓練和預測。

其中SAPSO算法中一系列參數設置如下：粒子種群數選擇20；ω表示慣性權重取值為0.729；最大允許迭代次數為100，加速因子c1=c2=1.494 45，粒子速度vmax=1、vmin=-1；溫度變化系數a的取值范圍[0.8，0.999 9]，取a=0.9；以此構建相應的SAPSO-BP神經網絡薄壁件側銑加工變形預測模型。

2.3 神經網絡訓練樣本的獲取

為滿足神經網絡訓練樣本遍歷性、相容性和致密性的要求，薄壁件側銑加工銑削參數選擇如下：主軸轉速選擇1 500～4 500 r/min；每齒進給量選擇0.05～0.1 mm/z；軸向切深選擇0～40 mm；徑向切寬選擇0.2～0.6 mm。薄壁件的空間高度位置選擇范圍為0～40 mm。

同時，神經網絡預測模型需要大量的訓練樣本，若通過實驗獲取將會產生極大的實驗成本，為減少實驗成本，樣本通過第一節中已驗證過的有限元仿真方法獲取，整個樣本共540組數據，部分樣本數據如表1所示；將樣本分別帶入所構建的SAPSO-BP與BP神經網絡中進行訓練，完成相應神經網絡變形預測模型的建立。

表1 部分樣本數據

3 算例驗證

為驗證所提預測方法的預測準確性，利用所建立的SAPSO-BP與BP神經網絡變形預測模型分別對1.2節中通過實驗直接驗證的加工參數下各高度位置處的最大變形進行預測，高度位置的選取與1.2節一致。SAPSO-BP神經網絡模型和BP神經網絡模型的預測值與仿真值對比圖如圖5所示，二者的預測相對誤差如圖6所示，結果誤差對比如表2所示。通過圖5可得SAPSO-BP與BP神經網絡預測的薄壁件在其高度方向上的變形趨勢與仿真大體一致，但是SAPSO-BP神經網絡的預測值更接近仿真值；通過圖6可知，在各高度位置處SAPSO-BP神經網絡的預測精度普遍要高于BP神經網絡，同時通過表2的誤差對比，SAPSO-BP神經網絡的平均相對誤差比BP神經網絡低約5%，說明通過模擬退火粒子群優化后的BP神經網絡，在預測精度和預測穩定性上都有著一定的提升，能更有效地反映薄壁件的側銑加工變形情況。同時如圖5所示，相較于其他相關的神經網絡預測模型[4，7，11]在確定的銑削參數下只能輸出其整體最大變形或平均變形的情況，該神經網絡預測模型能較為詳細地反映薄壁件不同高度位置處具體的變形大小與變形趨勢。

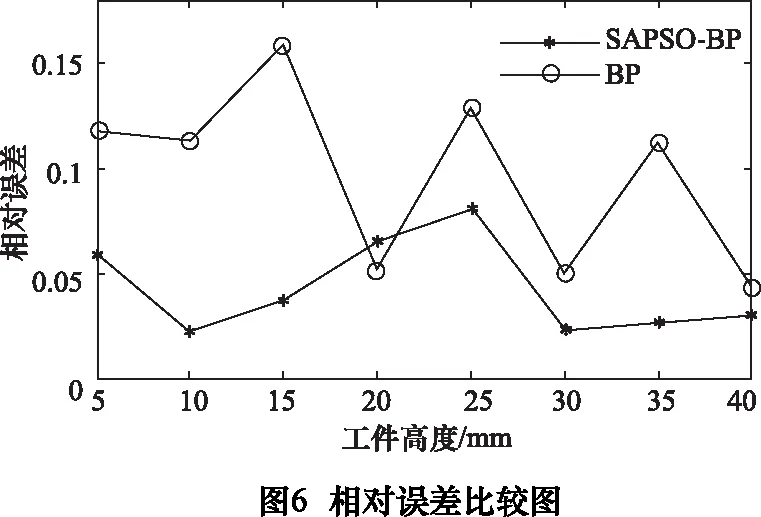
表2 結果誤差對比

4 結語

本文以T型薄壁件為例，建立了薄壁件側銑加工的有限元仿真模型并通過實驗驗證了其有效性，為后續神經網絡訓練提供樣本；利用SAPSO-BP神經網絡，構建了銑削參數、薄壁高度和薄壁件加工變形之間的非線性關系，建立了薄壁件側銑加工變形預測模型，為其他類似薄壁件的加工變形預測提供了借鑒，并得出以下結論：

(1)與BP神經網絡相比，所建立的SAPSO-BP神經網絡預測模型，對薄壁件的變形預測更為準確，預測結果也更加穩定。

(2)建立的SAPSO-BP神經網絡預測模型，相比于傳統的神經網絡預測模型，可以較為有效反映薄壁件在高度方向上的變形趨勢與大小，為后續薄壁件變形控制研究提供較為詳細的數據依據，提升薄壁件變形控制效果。