基于改進粒子群算法的工業機器人軌跡規劃*

韓順杰 單新超 于愛君 符金鑫

(①長春工業大學電氣與電子工程學院，吉林 長春 130000；②北京首鋼國際工程技術有限公司，北京 100043)

隨著智能化制造在社會發展中的地位越來越重要，機器人成為智能化發展過程中不可或缺的關鍵因素，如何讓機器人更加智能、安全、可靠地運行顯得尤為重要[1-2]。軌跡規劃是機器人技術中的重要組成部分，也是一直以來機器人運動學中研究的熱點問題。軌跡優化能進一步改善規劃軌跡的性能，滿足實際需求，縮短機械臂運動時間，減少能量消耗，同時能夠避免不必要的抖動及沖擊，增加平穩性[3-4]。

國內外學者對軌跡規劃的相關研究論文已有很多，文獻[5-6]采用三次多項式函數進行軌跡規劃，結構簡單，易于實現，但其二階導數不連續導致機械手運行不穩定；文獻[7]提出了5-7-5次分段多項式與復合型法相結合的方式，提高了效率，降低了能耗，但運算相對復雜，高階次更容易引起“龍格”效應的產生；文獻[8]以抑制機械振動為目標，將遺傳算法與多項式軌跡規劃相結合；文獻[9]采用權重系數法構成目標函數，并采用粒子群算法對五自由度機械臂進行運動規劃。以上研究雖然解決了傳統算法難以優化高次多項式的問題，但并未考慮智能算法的收斂速率以及陷入局部最優的問題。

本文以三菱RV-4FL-D機械手為研究對象，以機器人運動空間的軌跡和分揀作業的實際工況提出了4-3-4多項式函數對機械手進行運動軌跡規劃，使其計算過程簡單，各關節的位置、速度、加速度連續可控。標準的粒子群算法存在前期收斂速度慢，后期容易陷入局部最優等問題，本文采用改進的粒子群算法，將標準粒子群中的學習因子由定值改變為可以根據環境動態調節的變量，改進后的粒子群算法前期可以快速收斂，后期可以準確收斂到最優解。實驗證明，將4-3-4多項式函數與改進的粒子群算法相結合的軌跡規劃方法有效提高了求解的速度與精度，并且保證了效率與穩定性的綜合最優。

1 多項插值函數的構造

為了保證機械手在軌跡規劃中的穩定性，其位移、速度、加速度隨時間的變化曲線都應是連續可控的，常用的高次多項式函數為3次、5次、7次多項式，則分別需要對運動位置施加至少4個、6個或8個約束條件[10]。3 次多項式插值是關節空間中最基本的插補方法，3次多項式插值能夠保證位移和速度連續，但未使用加速度約束，所以不能保證加速度連續，可能會導致關節加速度突變產生沖擊。5次多項式能使加速度連續光滑，但加加速度存在明顯突變。7次多項式雖然可以保證加加速度連續，但高階次會導致凸包性過差，并且計算量過大。

為了使機械手在作業中保證運動軌跡整體連續并增加效率，根據實際工況需要，將機械手的工作區間分為三段，采用4-3-4多項式插值函數，其中在第一、第三階段采用4次多項式進行插值，第二階段采用3次多項式插值。

4-3-4多項式插值位移函數為：

(1)

式中：i=1,2,3，…,n,n為關節數，q1i、q2i、q3i為第i個關節對應的第一、第二、第三區間的位置。其約束條件分別為初始位置、速度、加速度，路徑點1、2的位置，路徑點的位置、速度和加速度保持連續，終點的位置、速度和加速度共14個。式(1)中所有的系數可以由上述的約束求出，如式(2)～(4)所示：

(2)

q=[q10 0q2q20 0q3

q30 0q40 0]T

(3)

(4)

式中：

2 改進的PSO算法

在關節空間中采用4-3-4多項式函數進行機械手運動軌跡規劃，可以得到機械手在各段端點處的位置、速度、加速度的運動軌跡連續并且可控。但由于在構造分段多項式函數的各工作區間的時間間隔ti1、ti2和ti3是提前預設的，沒有對任意時刻的運動學參數進行約束，所以不能保證機械手整體的運動平穩、減小沖擊。傳統的優化方法對于高次多項式而言并不適用，需要采用智能算法對適應函數進行優化。本文在使優化目標滿足運動學約束的基礎上，采用改進的優化算法，在完成指定任務的基礎上增加機械手的效率和平穩性。

2.1 運動學約束與適應度函數

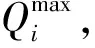
(5)

本文優化的目的是使機械手在完成任務的基礎上增加效率和穩定性，所以將運行時間最短作為適應度函數，即：

f(t)=min(ti1+ti2+ti3)

(6)

2.2 改進的PSO優化算法

在標準的PSO優化算法中，粒子的特征用位置、速度和適應度值來表示，速度代表了粒子在不斷迭代中發生的位移，適應度值判定解的質量。在粒子向更優的特征不斷迭代中，個體極值和全局極值也在不斷更新，更新公式如下：

(7)

(8)

式中：xid為粒子位置，i代表的是粒子群中的一個任意粒子，d代表維度；vid代表上述粒子在相應位置處的速度；pid表示的是上述粒子在該條件下個體的最優位置；pgd是當前條件下全局最優位置。ω為慣性權重；非負常數c1、c2為學習因子,r1和r2為[0,1]上均勻分布的隨機數。

標準PSO算法運算簡單、高效且搜索速率高，但易陷入局部最優[11]。根據式(7)可知，當c1=0時，剩余為社會認知部分，收斂速度較快，但容易陷入局部最優；當c2=0時，剩余為個體認知部分，收斂速度較慢。為了更高效地獲得全局最優解，本文采用一種動態的方式給c1和c2賦值，在搜索初期，個體信息的意義大于全局信息，所以c1的取值大于c2，搜索后期為了讓更加快速準確地收斂于全局最優，c2的取值大于c1的取值，構造的函數如下：

(9)

式中：t為當前迭代次數，Tmax是最大迭代次數。

改進的粒子群算法對機械手關節i進行軌跡優化的步驟如下：

(1)將由m個粒子組成的種群初始化，以隨機的方式得到粒子的速度和位置。

(2)將m個粒子的參數代入式(2)～(4)，求出14個參數aij代入式(1)并對其求導，將得到的當前速度與約束進行比較，如滿足約束，則根據適應度值判斷粒子的優劣；如不滿足約束，在選擇最優粒子時會將該粒子排除，并且未滿足約束的粒子在不斷迭代過程中會逐漸向最優值前進，直到滿足約束。

(3)找出每一個粒子自身到目前為止搜尋到的最優位置作為Pd;找出所有粒子當前的最優位置，作為Gd。

(4)根據式(7)、(8)更新粒子的速度和位置，重新構成具有新的位置和速度的m個粒子組成的種群。

(5)如滿足迭代終止條件，則計算結束，得出最優適應度值，否則返回步驟(2)。

設定初始粒子數M=50，初始位置為0～1 s隨機位置，飛行速度為[-2，2]，慣性權重ω=0.6，r1、r2為[0,1]上的隨機數，迭代次數為50。

3 建模仿真實驗

本文以三菱RV-4FL-D機器人為研究對象，實驗平臺如圖1所示。采用標準D-H法建立運動學坐標系模型：以機械手各關節旋轉軸軸線方向為坐標zi向，軸zi與zi-1的公垂線方向為xi向，yi通過右手定則確定[12]。依據該方法其具體坐標系如圖2，得到的D-H參數如表1。

表1中αi表示扭曲度，ai表示桿件長度，di表示桿件偏移量，其中L1=170 mm，L2=280 mm，L3=60 mm，L4=350 mm。應用MATLAB仿真軟件內Robotics Toolbox工具箱對其建模[13-14]，如圖3所示。

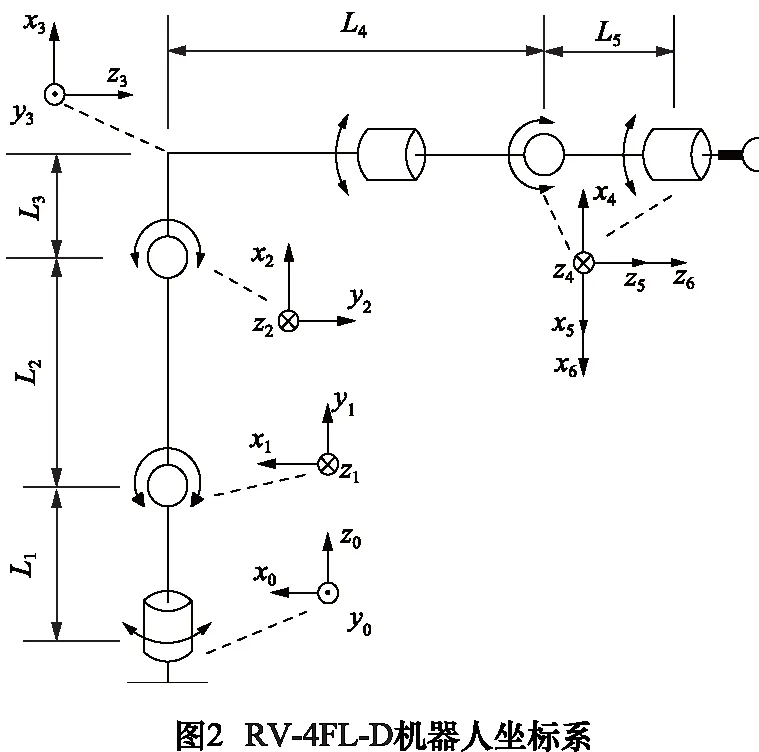
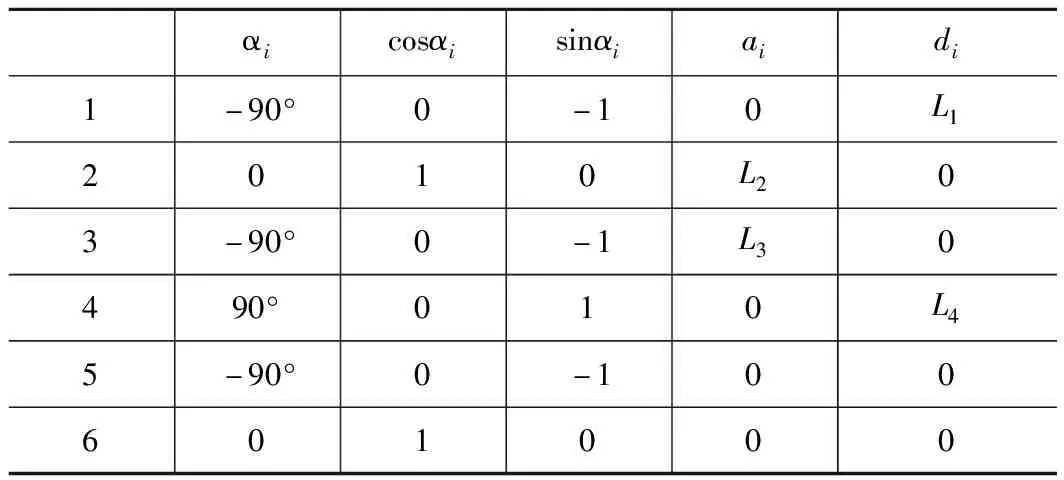
表1 RV-4FL-D機器人D-H參數

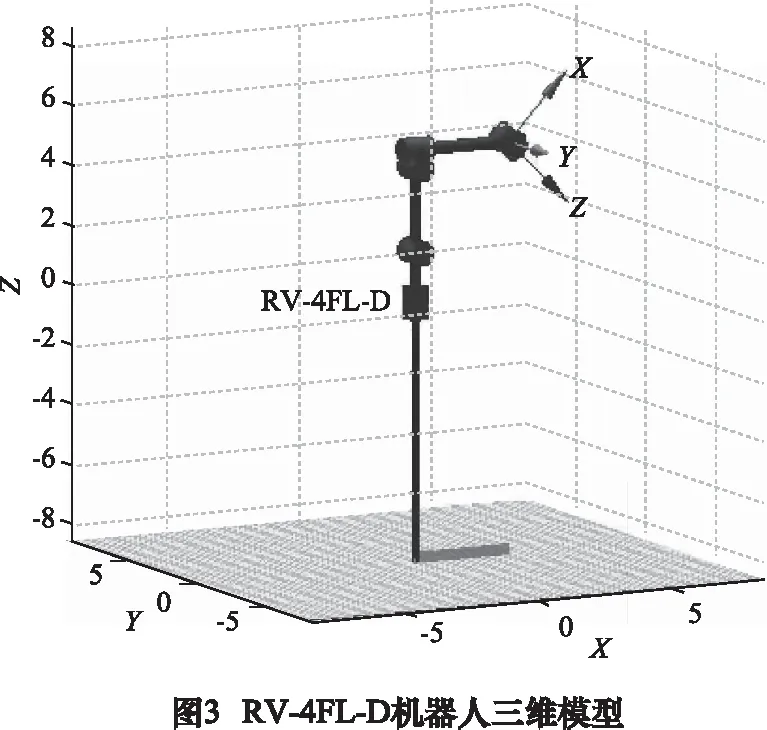
在笛卡爾坐標系下給定機械手的初始位置、路徑點1的位置、路徑點2的位置、終點位置，見表2。

表2 笛卡爾空間路徑

通過逆運動學，將初始點、路徑點、終點由笛卡爾空間表示方式轉化為關節空間表示方式，如表3。

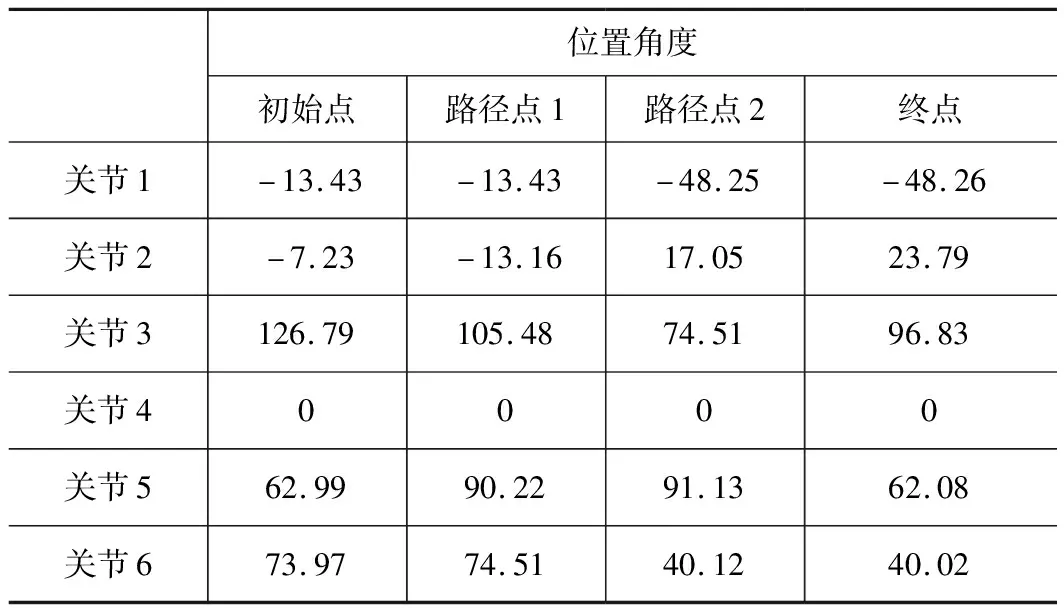
表3 各關節的關節空間差值點

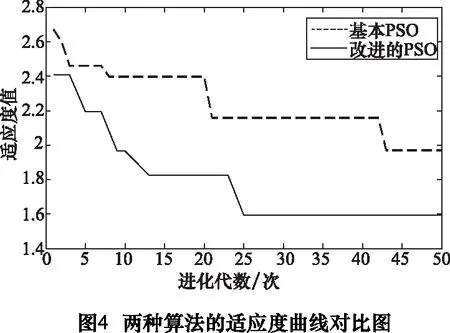
基本PSO算法的最優粒子適應度曲線與改進的PSO的適應度曲線對比如圖4所示。

由圖4可看出，改進后的PSO算法在前期的收斂速度更快，且適應度值小于基本PSO算法約20%，由此可見改進后的算法效果更優。

采用改進的PSO算法對4-3-4分段多項式函數進行以時間為目標的優化，關節1的最優粒子位置迭代過程如下：

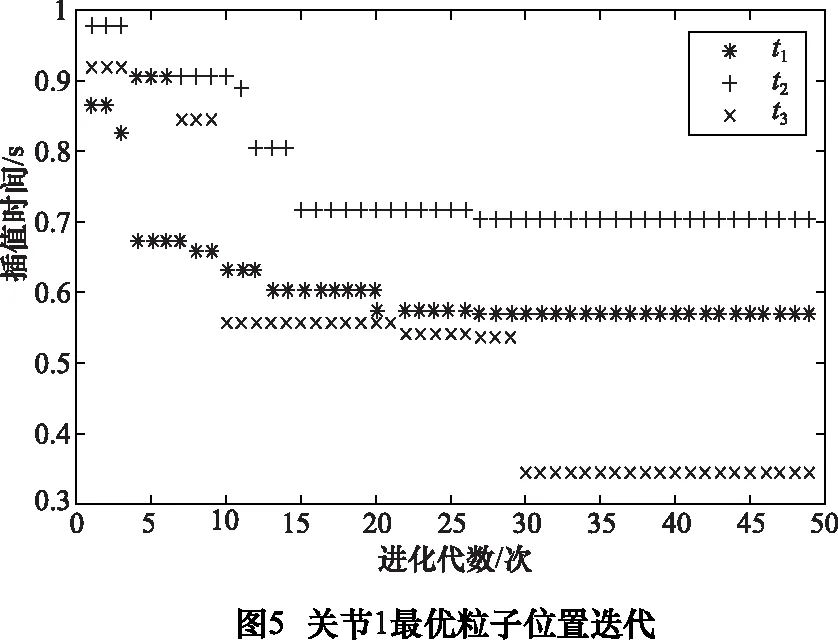
對于其他關節也同樣采用上述方法進行尋優，從而得到各個關節的運行最優時間，如表4。

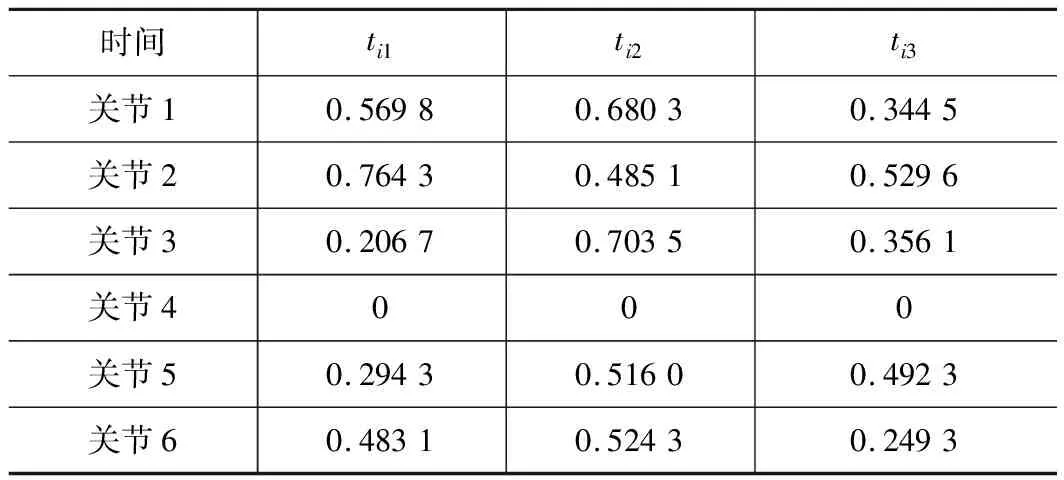
表4 各關節優化結果

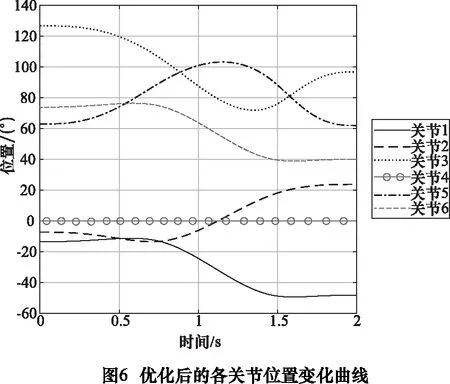
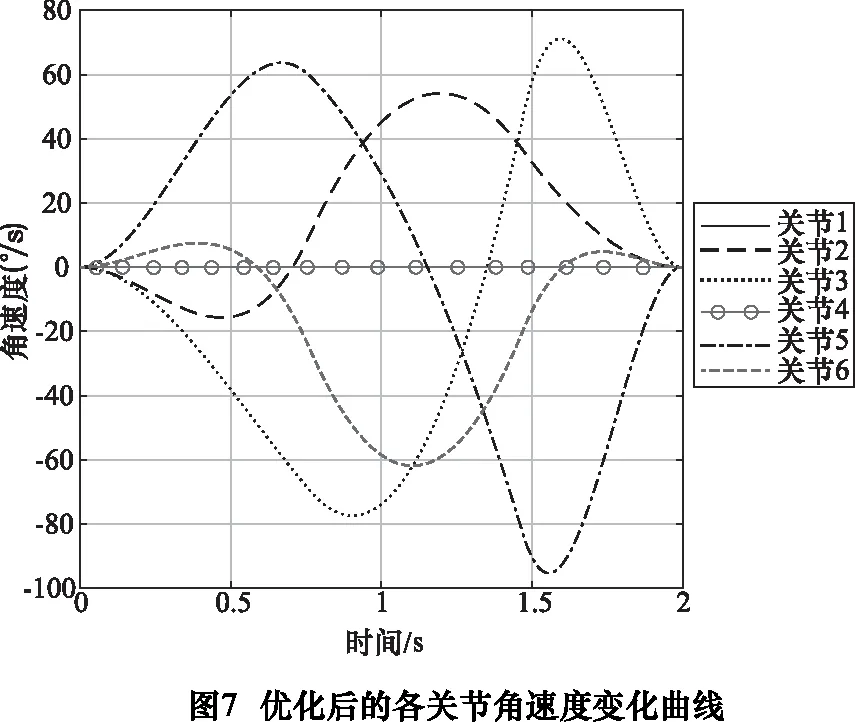
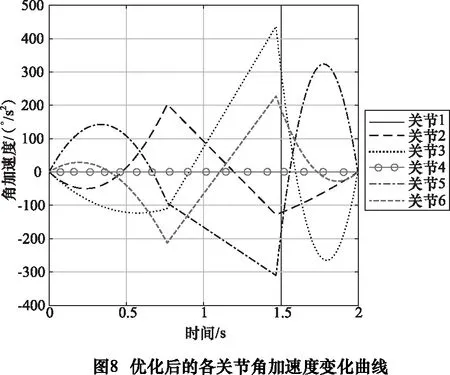
為了保證機械手的各個關節以相同的時間到達目標位置，因此選用所有關節的各段插值時間的最大值，機械手運行時間為T=1.997 4 s。關節1～6的位置、速度和加速度運動軌跡變化曲線分別如圖6～8所示。

由以上仿真結果分析可得，采用改進后的軌跡規劃方法能夠縮短整個機械臂的運行時間，并且保證規劃出來的位移、速度、加速度曲線在整個運動過程中的連續性在一個較理想的范圍內，從而使得在縮短時間的前提下還能繼續保證整個機械臂的穩定運行。

4 結語

本文提出的軌跡優化方法綜合考慮了機械手的效率和平穩性指標，提出了4-3-4次多項式插值進行擬合，大幅減少計算的同時，還保證了機械手運行中的位置、速度、加速度連續可控，解決了文獻[5-6]加速度不連續帶來的沖擊和文獻[7]計算復雜，易產生“龍格”現象的問題。相較于采用遺傳算法[8]和基本粒子群算法[9]，改進的PSO算法有效地解決了高次多項式難以用傳統方法優化的問題，動態調節的學習因子可以快速準確地收斂到最優解。結果表明，采用4-3-4分段多項式進行軌跡規劃結合改進的PSO算法對機械手運動軌跡進行優化，軌跡運行時間較只進行多項式軌跡規劃縮短了約40%，較基本PSO軌跡優化縮短了約20%，各關節運行過程平穩，達到了預期的優化目標。