直弧形板坯連鑄機彎曲應變分析

黎建全，何 博，龍木軍

(1.攀鋼集團攀枝花鋼釩有限公司提釩煉鋼廠，四川 攀枝花 617062；2. 中國重型機械研究院股份公司，陜西 西安 710032；3.重慶大學材料科學與工程學院，重慶 400044)

0 前言

對于直弧形連鑄機而言，直線段有利于鋼液中夾雜物的上浮，可以生產質量和性能要求更高的鋼種；而彎曲段將迫使鑄坯由垂直彎曲成弧形，并使得連鑄坯產生較大應力應變[1-3]；此時，如果彎曲區域夾持輥列的工藝和設備設計不合理，將對鑄坯的質量產生有害的影響[4-9]。一般而言，二冷彎曲段的彎曲工藝和設備參數設計的合理性對鑄坯的中間裂紋的產生有著密切關聯[10-12]。針對某鋼廠2號板坯連鑄機在生產某些鋼種時，存在較為嚴重的中間裂紋缺陷的問題，分析認為除了鋼種本身的高溫凝固行為影響外，連鑄機二冷彎曲段設備和工藝參數設計的合理性至關重要[13-22]。為此，該研究擬運用彎曲變形的理論計算和應用彈塑性模型(MSC.MARC軟件)的應力應變仿真兩個方面對某廠2號板坯連鑄機彎曲段的輥子排布在不同鋼種和拉速下的合理性進行分析評價，進而對生產實踐提供相關指導。

1 2號板坯鑄機彎曲段的主要參數

某廠2號板坯連鑄機為二冷區帶直線段的直弧形連鑄機,設計年產合格鑄坯100萬噸，足輥段和二冷彎曲段上部為直線區，二冷彎曲段下部為彎曲區,鑄坯在彎曲段從垂直逐漸彎曲到鑄機的主半徑。連鑄機主要工藝參數見表1，彎曲段的幾何參數如圖1所示,彎曲段詳細參數見表2。

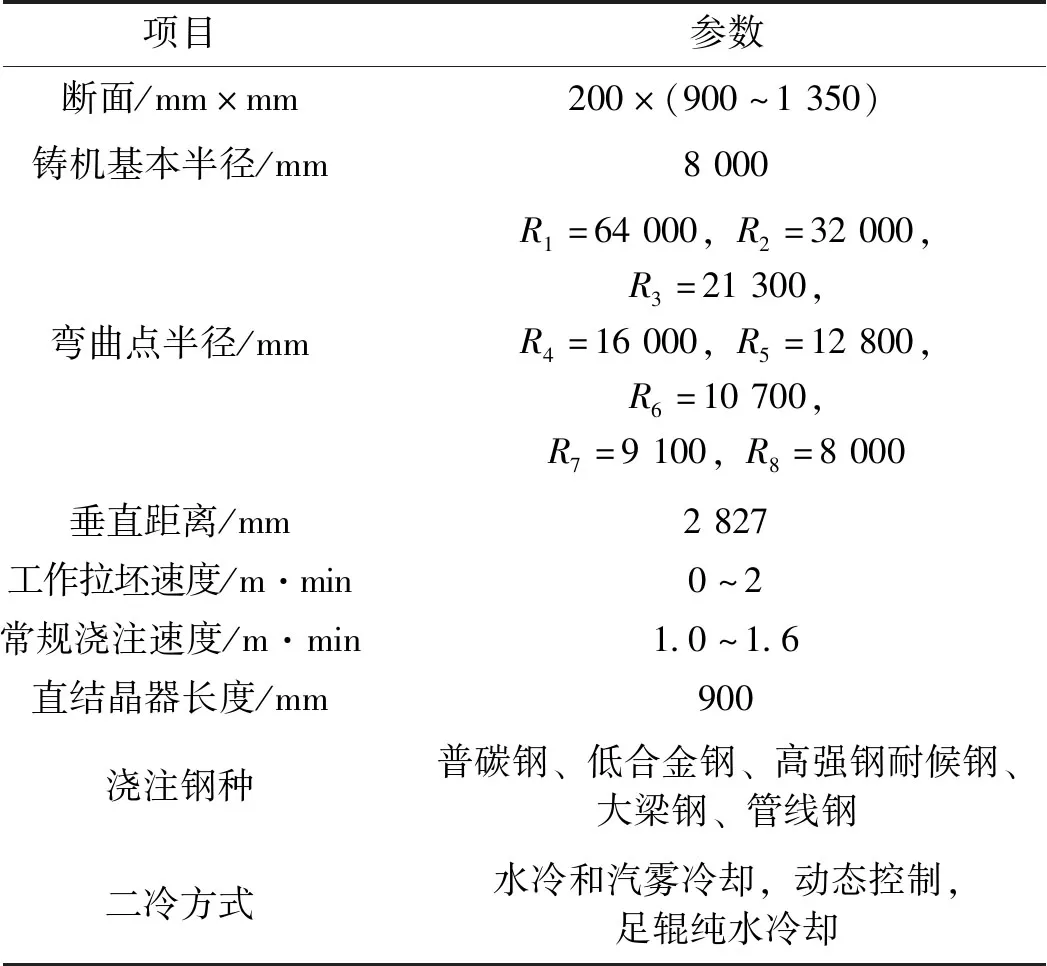
表1 多點彎曲多點矯直,單流直弧形連鑄機參數

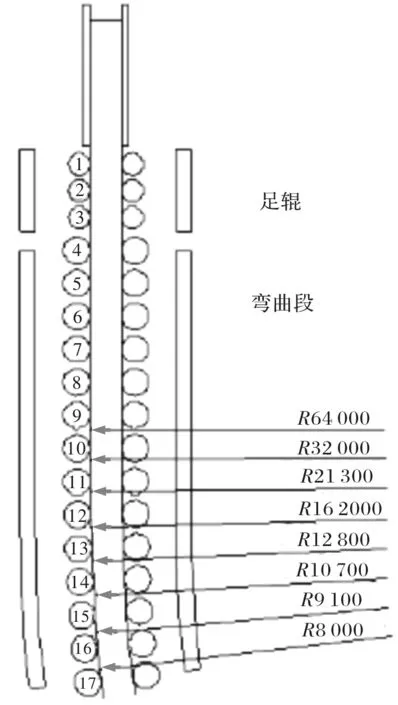
圖1 板坯連鑄機彎曲段結構示意圖

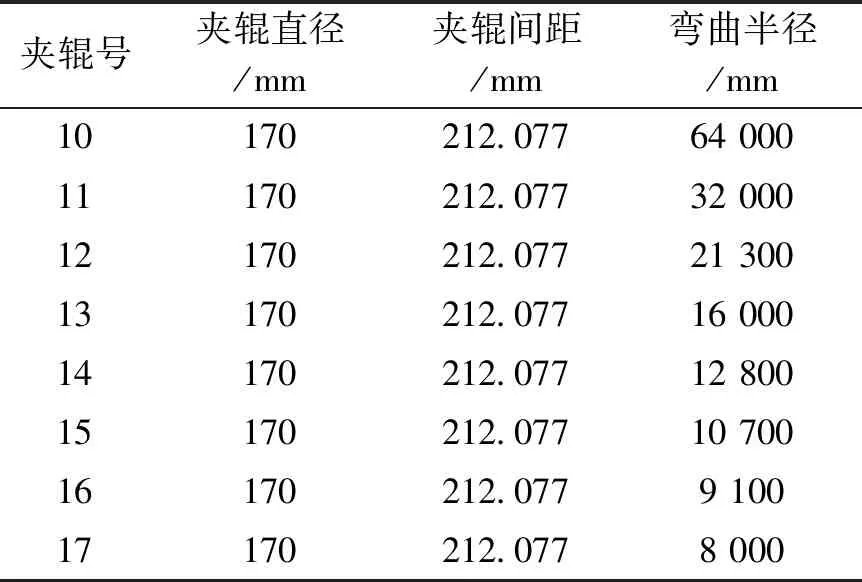
表2 連鑄機彎曲段參數

2 彎曲變形率理論計算

連鑄機的彎曲段半徑變化是根據各彎曲點表面變形率相等的原則[11]設計的，即鑄坯外弧側表層金屬的彎曲變形率在各彎曲點都相等。連鑄機各彎曲點彎曲應變6可采用公式[11](1)計算。

(1)

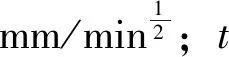
有研究表明[13]：距離鑄坯表面越近，節點受到的等效應力值就越大，鑄坯變形也最大。因此，為研究彎曲區域內各過渡曲率半徑Ri(i=1,2,…,8)是否能滿足鑄機設計要求，各彎曲輥處的鑄坯凝固殼彎曲變形是否在允許范圍內，用外弧側表層金屬的彎曲應變來代替各彎曲點彎曲應變進行計算，將x=D/2代入公式(1)，得到公式(2)，從而計算出從R1到R8各彎曲點的表層金屬變形率[11]。

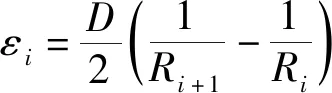
(2)

將各彎曲半徑和鑄坯厚度帶入公式(2)，計算獲得各彎曲點處的表層金屬變形率見表3。

表3 彎曲點表面變形率

由表3可以看出，各彎曲點的外弧側表層金屬變形率幾乎完全相等，也就是說該板坯連鑄機二冷彎曲段中的鑄坯通過8個彎曲輥實現了從垂直方向逐漸被彎曲到8.0 m的主弧形半徑，過渡半徑的設計完全滿足了等變形率原則。

通常情況下，鑄坯兩相界應變值不得超過0.5%[12,14]，而鑄坯表面在彎曲段中受到的應力中，外弧受到最大的彎曲拉應力，內弧受到最大的彎曲壓應力，對稱軸基本在鑄坯的中心；在外弧方向，越往中心拉應力越小。在夾輥與鑄坯接觸的位置附近出現較大的等效應力值[13]。

2號板坯連鑄機彎曲段各彎曲半徑設計，與國內外其它連鑄工程技術公司在相同機型的板坯連鑄機、薄板坯連鑄機對彎曲段輥列的設計是一致。該設計符合等應變速率原則。因此，2號板坯連鑄機二冷彎曲區域的輥列設計(彎曲半徑、外弧輥在空間上的位置)是比較合理的；加上各彎曲輥之間的間距幾乎相同(212.077 mm)，各輥間鑄坯凝固殼所受到的彎曲變形也基本相同。

3 應力應變模型的仿真計算

對各種結構和材料的應力應變仿真分析研究手段，隨著計算機硬件技術和軟件技術的發展，國際上先后開發出了大型通用的有限元結構應力分析軟件如ANSYS、ABAQUS、MSC.MARC等，也還有一些專用有限元應力分析軟件如CAEARII管道應力分析軟件等。其中MSC.MARC軟件是目前應用最多的著名商業軟件之一。

針對2號板坯連鑄機具體情況，運用MSC.MARC仿真軟件,建立從結晶器彎月面到二冷彎曲段的彎曲區域沿拉坯方向上鑄坯的二維彈塑性應力分析模型，對彎曲段鑄坯凝固過程的應力應變進行有限元仿真分析，模擬研究不同鋼種連鑄坯在不同澆注溫度、拉坯速度、冷卻強度工況下，二冷初期彎曲區域應力應變情況。

隨著鋼種、澆注溫度、拉坯速度、冷卻強度的變化，以及連鑄坯受彎曲、拉坯和對弧不準等因素影響，其受到的熱應力和機械應力是復雜多變的。在整個拉坯過程中，鑄坯可能始終或大部分時間都處于超應力極限的受力狀態，此時的鑄坯處于非彈性狀態，屬于非彈性體，因此，在對凝固初期鑄坯的應力進行分析時應采用彈塑性來描述鑄坯的受力狀態。

采用二維應力分析數學模型，計算得到正常冷卻強度和25℃過熱度下不同鋼種(Q235G、P510L、L245MB、Q450NQR1)在不同拉坯速度下(1.0 m/min、1.2 m/min、1.4 m/min、1.6 m/min)的彎曲段的各彎曲輥處鑄坯表層的應變情況，如圖2、圖3所示。

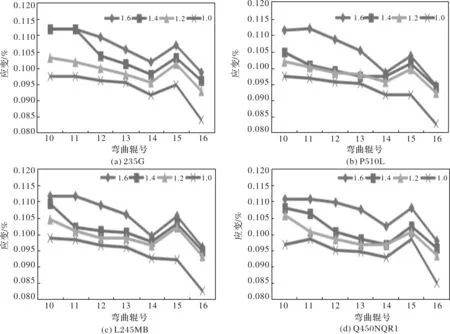
圖2 同鋼種不同拉坯速度下連鑄坯各彎曲點的應變圖

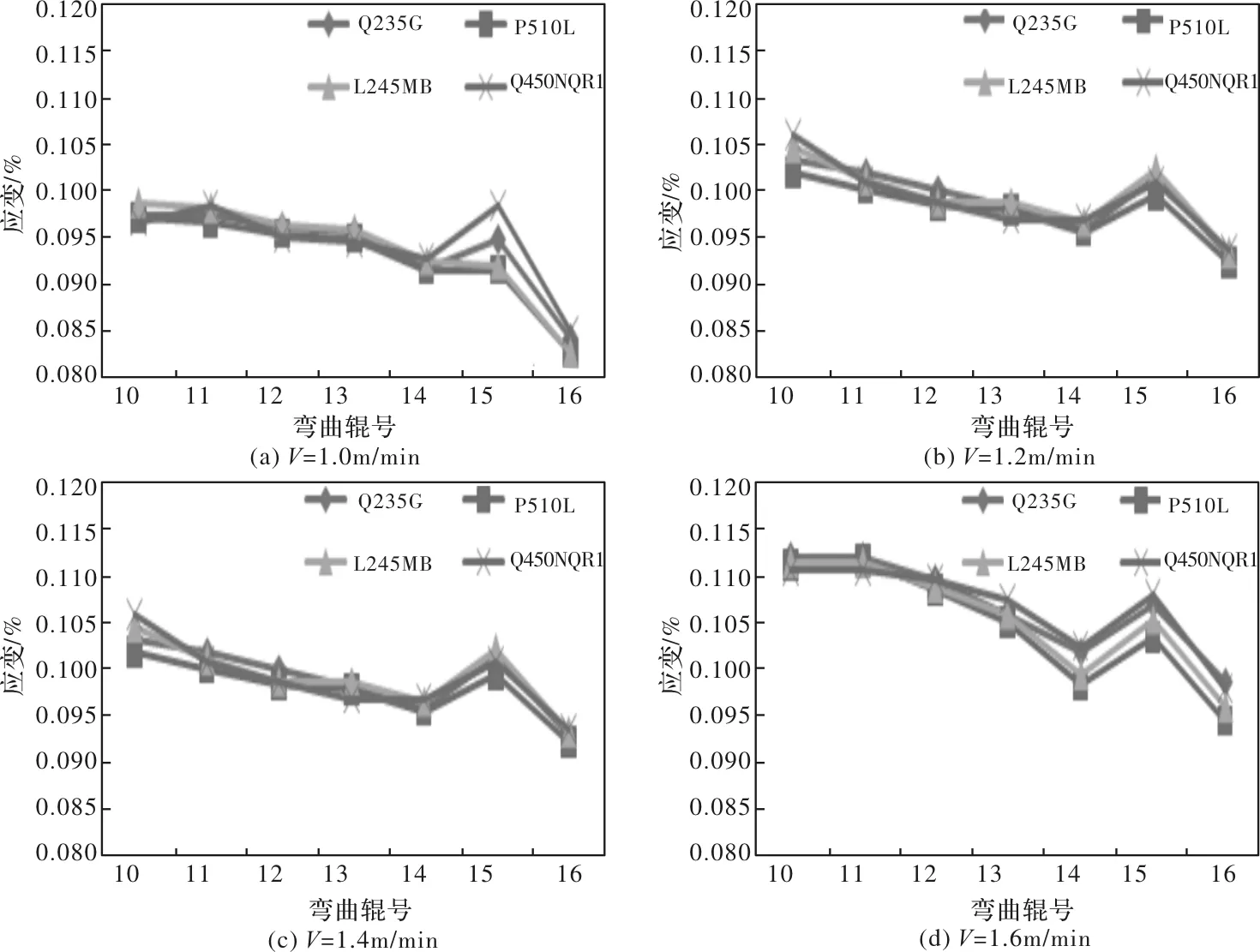
圖3 相同拉坯速度下不同鋼種連鑄坯各彎曲點的應變圖

從圖2中可以看出，同一鋼種, 各彎曲輥處鑄坯表層的應變隨著拉坯速度的提升有所增加。主要是因為在相同冷卻和過熱度條件下，拉坯速度越低，凝固坯殼越厚，抵抗變形的能力也越強。離彎月面越遠時，應變呈現下降趨勢，主要是因為隨著鑄坯的延伸，凝固坯殼越厚抗變形能力越強導致的。

從圖3中可以看出，不同鋼種，各彎曲區域各輥和輥間的應變規律一致，但存在一定差異，這與各個鋼種連鑄坯在高溫下的彈性極限、塑性模量、高溫斷裂強度、屈服強度等鋼種力學性能不同有關。

不同鋼種，計算獲得的表層應力與應變雖有一定的差異，但差異很小。主要是因為彎曲段處于連鑄機頭部，二冷前端，此時二冷初期溫度還很高，坯殼也較薄，因鋼種力學性能不同造成的抗變形能力的差異還體現不明顯，因此計算得到不同鋼種的應變差異也不大。

從圖2、圖3中可以得知，不同鋼種不同拉坯速度情況下，采用彈塑性應力應變模型仿真計算獲得各個彎曲點表層的應變值在0.115%以內，遠低于冶金理論對變形的要求，說明該連鑄機彎曲段輥列設計還是合理的。

模型仿真計算獲得的彎曲區域的應變值較理論計算獲得的應變值要低。分析認為彈塑性應力應變模型仿真計算獲得的結果是表層的應變，考慮了一定的坯殼厚度的影響，而理論計算考慮的是表面的應變，從理論上說表層應變比表面的應變要小。

4 結語

通過采用應變理論計算公式和彈塑性應力應變數值仿真模型計算，2號板坯連鑄鑄機二冷彎曲段的彎曲應變在0.165%以內，各彎曲點表面變形率基本相等，彎曲段的設計能夠實現等彎曲應變的要求。因此，2號板坯連鑄機鑄機彎曲段采用8點彎曲，彎曲半徑依次為R1=64 000 mm，R2=32 000 mm，R3=21 300 mm，R4=16 000 mm，R5=12 800 mm，R6=10 700 mm，R7=9 100 mm，R8=8 000 mm，輥列設計合理。