基于卡爾曼濾波器的分數階PIλDμ控制器

蔡元宵 王蕓芳

(1.寧夏大學新華學院信息與計算機科學系,寧夏銀川 750021;2.陜西汽車控股集團有限公司技術中心,陜西西安 710200)

0 引言

Podlubny在文獻[1]中提出了分數階PIλDμ控制器,其比整數階控制器多了兩個可調參數:積分階次λ和微分階次μ,參數調整范圍增大,能夠更靈活地控制系統。文獻[2]提出了用主導極點法設計分數階PIλDμ控制器。文獻[3]采用幅值裕量法和相位裕量法得出了分數階PIλDμ控制器的參數。針對非線性、參數時變及大范圍攝動系統,結合智能優化算法,文獻[4]提出了用遺傳算法對分數階PIλDμ控制器的參數進行整定。文獻[5]將粒子群優化算法用于分數階PIλDμ控制器的設計。文獻[6]給出了分數階PIλDμ控制器的數字實現方法,為其工程應用提供了可能性。文獻[7]利用控制系統在滿足相位裕度和幅值裕度的魯棒性條件下,設計了對時間常數變化具有魯棒性的分數階PIλDμ控制器。然而,實際系統中的過程噪聲和測量噪聲往往使控制器不能達到理想的控制效果,上述分數階PIλDμ控制器的設計和研究尚未考慮這些干擾噪聲的影響。

卡爾曼濾波器具有遞歸、線性、無偏和方差最小等特點,因此在對機動目標的跟蹤中具有良好的性能,例如在軍事、航天和工業生產的自動控制領域都有廣泛的應用。文獻[8]將模糊控制器的設計與卡爾曼濾波算法融合,提出了一種新的模糊卡爾曼濾波器,在實時性要求很高的控制系統中具有良好的控制性能。文獻[9]將卡爾曼濾波器用于視頻監控系統,對運動目標的適時檢測和跟蹤具有良好的效果。

本文將分數階控制理論和卡爾曼濾波算法進行結合,考慮實際系統中干擾噪聲的影響,設計出基于卡爾曼濾波器的分數階PIλDμ控制器,使系統具有較好的控制性能,且能有效地濾除噪聲。

1 分數階微積分及卡爾曼濾波原理

分數階微積分是指微積分的階次是任意的,分數階微積分常用Grunwald-Letnikov(G-L)定義和Riemann-Liouville(R-L)定義。本文所采用的是G-L定義,即:

設f（t）在區間[a,t]有m+1階導數,α為任意實數,則α階次的微分定義為:

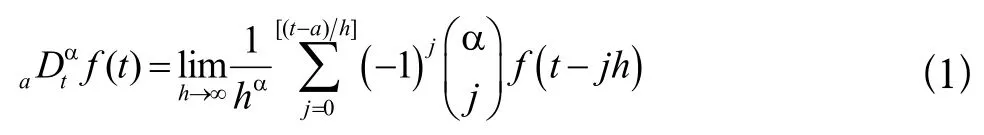
設離散控制系統的狀態方程為:

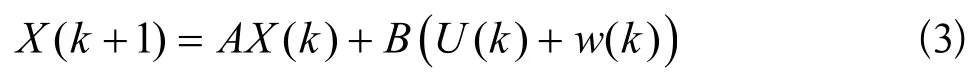
系統的觀測方程為:

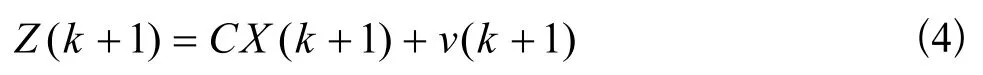
設控制系統的輸出Z(k+1)為實際可測量,卡爾曼濾波遞推算法如下:

設現在系統的狀態是k,可根據系統k時刻狀態預測k+1狀態,即狀態的預測方程為:

狀態更新后,可進一步更新協方差,即協方差的一步預測方程為:

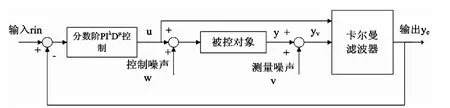
圖1 基于卡爾曼濾波器的分數階PIλDμ控制器的控制原理圖Fig.1 Control schematic of the fractional order PIλDμ controller based on the Kalman filter

濾波增益方程為:

濾波估計方程為:

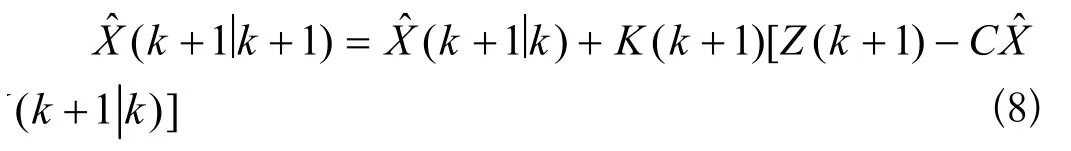
濾波協方差更新方程為:

2 基于卡爾曼濾波器的分數階PIλDμ控制器

基于卡爾曼濾波器的分數階PIλDμ控制原理如圖1所示,其中將連續的被控對象通過零階保持器進行離散,并考慮測量中產生的干擾噪聲v。經過數字分數階PIλDμ控制器的輸出記為u,將其作為被控對象的輸入。

設圖中的連續被控對象為單輸入單輸出系統,其傳遞函數為:

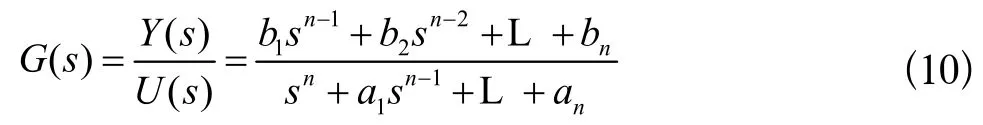
將(10)式轉化為連續系統的狀態方程為:

其中:

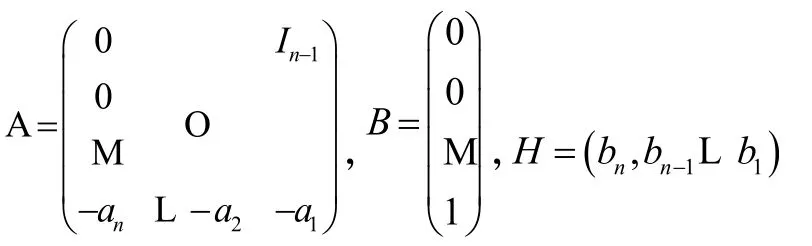
使用零階保持器,建立離散系統狀態空間模型為:

在考慮干擾噪聲時,由(13)和(14)式可得:

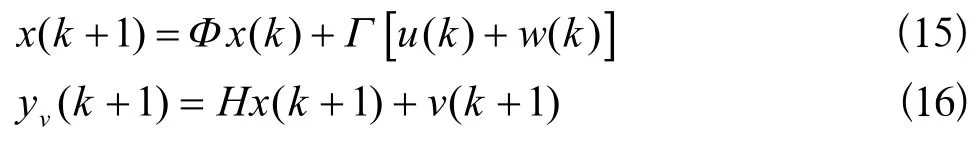
其中:w(k)為控制干擾噪聲,v(k)為測量干擾噪聲。

分數階PIλDμ控制器的時域方程為:

式中:λ和μ分別為分數階PIλDμ控制器的積分階次和微分階次。

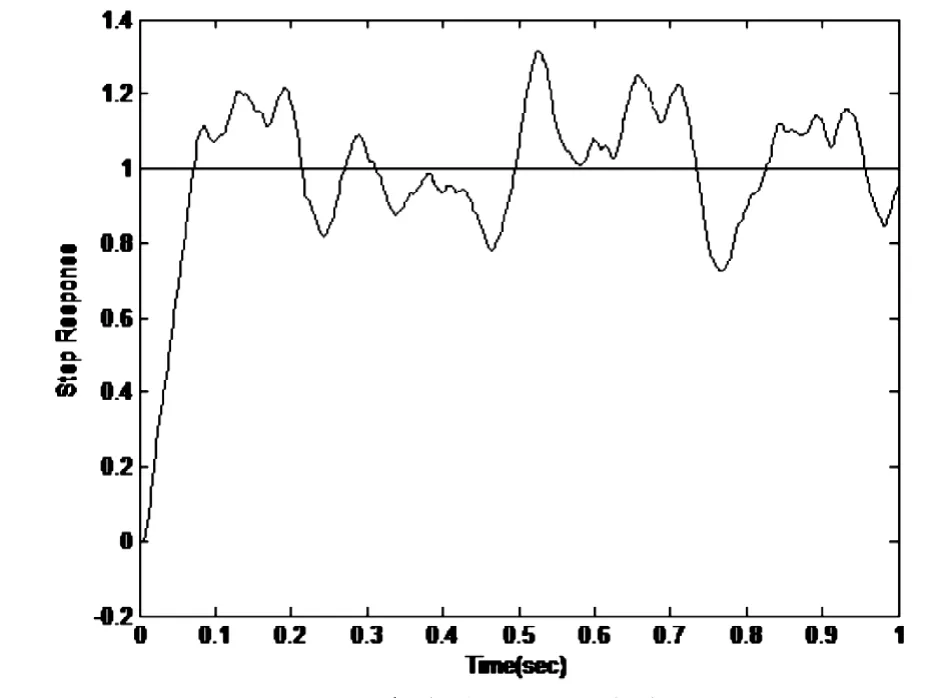
圖2 系統的單位階躍響應圖(未加卡爾曼濾波器的整數階PID控制器作用)Fig.2 The unit step response of the system(integer order PID controller without the Karman filter)

根據α階次的微分定義,結合“短時記憶法”,得到分數階微積分的數字形式為:

其中的二項式系數可通過下式來計算:

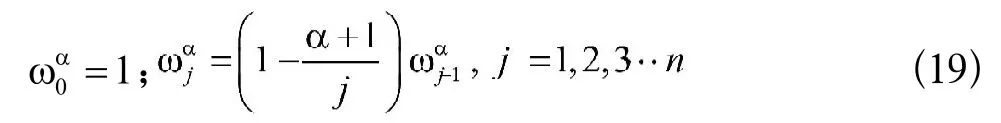
由(17)～(19)式可得,分數階PIλDμ控制器的數字離散形式為:

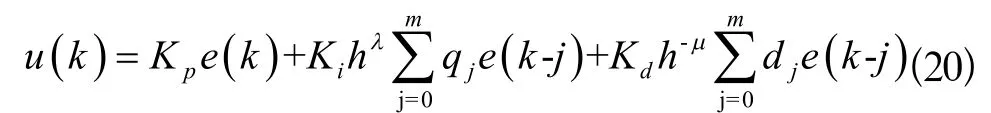
其中:偏差e（k） =rin（k） -ye（k）,qj和dj可通過(19)式計算,ye(k)由下式給出:

綜上,結合公式(5)～(9),對于(15)和(16)式表出的系統,給出卡爾曼濾波算法如下:

表1 系統加入濾波器后在不同控制器作用下的性能指標Tab.1 The performance indicator of the system under different controller with the filter

圖3 系統的單位階躍響應圖(基于卡爾曼濾波器的整數階PID控制器作用)Fig.3 The unit step response of the system(integer order PID controller based on the Kalman filter)

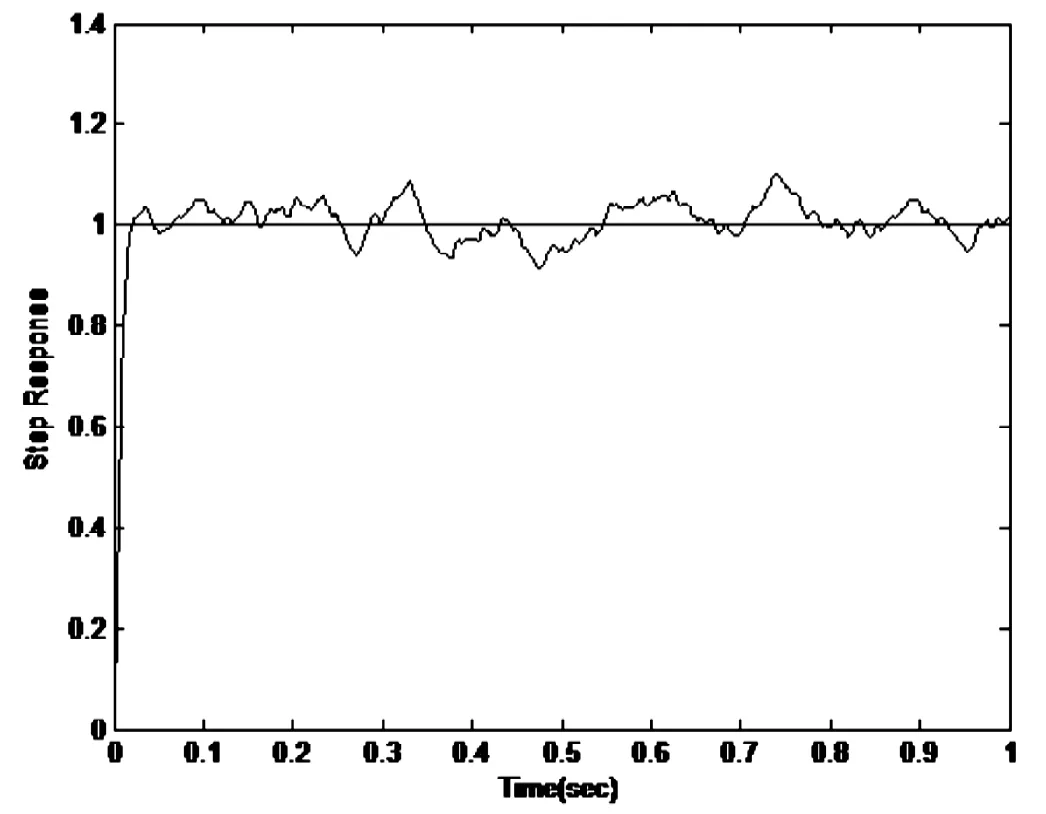
圖4 系統的單位階躍響應圖(未加卡爾曼濾波器的分數階PIλDμ控制器作用)Fig.4 The unit step response of the system(fractional order PIλDμ controller without the Karman filter)

3 仿真算例

例:設被控系統的傳遞函數為[4]:

測量干擾噪聲信號的幅值為0.003,協方差R為1;控制干擾噪聲信號的幅值為0.003,協方差Q為1。

對此被控系統,采用文獻[4]中遺傳算法設計的整數階PID控制器和分數階PIλDμ控制器的傳遞函數分別為:

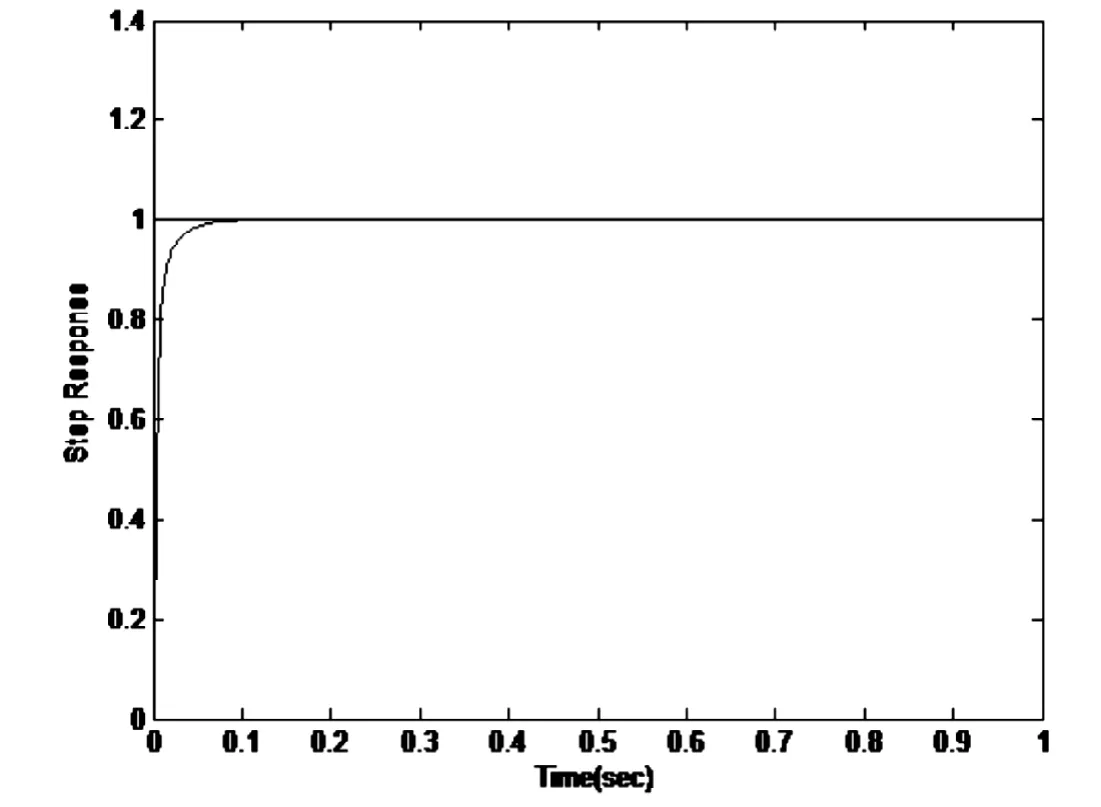
圖5 系統的單位階躍響應圖(基于卡爾曼濾波器的分數階PIλDμ控制器作用)Fig.5 The unit step response of the system(fractional order PIλDμ controller based on the Kalman filter)

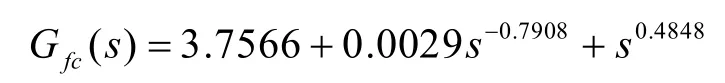
仿真結果見圖2-5,從中對比可知,在考慮過程噪聲和測量噪聲時,若不加卡爾曼濾波器,分數階PIλDμ控制器和整數階PID控制器均不能很好地發揮控制作用。反之,在加入卡爾曼濾波器后,控制器既能很好地控制被控對象,使系統具有良好的控制性能,又可有效地濾除干擾噪聲。仿真結果表明基于卡爾曼濾波器的分數階PIλDμ具有很好的控制性能。

系統加入濾波器后在不同控制器作用下的主要時域性能指標見表1,從中分析可知基于卡爾曼濾波器的分數階PIλDμ比基于卡爾曼濾波器的整數階PID控制器具有更好的控制性能。

4 結論

通過仿真對比表明:對于相同的被控對象,分數階PIλDμ控制器具有良好的控制性能,同時在系統存在干擾噪聲的情況下,加入卡爾曼濾波器可有效地濾除噪聲,使系統具有良好的控制性能。