理解等積變形的轉(zhuǎn)化思想

文|田秋月

平面圖形總復(fù)習(xí)時(shí)，會(huì)遇到無法利用常規(guī)方法計(jì)算面積的復(fù)雜圖形，怎樣利用等積變形將復(fù)雜問題變簡(jiǎn)單？教師可設(shè)計(jì)以下學(xué)習(xí)活動(dòng)。

一、情境中找方法

出示“曹沖稱象”的圖片，請(qǐng)學(xué)生敘述操作要點(diǎn)。

引導(dǎo)學(xué)生發(fā)現(xiàn)，借助水中的船，將無法分割的大象轉(zhuǎn)化成同等質(zhì)量的石頭，啟發(fā)學(xué)生將這一方法應(yīng)用于數(shù)學(xué)問題的解決中。

二、轉(zhuǎn)化中尋策略

1.利用底高關(guān)系進(jìn)行轉(zhuǎn)化。

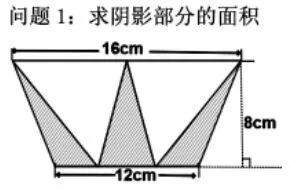
圖1

方法2：轉(zhuǎn)化法。將兩個(gè)小三角形進(jìn)行等積變形，陰影部分轉(zhuǎn)化為底是12cm、高是8cm 的大三角形。學(xué)生發(fā)現(xiàn)借助平行線“軌道”，可以將三角形作等底等高的等積變形，轉(zhuǎn)化成已知底與高的三角形來計(jì)算面積。

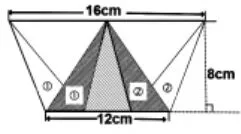
圖2

2.利用等量代換進(jìn)行轉(zhuǎn)化。

出示問題2，組織學(xué)生思考并交流。

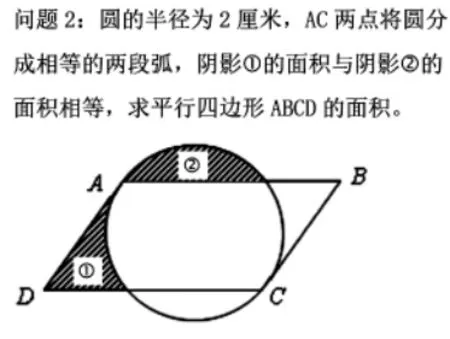
圖3

本題對(duì)于部分學(xué)生來說可能會(huì)有困難，無法直接運(yùn)用面積公式，也無法通過總面積減部分面積來求平行四邊形的面積。

教師可以引導(dǎo)學(xué)生觀察圖中各部分之間的面積關(guān)系（圖4），因?yàn)锳、C 兩點(diǎn)將圓分成兩段相等的弧，可以判斷線段AC 通過圓心，所以S①=S③，S②=S④；又因?yàn)镾①=S②，所以S①=S②=S③=S④。從圖中可知S平行四邊形=S①+S③+S⑤, 等量代換后可得S平行四邊形=S②+S④+S⑤=S圓，這樣就將問題轉(zhuǎn)化為簡(jiǎn)單的圓面積計(jì)算了。

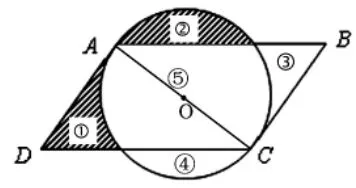
圖4

3.利用等式關(guān)系進(jìn)行轉(zhuǎn)化。

出示問題3（圖5），組織學(xué)生思考并交流。

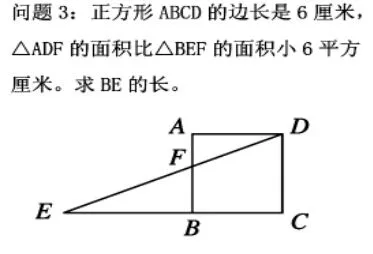
啟發(fā)學(xué)生思考，S△BEF-S△ADF=6cm2，如果這兩個(gè)三角形都補(bǔ)上梯形BCDF，則分別得到了三角形ECD 和正方形ABCD，且這兩個(gè)圖形的面積也相差6cm2，所以S△ECD=S正方形+6=6×6+6=42cm2。求得了△ECD 的面積，可根據(jù)DC 的長(zhǎng)度求出EC 的長(zhǎng)度，從而求得BE 的長(zhǎng)度。

學(xué)生在本題中利用等式構(gòu)建了新的面積關(guān)系，轉(zhuǎn)化得出未知三角形的面積，從而解決相關(guān)問題。

三、聯(lián)系中悟思想

梳理三個(gè)問題的解題思路（圖6），引導(dǎo)學(xué)生感悟不同解題策略和方法間的聯(lián)系與區(qū)別。

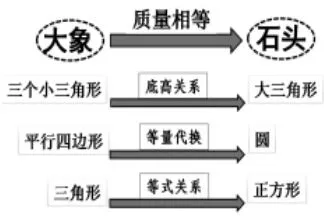
圖6

建立聯(lián)系：學(xué)生發(fā)現(xiàn)，正如“曹沖稱象”，將所求圖形的面積（大象）轉(zhuǎn)化成可計(jì)算的、易操作的常規(guī)圖形（石頭）的面積。

尋找區(qū)別：不同問題所采用的轉(zhuǎn)化策略不盡相同，根據(jù)解題需要靈活選擇等積變形的方法。

在平面圖形的復(fù)習(xí)中，利用等積變形的轉(zhuǎn)化思想，可以更好地發(fā)展學(xué)生的空間觀念和思維能力。