基于激光點熱源非穩態傳熱模型測固體材料熱物性參數

陳清華，高 偉，蘇國用，關維娟，秦汝祥，季家東，馬楊斌

(1. 安徽理工大學 省部共建深部煤礦采動響應與災害防控國家重點實驗室，安徽 淮南 232001；2. 安徽理工大學 礦山智能裝備與技術安徽省重點實驗室，安徽 淮南 232001；3. 達姆施塔特工業大學 材料科學學院，德國 達姆施塔特 D-64287)

隨著材料科學的不斷發展，各種新型材料層出不窮，材料的熱物性是材料的重要特征參量，因此，材料熱物性測試方法的研究受到持續關注[1-6].相對于非穩態熱線法和平面熱源法，激光法避免了熱源與試樣之間的接觸熱阻以及熱源自身熱容所帶來的測試誤差問題，且具有測試周期短、溫度范圍寬、對試樣無熱損傷等一系列優點，在金屬材料[7]、多孔介質[8]、多孔復合材料[9]、巖石[10]、陶瓷[11-12]等固體材料熱物性測試中得到了廣泛應用.經過多年不斷地發展和完善，激光法已形成較為成熟的測試技術體系，并發布了標準[13]，歐美國家大部分熱擴散率等數據均采用此方法獲取.然而，激光閃射法在原理上要求脈沖熱量均勻地作用在被測試樣表面，對材料表面的平整度要求較高，試件制作過程相對復雜.同時，由于激光閃射法對測試時間精度、數據采集瞬時性和精度等均要求極高，儀器價格通常從幾十萬至百萬不等，小型科研機構往往難以承擔如此高昂的設備費用，這一定程度上限制了其推廣應用.

本文提出一種基于激光點熱源非穩態傳熱模型的測試方法，并研制了熱物性參數測試裝置.利用激光發生器發射激光束作用在試樣表面形成點熱源，同時測試試樣表面處的溫升變化，計算試樣導熱系數等熱物性參數.通過對硼硅玻璃(Pyrex7740)標準試樣進行熱物性測試實驗得到的導熱系數測試值與參照值相對偏差最大為2.65%，并進一步對大理石、硅藻土耐火磚、硅磚等進行熱物性測試綜合實驗，測試精度均滿足要求(誤差小于5%)，但裝置硬件成本卻大大降低(硬件成本僅約2萬元).

1 原理模型及數值方法

1.1 物理模型

如圖1所示，以激光點熱源加熱薄平板的一頂角為坐標原點，建立三維坐標系Oxyz，平板上表面為絕熱邊界BB′，下表面為絕熱邊界CC′，長為L，高為H，如果L?H，則可視為無限大平板.入射激光通過逆韌致吸收過程在材料表面趨膚深度內被吸收，并在亞納秒時間內轉化為熱能[14].同時，由于作用在試樣的激光斑點很小，面積可以忽略不計，可視為一點熱源對試樣進行加熱.當熱源持續加熱，熱量傳遞至試樣厚度絕熱邊界后，因無法繼續傳遞而會發生熱量積聚現象，并對試樣內溫度場產生顯著影響.對于熱穿透現象造成的熱量積聚效應，目前通常采用控制測試時間[15]的方法消除由此帶來的誤差.

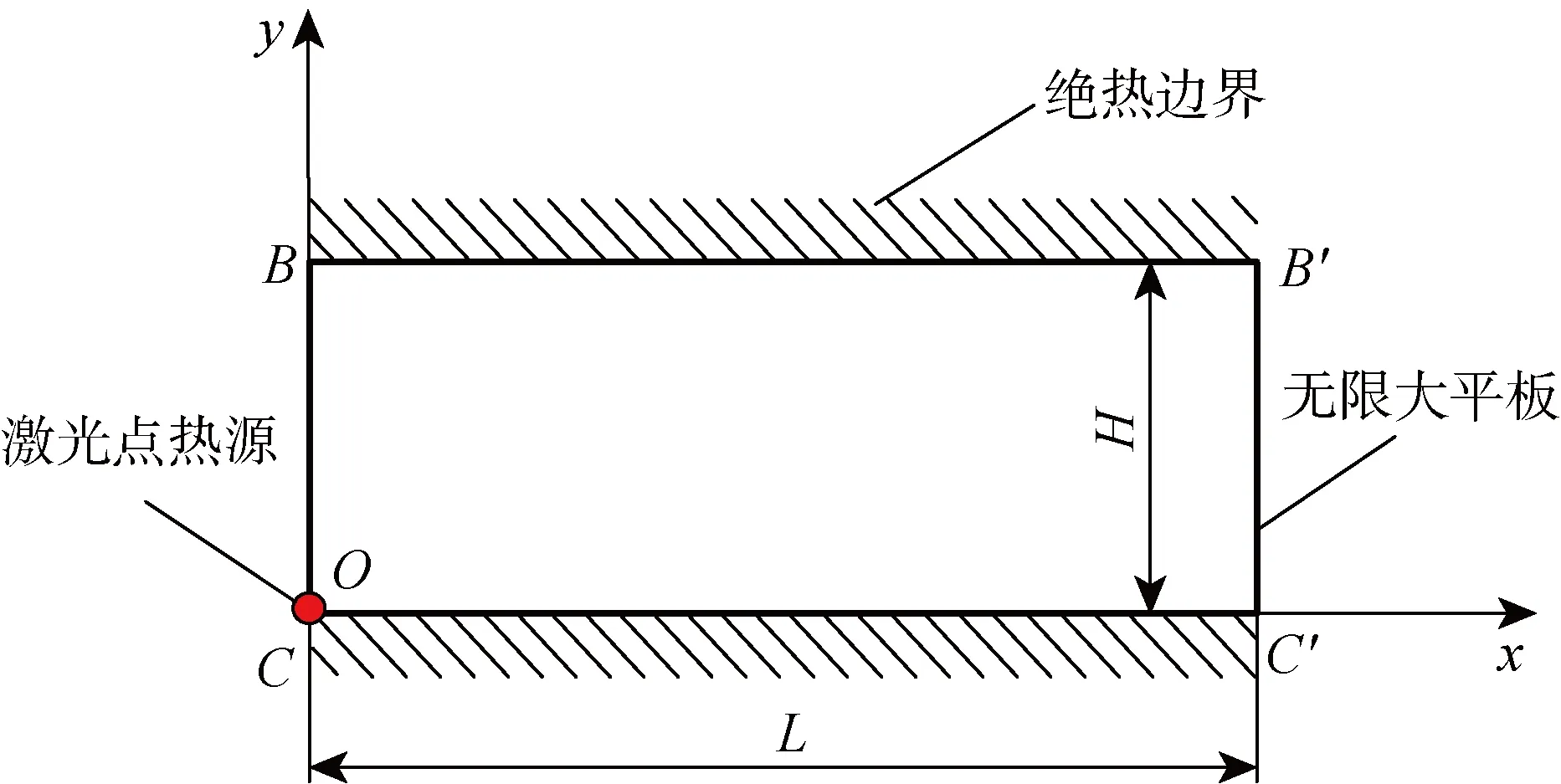
圖1 點熱源作用無限大平板傳熱物理模型Fig.1 Physical model of heat transfer with an infinite large plate by point heat source

1.2 數學描述

設無限大平板的初始溫度為t0，在x=0、y=0、z=0處，有一功率為P的點熱源持續加熱，加熱時間為τ，任意點(x,y,z)處溫升θ的數學模型為

(1)

式中：α為熱擴散率.

令R2=x2+y2+z2，其定界條件為

τ=0，R≥0：θ(R,τ)=0

(2)

(3)

式中：θ(R,τ)為試樣中距熱源距離為R、加熱時間為τ的點的溫升；λ為導熱系數；A為激光作用在試樣上的面積；C為常數.

(4)

式中：θτ為溫升對時間的導數，θτ=dθ/dτ.

采用分離變量法，可得式(4)在定解條件下的解析解：

(5)

式中：erf為誤差函數.

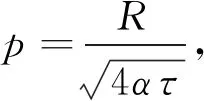
如測得θ(R,τ)和θ(R,2τ)，借助計算機編程，即可由式(7)得到α，再根據式(6)，即可計算出λ.在試樣材料α、密度ρ和λ等已知的情況下，比熱容c即可通過c=λ/(ρα)求出.

1.3 絕熱邊界處熱量積聚效應修正

試樣絕熱邊界處的熱量積聚效應客觀存在，并會造成試樣溫升大于理論值.針對此，文獻[16]將絕熱邊界設想成一面鏡子，在與真實熱源Q相對稱位置處設有一個鏡像熱源Q′，真實熱源與鏡像熱源在絕熱邊界處產生的熱流量沿絕熱面方向相反，當邊界完全絕熱時，鏡像熱源的加熱功率P′等于真實熱源的加熱功率P.如圖2所示，Q與Q′對稱分布，真實熱源與絕熱邊界上一點的距離為RA，引起該點的溫升為θA，因該點溫升是由真實熱源和鏡像熱源共同作用，故該點的真實溫升為2θA.同時可得到試樣上任意一點M的真實溫升θM:

θM(R,τ)=θ(R,τ)+θ′(R′,τ)

(8)

式中：θ(R,τ)為真實熱源引起M點的溫升；θ′(R′,τ)為鏡像熱源引起M點的溫升；R′為鏡像熱源與點M的距離.

圖2 真實熱源及鏡像熱源溫升分布Fig.2 Temperature rise distribution of true heat source and enantiomorphism heat source

若被測試樣長寬遠大于厚度，側向絕熱邊界對應的鏡像熱源對溫升貢獻將非常小，可以忽略，因此可只考慮厚度方向的鏡像熱源影響.

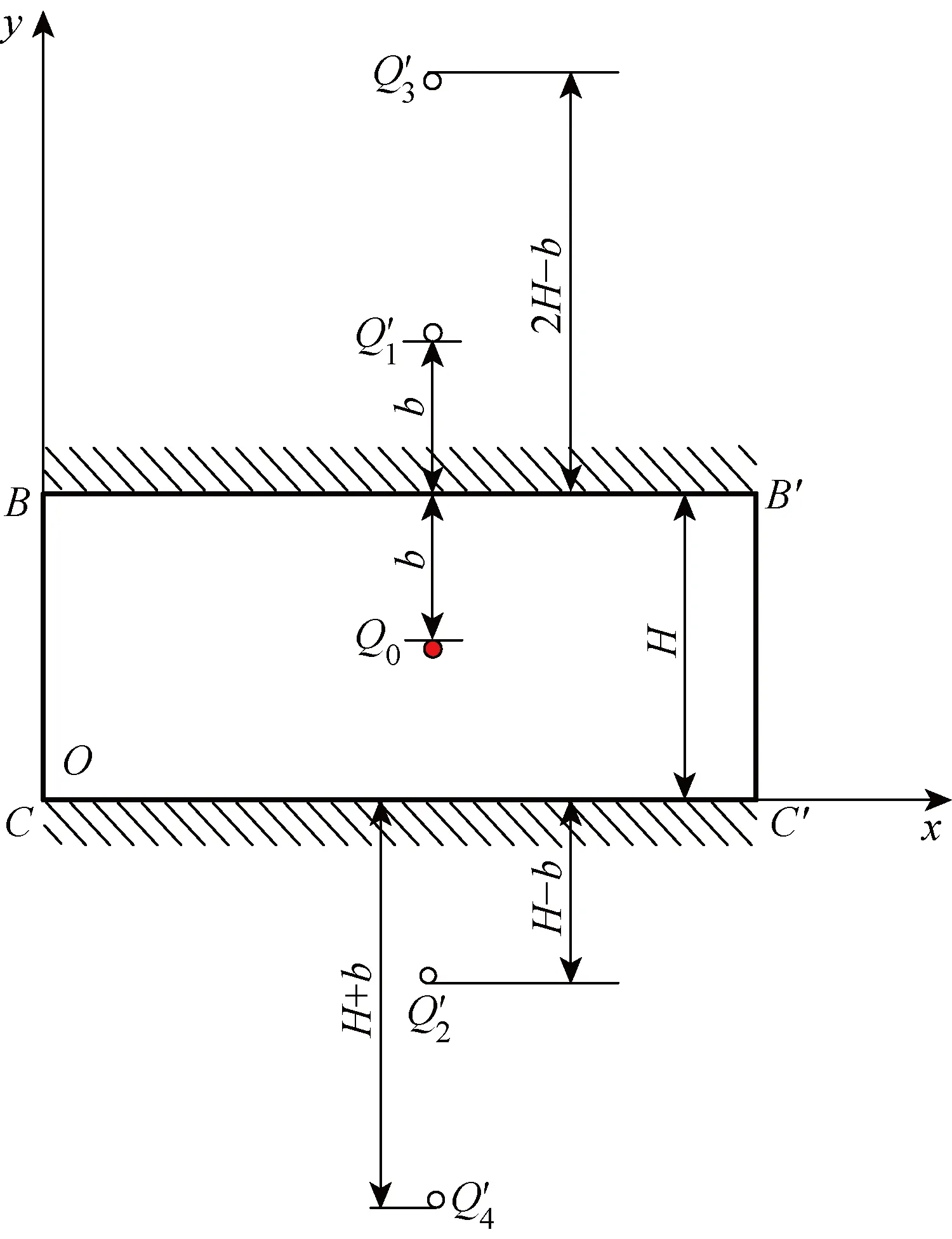
圖3 鏡像熱源分布示意圖Fig.3 Distribution diagram of enantiomorphism heat source

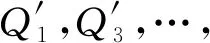
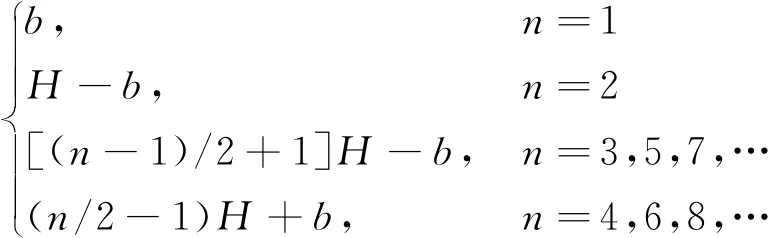
(9)

式中：n為鏡像熱源的序號.

因此，當任意點M位于絕熱邊界上時，該點溫升由真實熱源與鏡像熱源共同作用，且兩者與絕熱邊界的距離相等，即R=R′，則θ(R,τ)=θ′(R′,τ).同時，當熱源位于絕熱邊界時，即真實熱源與鏡像熱源重合在一起，都位于絕熱邊界上，此時，導熱體內任意點將同時受到這兩個熱源的影響且作用強度相等，也滿足θ(R,τ)=θ′(R′,τ).而當激光點熱源作用于試樣的一個頂角時，鏡像熱源分布如圖4所示.

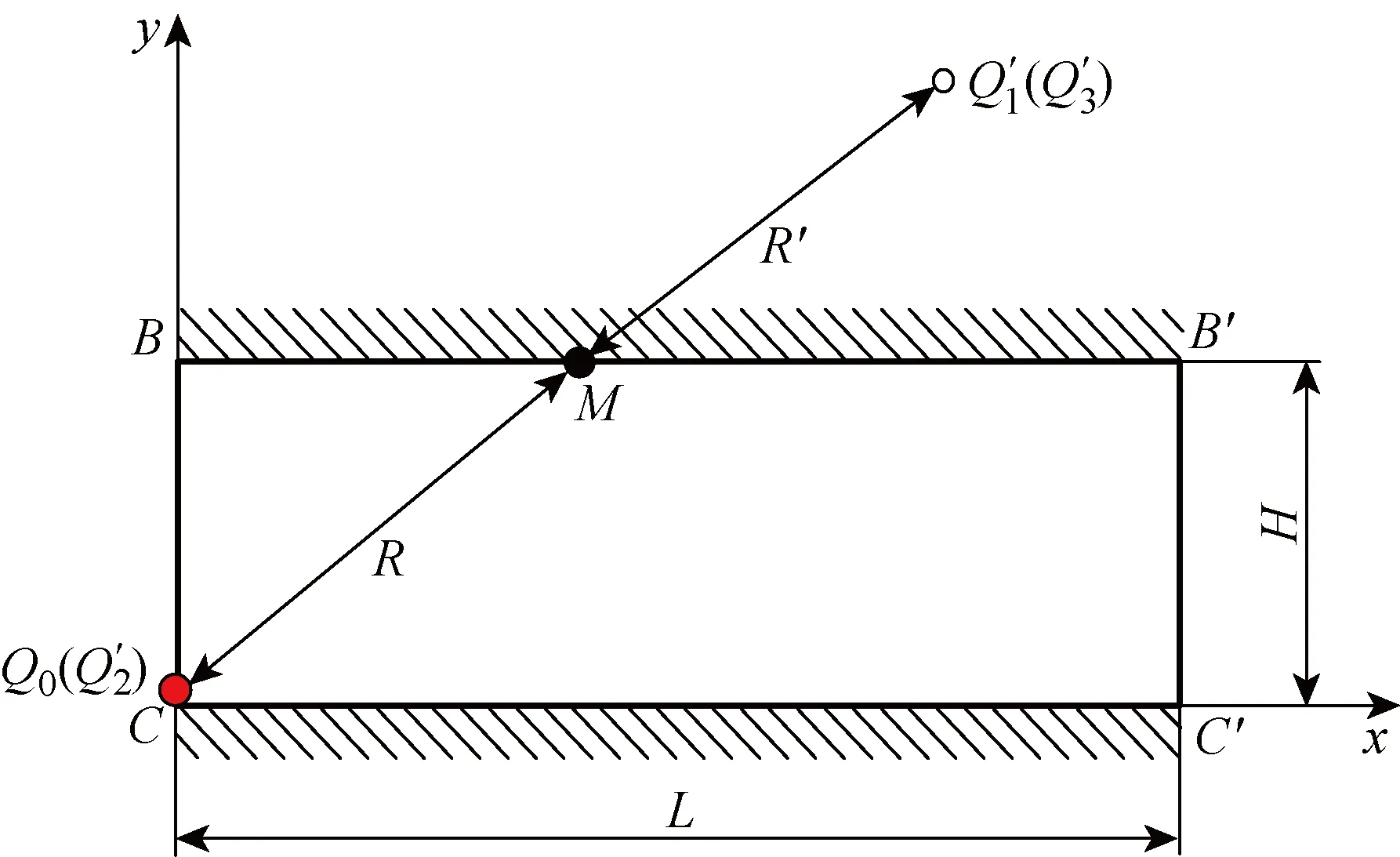
圖4 點熱源位于試樣頂角的鏡像熱源分布圖Fig.4 Enantiomorphism heat source distribution diagram with point heat source at the top corner of the sample

由于真實點熱源位于絕熱邊界上，可得到各鏡像熱源距另一絕熱邊界上任意一點M的距離關系.引入取整函數，得

(10)

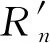
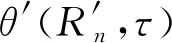
(11)

在連續加熱τ秒后點M的溫升為

(12)

在進行理論溫升計算時，需依據鏡像熱源理論對計算溫升進行修正，以減小測試誤差.試算表明，僅需要利用與測點最近的鏡像熱源(2～3個鏡像熱源)即完成1次修正.然而，隨著測試時間的增長，由于更遠處的鏡像熱源對測點產生的影響會逐漸增強，需要判斷相鄰兩次修正計算結果之間的相對偏差Δd是否滿足測試精度ε的要求，如果偏差較大，則需引入更遠處的鏡像熱源進行二次修正，具體程序如圖5所示.

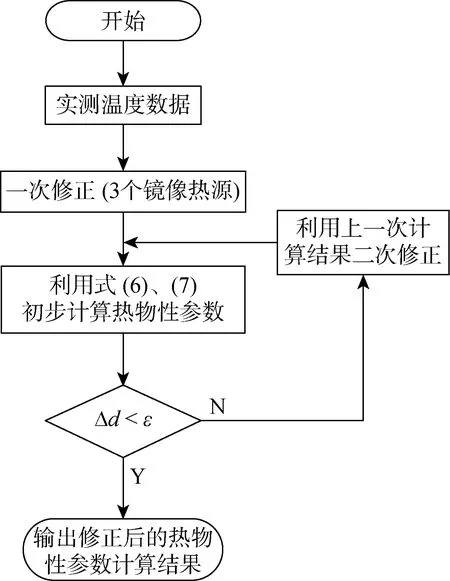
圖5 測試數據修正流程Fig.5 Revise procedure of tested data

2 測試系統設計

測試系統主要由實驗箱、加熱裝置及數據采集系統組成，裝置結構原理如圖6所示.

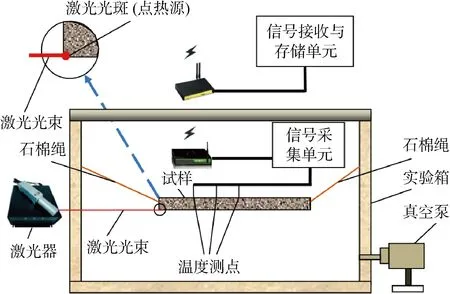
圖6 裝置結構原理圖Fig.6 Schematic diagram of device structure

(1) 實驗箱.實驗箱是由厚度為18 mm的亞克力板制成，為了保證試樣絕熱邊界條件，要求實驗時箱體內部為真空環境.箱體的上端蓋為橡膠材質，端蓋上安裝用于控制箱體內部真空度的壓力控制閥，并通過密封管與370 W的2F-2C-N雙級旋片式真空泵相連.為了盡量降低激光穿過箱體時的能量損失，在激光穿透箱體的入射位置處開有激光通道，且在通道入口鑲嵌鍍膜激光鏡片.

(2) 加熱裝置.采用STL915TI-25.0 W型光纖耦合激光系統提供點熱源，激光器功率0～25 W可調.作用在試樣上的光斑大小可根據激光發射頭與試樣間距離進行調節.將試樣的1個頂角磨出稍大于激光點熱源面積的作用區域，并涂抹石墨粉.激光鏡頭發出激光，穿過鑲嵌在實驗箱體表面的鍍膜激光鏡片后照射在箱體內的被測試試樣的作用區域，實現加熱過程.

(3) 數據采集系統.測溫選擇貼片式PT100鉑電阻溫度傳感器，測溫精度為0.1 ℃，將傳感器布置在距離熱源為R的試樣上表面.采集的數據由A/D數據轉換，經過單片機處理后由信號采集單元，通過Zigbee模塊無線傳輸到計算機中的LabVIEW開發的采集界面進行保存和顯示.

(4) 試樣安放與位置調節.如果把試樣直接放置在支架上，試樣會與支架結構件發生傳熱，進而影響試樣的絕熱條件.在實驗箱體兩側各安裝兩只飛輪，分別系有低導熱系數的無塵石棉細繩，石棉繩托起試樣拐角，進而通過繩索收縮可將試樣提升至合適位置.由于繩索導熱系數很小且與試樣接觸面積有限，故認為不會破壞試樣接觸面的絕熱邊界條件.

3 實驗及結果分析

3.1 不同試樣溫升規律分析

由式(5)可知，溫升θ是關于變量P、R、λ、α及τ的函數，也是材料熱物性參數的最直觀表征，溫升數據直接決定測試結果準確性.P和R是由實驗條件決定.考慮到研究結論普適性，分別選用導熱系數為0.227 W/(m·K)的硅藻土耐火磚[17]、導熱系數為2.7 W/(m·K)的大理石[18]、導熱系數為16 W/(m·K)的304不銹鋼[19]和導熱系數為398 W/(m·K)的純銅[18]進行研究.由于過大的加熱功率會改變材料的自身性質影響溫升，所以激光功率采用5 W，測點距熱源0.02 m，代入式(5)得到圖7所示的溫升曲線.

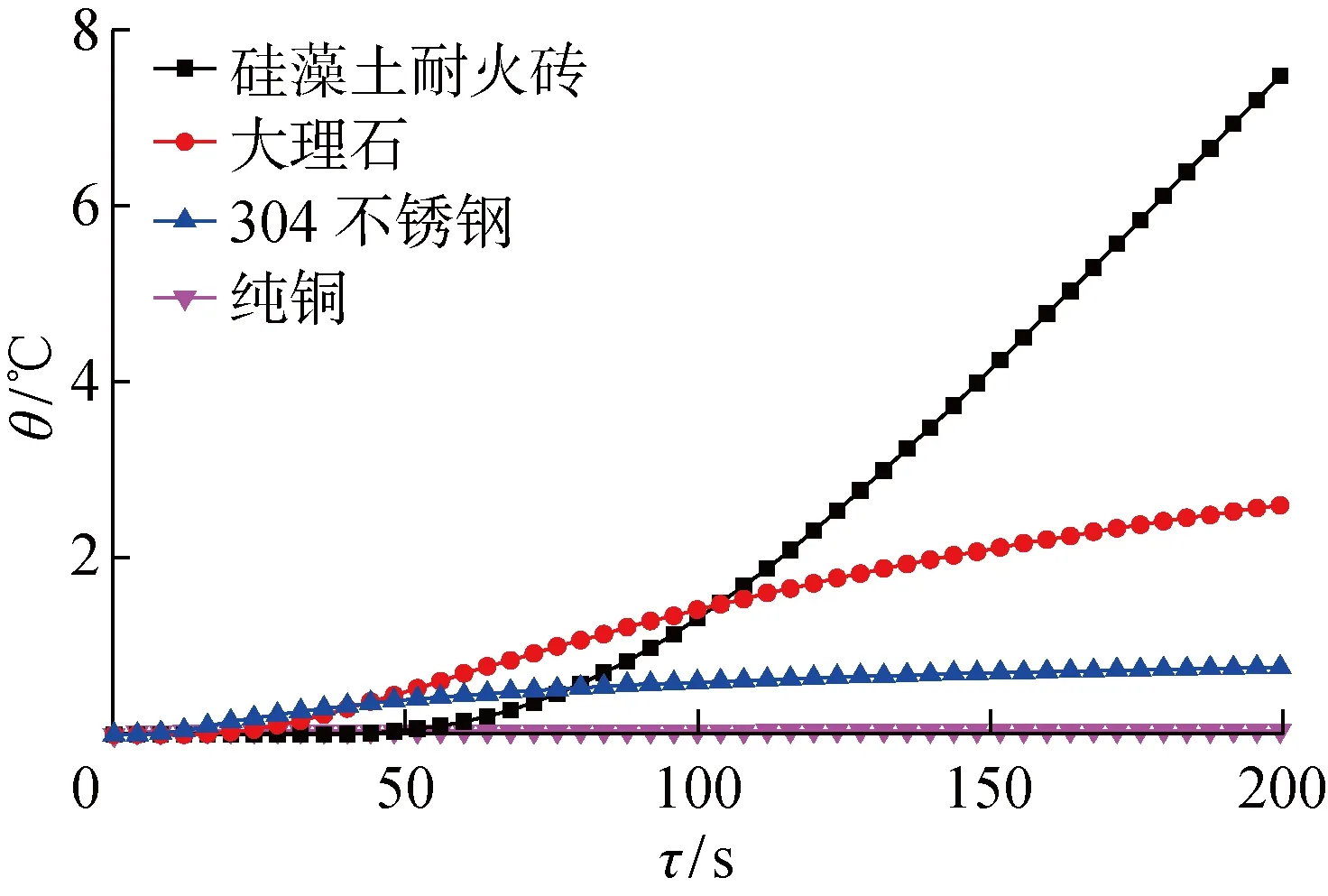
圖7 不同材料溫升曲線圖Fig.7 Temperature rise curves of different materials

由圖7可知，試樣溫升隨導熱系數的增大而急劇減小，硅藻土耐火磚和大理石具有明顯的溫升且上升時間長，因此易獲得多組具有較大溫度梯度的溫升數值，將所得數據帶入式(7)求解熱物性參數時有利于減小測算誤差.而加熱導熱系數較大的材料時，材料測點溫升不明顯，且趨于穩定的時間短.此外，304不銹鋼初始溫升較快，但隨加熱時間增長溫度上升平緩，在持續加熱200 s時溫升僅為1.3 ℃，很難獲得較多的有效溫升數據求解參數.對于導熱系數最大的純銅，因其熱阻極小，在測點處幾乎無溫升，無法求解熱物性參數.綜上，本裝置應用于導熱系數較大的材料時，熱物性測試精度可能會難以保證，對此將通過材料熱物性測試綜合實驗分析和系統熱物性測試結果不確定度分析進一步驗證.

3.2 標準試樣熱物性測試實驗

選擇長、寬為100 mm，厚度為4 mm的硼硅玻璃(Pyrex7740)作為試樣，密度為 2 250 kg/m3，環境溫度為27 ℃.實驗前，將箱體內抽成低真空環境.在試樣上表面均勻布置3個溫度測點，編號為1#、2#和3#，并取平均值作為最終實測溫度.

對同一種試樣在相同條件下進行3次實驗，用導熱系數的相對偏差Δλd來衡量單次測定結果對平均值的偏離程度，實驗結果的可重復精度可表示為

(13)

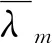
表1為硼硅玻璃(Pyrex7740)熱物性參數計算結果.可以看出，該測試可得到導熱系數的最大相對偏差3.48%，滿足熱物性測試國家標準.取多組熱物性參數值的平均值作為最終的測算結果，則硼硅玻璃(Pyrex7740)的熱擴散率為6.15×10-7m2/s，熱導率為1.100 W/(m·K)，與文獻[18]硼硅玻璃(Pyrex7740)的熱導率1.13 W/(m·K)較為吻合，兩者之間的相對偏差為2.65%.

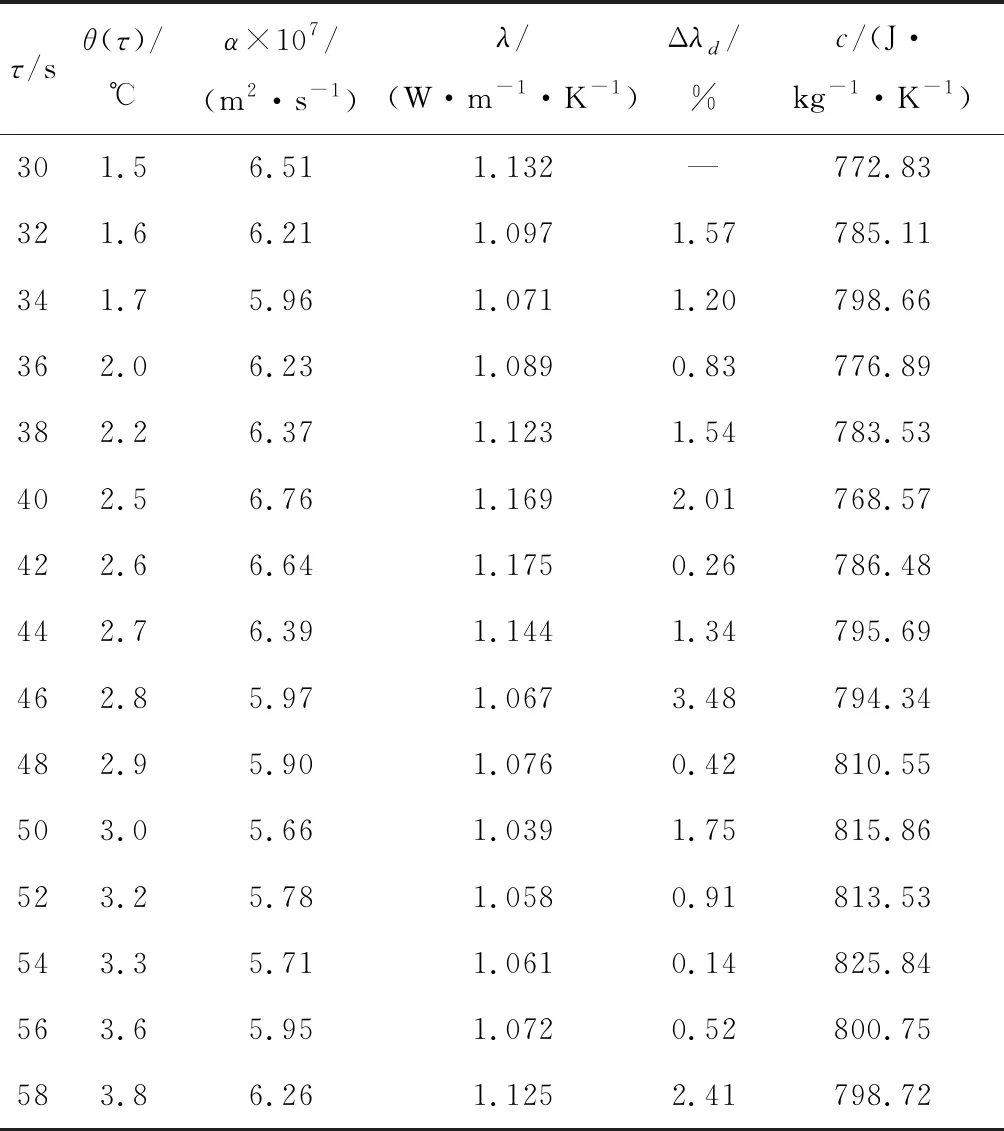
表1 硼硅玻璃(Pyrex7740)熱物性參數計算結果

3.3 材料熱物性測試綜合實驗分析

為進一步驗證本測試方法，分別選用導熱系數較小的大理石、硅藻土耐火磚和硅磚，以及導熱系數較大的鋯質磚進行實驗.大理石長為112 mm，寬為112 mm，厚度14 mm，密度為 2 632 kg/m3；硅藻土耐火磚長為112 mm，寬為112 mm，厚為14 mm，密度為696 kg/m3；硅磚長、寬均為100 mm，厚10 mm，密度為 1 700 kg/m3；鋯質磚長為100 mm，寬為 1 000 mm，厚10 mm，密度為 2 680 kg/m3.對各材料的同一試樣均在相同條件下進行3次測算，以檢驗計算結果可重復性，結果如表2所示.測試結果與相關文獻對比結果結果如表3所示.

由表2可以看出，低導熱系數材料的參數測試結果與平均值最大相對偏差分別為0.18%、3.24%及1.78%，可重復精度符合標準要求.而導熱系數較大的鋯質磚最大偏差超過了5%，測試結果準確性較差.由表3可知，大理石、硅磚及硅藻土耐火磚導熱系數測試結果與文獻[17-18]數據基本一致，最大相對偏差為2.76%，但導熱系數較大的鋯質磚材料測量結果與文獻[19]中數值相對偏差卻高達6.38%，已超出可接受范圍.利用現有Shotherm QTM-D2型導熱系數速測儀測試大理石試樣導熱系數，并用差熱分析儀測量其比熱容，結果分別為2.763 W/(m·K)和874.8 J/(kg·K)，換算出熱擴散率為1.20×10-6m2/s，與本文方法所測結果較為吻合.

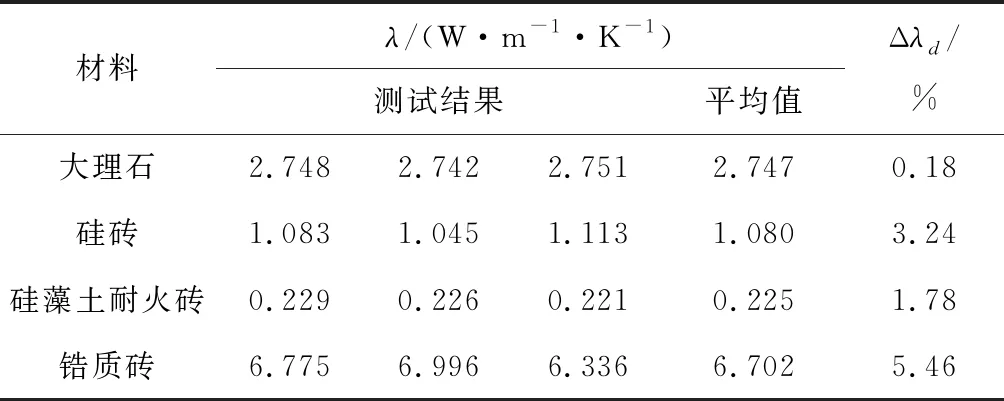
表2 熱物性測試結果可重復性

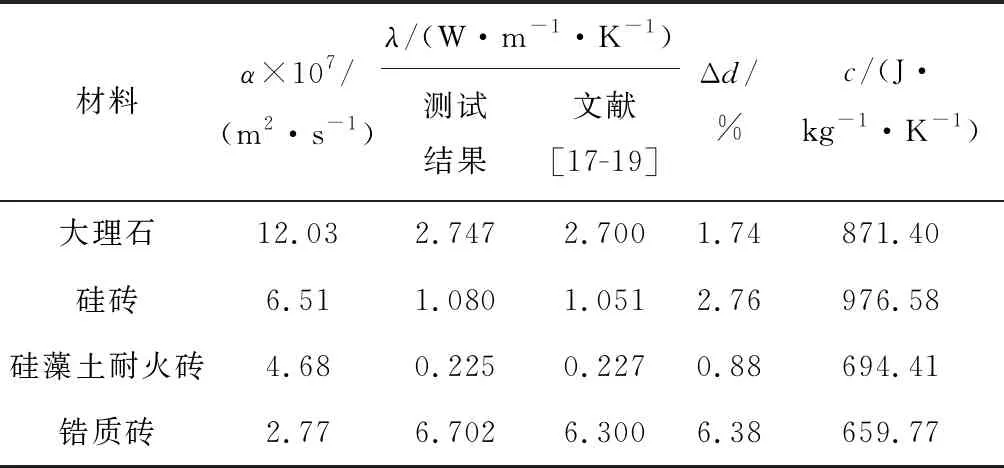
表3 4種材料熱物性測試結果與參考文獻對比

4 系統熱物性測試結果不確定度分析

不確定度可直接表明測試結果的可信賴程度，并可對測量結果的準確程度做出科學評價.本節選擇大理石和普通玻璃為研究對象，進行熱物性測試不確定度分析.

4.1 標準不確定度A類評定

對大理石和玻璃分別在相同實驗條件下，對同一試樣重復測試6次，得到熱擴散率的A類標準不確定度u(α)，結果如表4所示.

表4 大理石和玻璃熱物性參數重復性實驗

4.2 標準不確定度B類評定

由測試原理可知，測試時間、測點與加熱點距離以及試樣厚度的測量、熱源功率、測點溫度和熱擴散率都會影響材料導熱系數的測定，因此需對這些因素進行不確定度分析.

(1) 時間引入的不確定度.測試過程中，時間的不準確會導致數據記錄產生偏差.保證時間的精度不高于2%，包含因子k=2，因此τ的標準不確定度為

(14)

(2) 溫度引入的不確定度.選擇高精度PT100鉑電阻溫度傳感器，并結合溫度變送器等信號采集與傳輸單元與LabVIEW軟件進行通訊，實現對溫度信號的采集與傳輸.測試系統抗干擾性較為優越，選用的二等標準鉑電阻檢定不確定度為0.06 ℃，包含因子k=3，置信概率為99%，則標準不確定度為

(15)

系統選用的溫度變送器精度等級為0.2級，工作范圍在0～200 ℃，根據出廠檢測給定的不確定度為0.03 ℃，包含因子k=2，則標準不確定度為

(16)

則由溫度測定引入的不確定度u(t)為

(17)

(3) 測試距離引入的不確定度.測量實驗厚度以及傳感器測點位置確定所用的游標卡尺的不確定度為0.02 mm，測量范圍為0～300 mm，根據文獻[20]得出游標卡尺的不確定度為0.04 mm，誤差Δ的統計分析如表5所示.取包含因子k=2，則標準不確定度為

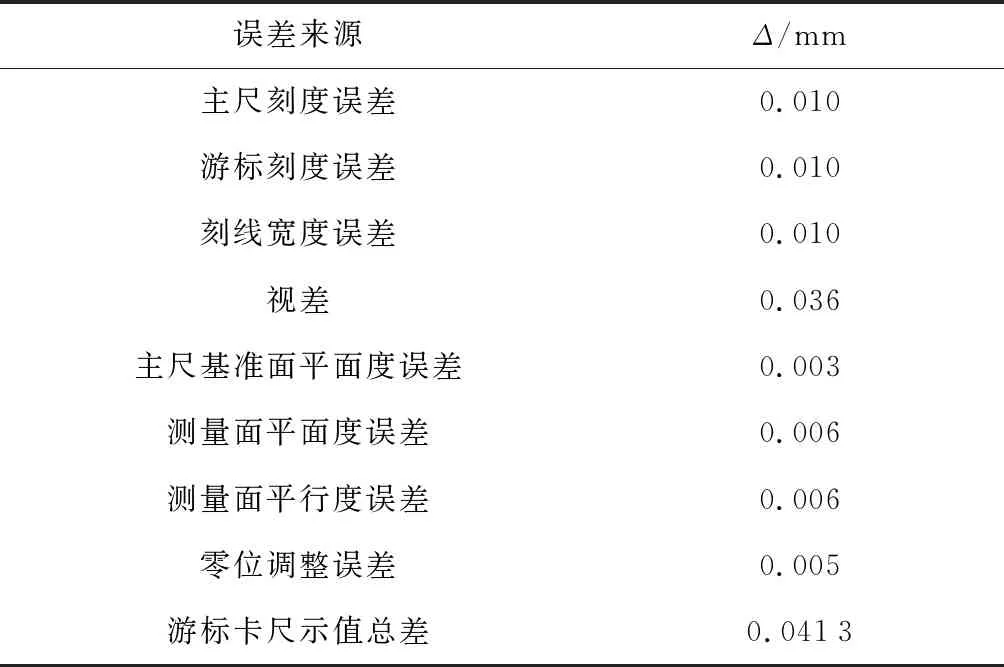
表5 游標卡尺示值總誤差Tab.5 Overall error of vernier caliper indicating value

(18)

(4) 加熱熱源引入的不確定度.本系統選用的光纖耦合激光器根據出廠說明，其功率控制精度為0.05 W，包含因子k=2，標準不確定度為

(19)

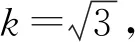
(20)

則合成的加熱熱源不確定為

(21)

4.3 合成不確定度的評定

當被測量中包含多個輸入量時，被測量Y的不確定度由各輸入量X1，X2，…，Xn的不確定度合成[21].為便于對導熱系數λ的測量結果進行評定，引入相對標準不確定度ui(λ)對本系統測試結果進行分析，i表示不確定度來源的序號.根據定義，相對標準不確定度為標準不確定度除以測得值的絕對值.將輸入量的相對標準不確定度適當合成得到合成相對標準不確定度uc(λ)，取影響因子k=2，得到擴展不確定度U，具體計算結果如表6和7所示.

表6 大理石的不確定度分析Tab.6 Uncertainty analysis of marble

表7 玻璃的不確定度分析一覽表Tab.7 Calendar of uncertainty of glass

由表6和7可知，大理石導熱系數的擴展不確定度較大，為16.96%，而玻璃的導熱系數測定結果的擴展不確定度為4.32%.進一步說明本測試系統更適用于低導熱系數(小于3 W/(m·K))的固體材料的熱物性參數測定.

5 結論

利用激光點熱源非穩態傳熱模型和鏡像熱源理論，研制了一套以激光束為熱源、試樣置于真空箱內的測試系統，對固體材料熱物性參數進行測定分析研究，實驗結果驗證了本測試方法的可行性和正確性，主要結論有：

(1) 通過硼硅玻璃等5種材料的熱物性測試實驗發現,導熱系數較小的大理石等材料測試值與參考值的相對偏差不大于2.76%，導熱系數較大的鋯質磚材料的相對偏差達到了6.38%，大于可接受的5%，表明本測試方法對低導熱系數材料具有更高的測試精度.

(2) 對大理石和硼硅玻璃的測試導熱系數值進行不確定度分析發現，導熱系數為2.7 W/(m·K)的大理石的擴展不確定度達到16.96%，而導熱系數相對較小的硼硅玻璃的擴展不確定度僅為4.32%，表明本裝置在測試低導熱系數材料時具有較高的可靠度.結合測試精度，本裝置適用于導熱系數小于3.0 W/(m·K)的固體材料.

(3) 理論上，本文方法應具有較高的測試精度.但傳感器精度、貼敷于試樣表面存在的接觸熱阻以及模型求解算法精度等因素使得本文方法在測試精度方面與其他方法相比并沒有明顯提升.未來工作將從改進溫度信號采集手段、尋求更優的參數求解算法等方面進行完善.