場論視角下的剛體運動學

張新華

(西安交通大學航天學院，西安710049)

剛體運動學是理論力學的重要組成部分。無論是剛體運動的速度分析還是加速度分析，均屬于重點學習內容。本文試圖從場論的觀點出發，審視三維空間剛體運動學中的速度場與加速度場，以期在理論體系上對二者的特性進行更完整的表述。

1 剛體運動速度場與加速度場的分解

如圖 1 所示，剛體運動過程中，按照基點法其上任一點P的速度可以表示[1-2]為

式中，vB為基點B的速度，ω= [ω1,ω2,ω3]T為剛體的角速度矢量。

P點的加速度可表示為

式中，aB為基點B的加速度，ε=[ε1,ε2,ε3]T為剛體的角加速度矢量。

剛體上所有點的速度與加速度分別構成一個光滑連續的矢量場。根據矢量場的 Helmholtz 分解定理[3]，三維空間中的任何光滑矢量場可以分解為一個無旋場(旋度為0 (零矢量))、一個無源場(散度為0)以及一個平庸場(常矢量場，其旋度與散度同時為零) 三者之和。

圖1 剛體運動的速度與加速度分析

對速度場的表達式 (1) 進行分析可知：等式右端第一項vB表示的是基點B的速度。基點選定后，在任意瞬時，其速度對剛體上的其他點而言就是一個不隨空間變化的常矢量(亦即平庸場)，其旋度為0，其散度亦為0。等式(1)右端的第二項表示的是一個有旋場，其旋度為2ω。具體推導與論證見第二節。

另一方面，由場論可知，有旋場存在相應的矢量勢，有源場存在相應的標量勢。據此，剛體運動速度場還可以表示為

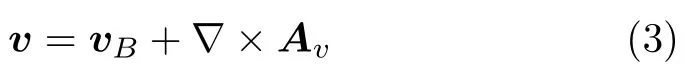
式中，Av為速度場的矢量勢。剛體運動速度場沒有有源場分量，相應的標量勢為0。由觀察可得，矢量勢的表達式為

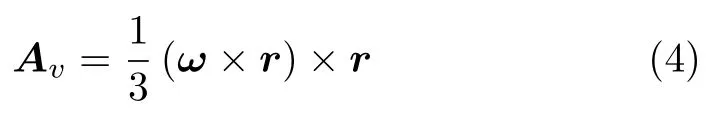
類似地，對加速度場的表達式 (2) 進行分析可知：等式右端aB表示的是基點B的加速度。基點選定后，在任意瞬時，其加速度對剛體上的其他點而言就是一個不隨空間變化的常矢量，其旋度為0，其散度亦為0。等式(2)右端的第二項表示的是一個有旋場，其旋度為 2ε。等式 (2) 右端的第三項表示的是一個有源場，其散度為 ?2|ω|2。具體推導與論證見第二節。

類似于對速度場的分析，剛體運動的加速度場還可以表示為

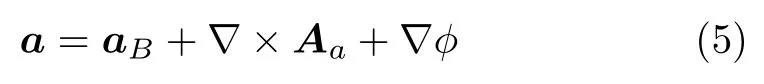
式中，Aa為加速度場的矢量勢；?為加速度場的標量勢。通過觀察可知，Aa的表達式為

?的表達式為

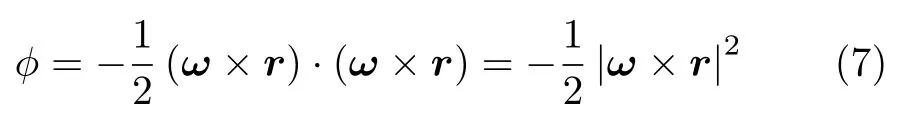
2 速度場與加速度場的旋度、散度與梯度

剛體運動過程中，其上各個質點的速度構成一個矢量場，各個質點的加速度也構成一個矢量場。下面分別推導這兩個矢量場的旋度、散度與梯度的表達式，并對其力學含義予以闡述。

2.1 速度場與加速度場的旋度

速度場的旋度[4]為

由于vB不隨空間變化，其旋度為0。

由式 (8) 可以看出，剛體運動速度場的旋度等于二倍的角速度 (矢量)，這是場論中的一個熟知的結論。

加度場的旋度為

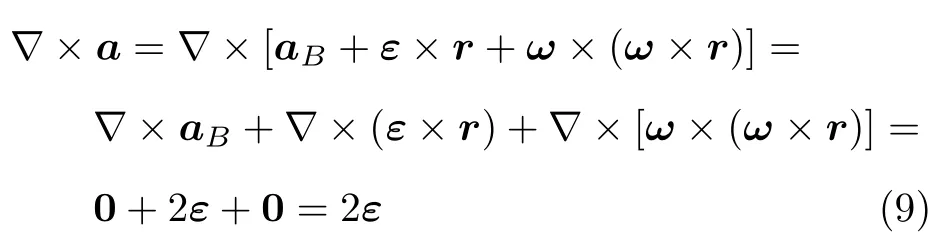
類似于速度場，剛體運動的加速度場的旋度等于二倍的角加速度(矢量)。

2.2 速度場與加速度場的散度

速度場的散度為

式中，vB不隨空間變化，所以其散度為 0。ω也不隨空間變化，其旋度亦為0。按定義計算可知，r(球對稱中心場) 的旋度也為0。

由式(10) 可以看出，剛體運動的速度場是一個無源場。事實上，這也正是剛體的特性之一。如果一個物體運動的速度場是有源場的話，其必然是一個可變形體。

加度場的散度為

由式(11) 可以看出，剛體運動的加速度場是一個有源場。正是這個源項導致旋轉剛體出現了離心力。

2.3 速度場與加速度場的梯度

速度場的梯度可以看作是由梯度算子與速度場構成的一個并矢，亦即一個二階張量，具體表達式為

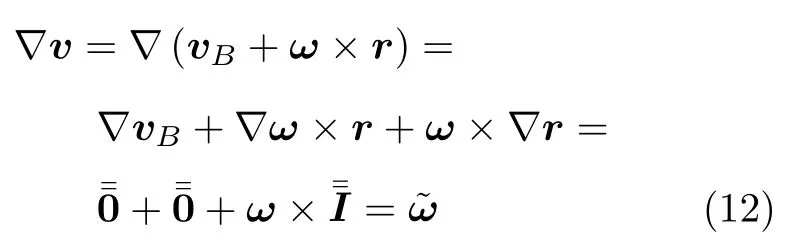
速度場的梯度是一個二階張量，而任一二階張量皆可分解為其對稱部分(張量) 與反對稱部分(張量) 之和。其中，對稱部分表示物質的應變率張量，而反對稱部分則表示物質的旋率張量[6]。式(12) 表明，剛體運動速度場的梯度的對稱部分恒等于零，反映了剛體不會發生變形這一本質特性；而其反對稱部分恰好等于剛體的角速度張量，反映了剛體的旋轉運動特性。

加度場的梯度為

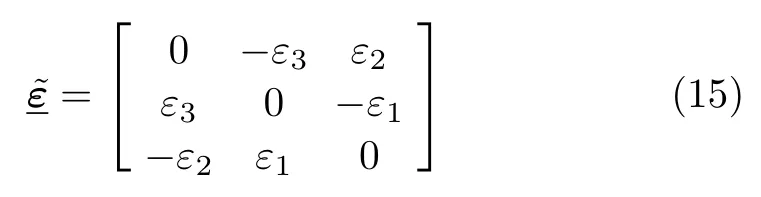
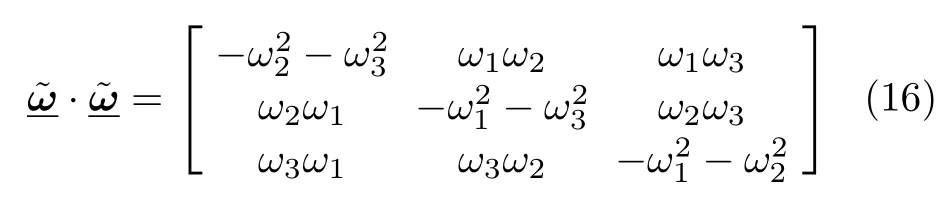
由式(14) 可以看出，剛體加速度場的梯度可以分解為一個對稱張量·和一個反對稱張量之和。其中對稱部分反映了三維空間剛體運動過程中相對法向加速度的空間變化率；而反對稱部分則反映了三維空間剛體運動過程中相對切向加速度的空間變化率，即角加速度張量。當剛體作平面運動時，式 (15) 就自然地退化為僅與標量ε有關的反對稱矩陣，而式 (16) 則退化為僅與標量ω2有關的對稱矩陣。

3 結語

本文基于矢量場的 Helmholtz 分解定理，重新審視了三維空間剛體運動的速度場與加速度場的特性，得到了速度場的矢量勢以及加速度場的矢量勢與標量勢。通過考察剛體運動速度場與加速度場的旋度、散度與梯度，揭示了速度場的旋度與角速度矢量的關聯性以及速度場的梯度與角速度張量的關聯性。速度場的旋度與梯度分別從不同方面描述了剛體的旋轉運動特性。剛體運動速度場的散度恒為零，這反映了剛體運動過程中不會發生變形的特性。剛體運動加速度場的旋度與剛體的角加速度矢量相關聯，而加速度場的梯度則既與角速度張量相關聯，亦與法向加速度空間變化率張量相關聯。剛體運動加速度場的散度與剛體的角速度相關聯，這反映了剛體運動過程中離心力的來源。