冷彎薄壁型鋼受彎構件承載力與延性優化研究

鄧 露，鐘玉婷，楊遠亮，劉艷芝

(1. 湖南大學土木工程學院，長沙 410082；2. 湖南大學建筑安全與節能教育部重點實驗室，長沙 410082)

近年，冷彎型鋼構件已被廣泛應用于建筑、機械和航空工程等多個領域。與熱軋鋼構件相比，冷彎型鋼構件具有輕質高強、運輸安裝方便、節能環保、經濟高效等優點。此外，冷彎型鋼截面形狀在生產加工過程中，具有靈活性和多用性。這些截面形狀是在室溫下通過冷軋或壓彎相對較薄的金屬片獲得的，生產工藝簡單，具有極大的開發及優化的潛力。Krishnan 和Shetty[1]于1959 年首次提出純彎曲情況下進行開口工字型截面薄壁梁優化設計能明顯節約材料成本。因此通過優化冷彎型鋼截面形狀，能夠最大限度地提高材料利用效率以滿足特定目標。

由冷彎型鋼構造的最常見的結構體系是剪力墻體系，主要用于住宅建筑，使用截面尺寸小的超薄構件和半剛性連接是導致剪力墻體系局部過早失效和延性差的主要原因[2]。所以對于冷彎型鋼，有必要像熱軋鋼一樣開發框架體系，不僅空間布置更靈活，與傳統剪力墻體系相比也具有更好的承載力、抗震性能[3]。傳統的由單個構件形成的框架體系，其連接處具有較好的延性，而梁柱保持彈性，不能產生足夠的延性以獲得高抗震性，所以在高震區僅限于單層住宅[4]。近年來，隨著冷彎型鋼框架體系從低層到多層的不斷發展，這類結構對冷彎鋼構件的承載力要求越來越高，與此同時，對構件延性的需求也在不斷增大。

Wong 和Chung[5]提出了背靠背形式的雙肢拼合C 型鋼并開展了一系列相關試驗，結果發現該截面構件表現出不可忽略的延性和耗能，但其寬厚比并不滿足高抗震區設計要求。Sabbagh 等[6]發現雙對稱彎曲翼緣截面比雙拼C 型鋼截面具有更好的強度、剛度和延性，然而考慮到制造和施工限制，這類截面不能廣泛應用。Ye 等[7]開發了一種折疊翼緣截面，承載力比雙拼C 型鋼高出57%，且有平翼緣，方便與樓板連接，比彎曲翼緣更實用。陳明等[8]將冷彎C 型鋼拼合成I 形、L 形、T 形或十字形等組合截面，提高了構件承載力，整體框架抗震性能更佳。隨著計算機技術的發展，學者們通過引入遺傳算法、粒子群算法等開展了更多截面優化的研究[9-10]。

本文選用具有較好屈曲后性能的腹板翼緣加勁截面和腹板加勁的折疊翼緣截面，優化截面尺寸以提高其在單調荷載作用下的承載力及延性。在一定的優化約束條件下，采用已被驗證的有限元模型對這兩種截面進行幾何、材料非線性分析，且考慮了初始缺陷的影響，再結合神經網絡、遺傳算法對截面尺寸進行優化，最后采用TOPSIS 決策出最優截面尺寸。

1 有限元分析

于欣永等[11]發現在卷邊槽鋼的受壓翼緣中間設置加勁肋可以提高構件穩定性。Ye 等[7]開發出的折疊翼緣截面，承載力比雙拼C 型鋼高出57%。但截面翼緣彎折使腹板和翼緣夾角增大，翼緣對腹板支撐減弱，可能導致腹板過早屈曲。因此本文在折疊翼緣截面的基礎上設置腹板加勁肋，對圖1所示的腹板翼緣加勁的槽鋼截面及腹板加勁的折疊翼緣截面開展進一步的優化分析。

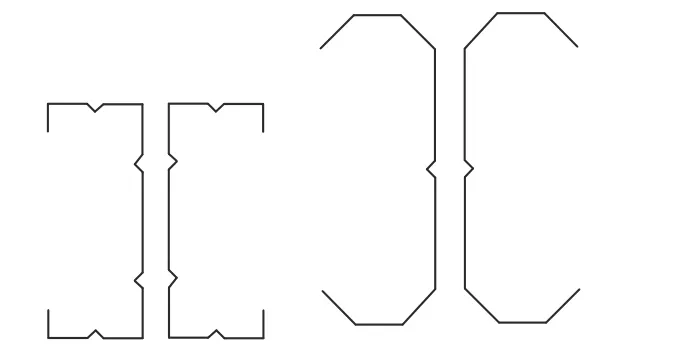
圖 1 截面形狀Fig.1 Cross-sectional shapes

1.1 有限元模型

Haidarali 等[12-14]發現，當采用合適的單元類型、材料參數及缺陷引入方法，利用ABAQUS有限元分析模型就可以精準預測冷彎構件的承載力及屈曲后行為。本文使用已經過試驗驗證的有限元模型[15]，將3 m 長的橫向抗彎框架簡化為1.5 m長的懸臂梁，邊界條件、加載點和約束情況如圖2所示。為了防止側向扭轉，對懸臂梁兩端及中間截面的翼緣和卷邊進行橫向約束，用綁定約束連接兩端及中間截面的腹板，端部施加150 mm 的豎向位移(相當于0.1 rad 轉角)。構件采用S8R5單元模擬，單元尺寸為20 mm×20 mm。構件選用Q345B 鋼種，其本構模型采用雙線性應力-應變模型，彈性模量E 取200 GPa，第二模量Es=E/100，泊松比ν=0.3，屈服強度Fy= 427 MPa，極限強度Fu= 593 MPa。有限元模型中考慮了幾何缺陷的影響，在一階屈曲模態基礎上引入初始缺陷大小，當壁厚t<3 mm 時，依據Schafer 和Pek?z[16]的研究，局部及畸變幾何缺陷大小分別為0.34t和0.94t。

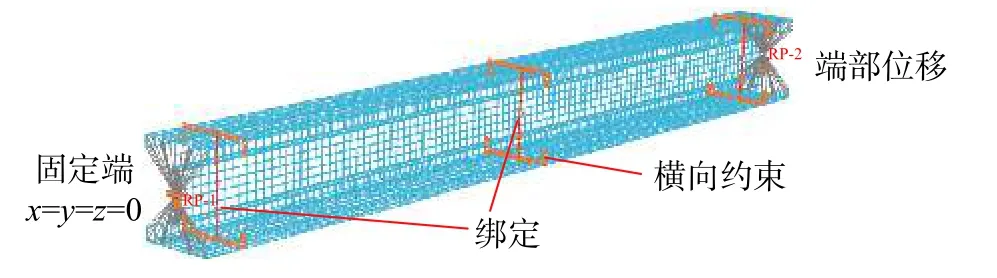
圖 2 有限元模型Fig.2 Finite element model

1.2 截面延性

歐洲規范依據受彎構件的承載力及變形能力將截面分為4 類[17]，Ⅰ類、Ⅱ類截面可以達到塑性彎矩，Ⅲ類、Ⅳ類截面則無法達到。盡管冷彎薄壁型鋼截面不能達到塑性彎矩，無法形成塑性鉸，屬于后兩類截面，但陳以一等[18]研究表明非塑性鉸截面構件的塑性性能也是可以考慮利用的。本文將構件承載力和延性作為優化目標，依據FEMA-356[19]等效雙線性模型(EEEP)計算延性，延性計算公式為：

式中：μ為延性系數；θt為目標轉角，其取值為是真實彎矩-轉角曲線上極限彎矩下降20%所對應的轉角值[20]；θy為屈服轉角，其取值為理想雙線性模型上屈服彎矩對應的轉角值，理想雙線性模型彈性階段的直線斜率由真實曲線上0.6My的點確定。

2 優化約束條件

2.1 承載力和延性要求

冷彎型鋼達到極限承載力后，具有承載力及剛度退化的特征，因此在對圖1 中截面進行優化時，綜合考慮承載力-延性的條件：程欣[21]綜合實驗及數值分析結果發現，非塑性鉸截面的極限抗彎承載力并非都大于邊緣屈服彎矩，且延性大多在2～3，故要求非塑性鉸截面的承載力M 能夠超過邊緣屈服彎矩My，達到極限后仍有一定的非線性變形能力且承載力不發生急劇退化，使框架內力重分布變成可能；并將延性μ=3 作為延性類別的分界，認為μ<3 的構件變形能力較差，不能用于抗震設計。當μ>3 時，以保證構件在達到極限荷載后，可以繼續抵抗一定的荷載。所以本文優化的承載力和延性要求分別見式(2)和式(3)：

2.2 尺寸約束

本文旨在保證材料成本相當的情況下，即截面面積不變時，優化冷彎薄壁型鋼的截面尺寸，最大限度地提高其承載力和延性。因此，規定表1所示的兩種截面與圖3 所示的商業常用截面具有相同的材料和厚度，其厚度選取為1.5 mm，截面總長度為410 mm。需要注意的是，因為表1 中各變量需滿足截面總長度一定的限制條件，所以腹板高度不作為獨立設計變量。Ye 等[7]研究發現折疊翼緣截面內角為105°，外角為95°時結構承載力高，因此固定截面角度大小不變。其中，加勁都由兩個夾角為60°，邊長為10 mm 的肋組成。

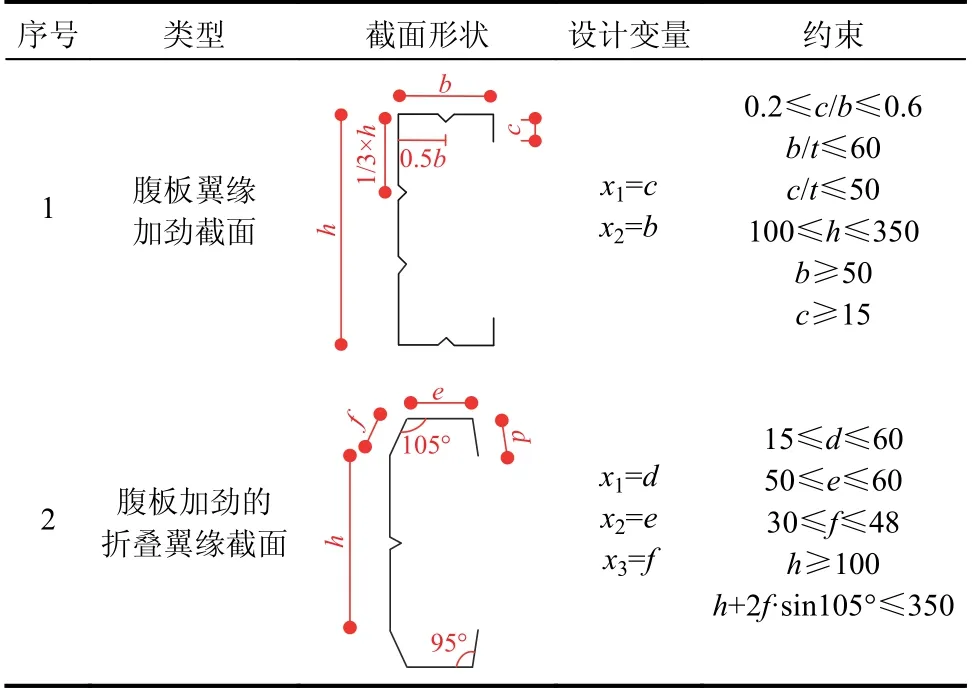
表 1 所選截面、設計變量和約束Table 1 Selected prototypes, design variables and constraints

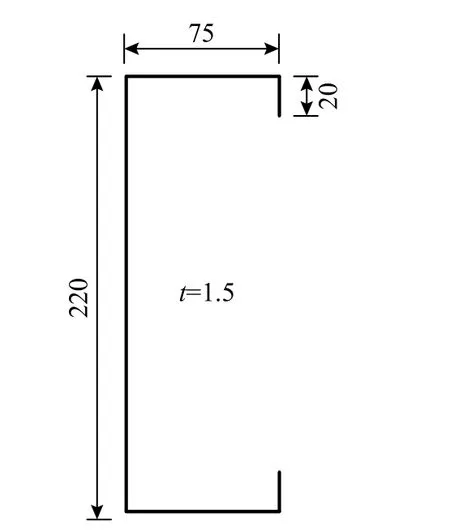
圖 3 商業常用截面尺寸 /mm Fig.3 Dimensions of commercial commonly used cross section

除了材料限制外，截面尺寸同時需滿足歐洲規范EN1993-1-3[22]中尺寸限值及制造約束，并考慮實際使用情況[7,15,23-24]。對于腹板翼緣加勁截面，根據EN1993-1-3[22]規范中的要求，需滿足0.2≤c/b≤0.6；為使樓板能和梁通過螺栓連接，平翼緣(截面1 中“b”及截面2 中“e”)最小寬度應為50 mm；因為過小的卷邊無法軋制或壓彎成型，所以卷邊(截面1 中“c”及截面2 中“d”)最小長度為15 mm；為便于與其他構件連接，腹板h 最小高度為100 mm；為控制樓板深度，截面深度最大為350 mm；為了給腹板留下足夠高度，對于截面2，折翼緣需控制為f≤48 mm。

3 優化框架

3.1 問題描述

鑒于成千上萬次的有限元計算，有限元模型被進一步簡化成單個槽鋼[15]，單元類型、材料、約束、邊界條件等都與1.1 節一致。從承載力和延性的角度出發，利用人工神經網絡和遺傳算法對表1 所示的兩種截面形式進行優化，優化過程如圖4 所示，其中M 是承載力，μ是延性，優化目標是使承載力和延性最大化，定義如下：

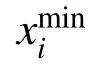
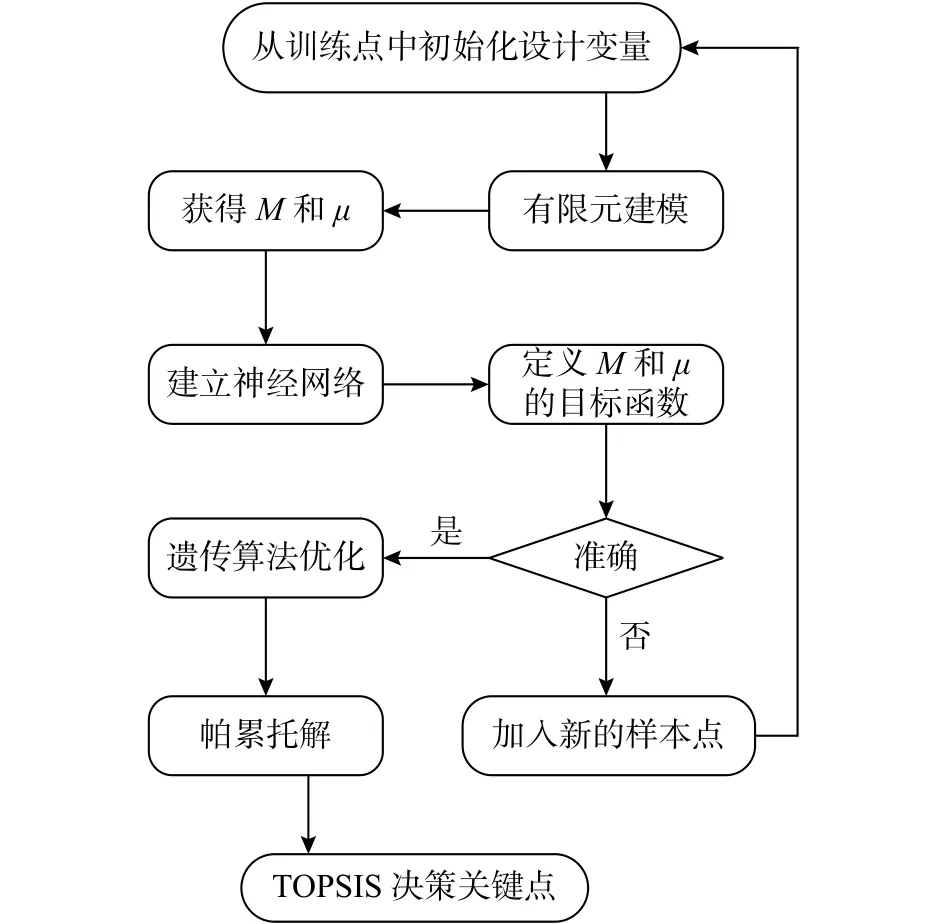
圖 4 優化流程圖Fig.4 Flowchart of the optimization process

首先，從表1 中給出的設計變量空間內任意選擇樣本點，ABAQUS 依據這些尺寸建模，在后處理模塊得到承載力M 和延性μ。其次，構建輸入(截面尺寸)和輸出(承載力、延性)的神經網絡，分別推導出承載力和延性的目標函數，如果這些函數響應是準確的，根據式(4)，利用遺傳算法最大化承載力和延性的目標函數以獲得一系列帕累托解，再用TOPSIS 決策出最優截面尺寸。否則，從表1 給出的設計變量空間中選擇新的樣本點，重復以上步驟，直至找到正確的最優解。

3.2 神經網絡

人工神經網絡是對人腦或生物神經網絡的抽象和模擬，分為輸入層、隱藏層、輸出層3 部分，每層神經元通過連接權重彼此聯系。通過合適的訓練步驟，人工神經網絡就能以一定的精度合理預測輸出值[25-26]。本文使用BP 算法，是目前應用最為廣泛的神經網絡模型之一。具體步驟如下：

首先，根據有限元建模結果準備數據。截面尺寸為輸入數據，M、μ為輸出數據，為了給本研究中的優化問題提供輸入輸出數據，從表1 中各截面尺寸的約束范圍內均勻選擇樣本點。在各變量設計空間內，每隔2 個單位取一個樣本，采用全因子設計，ABAQUS 依據這些樣本尺寸建模，得出M 和μ作為輸出數據。為了防止過擬合，這些樣本主要是用于訓練、測試、驗證3 個部分，70%的樣本用于網絡訓練，剩余30%用于測試，最后所有樣本都用于驗證網絡精度。

其次，構建合適的神經網絡。本文最終建立的神經網絡共有3 個隱藏層，隱藏層神經元個數依次是17、5、19，第1 層隱藏層激活函數采用S 型的對數函數，第2、3 層則采用雙曲正切函數，輸出層使用線性函數，每種截面有2×X 個神經網絡(承載力有X 個，延性有X 個)，X=17(第一個隱藏層神經元個數)×5(第二個隱藏層神經元個數)×19(第 三 個 隱 藏 層 神 經 元 個 數)×N(自 變 量個數)。

最后，使用均方誤差來驗證神經網絡的準確度，均方誤差的公式是：

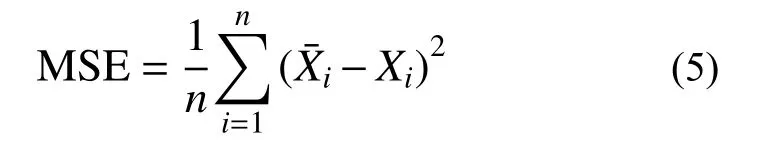
神經網絡擬合腹板翼緣加勁截面的承載力和延性曲面如圖5 所示，紅點代表被用于訓練的樣本，藍點代表被用于測試的樣本，紫色線段長度代表誤差大小。對于腹板翼緣加勁截面，承載力、延性誤差分別為0.21%、0.49%；對于腹板加勁折疊翼緣截面，承載力、延性誤差分別為1.38%、1.97%，結果表明所構造的神經網絡具有較高精度，可以用來預測冷彎薄壁型鋼的承載力和延性。

3.3 遺傳算法多目標優化

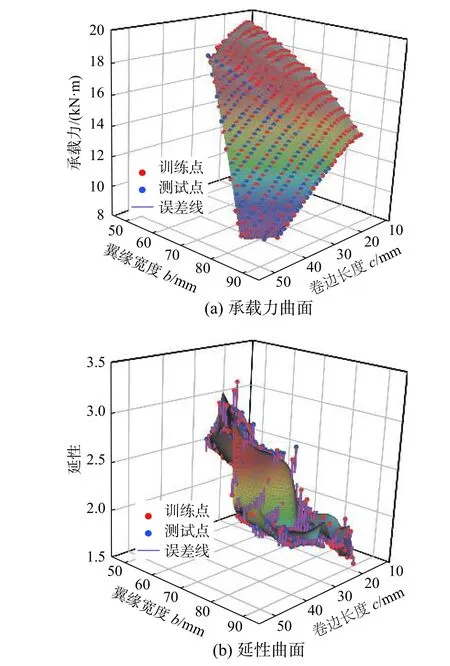
圖 5 神經網絡擬合腹板翼緣加勁截面的承載力和延性曲面Fig.5 The bearing capacity and ductility surface of channel with web and flange stiffeners fitted by the neural network

遺傳算法是一類借鑒生物界進化規律(適者生存、優勝劣汰)演化而來的隨機搜索算法，非常適用于處理復雜的非線性優化問題，易于并行化，魯棒性高[27-28]。該方法用適應度函數來評估個體，依據適應度值選擇個體，再對被選擇的個體進行交叉、變異操作，使種群中個體之間進行信息交換以得到新的個體，重復此類操作，種群不斷進化，直至滿足條件為止。遺傳算法中各參數設置如表2 所示。

表 2 遺傳算法參數Table 2 Parameters in genetic algorithm

3.2 節已闡述通過建立神經網絡尋找截面尺寸與承載力、延性的關系，用這種關系作遺傳算法中的適應度函數，為式(4)中定義的優化問題生成帕累托解(如圖6)。對于帕累托解，在改進任意目標的同時，至少會削弱一個其他目標的解，就存在目標之間相互沖突和無法比較的現象，因此再用TOPSIS 綜合評價方法找出帕累托解中的最優解。

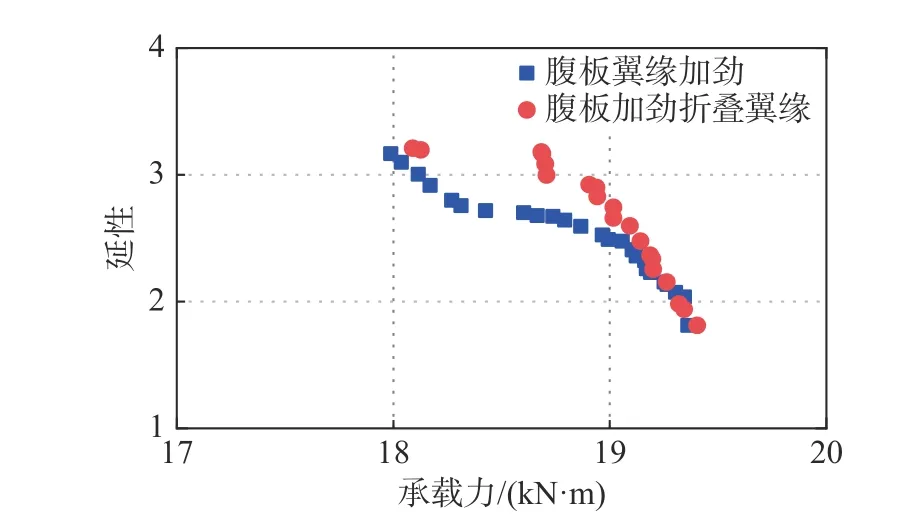
圖 6 帕累托解Fig.6 Pareto frontiers

TOPSIS 是從多個解決方案中決策出最優方案的常用方法。基于歸一化后的原始數據矩陣，給定每個目標的權重，構造規范化的加權決策矩陣，再分別定義每個目標的最優解與最劣解，決策問題的理想解即各目標最優解的合集，非理想解即最劣解合集，然后分別計算每個方案(帕累托解)與理想解和非理想解間的距離并排序，距理想解越近，而距非理想解越遠，則越優。

4 尋優結果與討論

4.1 尋優結果

圖5 已經給出了腹板翼緣加勁截面的承載力、延性隨幾何參數c 和b 的變化情況，如圖5(a)所示，增大c 或b，M 的值減小，由表3 也可知，當承載力最大時，腹板翼緣加勁截面c 和b 分別取EC3 規范規定的最小值15 mm 和50 mm，可以為腹板提供足夠高度；同樣，腹板加勁的折疊翼緣截面承載力最大時，d 和e 也取最小值。因此，對于這兩種截面，增加腹板高度可以提高承載力。很明顯增加腹板高度，則增加了截面慣性矩，故截面承載力提高。

腹板翼緣加勁截面的延性隨c 和b 變化情況如圖5(b)所示。當翼緣寬度b 較小時，延性出現峰值，隨著翼緣寬度增加，延性大致減小；由表3可知，腹板加勁的折疊翼緣截面延性最大時，平翼緣寬度e 也取較小值且折翼緣長度f 取EC3 要求的最大值48 mm，增大f 不僅可以加大截面深度，且控制了平翼緣寬度。因此，對于這兩種截面，當平翼緣寬度(腹板翼緣加勁截面中“b”及腹板加勁折疊翼緣截面中“e”)較小時，可以延緩畸變屈曲的發生，延性較大。而平翼緣寬度并非取最小值50 mm，是因為本文控制截面周長一定，若平翼緣取最小值，則腹板或卷邊長度較大，易發生局部屈曲導致延性降低。

表 3 承載力或延性最大值對應的截面尺寸Table 3 Cross-sectional dimensions corresponding to the maximum bearing capacity or ductility

依據表3 可知，當周長一定時，改變截面尺寸，冷彎薄壁型鋼承載力沒有太大變化，而延性變化較大，相比承載力，延性更為重要，因此根據各目標的重要性，本研究給定如下權重：WM=0.5 且Wμ=0.5，WM=0.4 且Wμ=0.6，WM=0.3 且Wμ=0.7，其中WM是承載力的權重，Wμ是延性的權重。不同權重下截面尺寸最優解見表4，對于不同的權重，最優解是相同的，而且是表3 中延性最大時的截面尺寸，足以見得延性的重要性。

為進一步考慮ANNs-GA 模型的精度，用ABAQUS 模擬了表4 中最優截面的構件(見表5)。對比表4 和表5，ABAQUS 計算得出的承載力、延性與ANNs-GA 預測結果的平均誤差在1%以下，表明本文使用的ANNs-GA 模型能夠較好的預測結構承載力及屈曲后行為。由表5 可知，腹板翼緣加勁截面、腹板加勁的折疊翼緣截面的承載力分別比商業常用截面高出22.33%、23.01%，延性分別高出213.73%、216.67%。可見對于1.5 mm的冷彎薄壁型鋼，設置加勁肋是非常有效的措施，加勁肋能夠有效地抑制截面失穩，導致峰值力矩略微增加，同時還能延遲和減輕屈曲導致的剛度退化，顯著增大結構的延性。此外，優化后的截面具有較小的翼緣寬度，進一步延緩了畸變屈曲的發生，所以優化后截面的延性比商用截面高出2 倍多。優化后的腹板加勁折疊翼緣截面的承載力和延性稍微大于腹板翼緣加勁截面，主要因為翼緣間相互支撐，彎曲剛度大，在折疊翼緣截面基礎上，腹板加勁也有助于解決翼緣腹板夾角過大對腹板支撐減弱的問題。通過簡單地優化截面尺寸，可以顯著提升結構性能，且優化后腹板翼緣加勁截面屈服強度為16.01 kN·m，承載力為18.02 kN·m，延性為3.2，腹板加勁的折疊翼緣截面屈服強度為17.8 kN·m，承載力為18.12 kN·m，延性為3.23，兩種最優截面滿足2.1 節中承載力大于屈服強度、延性大于3 的條件。

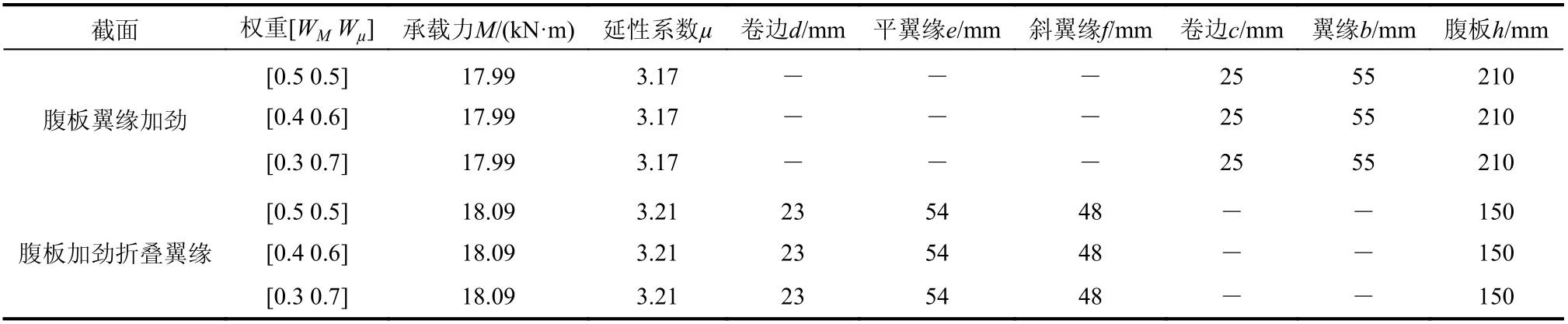
表 4 神經網絡-遺傳算法模型預測結構在不同優化方案下的最優解Table 4 Optimum solution of the structures predicted by ANNs-GA models for the different optimization scenarios

表 5 優化后截面與商用截面承載力、延性對比Table 5 Comparison of bearing capacity and ductility between the optimized sections and the commercial section

4.2 鋼材強度等級對結構性能影響

在表4 中兩種最優截面的有限元模型基礎上，改變冷彎薄壁型鋼強度等級，分別采用Q235、Q345 和Q420 鋼種，鋼材屈服強度和抗拉強度如表6 所示，其余參數與1.1 節有限元模型一致。分析鋼材強度等級對構件性能的影響，結果如表6和圖7 所示。由表6、圖7 可知，增大鋼材強度等級能夠顯著提高構件抗彎承載力，對延性影響較小。對于腹板翼緣加勁截面的構件，當鋼材強度等級從Q235 增大至Q345、Q420 時，其抗彎承載力分別增加40.4%和68.1%；對于腹板加勁的折疊翼緣截面，當鋼材強度等級從Q235 增大至Q345、Q420 時，抗彎承載力分別增加38.5%和62.9%。故鋼材強度等級對構件抗彎承載力影響較大。對于不同強度等級的鋼材，文中4.1 節所提2 種截面構件的抗彎承載力及延性隨尺寸變化的趨勢是相同的。

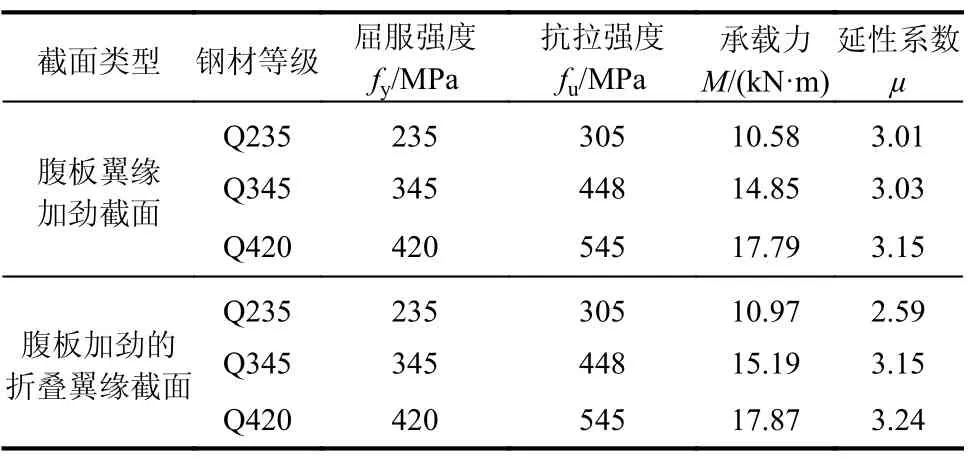
表 6 不同強度等級下有限元分析結果Table 6 FE analysis results of members with different steel grade

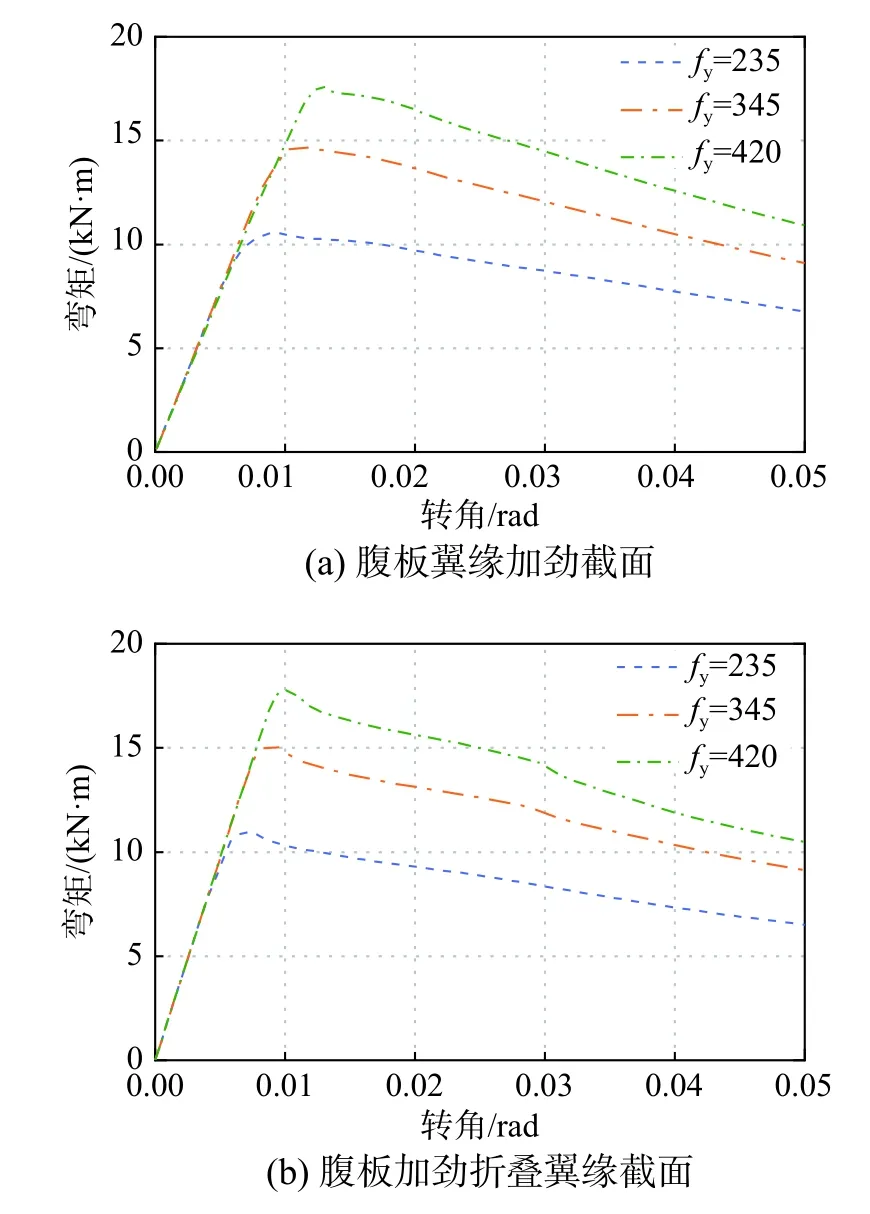
圖 7 不同鋼材強度等級下構件彎矩-轉角曲線對比Fig.7 Comparison of moment-rotation curves of members with different steel grade

4.3 截面參數控制

研究發現承載力、延性好的構件其破壞模式為畸變屈曲和固定端附近局部屈服，這說明控制構件的破壞模式基本上控制其承載力和延性的表現。為推廣冷彎型鋼的應用，可以采用設置加勁肋的措施防止腹板局部失穩，并通過控制截面尺寸防止翼緣失穩。同時，我們發現腹板翼緣加勁截面和腹板加勁的折疊翼緣截面的抗彎承載力都大于邊緣屈服彎矩，滿足式(2)要求。為了滿足式(3)的要求，在3.2 節所述的樣本中找出滿足μ=3 的截面尺寸臨界值。若樣本點不通過μ=3，則采用插值法確定μ=3 時的卷邊、翼緣尺寸，擬合出μ=3 時翼緣、卷邊相關關系表達式R、Q。結合表1中設計變量要求，得出兩種截面的優化設計式(6)和式(7)。當截面尺寸滿足式(6)和式(7)的要求時，則μ≥3。

對于腹板翼緣加勁截面，需滿足：

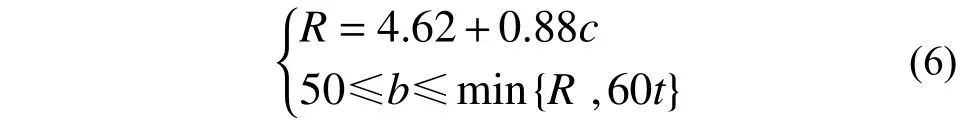
式中：R 為該截面翼緣寬度上限值。由4.1 節尋優結果可知，構件延性隨著翼緣寬度增加而減小，腹板翼緣加勁截面的翼緣取較小值時，構件延性最大。因此翼緣寬度b 需小于式(6)中臨界值R。由R 的計算公式可知，翼緣寬度最大限值隨卷邊長度c 增加而增大。根據優化結果，對于1.5 mm 厚的冷彎型鋼，建議該截面卷邊長度c 控制在25 mm～43 mm，隨著冷彎型鋼厚度增加，卷邊限值可適當放寬。

對于腹板加勁的折疊翼緣截面，需滿足：

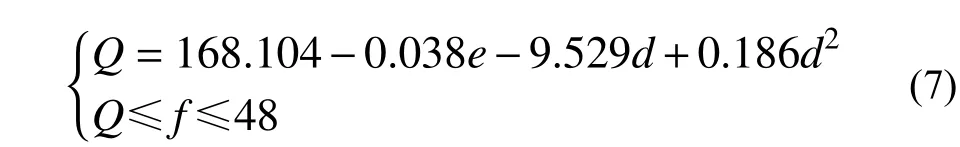
式中：Q 為該截面折翼緣長度下限值。由4.1 節尋優結果可知，構件延性隨折翼緣長度增加而增大，腹板加勁的折疊截面的折翼緣長度f 取最大值48 mm 時，構件延性最大。因此折翼緣長度f 需大于式(7)中臨界值Q。由Q 的計算式(7)可知，折翼緣長度的最小限值隨卷邊長度d 增加先減小后增大，受平翼緣寬度e 影響較小。根據優化結果，對于1.5 mm 厚的冷彎型鋼，建議該截面卷邊長度d 控制在23 mm～30 mm，隨著冷彎型鋼厚度增加，卷邊限值可適當放寬；平翼緣寬度e 滿足表1 要求，在50 mm～60 mm。

5 結論

本文對腹板翼緣加勁截面及腹板加勁折疊翼緣截面的承載力、延性進行了研究，這些指標對于冷彎型鋼的推廣應用至關重要。利用非線性有限元ABAQUS 建立了經試驗驗證的模型，獲得了單向彎曲下的承載力、延性；利用人工神經網絡和遺傳算法，考慮三種不同的情況的權重：WM=0.5 且Wμ=0.5，WM=0.4 且Wμ=0.6，WM=0.3 且Wμ=0.7，對這些截面尺寸進行優化，該方法預測誤差小于2%，可以準確預測冷彎型鋼的承載力及屈曲后行為。主要得出以下結論：

(1)提高鋼材強度等級能顯著增大構件的抗彎承載力，對延性影響不大。當截面面積和鋼材強度等級不變時，同一類型不同尺寸的截面，其承載力差別不大，而延性卻有較大差別，可見改變截面尺寸對提升延性性能至關重要。綜合考慮承載力、延性條件，在上述不同權重下，最優截面均為延性最大時對應的截面尺寸。

(2)對本文選定的腹板翼緣加勁截面和腹板加勁的折疊翼緣截面，增加腹板高度可提高承載力；采用較小的平翼緣寬度可以提高結構延性。此外，對于腹板加勁的折疊翼緣截面，延性最大時，折翼緣長度取最大值48 mm。文中給出了滿足所提出的承載力、延性條件下，兩種截面尺寸的優化設計公式。

(3)相同截面面積時，腹板加勁折疊翼緣截面的承載力、延性都優于腹板翼緣加勁截面，且前者優化后截面的承載力、延性比同等材料的商用截面分別高23.01%、216.67%，是較為理想的截面形式。

(4)對于厚度為1.5 mm 的冷彎薄壁型鋼，增加加勁肋既提高了極限承載力，又減輕了屈曲后剛度退化，可以大幅度提高延性，是非常有效的措施。