砂巖蠕變特性試驗(yàn)及三維非線性力學(xué)模型研究
劉凡熙,趙立財(cái),余建星,蔣騰健
(1. 廣西南寧水利電力設(shè)計(jì)院,廣西 南寧 530001;2. 天津大學(xué) 水利工程仿真與安全國(guó)家重點(diǎn)實(shí)驗(yàn)室,天津 300354;3. 南寧市城市建設(shè)投資發(fā)展有限責(zé)任公司,廣西 南寧 530031)
巖石是一種非均質(zhì)非線性的地質(zhì)材料,不僅具有彈性和塑性特征,其蠕變特征也是巖石力學(xué)中的核心研究?jī)?nèi)容之一[1]。水利水電工程、采礦工程、隧道工程中巖體蠕變變形明顯會(huì)對(duì)工程建設(shè)與運(yùn)營(yíng)造成威脅[2]。
對(duì)于巖石蠕變特性已有大量研究,江宗斌[3]探究水化學(xué)溶液和低溫對(duì)板巖蠕變特性的影響規(guī)律,基于此建立水化學(xué)-應(yīng)力-損傷耦合模型;徐鵬等[4]以粉砂巖為研究對(duì)象,開(kāi)展多級(jí)增量循環(huán)加卸載流變?cè)囼?yàn),根據(jù)試驗(yàn)結(jié)果提出一種可描述塑性應(yīng)變變化規(guī)律的裂隙塑性元件,與Burgers模型串聯(lián)從而得到一個(gè)新的蠕變模型;梁冰等[5]進(jìn)行片麻巖三軸壓縮蠕變?cè)囼?yàn),對(duì)其起始蠕變應(yīng)力閾值、長(zhǎng)期強(qiáng)度和加速蠕變啟動(dòng)時(shí)間進(jìn)行分析;何峰等[6]開(kāi)展不同含水率下的煤巖蠕變?cè)囼?yàn),研究水對(duì)煤巖蠕變變形、長(zhǎng)期強(qiáng)度等的影響。
目前關(guān)于砂巖蠕變特性試驗(yàn)所建本構(gòu)模型多為一維應(yīng)力狀態(tài)下的力學(xué)模型,難以反映巖石在三維應(yīng)力狀態(tài)下的蠕變行為。本文以某大型水利樞紐工程壩肩砂巖為研究對(duì)象,進(jìn)行差異性圍壓條件下的三軸壓縮蠕變?cè)囼?yàn)。重新定義了一個(gè)與時(shí)間和圍壓都相關(guān)的黏彈性模量E(p,t),并得到了新的三維非線性力學(xué)模型。
1 蠕變?cè)囼?yàn)
1.1 試驗(yàn)設(shè)備
蠕變?cè)囼?yàn)采用RLW-2000型巖石三軸流變?cè)囼?yàn)系統(tǒng)。該試驗(yàn)儀器由軸向、圍壓、孔壓加載系統(tǒng)進(jìn)行荷載控制,由伺服、控制系統(tǒng)進(jìn)行荷載和位移控制,通過(guò)數(shù)據(jù)采集和自動(dòng)繪圖系統(tǒng)進(jìn)行試驗(yàn)成果采集和輸出。軸向加載系統(tǒng)和圍壓加載系統(tǒng)的控制部分采用全數(shù)字伺服控制器,設(shè)備最大加載圍壓70 MPa,最大軸向荷載2000 kN。
1.2 試驗(yàn)材料及方案設(shè)計(jì)
本文研究背景為某大型水利樞紐工程壩肩邊坡,在滑帶附近取砂巖樣,將巖樣加工成直徑50 mm、高100 mm的圓柱樣,并打磨斷面使其平整。砂巖基本物理力學(xué)參數(shù)如表1所示。

表1 巖石基本物理力學(xué)參數(shù)Table 1 Basic mechanical parameters of rock
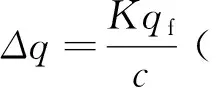
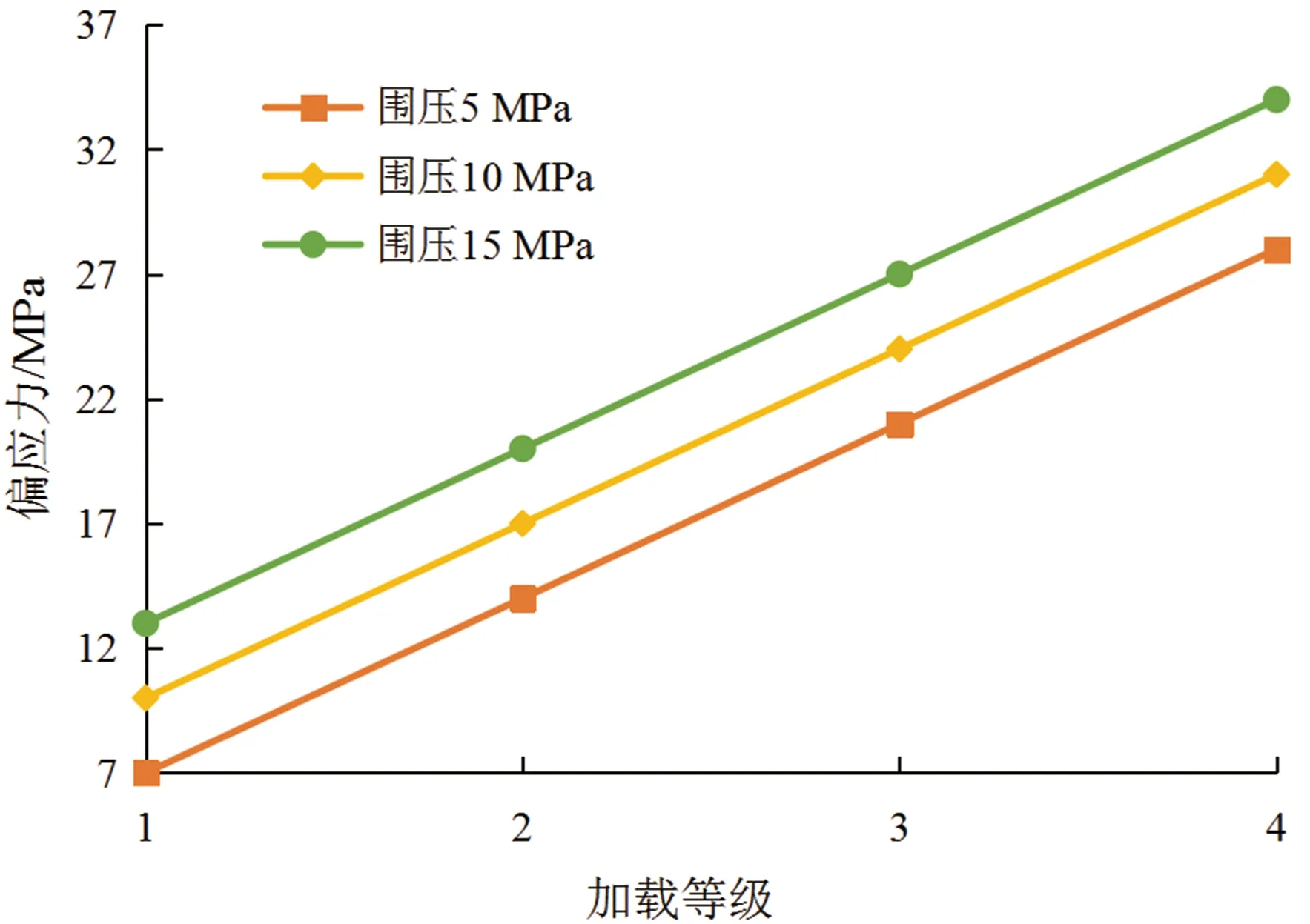
圖1 不同加載等級(jí)下的偏應(yīng)力設(shè)置圖Fig.1 Schematic diagram of deflection stress at different loading levels
1.3 試驗(yàn)結(jié)果
圖2為分級(jí)加載蠕變曲線,將每級(jí)軸向荷載(偏應(yīng)力)標(biāo)示在曲線上方。在圖2的基礎(chǔ)上利用玻爾茲曼線性疊加原理[7]可得到分別加載蠕變曲線,如圖3所示。
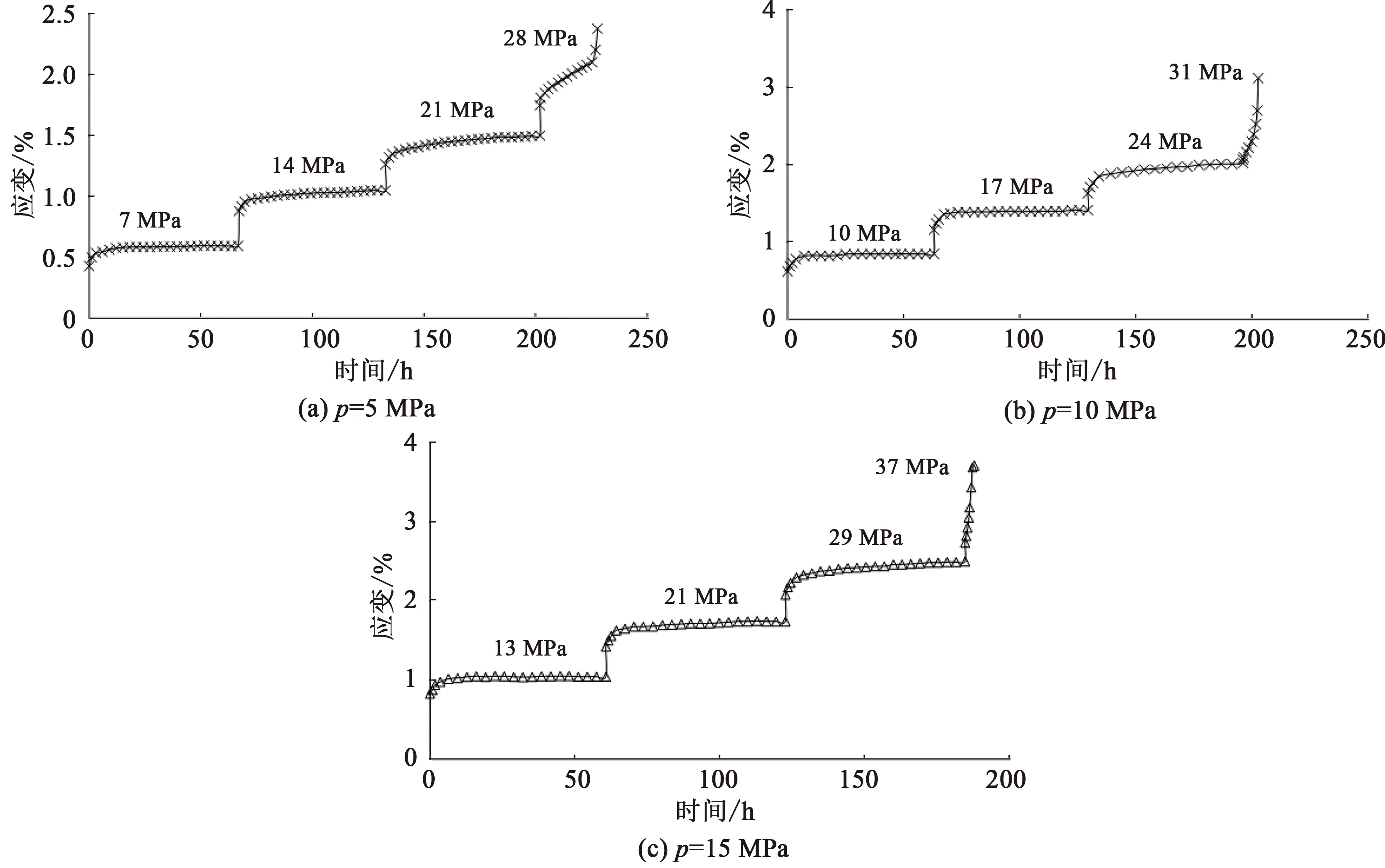
圖2 分級(jí)加載蠕變曲線Fig.2 Graded loading creep curves
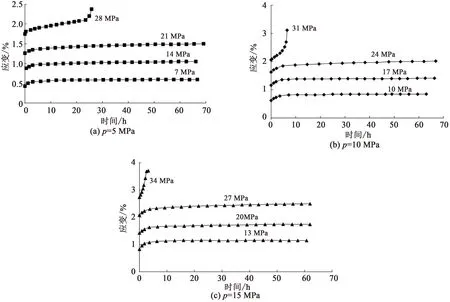
圖3 分別加載蠕變曲線Fig.3 Separate loading creep curves
根據(jù)圖2、3可作如下分析:
(1)巖石在軸向荷載下,首先產(chǎn)生一定量的瞬時(shí)彈性應(yīng)變,之后蠕應(yīng)變發(fā)展累積,蠕應(yīng)變量值遠(yuǎn)小于彈性應(yīng)變量值。當(dāng)偏應(yīng)力水平達(dá)到最后一級(jí)時(shí),巖石出現(xiàn)加速蠕變階段,蠕變速率急劇增長(zhǎng),在短時(shí)間內(nèi)屈服破壞。由此可知,巖石不僅表現(xiàn)有瞬時(shí)彈性階段、衰減和穩(wěn)定蠕變階段,達(dá)到破壞偏應(yīng)力水平后還表現(xiàn)有加速蠕變階段。
(2)在圍壓5 MPa~15 MPa下,巖石蠕變?cè)囼?yàn)歷時(shí)分別為228 h、203 h和188 h,破壞偏應(yīng)力水平持續(xù)時(shí)間分別為25.81 h、6.49 h和3.24 h,蠕變?cè)囼?yàn)總歷時(shí)和破壞偏應(yīng)力水平持續(xù)時(shí)間隨著圍壓的增大而遞減。
2 試驗(yàn)結(jié)果
2.1 蠕變速率
研究巖石蠕變速率的變化規(guī)律,可以更好地認(rèn)識(shí)蠕變變形發(fā)展過(guò)程。張春陽(yáng)等[8]提出如下蠕變速率解析方法:
(1)
式中:Δti為蠕變時(shí)間;ε1,ε2,…,εn為各微段蠕變;Δε1,Δε2,…,Δεn為微段蠕變之差;Δε和vi表示Δti時(shí)間內(nèi)總應(yīng)變和平均應(yīng)變速率。
根據(jù)式(1)的方法繪制蠕變速率曲線,如圖4所示,限于篇幅,僅給出圍壓5 MPa下的蠕變速率曲線。
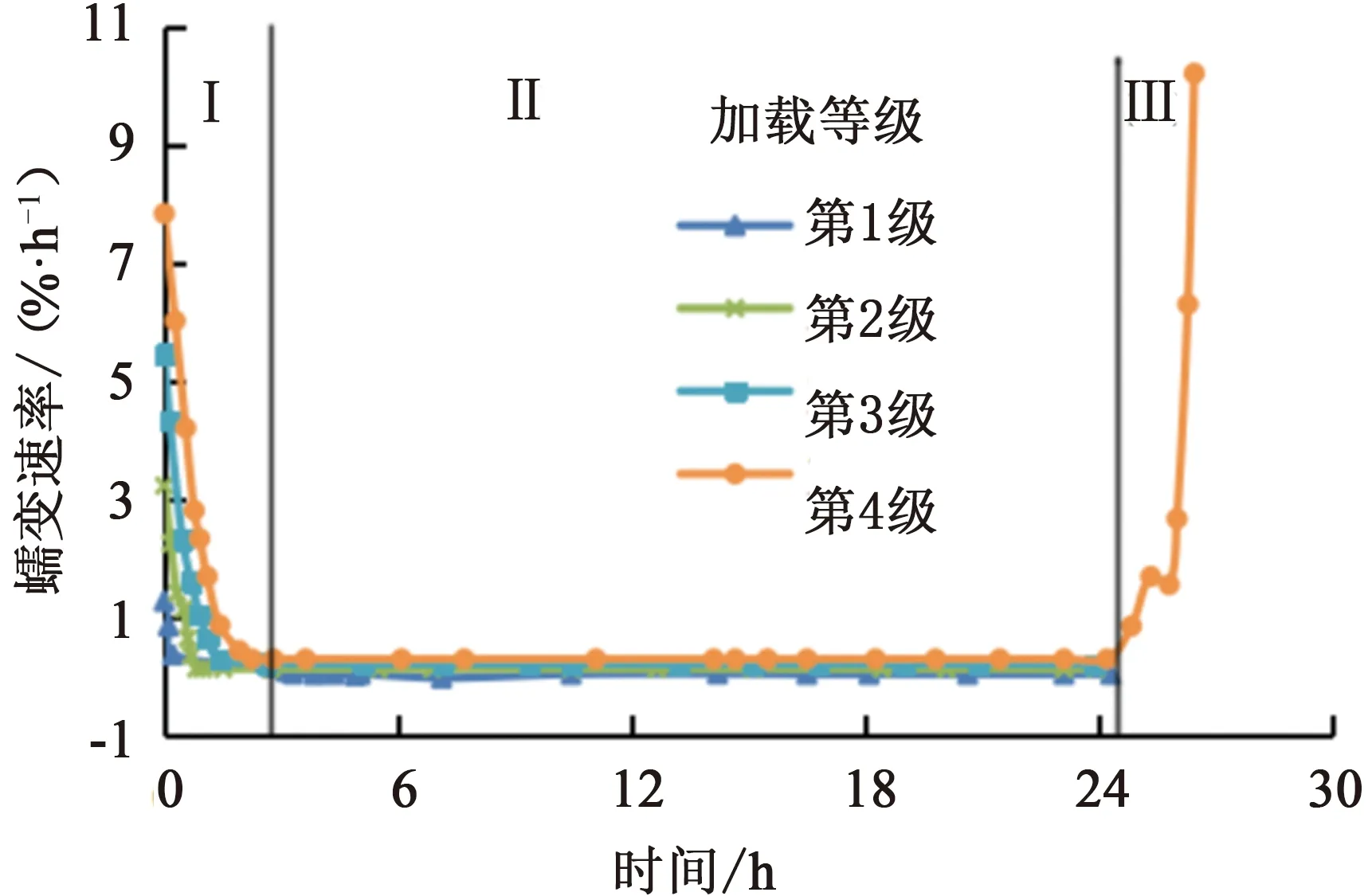
圖4 蠕變速率曲線Fig.4 Creep-rate curves
由圖4可看出,巖石第4級(jí)蠕變加載曲線呈“桶”形,曲線簇從左到右分為3個(gè)區(qū)域:衰減蠕變階段、穩(wěn)定蠕變階段和加速蠕變階段。其中巖石第1~4級(jí)加載等級(jí)下的衰減蠕變階段,對(duì)應(yīng)圖中區(qū)域Ⅰ,該階段的蠕變速率在同一加載等級(jí)下逐漸遞減,在同一時(shí)刻隨著加載等級(jí)的提高而遞增;穩(wěn)定蠕變階段對(duì)應(yīng)圖中區(qū)域Ⅱ,該階段的蠕變速率在同一加載等級(jí)下基本保持恒定,在同一時(shí)刻隨著加載等級(jí)的提高而遞增;加速蠕變階段對(duì)應(yīng)圖中區(qū)域Ⅲ,蠕變速率劇增,短時(shí)間內(nèi)達(dá)到極限值。
2.2 穩(wěn)態(tài)蠕變速率與偏應(yīng)力的關(guān)系
繪制不同圍壓不同加載等級(jí)下的巖石穩(wěn)態(tài)蠕變速率與偏應(yīng)力的關(guān)系曲線,如圖5所示。
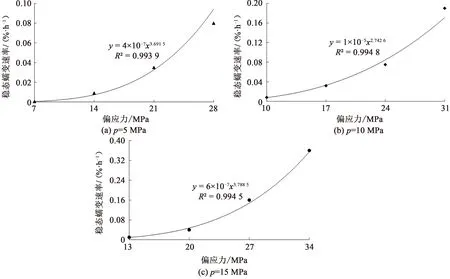
圖5 穩(wěn)態(tài)蠕變速率與應(yīng)力水平關(guān)系曲線Fig.5 Curves of the relationship between steady creep rate and stress level
由圖5可知,3種圍壓下的穩(wěn)態(tài)蠕變速率與偏應(yīng)力皆呈冪函數(shù)關(guān)系,R2分別為0.993 9、0.994 8和0.994 5。在巖石的穩(wěn)定蠕變階段,雖然穩(wěn)態(tài)蠕變速率與圍壓呈冪函數(shù)增長(zhǎng)關(guān)系,但穩(wěn)態(tài)蠕變速率變化范圍較小,相對(duì)比較恒定,由此說(shuō)明該階段是巖石微裂紋不斷發(fā)育和擴(kuò)展的過(guò)程,巖石蠕變?nèi)^(guò)程皆處于微裂紋發(fā)育、延展直至貫通的活動(dòng)狀態(tài)。
2.3 等時(shí)應(yīng)力-應(yīng)變關(guān)系
選取圖3中1 、11、21、31、41、51、61 h共7個(gè)時(shí)間節(jié)點(diǎn)的偏應(yīng)力-應(yīng)變數(shù)據(jù),繪制成等時(shí)蠕變曲線簇,如圖6所示。李良權(quán)等[9]取該曲線簇的拐點(diǎn)為巖石長(zhǎng)期強(qiáng)度。
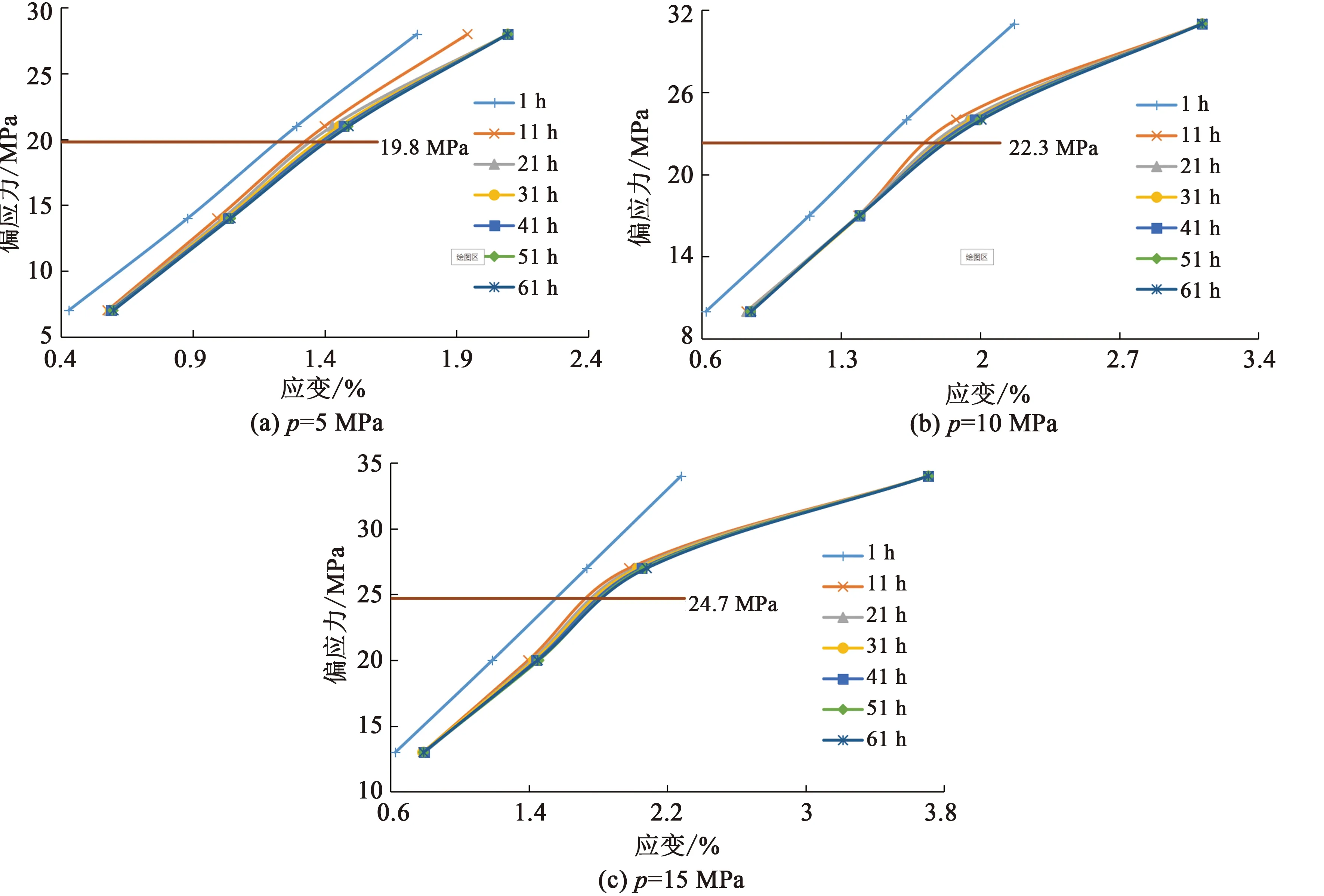
圖6 等時(shí)蠕變曲線簇Fig.6 Isometric creep-curve clusters
由圖6可知,通過(guò)取拐點(diǎn)的方法,圍壓5 MPa、10 MPa和15 MPa下的長(zhǎng)期強(qiáng)度分別為19.8 MPa、22.3 MPa和24.7 MPa,長(zhǎng)期強(qiáng)度隨圍壓的增強(qiáng)而逐漸增大。隨著時(shí)間增長(zhǎng),等時(shí)蠕變曲線簇逐漸偏于橫軸,表現(xiàn)出明顯的非線性特征。當(dāng)巖石未進(jìn)入加速蠕變階段時(shí),蠕變變形為黏彈性變形,對(duì)應(yīng)圖6中曲線簇的近線性段,于是將等時(shí)應(yīng)力-應(yīng)變曲線的斜率定義為黏彈性模量E(p)。圖7為黏彈性模量與不同圍壓的關(guān)系曲線。
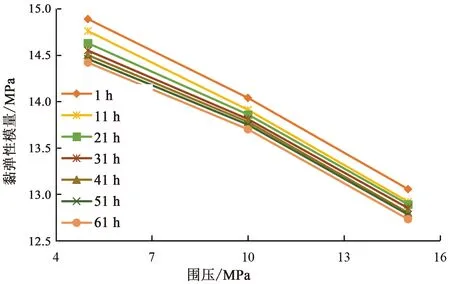
圖7 黏彈性模量與圍壓關(guān)系曲線Fig.7 Relationship between viscoelastic modulus and confining pressure
由圖7可發(fā)現(xiàn)曲線近線性,用式(2)對(duì)圖7中7條曲線進(jìn)行線性回歸,結(jié)果如表2所示。
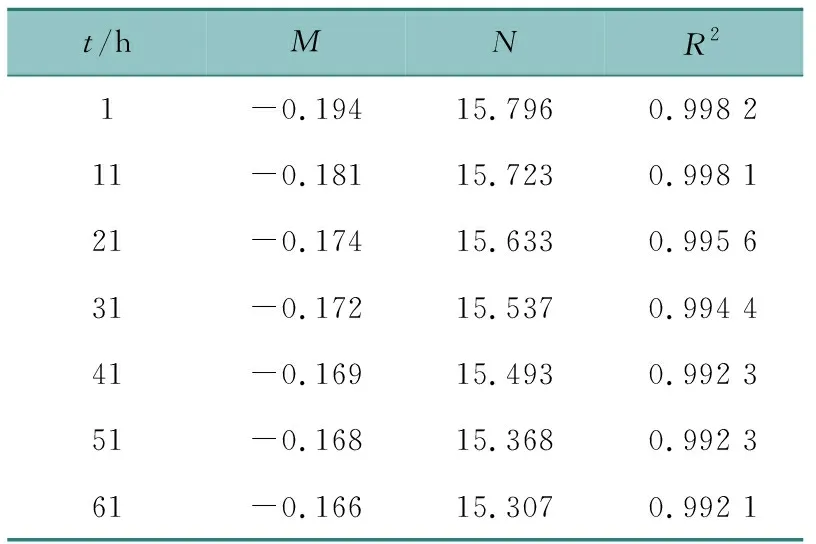
E(p)=Mp+N。 (2)
由表2可知,R2平均值為0.994 7,E(p)的兩個(gè)參數(shù)M、N的變化在某種意義上可反映砂巖蠕變的非線性特征,圖8為M、N隨時(shí)間變化的數(shù)據(jù)分布。

圖8 M和N擬合Fig.8 Fitting of M and N
從圖8可看出,M值與時(shí)間t呈冪函數(shù)關(guān)系,N值與時(shí)間t線性相關(guān)。式(3)、(4)分別為M、N的擬合結(jié)果:
M=-at-b,
(3)
N=-ct+d。
(4)
將式(3)、(4)代入式(2)得
E(p,t)=-at-bp-ct+d。
(5)
式(5)即為本文所建可反映差異性圍壓條件的黏彈性模量,通過(guò)式(5)可建立砂巖受時(shí)間和圍壓影響的時(shí)效力學(xué)響應(yīng)過(guò)程。
3 三維蠕變力學(xué)模型
3.1 模型建立
元件模型具有結(jié)構(gòu)簡(jiǎn)單、便于應(yīng)用的特點(diǎn),但常用的傳統(tǒng)元件模型如西原模型、Burgers模型等,其本構(gòu)方程為線性狀態(tài),難以描述巖石蠕變的非線性特征。故本文在傳統(tǒng)Burgers模型的基礎(chǔ)上,串聯(lián)一個(gè)非線性黏塑性元件[10],從而得到六元件模型。假定其中Kelvin體中的彈性體服從式(5),從而得到一個(gè)新的非線性蠕變力學(xué)模型。模型示意圖如圖9所示。
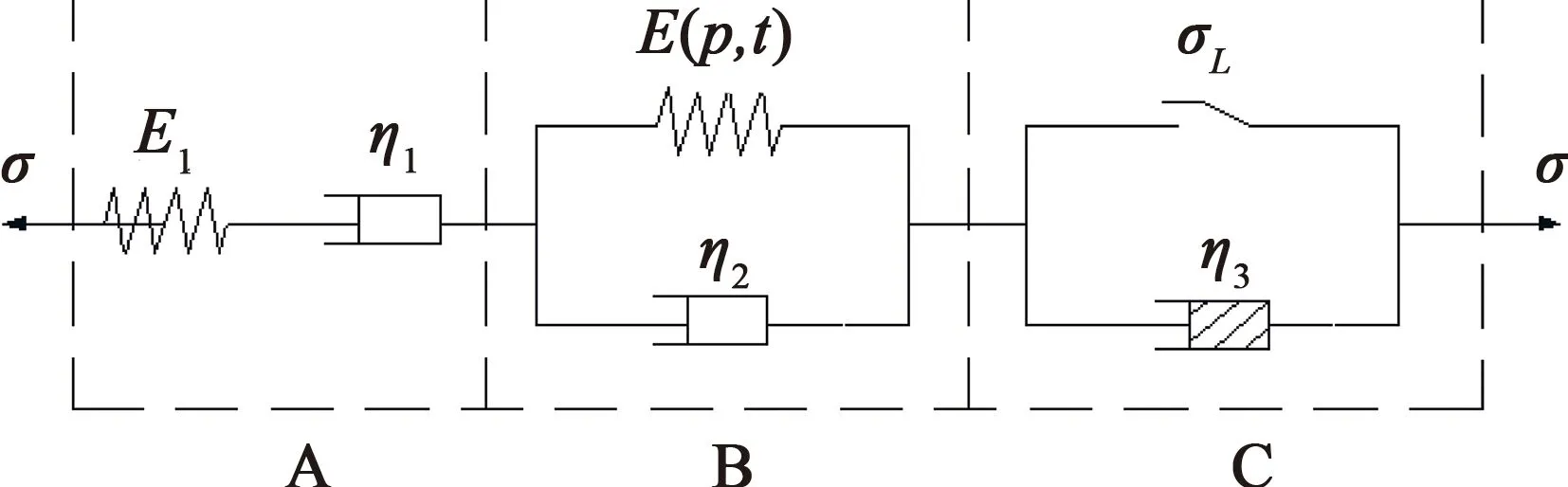
圖9 模型示意圖Fig.9 Illustration of the model
當(dāng)σ0<σL時(shí),非線性黏塑性體失效,其狀態(tài)方程為:
(6)
式中,σ0為初始應(yīng)力,σA、εA、E1和η1分別為圖10模型A部分的應(yīng)力、應(yīng)變、彈性模量和黏滯系數(shù),σB、εB、E(p,t)和η2分別為模型B部分的應(yīng)力、應(yīng)變、黏彈性模量和黏滯系數(shù)。相應(yīng)的蠕變方程為:
多年來(lái),何王廟故道一直是周邊40萬(wàn)人口、200多戶漁民、80萬(wàn)畝農(nóng)田的水源地。為給江豚提供一個(gè)舒適的生存環(huán)境,監(jiān)利縣對(duì)保護(hù)區(qū)水域的漁業(yè)捕撈、網(wǎng)箱養(yǎng)殖、洲灘放牧和農(nóng)業(yè)污水排放等方面進(jìn)行了綜合治理,并贖買(mǎi)了核心區(qū)漁民的捕撈工具,杜絕核心區(qū)捕撈活動(dòng)。
(7)
當(dāng)σ0≥σL時(shí),非線性黏塑性體發(fā)揮作用,相應(yīng)的狀態(tài)方程為:
(8)
式中,σC、εC和η3分別為模型C部分的應(yīng)力、應(yīng)變和黏滯系數(shù),σL為長(zhǎng)期強(qiáng)度。相應(yīng)的蠕變方程為:
(9)
式(7)、(9)即為本文所建非線性蠕變力學(xué)一維模型。
假設(shè)巖石為各向同性體,根據(jù)廣義Hooke定律,三維應(yīng)力狀態(tài)下的本構(gòu)關(guān)系為
(10)
式中,σm為球應(yīng)力張量,Sij為偏應(yīng)力張量,K為體積模量,G為剪切模量。
由于在巖體工程中,巖石多處于三維應(yīng)力狀態(tài),而本文巖石蠕變?cè)囼?yàn)也是三軸壓縮應(yīng)力路徑,故而有必要建立三維力學(xué)模型。假設(shè)巖石為各向同性體,分解巖石內(nèi)部的應(yīng)力張量,于是有
σij=Sij+δijσm,
(11)
一般認(rèn)為,σm只改變物體體積,Sij只引起形狀變化,因此也可以將應(yīng)變張量分解為
εij=eij+δijεm,
(12)
式中,εij為應(yīng)變張量,εm為球應(yīng)變張量,eij為偏應(yīng)變張量。
為了簡(jiǎn)化問(wèn)題,假定巖石材料蠕變僅由偏應(yīng)力張量引起,與體積變化無(wú)關(guān),將式(7)、(9)推廣為三維情形
(13)
式中,(Sij)0為初始偏應(yīng)力張量,(Sij)L為對(duì)應(yīng)長(zhǎng)期強(qiáng)度的偏應(yīng)力張量。
在本文三軸壓縮蠕變?cè)囼?yàn)中,中間主應(yīng)力σ2=p,于是
σm=(σ1+2p)/3,
(14)
再結(jié)合式(11),則有
S11=2(σ1-p)/3,
(15)
將式(5)、(15)代入式(13)可得
(16)
式(16)即為本文所建的新的三維非線性蠕變力學(xué)模型的軸向蠕變方程。
3.2 模型參數(shù)識(shí)別及驗(yàn)證
新建三維蠕變模型中有G1、η1、η2、η3、a、b、c、d、(σ1-p)L等共9個(gè)參數(shù)。圖7取拐點(diǎn)的方法可確定巖石長(zhǎng)期強(qiáng)度σL,由于σL是通過(guò)等時(shí)偏應(yīng)力-應(yīng)變關(guān)系求解而得,所以偏應(yīng)力(σ1-p)L在數(shù)值上等于σL,通過(guò)廣義Hooke定律可求解G1。另外7個(gè)參數(shù)通過(guò)數(shù)學(xué)軟件1stOpt,基于爬山算法(Hill Climbing)求解。圖10為識(shí)別結(jié)果與圖3試驗(yàn)數(shù)據(jù)對(duì)比曲線,表3為模型參數(shù)。
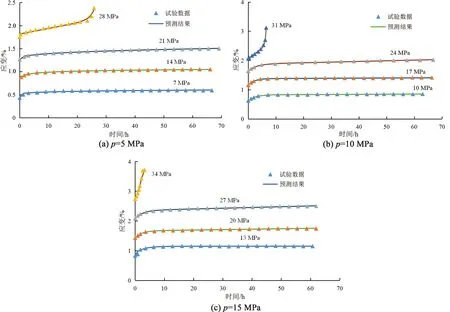
圖10 試驗(yàn)數(shù)據(jù)與預(yù)測(cè)結(jié)果對(duì)比曲線Fig.10 Comparison curves between test data and predicted results
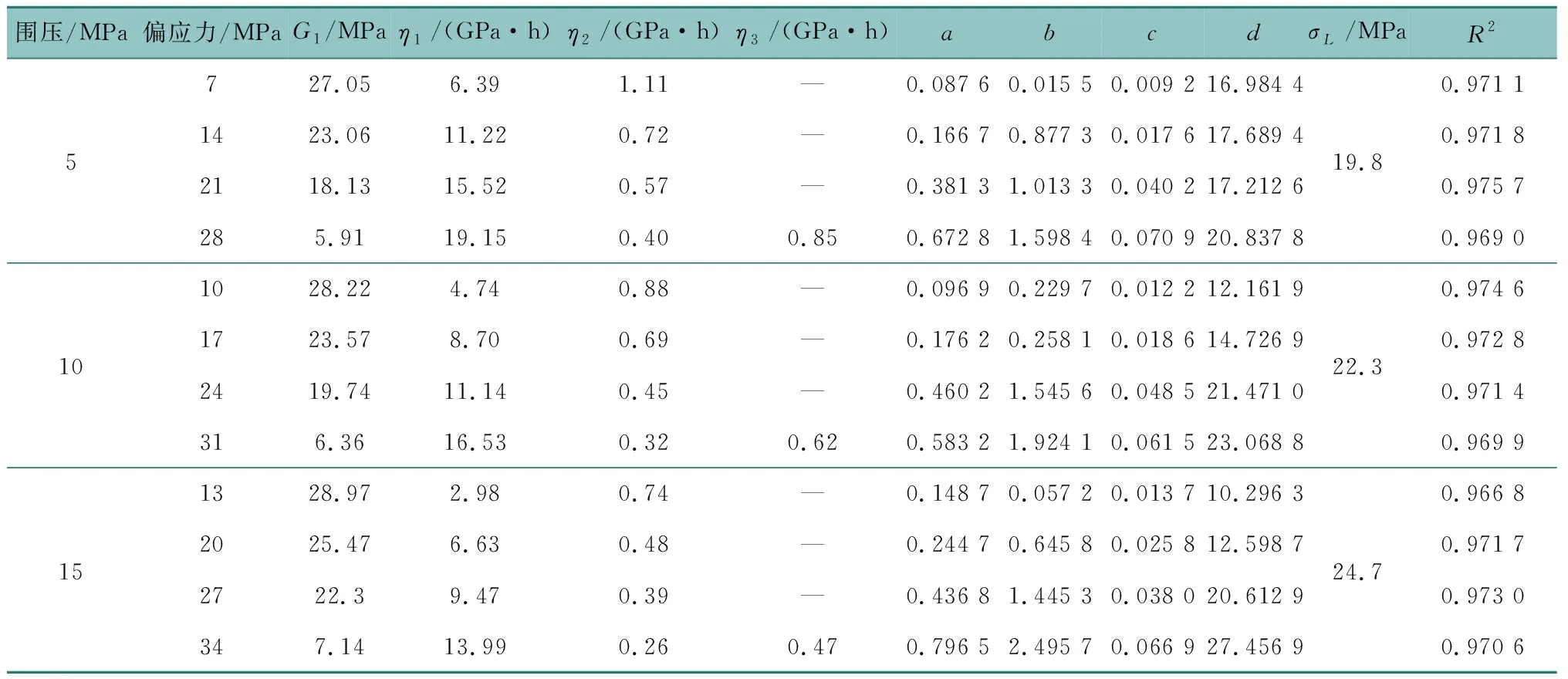
表3 蠕變力學(xué)模型參數(shù)
由圖10和表3可看出,本文新建三維非線性蠕變力學(xué)模型具有良好的識(shí)別效果,R2平均值為0.971 5,能較為準(zhǔn)確地描述砂巖在三維應(yīng)力狀態(tài)下的蠕變力學(xué)行為。砂巖在不同應(yīng)力狀態(tài)下,加速蠕變階段具有不同的曲線特征,新建三維模型仍具有較強(qiáng)的識(shí)別能力,由此證明本文所建模型的合理性和適用性。
4 結(jié)論
(1)巖石穩(wěn)態(tài)蠕變速率與圍壓呈冪函數(shù)增長(zhǎng)關(guān)系,穩(wěn)定蠕變階段是巖石微裂紋不斷發(fā)育和擴(kuò)展的過(guò)程,巖石蠕變?nèi)^(guò)程皆處于微裂紋發(fā)育、延展直至貫通的活動(dòng)狀態(tài)。
(2)通過(guò)等時(shí)蠕變曲線簇取拐點(diǎn),得到砂巖在圍壓5 MPa、10 MPa和15 MPa下的長(zhǎng)期強(qiáng)度分別為19.8 MPa、22.3 MPa和24.7 MPa,長(zhǎng)期強(qiáng)度與圍壓大小呈正相關(guān)。砂巖的長(zhǎng)期強(qiáng)度折減較大,實(shí)際工程應(yīng)用中應(yīng)考慮其折減問(wèn)題。
(3)本文通過(guò)研究砂巖蠕變的非線性特征,定義了與圍壓相關(guān)的黏彈性模量E(p),經(jīng)過(guò)推導(dǎo)變換得到了可反映巖石蠕變受時(shí)間和圍壓影響的E(p,t)。在傳統(tǒng)Burgers模型的基礎(chǔ)上,串聯(lián)一個(gè)非線性黏塑性元件,并將E(p,t)應(yīng)用到模型中,得到一個(gè)新的一維蠕變力學(xué)模型。將其拓展到三維應(yīng)力狀態(tài),進(jìn)行模型辨識(shí),證明新建三維非線性蠕變力學(xué)模型描述砂巖在不同三維應(yīng)力狀態(tài)的可行性和合理性。

