培養數學建模思想 增強數學關鍵能力

>>>董紀華

新高考承載著促進立德樹人、考查學生關鍵能力和學科核心素養、助力人才選拔與培養等多重功能。縱觀近幾年高考數學試題，已經從只對數學知識進行考查，轉向對數學能力、數學素養的考查。“數學建模”作為新課標提出的六大核心素養之一，成為近幾年高考的考查熱點，我們有必要從課程標準出發研究高考試題，提升關鍵能力。

一、從新課標看數學建模

數學建模就是對現實問題進行數學抽象，用數學語言表達問題、用數學方法構建模型解決問題的素養。《普通高中數學課程標準(2017年版)》提出了六個數學學科核心素養，即數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析;設置了函數、幾何與代數、統計與概率、數學建模活動與數學探究活動四條主線;提出了“三會”，即“會用數學眼光觀察世界，會用數學思維思考世界，會用數學語言表達世界”，其中，用數學語言表達世界，就是運用數學知識、數學方法構建數學模型，解決客觀世界中現實問題的能力素養。可見，在學習的過程中，我們除了要重視“四基”“四能”，也要重視數學與客觀世界的聯系，通過數學建模活動獲得數學建模思想，活學活用數學知識，培養數學核心素養。

二、從高考評價看數學建模

《中國高考評價體系說明》指出，高考評價應基于學科核心素養確定考查的關鍵能力與必備知識。近年來，高考評價越來越注重數學的應用性，高考試題通過設置真實問題情境，創設開放性、可探究的問題，考查考生的數學能力。數學建模作為數學內容的主線，不僅要求同學們掌握扎實的數學知識，更要求同學們增強知識間的聯系。有邏輯地運用數學知識技能解決實際問題，成為近年高考考查的趨勢。高考試題將數學建模活動與數學探究活動融入考查之中，同學們雖然不能在考場上真正進行數學建模活動，但可以應用數學建模思想解決問題，將實際問題抽象為數學問題，靈活運用已有的數學知識構建數學模型，用數學的方式解決實際問題。

三、例析高考中的數學建模與數學模型

例1.(2020年全國卷Ⅲ,理科4題)Logistic模型是常用數學模型之一,可應用于流行病學領城.有學者根據公布數據建立了某地區新冠肺炎累計確診病例數I(t)(t的單位：天)的Logistic模型其中K為最大確診病例數.當I(t★)=0.95K時,標志著已初步遏制疫情,則 t★約為(ln19≈3)

A.60 B.63 C.66 D.69

模型分析：本題以新冠肺炎為實際背景，引入Logistic模型揭示某地區新冠肺炎累計確診病例數隨天數的變化規律，充分體現了函數是刻畫變量間變化規律的數學模型。同學們應深入理解指數型函數模型蘊含的規律特征，利用已有的函數知識，結合函數與方程的基本思想，通過對數學問題的計算，預測疫情得以遏制的規律，解決實際問題，感悟函數的預測功能。

例2.(2020年全國卷Ⅲ,理科18題)某學生興趣小組隨機調查了某市100天中每天的空氣質量等級和當天到某公園鍛煉的人次,整理數據得到下表(單位：天)：

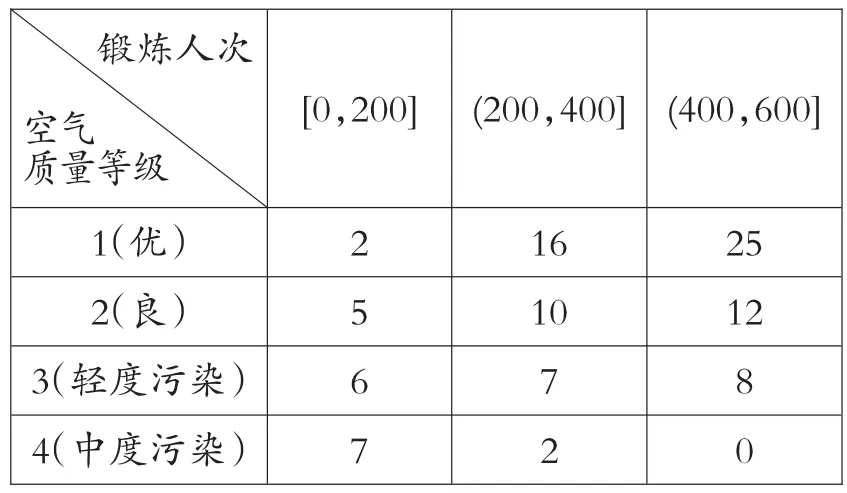
鍛煉人次空氣質量等級［0,200］ (200,400］ (400,600］1(優) 2 16 25 2(良) 5 10 12 3(輕度污染) 6 7 8 4(中度污染) 7 2 0

(1)分別估計該市一天的空氣質量等級為1,2,3,4的概率;

(2)求一天中到該公園鍛煉的平均人次的估計值(同一組中的數據用該組區間的中點值為代表);

(3)若某天的空氣質量等級為1或2,則稱這天“空氣質量好”;若某天的空氣質量等級為3或4,則稱這天“空氣質量不好”.根據所給數據,完成下面的2×2列聯表,并根據列聯表,判斷是否有95%的把握認為一天中到該公園鍛煉的人次與該市當天的空氣質量有關?

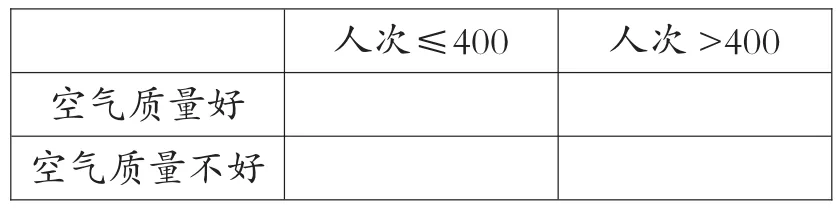
人次≤400 人次＞400空氣質量好空氣質量不好

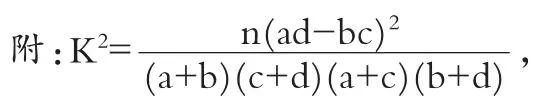
P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828

解析：(1)由頻數分布表可知,該市一天的空氣質量等級為1的概率為=0.43,等級為2的概率為=0.27,等級為 3的概率為=0.21,等級為4的概率為=0.09.

(2)由頻數分布表可知,一天中到該公園鍛煉的人次平均數為=350.

(3)2×2列聯表如下：

人次≤400 人次＞400空氣質量不好 33 37空氣質量好 22 8

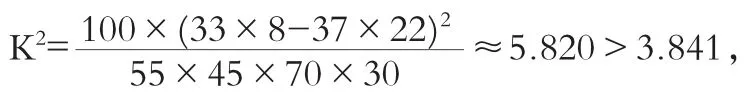
因此，有95%的把握認為一天中到該公園鍛煉的人次與該市當天的空氣質量有關。

模型分析：本題以空氣質量問題和公園鍛煉人數的聯系為背景，考查了概率統計模型。在歷年高考試題中，概率統計問題通常都十分注重生產生活實際與數學知識方法的聯系。現實世界中存在著很多隨機現象，不確定性中又蘊含了一定的規律。我們須從大量的統計數據中分析、識別這些規律.高考試題對概率統計模型的考查，需要考生從大量文字和數據中提取關鍵信息，選擇恰當的統計圖表(如列聯表、頻率統計表、直方圖、折線圖等)整理數據，并確定關鍵的數字特征，反映總體特征，有時還需要檢驗模型并改進模型。同學們應該在復習中深入理解統計基本思想、熟練掌握統計基本模型，運用統計學基本方法獲取、分析、整理數據，選擇或建立恰當的概率統計模型，通過計算解決實際問題。

四、提高數學建模素養的一些建議

1.夯實基礎，掌握數學模型

在構建數學模型時，我們需要對已學數學知識的本質特征有較為深刻的認識，理解與掌握數學模型的本質。如函數是刻畫變量間變化規律的數學模型，概率是研究隨機現象的數學模型，統計模型和統計工具往往可以幫助我們理解和處理數據，并與概率相聯系研究不確定現象等，這樣才能將錯綜復雜的現實問題與數學模型建立聯系。在求解數學模型時，我們須用數學的方法和基本思想，進行邏輯推理與準確計算，如對函數性質的討論、對方程的求解、應用數列的性質解決問題等。在檢驗和改進數學模型時，往往需要我們對數學解釋有足夠的認識，如用概率統計學知識進行風險決策，對人們的生產生活給出指導。如果模型與現實問題產生了較大的誤差，我們需要根據數學專業知識檢驗所得結果的科學性，并改進模型。這些都需要我們夯實基礎，理解每一個數學概念的本質，弄清楚定理的來龍去脈，提高數學運算能力。

2.關注知識的聯系性與整體性

從高考試題的角度來看，我們會發現與數學建模思想有關的試題，考查的知識點往往并不固定，有時問題涉及的知識內容也不是單一的，綜合性較強。另外，從數學學習的角度來看，我們要弄清楚構成某一個數學研究對象的要素之間的關系，以及不同研究對象之間的關系。數學知識之間總是以數學的邏輯有機、連貫地聯系在一起，我們只有將數學看成一個整體，復習時注重知識間的聯系，如等式與不等式的關系、函數與方程的關系、幾何與代數的關系、結構與形式的關系等等，才能在綜合性較強的數學建模問題中提出問題、分析問題、解決問題。

3.重視對問題背景的分析

近幾年高考中與數學建模相關的題目，都以真實情境為背景，具有科學性、時效性、廣泛性的特點，題目情境多種多樣。例如在2020年高考中，許多地方的高考試題都加入了以“新冠肺炎”為背景的問題，也有空氣質量、信息熵等實際背景。這些試題往往有大量的文字描述，還會有一些科學性、時效性較強的術語，同學們在復習中應注意對該類問題的訓練，通過對材料的閱讀、分析，感受問題的本質，體驗從現實問題中抽象出數學問題的思維，與此同時，加深對數學知識的理解與應用。