柔性中壓直流配電網的新型電流差動保護方案

劉 靜， 呂 睿

(中國礦業大學(北京)機電與信息工程學院， 北京 100083)

近年來，化石能源短缺以及環境污染問題日益突出，世界各國越來越重視可再生能源的開發利用，比如光伏、風電。伴隨著配電網中分布式可再生能源的大量接入，再加上風電、光伏等可再生能源發電的波動性，導致潮流均衡協調控制愈發復雜，如何保證含分布式能源配電網的安全可靠已然成了一大難題[1]。而基于模塊化多電平換流器(modular multilevel converter, MMC)的柔性中壓直流配電網被認為是一種解決分布式能源接入問題的有效技術方案[2-3]。

對于多電平換流器并網的直流配電網，故障電流上升快且不存過零點，換流站中的絕緣柵雙極型晶體管(insulated gate bipolar translator，IGBT)等電力電子期間受到電流沖擊時極易發生損壞，這對直流配電網的繼電保護系統提出了極高的要求[4-5]。現有的直流系統主要利用行波保護作為主保護，但是其在發生高阻故障、電壓變化很小時的可靠性不高，需要利用電流差動保護作為后備保護[6]。目前應用的電流差動保護，由于受到故障初期分布電容電流的干擾，保護會先延時一段時間，此后的保護裝置動作本身就需要500 ms左右的延時，這意味著即使保護能夠正確動作，從發生故障到保護裝置動作也需要大約1 s的延時[7-8]。這段延時可能會導致故障電流上升到較大值，而觸發換流站處的保護，導致在電流差動保護動作前換流站就已經閉鎖，擴大故障停電范圍。

為了避免這個問題，中外學者已經進行了相關研究。這些研究的主要目標都是減少保護所需的延時，按照方式不同可以分為兩類：減少通信所需的延時和減少躲過分布電容電流所需的延時。文獻[9-10]利用磁環作為線路邊界設計了基于單端電氣量來設計保護判據，直接消除了收集線路兩端信息所需的時間，但這類方法的可靠性還有待實踐檢驗。而對于直流配電線路，線路長度相對較短，通信所需的延時較少，因此可以直接通過改良傳統電流差動保護來提高可靠性。文獻[11-12]以架空線路為研究對象，基于貝瑞隆線路模型，通過極模轉換采用不同的方法計算差動電流。這種方法忽略了線路的頻變特性，導致在極對地故障時會出現健康極的誤跳。對于架空線路來說，頻變特性的影響較小，這種方法有一定的可行性，然而對于柔性中壓直流配電網來說，多用電纜作為傳輸線，電力電纜的結構特點和敷設環境決定了它的電容效應和頻變效應，相較于架空線路會更加明顯。對于電容效應，由于電力電纜的幾何參數很小且絕緣層的介電常數很大，因此其電容效應比架空線路明顯得多[13]，使得電力電纜中的分布電容電流更大。而對于頻變效應來說，一方面，電力電纜內部分層的多導體結構加深了集膚效應[14]對截面電流分布的影響；另一方面，電力電纜大多與土壤直接接觸使得大地返回效應更加明顯。這樣，在短路故障暫態，不同頻率的電流波在線路上傳播時就會具有不同的傳播速度和衰減速度，使得頻變效應更加明顯。因此，之前忽略線路頻變效應的方法就不再適用，亟需研究能夠適用于電纜線路的電流差動保護方法。

目前，部分學者提出了一些適用于電纜線路的電流差動保護方法。文獻[15]基于頻變線路模型，對所得到的測量信號在2 ms的時間窗內進行時頻域轉換來計算差動電流，有效消除了分布電容電流的影響，但計算時間較長；文獻[16]中提出了一種基于補償點電流作為判據來補償分布式電容電流影響的電流差動保護方案，同時在頻域上推導了考慮頻率特性傳輸線上的電壓與電流計算公式;文獻[17]基于輸電線路等傳遞過程理論(equal transfer process of transmission lines, ETPTL)，同一低通濾波器對線路兩端的電壓、電流信號進行足夠低的截止頻率處理后，可以將線路上的電壓分布視為線性分布，通過對線性分布電壓的積分，計算并補償分布電容電流，改進傳統的電流差動保護。但是，這些方法均需要較大的計算量，對運算速度提出了較高的要求。

基于上述問題，如何減小乃至消除電力電纜線路頻變效應和分布電容電流對電流差動保護的影響，并且保護動作快速可靠，成了柔性直流配電網電流差動保護的關鍵研究點。現針對含電纜線路的柔性中壓直流配電網，提出一種基于貝瑞隆模型的新型電流差動保護方案，可消除分布電容電流的影響，其計算方法簡單且可靠性高，最后驗證了該方案提高電流差動保護速動性的有效性。

1 基于貝瑞隆模型的新型電流差動保護方案

1.1 貝瑞隆模型

貝瑞隆模型利用行波理論，用行波的觀點分析電磁波在線路的傳播過程來解釋暫態過程[18]，將線路近似成無損傳輸線，是最簡單的分布參數模型，它反映了內部無故障的線路兩端電壓與電流之間的關系，如圖1所示。

圖1 單根無損線路貝瑞隆等效模型Fig.1 Bergeron equivalent model for single lossless circuit

貝瑞隆域形式為

(1)

式(1)中：uj(t)、ij(t)和uk(t)、ik(t)分別為j端和k端的電壓、電流在t時刻的測量值；Zc為線路波阻抗；Ijk(t-τ)和Ikj(t-τ)分別為線路兩端的等效電流源，計算公式為

(2)

式(2)中：τ為電磁波通過線路全長所需的時間。

在實際情況中由于需要考慮損耗，可以采用分段的思想將線路作為集中電阻串入無損線路中，可以得到考慮損耗線路貝瑞隆模型的時域形式為

(3)

式(3)中：Z=Zc+R/4為考慮損耗后的等效波阻抗。

令h=(Zc-R/4)/(Zc+R/4)，R為線路全長等效電阻。

(4)

1.2 基于貝瑞隆模型的新型電流差動保護原理

由前文可知，造成常規電流差動保護性能較差的原因是分布電容電流的影響和電力電纜頻變特性的影響。而貝瑞隆模型是一種線路分布參數模型，是消除分布電容電流影響并提高電流差動保護性能的一種有效方法。根據前文推導的單根無損線路的貝瑞隆模型，式(1)可變形為

(5)

線路內部發生故障時單根無損線路如圖2所示。

圖2 發生內部故障時的單根無損線路Fig.2 Single lossless circuit in case of internal failure

將式(5)分別應用于j與故障點f、f與k之間的線路，通過t和t-τj相互代替消去uf(t)可得

(6)

式(6)中：τj為電磁波從j端傳播到f點所需的時間。由無損線路的貝瑞隆模型可知，j端通過貝瑞隆模型計算得到的計算電流icj(t)為

(7)

因此，式(6)可以寫為

ij(t)-icj(t)=if(t-τj)

(8)

由式(8)可知，有內部故障發生于無損線路中時，線路j端實際電流與線路j端通過貝瑞隆模型計算得到的電流之差為故障電流。由于實際線路存在損耗，應采用考慮線路損耗的貝瑞隆模型獲得參考點的計算電流，即

(9)

式(9)中：R0為單位長度線路電阻；x為線路j到故障點f的距離；v為波速。

因此，可以在線路上任選一個參考點m。分別通過測量保護安裝處j端k端和的電壓、電流uj、ij和uk、ik，利用式(9)計算參考點m左側和右側的電流icjm和ickm，二者并非此處的實際電流，而僅為計算電流。當沒有區內故障發生時，線路相當于一段貝瑞隆模型等效線路，此時從j端計算的m點左側故障電流icjm和從k端計算的m點右側故障電流ickm相等；而線路發生區內故障時，線路不再是一段貝瑞隆模型等效線路，而是j-m和m-k兩段，此時從j端計算的m點左側故障電流icjm和從k端計算的m點右側故障電流ickm的差值波形可以很好地反映故障電流的波形。由以上討論的電流差動保護方法，可以構造判據，即

(10)

式(10)中：idiff是利用線路兩端保護安裝處的電壓電流采樣值通過貝瑞隆模型計算得到的參考點m兩側的差電流；iset是電流差動保護的電流閾值，可以采取如下方法來確定：首先確定最大不平衡電流，主要包括各種區外故障時可能出現的不平衡電流和區內不對稱故障時非故障極的不平衡電流。然后，將最大不平衡電流與可靠系數相乘，即可得到電流閾值。這樣，基于貝瑞隆模型的電流差動保護在原理上已經考慮了分布電容電流的影響，因此在應用中不再需要通過延時來躲過分布電容電流的影響，可以有效地改進常規電流差動保護動作時間較長的問題。

2 算例仿真及分析

為驗證所提的基于貝瑞隆模型的新型電流差動保護的有效性和優越性，在PSCAD/ ETMDC上搭建了偽雙極±20 kV的中壓雙端直流配電系統，其中傳輸線為直流電纜，線路n-j和線路j-k的長度均為10 km，換流站均為模塊化多電平換流站，取線路j-k中點為參考點m，如圖3所示，其中Bus為母線。

圖3 ±20 kV中壓三端直流配電系統Fig.3 ±20 kV medium voltage three-terminal DC distribution system

2.1 常規電流差動保護

要保證直流系統的差動保護能夠正確可靠動作，必須保證其能夠正確區分最嚴重的區外故障和故障電流最小的區內故障之間的差別。對于直流雙極系統，故障電流最小的區內故障為區內高阻接地故障，故障電流最大的區外故障為區外近端金屬性接地故障。而對于直流偽雙極系統，發生接地故障時的故障電流很小，考慮區內雙極高阻短路故障和區外近端雙極金屬性短路故障。

系統啟動后0.6 s時分別在k端右側和距離j端3 km處分別引入雙極金屬性短路故障和雙極高阻短路故障，對于j-k線路的電流差動保護分別對應區外故障和區內故障，研究其差動電流的故障暫態特性，如圖4所示。

圖4 區內故障和區外故障的暫態差動電流Fig.4 Transient differential current for in-zone and out-of-zone faults

由圖4可以看出，區內高阻故障時，在故障暫態階段計算得到的差動電流與實際故障電流的暫態波形有較大的出入，且最大值在0.25 kA左右。而區外近端金屬性故障時的差動電流有最大值，且在0.4 kA左右的波動。很顯然，此時常規電流差動保護無法正確區分區內雙極高阻短路故障和區外近端雙極金屬性短路故障，需要設置延時來躲過電流交叉部分。這種電流的波動實際上是由線路分布電容電流和直流電纜線路的頻變特性共同作用產生的。

2.2 基于貝瑞隆模型的新型電流差動保護

為驗證以上所述的基于貝瑞隆模型的新型電流差動保護方案對于提高電流差動保護速動性的有效性，根據前文介紹的電流差動保護方案，分別在區內雙極高阻短路故障和區外近端雙極金屬性短路故障時的差動電流特性，并與常規的電流差動保護方案進行對比。兩種保護方案的故障暫態差動電流曲線如圖5所示。

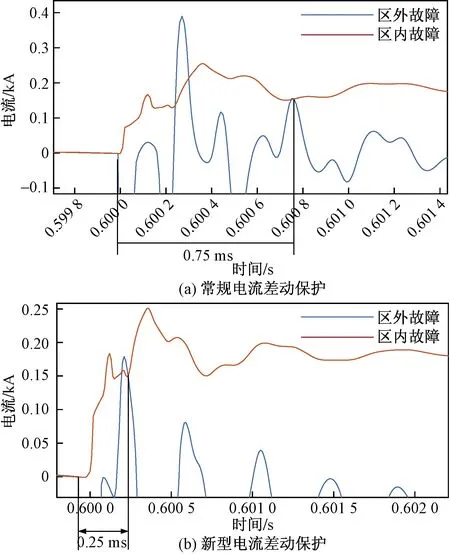
圖5 兩種電流差動保護故障暫態差動電流對比Fig.5 Comparison of transient differential current between two current differential protection faults

由圖5(a)可知，區外近端雙極金屬性短路故障時的差動電流與區內雙極高阻短路故障時的差動電流存在兩次交叉，這樣就需要延時來躲過這兩次交叉，再判斷是否發生故障，這段延時約為0.75 ms。而對于圖5(b)所示的新型電流差動保護，區外近端雙極金屬性短路故障時的差動電流與區內雙極高阻短路故障時的差動電流只存在一次交叉，因此只需要延時0.25 ms。這樣，使用這種新型電流差動保護可以縮短近2/3的延時，有效提高了電流差動保護的速動性。

3 結論

由于中壓直流配電網存在短路電流上升快且無自然過零點、IGBT等元件耐過流能力又極差的問題，同時電纜線路的頻變效應和分布電容電流加劇了柔性中壓直流配電網電流差動保護性能不佳的問題，針對柔性中壓直流配電網的電流差動保護展開研究，并通過實例仿真，得到以下結論：

(1)線路分布電容電流和直流電纜線路的頻變效應會導致常規電流差動保護無法正確區分區內雙極高阻短路故障和區外近端雙極金屬性短路故障。表明常規電流差動保護無法適用于柔性中壓直流配電網。

(2)針對電纜線路的特點，計及分布電容電流的影響，提出基于貝瑞隆模型的新型電流差動保護方案，保護動作準確快速，相比于常規電流差動保護，延時縮短2/3，極大地提高了柔性中壓直流配電網電流差動保護的速動性。