函數等高線的妙用

江西省吉安市白鷺洲中學 (343000) 尹丙武

我們知道，地理中“等高線”指地形圖上高程相等的相鄰各點所連成的閉合曲線.借助于這一名詞,數學中對于函數y=f(x),若存在互不相等的實數a,b,c,使f(a)=f(b)=f(c)=t,則y=t稱作函數y=f(x)的等高線.利用函數的等高線求解與交點橫坐標有關式子的取值范圍問題綜合性較強,難度也較大,一般作為客觀題壓軸題出現.本文就此類問題的破解方法予以總結.

1.利用對稱性求解等高線對應的交點橫坐標之和

x3+x4的取值范圍是( ).

A.(2，5] B.(-∞，0]∪[5,+∞)

C.[5,+∞) D.(2,+∞)

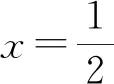
圖1

評注：本題關鍵用兩次對稱性，由性質“若A(x1,y1),B(x2,y2)關于直線x=a對稱，則x1+x2=2a”得出其中兩個交點橫坐標之和為常數x1+x2=1，另兩交點橫坐標之和x3+x4=2m.再結合圖像確定m≥2，由此以m為主元，求出m的取值范圍.

2.利用對稱性求解等高線對應的交點橫坐標之積

A.(18,28) B.(18,25) C.(20,25) D.(21,24)

解析：不妨設a

圖2

評注：本題關鍵用兩次對稱性，由性質“若直線y=m與函數y=|logax|(a>0且a≠1)有兩個不同交點A(x1,y1),B(x2,y2),則|logax1|=|logax2|，所以-logax1=logax2，x1x2=1.”得出其中兩個交點橫坐標之積為常數，即ab=1；另兩交點橫坐標之和為常數，即c+d=10.再結合圖像確定3

3.求等高線對應的交點橫坐標函數的取值范圍

圖3

評注：本題關鍵是以m為主元，把所求式子中的變量a，b，c均用m表示，由此將所求的多元代數式轉化成一元，再利用函數的性質求解.