基于收斂思維的變式教學實踐與思考
——以解析幾何復習課為例

福建省莆田第二中學 (351131) 盧 妮 謝曉瓊

一、問題的提出

收斂思維就是思維主體把從不同渠道得到的各種信息聚合起來，重新加以組織，使之明確無誤地指向一個(或一種)選擇.多題歸一實際上就是收斂思維.在無邊高考數(shù)學解析幾何復習過程中，對于“形異質(zhì)同”的問題，教師需要深刻地挖掘其本質(zhì)，以本質(zhì)為核心統(tǒng)領(lǐng)這些問題，跳出題海，來到“變式”的岸，才能讓學生在考試中面對不同的問題情境時立于不敗之地.變式教學中如何幫助學生從變化多端的“形”，抓住不變的“質(zhì)”呢？本文就基于收斂思維的的變式教學結(jié)合高考數(shù)學解析幾何復習課的課堂教學實踐案例談?wù)勔稽c自己的想法.

二、教學案例

“問渠哪得清如許,為有源頭活水來”,高考題目源于教材，又高于教材，因此高三復習課有必要回歸教材,選取有代表性、重點突出的典型問題，有意識地進行一題多變訓練，引導學生從變化的問題形式中找出不變的規(guī)律，發(fā)展學生分析問題和解決問題的能力.

1.回歸教材

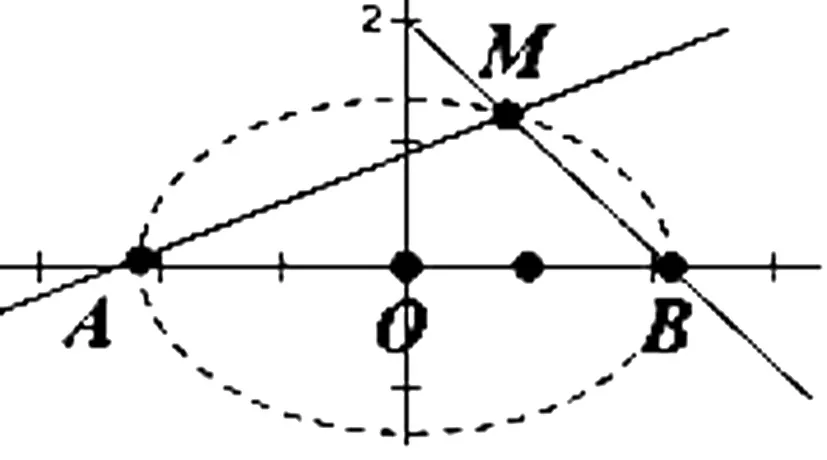
圖1

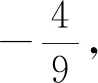
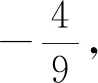
點評：這是一道典型的求軌跡方程.條件涉及動直線的斜率是定值,對題目適當?shù)淖兪骄涂梢宰兂龈嗟念愃祁}目.

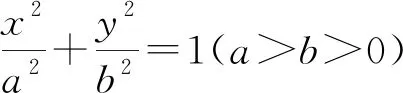
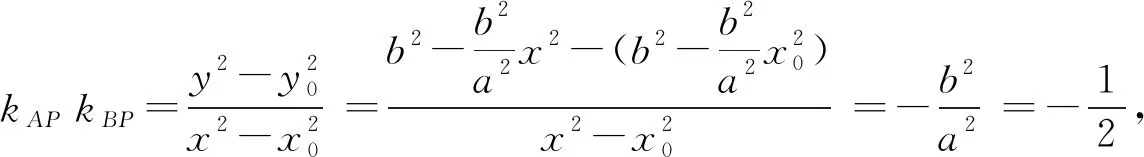
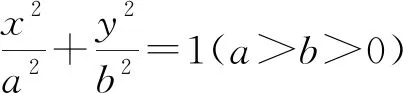
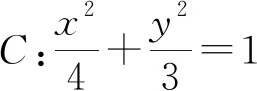
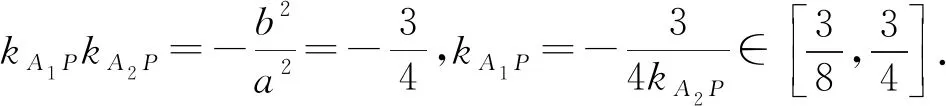
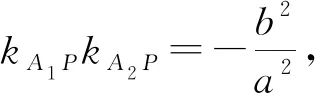
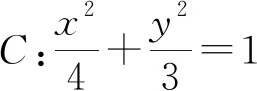
分析：由結(jié)論1,A,B兩點關(guān)于原點對稱，即直線AB過定點(0,0).

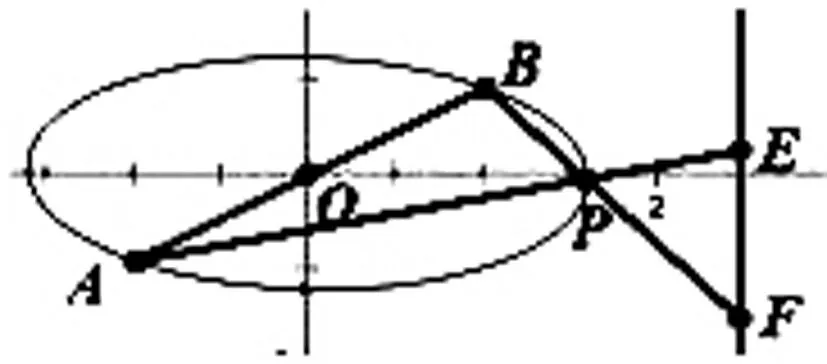
圖2

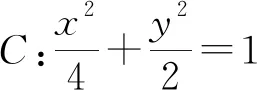
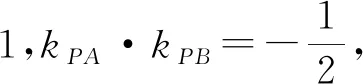
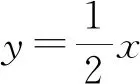
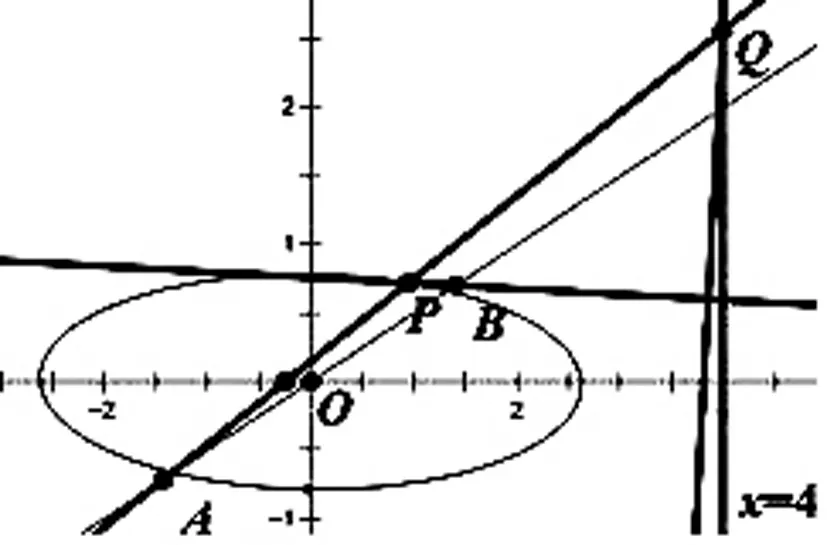
圖3

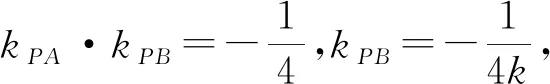
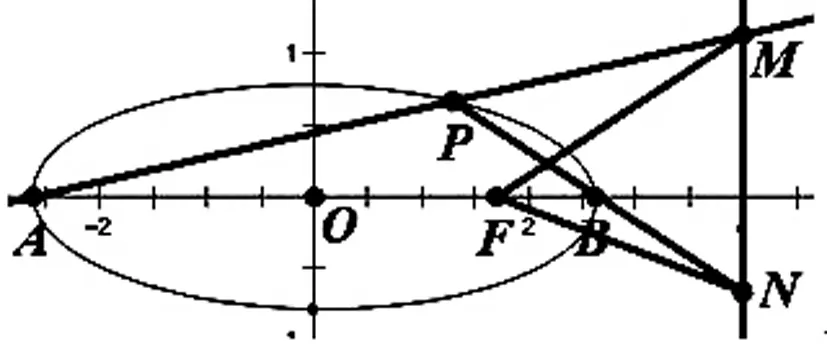
圖4

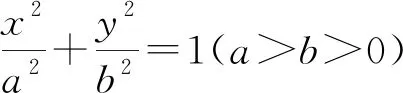
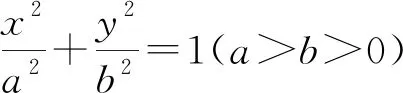
2.聚焦高考

案例2 (2015年全國卷理科Ⅱ卷第20題)已知橢圓C:9x2+y2=m2(m>0),直線l不過原點O且不平行于坐標軸，l與C有兩個交點A，B，線段AB的中點為M.

(Ⅰ)證明：直線OM的斜率與l的斜率的乘積為定值；(Ⅱ)略.

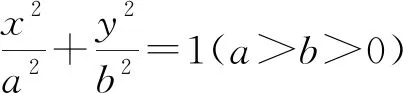
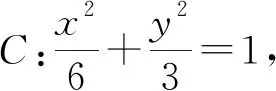
圖5

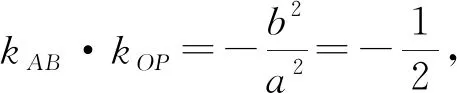
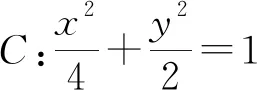
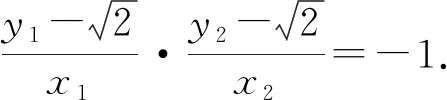
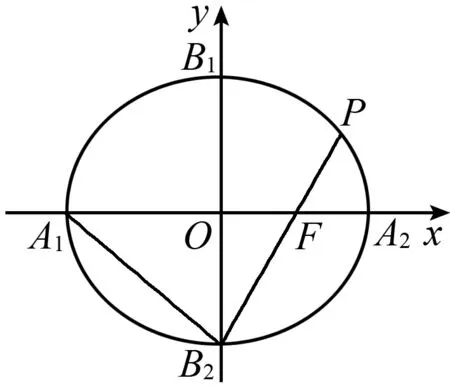
圖6

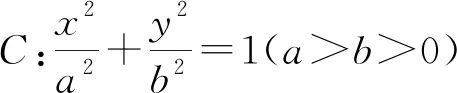
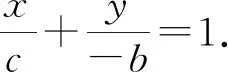
案例剖析:定點定值問題是圓錐曲線中十分重要的研究課題，蘊含著動、靜依存的辯證關(guān)系，深刻體現(xiàn)了數(shù)學的魅力，在高考中常常涉及此類問題且位于中檔題的位置.通過案例2將上述結(jié)論2的探究方法(設(shè)點法，點差法等)以及結(jié)論2都得到了運用,起到了典例示范的作用，并通過二種方法的對比訓練學生發(fā)現(xiàn)中心弦特征；挖掘弦中點的方法技巧；真正起到學以致用的作用.從具體問題入手，通過對解決方法進行總結(jié)辨析，滲透了轉(zhuǎn)化與化歸的思想,使學生能夠根據(jù)問題的條件尋找與設(shè)計更合理、更簡捷的運算途徑，并引導學生發(fā)現(xiàn)這類問題所具有的更一般性規(guī)律.

三、教學思考

美國著名數(shù)學家波利亞曾說：“一個專心的認真?zhèn)湔n的教師能夠拿出一個有意義的但又不太復雜的題目，去幫助學生挖掘問題的各個方面，使得通過這道題，就好像通過一道門戶，把學生引入一個完整的理論領(lǐng)域”.[1]在高考數(shù)學復習課教學,若沒有明確而有效的教學策略指導,學生容易缺失學習的積極主動性,復習課有可能就變得高強度低效率.紙上得來終覺淺，絕知此事要躬行,所以高三復習課要緊扣大綱,立足教材,聚焦高考,選取重點突出的問題,通過強化、類比、拓展、延伸、遷移的問題變式題組教學，促使學生成功跨越“最近發(fā)展區(qū)”，點點突破，層層推進，步步深入,培養(yǎng)學生的問題歸納、概括總結(jié)能力.而在一題多變題目演示下，學生的思維靈活性也能夠得到拓展.在解析幾何求解過程中,不斷提升學生的數(shù)學運算、邏輯推理等核心素養(yǎng)，從而使得數(shù)學核心素養(yǎng)內(nèi)化于心.讓學生體會問題的通法,進而提煉思想方法,使學生做一題會一片通一類,使學生能真正做到以不變應萬變,笑傲高考考場.