基于節點法的EIT重構技術研究

鄭皓楠

（西北工業大學，陜西 西安 710100）

0 引言

電阻阻抗成像（EIT）是基于生物體組織在不同的生理、病理狀況下的電阻抗（電導率、電阻率）分布差別較大的特點，并通過電極在生物體表面施加微小的激勵電流，從而使生物體的組織內部產生微弱的電場，利用在體表測得的電壓信號配合一定的成像算法以實現組織內部電阻抗分布圖像的重構。電阻抗成像具有用途廣泛、健康環保安全、經濟可循環使用以及快速便捷易用等優點。

1 EIT技術簡介

EIT系統的基本原理是通過多路開關向安裝在被測生物體組織表面的電極注入安全激勵信號，同時通過測量目標區域表面能夠反映阻抗信息的電壓信號，該信號經過高精度的放大電路處理后，通過相敏解調電路和A/D轉換器進行信號恢復和數字化處理，最后計算機通過圖像重構算法得到能夠反映被測區域生物體組織電阻抗變化的圖像。電阻抗數據檢測系統的功能是采集生物體組織的電阻抗及其變化信息，圖像重建根據電阻抗數據檢測系統提供的生物體組織的電阻抗及其變化信息，采用相應的重建算法對生物體組織的電阻抗及其變化信息實現圖像重建與顯示的功能[1]，如圖1所示。

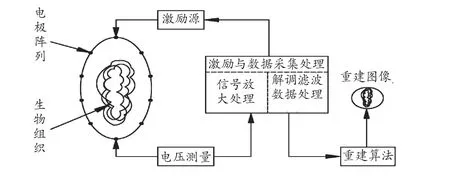
圖1 EIT成像系統

EIT成像的難點是在對其場域數學模型的合理構建上，由于生物體內的電磁場為非線性分布，因此，在實際測量中會受到接觸電阻抗的影響，而建模過程又會忽略這些因素（例如生物組織電阻抗信息虛部和生物體接觸電極后產生的電阻等），在模型構建中將高階項以有限元離散化的形式產生計算誤差，該計算誤差在迭代過程中不斷累積，導致EIT圖像重構后的分辨率較差；且用模型求解逆問題存在病態性，其病態性表現在邊界電壓出現微小變化就會造成解的巨大變化，且現有算法對區域中心的變化不敏感，對區域邊界的變化敏感[2]。此外，電阻抗成像技術計算量較大，成像速度較慢，想要提升重構圖像的分辨率就必須對物體場域進行密集剖分，該操作會導致有限元剖分呈幾何級增長。如何在提升圖像質量的同時保證不會出現計算量大幅度增加的情況，這就需要在重構算法上進行改進優化。

2 EIT正問題、逆問題求解

EIT圖像重建過程是指通過邊界測量數據進行圖像重建，對被測生物內部阻抗的分布處理主要分為正問題和逆問題2個求解過程[3]。電阻抗成像的正問題是在已知電導率分布和邊界條件的情況下求取場域內的電位分布。求解EIT正問題主要以解析法和數值計算法為主，但解析法受區域內的條件所限制，當電導率不均勻或二維形狀不規則時，其解析推導難度較大，因此首選數值法；常用的數值法包括有限元法、有限差分法以及邊界元法[4]。該文正問題計算采用的是有限元法。電阻抗成像的逆問題是在已知邊界電壓的情況下，求得目標區內電導率（電阻抗）的分布，如圖2所示。

EIT圖像重建的本質就是求解逆問題，求解逆問題的實質就是形成阻抗圖像；但是，由于逆問題的不適定性，因此，它的求解過程存在一定的難度。EIT逆問題的求解過程是1種嚴重病態非線性問題的求解過程，其主要表現在以下4個方面：1） 因為微小的邊界電壓波動就會造成解的不確定性，影響成像質量，所以對成像算法提出了很高的要求。2） 測量得到的邊界電壓數量有限，激勵信號形式單一，不足以完全反應出人體內部阻抗的變化情況。3） 場域內電導率的分布與測量邊界電壓的非線性關系，是由電磁場的軟場特性決定的。4） 電阻抗的求解是通過算法不斷迭代來獲得近似解，因此，它的值和實際值存在一定偏差。

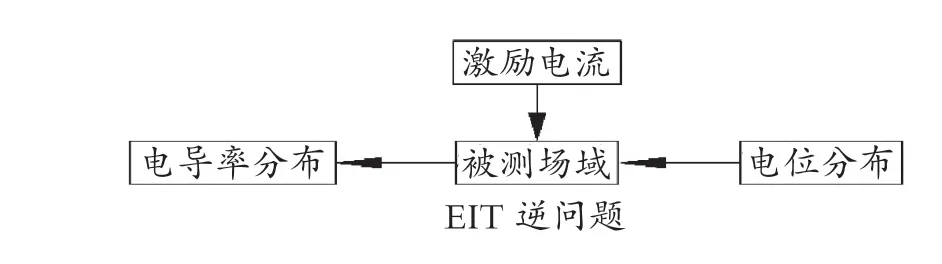
圖2 求解EIT逆問題的示意圖

為了簡化問題，假定被研究區域的電流場是準靜態場，以二維EIT問題為例，EIT的圖像重建問題實質上是求解1個低頻電流場的逆問題，即已知邊界的電流和電壓，求解內部電導率的分布。該文逆問題求解以靜態成像求解為研究對象，鑒于逆問題求解上述4種表現，因此在選擇圖像重建算法的過程中需要非常謹慎。EIT逆問題求解通常采用修正的牛頓-拉夫遜迭代算法（MNR算法）[5]。

EIT逆問題求解主要基于最小二乘理論，如公式（1）所示。

由于EIT逆問題具有嚴重的病態非線性問題，因此公式（1）常用MNR算法求解。假定將場域離散成m個單元（選用FEM三角形網格剖分方式），邊界測量電極為L個。選擇相臨電極施加激勵電流且采用相臨測量的方式，就可以獲取L×（L-3）個邊界電位數。據此可以推導出MNR算法的迭代式，如公式（2）所示。

式中：k為迭代次數。

為了解決逆問題求解的病態非線性問題，常在求解過程中進行正則化處理，EIT逆問題中最常用的正則化算法就是Tikhonov正則化算法。該算法的實質是通過構造特定形式的罰函數來實現對解的阻尼作用，以求得穩定的解。

引入正則化后，其迭代式如公式（3）所示。

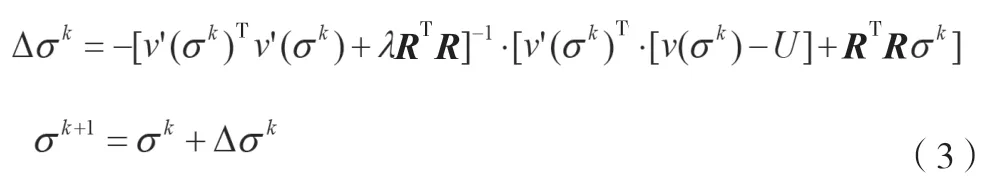
式中：k為迭代次數；λ為正則化參數；T為轉置符號；R為由FEM模型逆時針進行單元編號得到的正定矩陣；v'是電壓值關于電導率的導數。

對矩陣元素Rij，i=j時，Rij為單元數之和；i≠j時，i與j單元格相鄰，Rij=-1；i與j單元格不相鄰，Rij=0。R及正則化參數的非負性使其逆項矩陣的求解過程更加穩定。

3 基于MNR算法的中心局部細剖分模型

電阻抗成像圖像重建效果的好壞受激勵模式、數據采集精度、算法以及剖分規模等多方面因素的影響，其中剖分規模是最重要的影響因素之一。為了平衡正問題和逆問題求解過程中因疏密不同而帶來的不必要的影響，同時盡可能地避免出現計算量過大的細剖分方式，通常會采用密剖分三角形網格模型和疏剖分三角形網格模型結合的均勻剖分方式。電阻抗成像圖像重建算法中逆問題計算是建立在正問題計算之上，正問題計算精度越高，圖像重構的質量也越好；因此，正問題通常采用密剖分求解（在疏剖分單元三邊中點兩兩連接得到密剖分模型），逆問題選擇疏剖分求解。但疏密結合的均勻剖分不能從根本上解決對計算正問題和逆問題帶來的影響。因此，假定連續求解的仿真物理模型為規則的圓域（圓域半徑為16），運用有限元剖分軟件[6]選擇有限元法（FEM）進行三角形剖分，對以中心區域為圓心，半徑為1/2的圓形區域進行中心區域局部細剖分（如圖3所示），應用牛頓-拉夫遜算法進行圖像重構，并將中心區域的目標與粗細剖分界面的目標進行對比，如圖4所示。

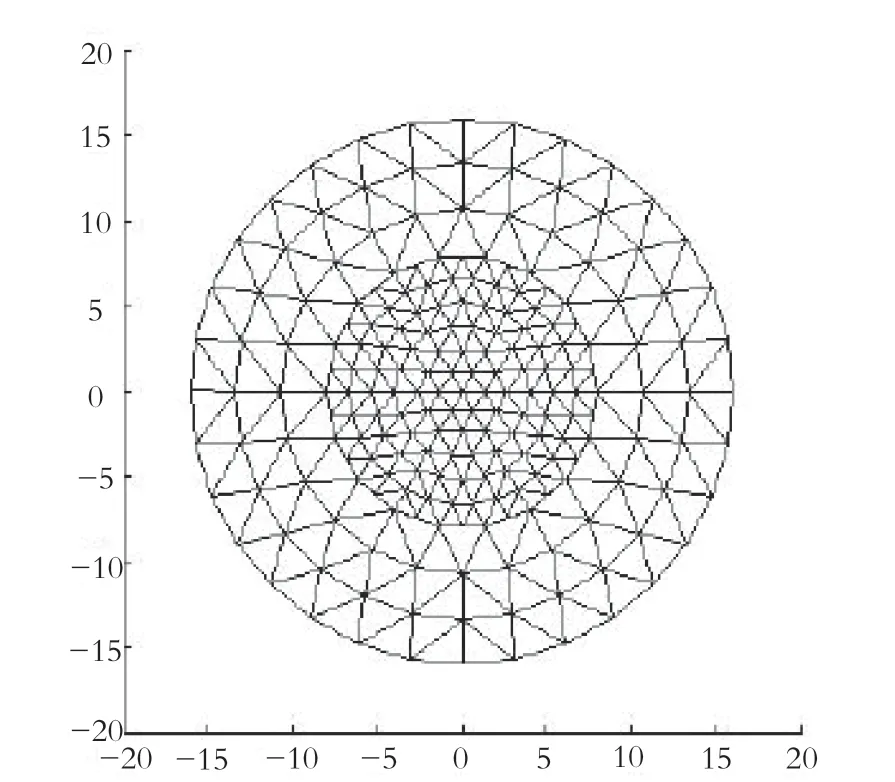
圖3 中心區域局部細剖分模型

圖4（a）和圖4（b）分別是異物位于中心區域的疏、密剖分和中心區域密剖分的仿真成像，圖4（c）和圖4（d）分別是異物位于非中心區域的疏、密剖分和中心區域密剖分分界面處的仿真成像。對比圖4（a）和圖4（b）可知，圖4（b）成像均勻，偽影小，定位準；對比圖4（c）和圖4（d）可知，疏、密剖分和中心密剖分仿真成像相差不大。通過以上仿真成像對比發現，如果異物處在分界面上，那么中心局部密剖分相對疏、密剖分仿真得到成像結果改善不大；如果異物整體處于密剖分部分內，那么中心局部密剖分相對疏、密剖分就可以得到更加良好的仿真效果。因此，對于異物采用中心局部細剖分有助于提高重構成像的質量。綜上所述，細剖分不一定要處于中心位置，它可以根據異物的位置靈活地確定細剖分剖分的位置。

4 基于節點法的EIT圖像重構技術及仿真實驗

4.1 重構算法

采用基于牛頓-拉夫遜算法的局部細剖分能夠在無噪仿真實驗中構建高質量的EIT阻抗變化分布圖，但電阻抗成像圖像重建效果的好壞受多方面因素的影響，其中包括測量噪聲。為了使仿真實驗成像切合實際，需要對其進行加噪處理。仿真實驗表明，經過加噪處理后的數據重建的異物區域圖像會產生向粗細剖交界面偏移的現象，這會導致EIT重構圖像存在偏差，形成該現象的原因多為FEM網格單元剖分不均勻；而將單元退化成節點后進行成像，由于節點的位置同等，因此會最大程度地避免出現剖分不均勻的問題，從而有效地解決了異物區域發生偏移，產生定位偏差的現象。其過程如下：1） 設定迭代條件，為無窮小，U為實測邊界電壓值，Uk為均勻阻抗時正問題求解的邊界電壓值，滿足時，可以終止迭代并進行圖像重構，不滿足該條件則進行下一步。2） 基于單元阻抗信息計算單元雅克比矩陣J（σk）。3） 根據第2步的結果計算節點雅克比矩陣及節點阻抗迭代步長h，h的計算公式如公式（4）所示。

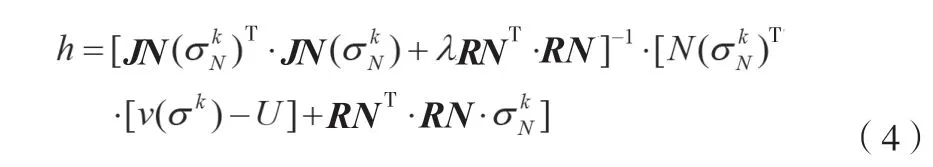
圖4 單目標仿真圖像

4.2 仿真成像

以單目標為仿真對象，向仿真數據中加入10 db、40 db的高斯白噪聲，通過節點法形成EIT圖像重構，如圖5所示。

圖5（a）和圖5（b）為10 db信噪比條件下局部細剖分及基于節點法的局部細剖分成像結果，圖5（c）和圖5（d）為40 db信噪比條件下局部細剖分及基于節點法的局部細剖分成像結果，對比可知在信噪比同為40 db（較高）的條件下，2種成像質量雖有差別（圖5（d）優于圖5（c）），但其差異較小；在信噪比同為10 db的條件下，2種成像質量差別很大，圖5（b）的效果比圖5（a）的效果要好。由此可見，信噪比越小，節點法的成像效果越好。綜上所述，使用節點法成像能夠去除因局部細剖分而產生的影響圖像重構質量的不利因素，因此，對異物采用局部細剖進行圖像重建是可行的。

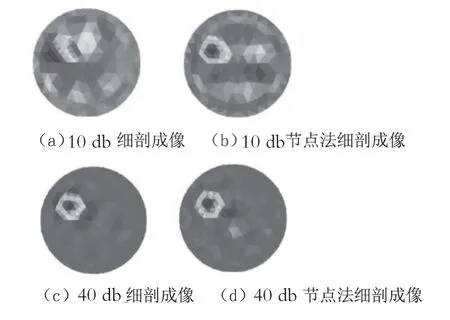
圖5 不同噪聲條件下單目標仿真成像

5 EIT應用討論

電阻抗成像技術是近幾十年發展起來的新一代無損功能成像技術，其與現有成像技術相比具有很多優點，但是仍然存在很多需要研究解決的問題。該文利用現有技術所提供的結構先驗信息構建了可以有效提升模型準確性的EIT仿真模型，通過MATLAB平臺[7]進行仿真計算，在牛頓-拉夫遜算法的基礎上改進網格剖分，構建基于異物區域的局部細剖分模型，在仿真過程中展現了一定的優越性，但是在抗噪性能上還存在一定的改進空間；因此，將單元細化成節點，通過節點進行成像，可以減少邊界偽影，提高成像質量，得到高分辨率的圖像。

6 結語

電阻抗圖像重建在臨床研究中仍然具有一定的挑戰性，如果在臨床研究中與其他醫學圖像結合研究將會進一步推動它的應用和發展，還可以最大程度地發揮其無損功能性成像的優勢。改進后的EIT圖像重構算法抗噪性能還有待提高，且未對生物體組織進行試驗，因此后續還應該進一步提高算法成像的精度，加深對于逆問題的求解。總之，構建具有較高檢測靈敏度和性噪比、有足夠的空間分辨率和阻抗分辨率[8]以及優化現有算法重建高質量圖像效果的成像系統是當前科研工作者努力的方向。