對定量分析數學化的若干思考

甘峰，褚泳欣，楊維嵐

中山大學化學學院，廣州 510275

有人將分析化學尊為“化學之母”，以彰顯其在化學學科的建立和發展過程起到的至關重要的作用。然而也有人將其視為“化學的婢女”，以強調其在化學學科的建立過程中只起到輔助性的作用。不同的人基于自己不同的“利益”取向，由此對分析化學表現出不同的態度，這本來是可以理解的。但是，由于不同的人所處的科學地位的不同，他們的行為卻在一定程度上延緩了分析化學的發展，甚至在破壞分析化學的發展。例如，國外的很多高校在20世紀取消了分析化學學科，取而代之的是將分析化學分拆到其他化學學科之中。中國也曾經出現過類似的思潮，幸未最終發生。如何糾正曾經發生在分析化學上的錯誤認識，以及防止類似的事情再度發生，是擺在每一位分析化學家面前的一個重要問題。而重中之重，則是要找到問題的根源之所在。

分析化學處于一個較為尷尬的地位有其歷史淵源。其實不只是分析化學，整個化學學科均處于一個尷尬地位，究其歷史可追溯到康德[1]。康德認為“...chemistry can’t be anything more than a systematic art or experimental doctrine, never a science proper, because the principles of chemistry are merely empirical and can’t be presented a priori in intuition...”在康德看來，化學由于過于經驗化使其不能成為“理性的科學”。在現代的科學家中，認為化學不能成為獨立學科的人也不少，有些科學家則更為極端。例如狄拉克[2]認為“The underlying laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that exact applications of these laws lead to equations which are too complicated to be soluble.”

現代科學的一個顯著特點是數學化，這是邁向(康德所指的)理性的科學的必然途徑。物理學家一直致力于物理學的數學化并且取得了巨大的成功。物理學的某些成果，如量子糾纏、引力波等概念，均是在物理理論數學化形式下從理論上首先得到并最終為實驗所證實。化學如果視自己為科學共同體中的一分子，理應(也必將)遵循科學共同體的發展趨勢，實現化學的數學化。由于化學分為無機化學、有機化學、物理化學和分析化學四個領域，化學的數學化意味著這四個領域均實現數學化，難度非常之大。2017年，俞汝勤院士[3]在中國海南海口市舉行的International Congress on Analytical Sciences會議上，提出借助化學計量學實現分析化學數學化的思想，這是對整個分析化學具有非常重要影響的歷史事件。

本文的目的是對分析化學的一個重要分支——定量分析化學的數學化現狀進行分析和討論。定量分析在整個分析化學中起到前承定性分析后啟結構分析的作用，其數學化進程對整個分析化學的數學化起到至關重要的作用。由于定量分析事實上被劃分為化學定量分析(主要是容量分析法)和儀器定量分析，我們將對二者進行分別的分析和討論。我們期望能夠回答若干問題，例如定量分析化學是否已經實現了數學化？如果沒有，那么又該如何實現其數學化？化學計量學能否幫助定量分析實現數學化？作者認為定量分析的數學化問題，不僅僅是分析化學自身理論發展的需要，也是實現分析化學整體的數學化，乃至化學整體的數學化的必經之路，具有非常重要的科學意義。

1 化學定量分析的數學化現狀

化學定量分析法主要是指經典分析化學中的容量分析法，它依據溶液中的化學反應為基礎進行定量分析。在化學定量分析中，化學反應組分之間的化學計量關系起到決定性的作用。待測物必須直接或者間接地與某個標準試劑(通常稱為滴定劑)以固定的化學反應計量關系進行反應，其含量才能通過消耗的標準試劑的量進行計算。無論涉及的反應的數目和復雜程度如何，由于化學反應中組分之間固有的化學計量關系不變，因而多數情況下可以建立待測組分含量與標準試劑用量之間準確的數學方程，從而計算出待測組分的含量。正因為如此，化學定量分析法也被稱為是絕對定量分析方法[4]。以NaOH滴定HCl這個最簡單的定量分析為例，化學反應式如下：

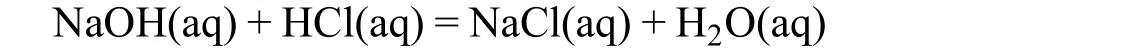
由于反應的計量關系為1 : 1，所以達到計量點時可以用下式表述：

這里，c(HCl)和c(NaOH)分別為HCl和NaOH的初始濃度；V0是HCl的初始體積，Vsp是計量點時加入的NaOH的體積。

式(1)即等同于物理學中的杠桿平衡，而加入的NaOH的摩爾數即等同于砝碼質量。然而，式(1)自身并沒有提供直接的方法來指示何時達到計量點(即杠桿的平衡點)。通常情況下，容量分析法在反應體系內加入化學指示劑，利用其變色來指示滴定終點，以此對計量點進行估計。由于對指示劑的變色的判定因人而異，這讓化學定量分析法看上去更像一門技藝而非科學。更為糟糕的是，指示劑本身實際上也會參與到定量反應過程中去，并改變了化學計量點的位置[5]。打個通俗的比喻，指示劑實際上扮演了“運動員”和“裁判員”的雙重身份，因而它很難做到客觀地指示化學計量點。

化學定量分析中的通常做法是以指示劑的影響小從而使得最終產生的誤差可忽略為理由將指示劑的影響不計入到方程(1)的理論框架中。但這種人為地將本來就包含的因素強行剝離出去的做法也使得化學定量分析的理論框架不完善。當前，雖然可以建立嚴格的數學方程去描述滴定過程[6,7]，但是，這些方程本身并沒有很好地解決計量點的指示問題。并且，這些滴定方程更多地用于描述滴定過程，而不是直接用于定量分析。

國外一些分析化學教科書[8]介紹了采用對滴定曲線求導的方式對化學計量點進行估計，但未給出嚴格的數學證明。在實際的定量分析中，這種做法也很少見有實施。更多見到的是基于儀器測量采用Gran圖法[9]對化學計量點進行估計，一些自動滴定儀也采用了這種方法。采用Gran圖的方法因不會顯著地介入到反應過程中，被認為是優于采用指示劑的方法。然而，Gran圖法的數學模型并不準確。仍以NaOH滴定HCl的反應為例，Gran是從下式開始進行數學推導過程(即參考文獻[9]中的方程(1))：

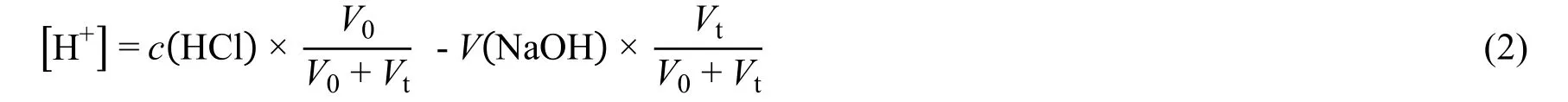
這里，[H+]是加入Vt體積的NaOH后體系的氫離子濃度。

如果在化學計量點的位置加入的NaOH體積為Vsp(Vt= Vsp)，由于有c(HCl) × V0= c(NaOH) ×Vsp，所以從式(2)得到[H+] = 0。然而，化學事實表明上述的反應在化學計量點時體系的氫離子的濃度實際上為[H+] = 1.00 × 10?7mol·L?1。這表明，Gran 圖法的理論誤差會達到(0 - 1.00 × 10?7)/1.00 ×10?7= ?100%。顯然，Gran圖的數學模型并不能令人滿意。

所以，不能認為已經建立了化學定量分析完備的、自洽的數學理論體系。由于化學定量分析有逐步被儀器定量分析取代的趨勢，目前很少人將其作為重要的研究領域去深入探索，相關的數學理論方面的研究未見有重大的進展。有趣的是，依附于滴定分析構建起來的滴定曲線方法，卻越來越多地在物理和化學參數的測量方面發揮著作用。限于篇幅，這里不做進一步討論。

2 儀器定量分析的數學化現狀

儀器分析法的引入對分析化學產生了巨大的促進作用，也帶來了負面的影響。由于儀器分析法所采用的測量原理通常源自物理學，因而也被稱為是物理分析法。更為極端的情況是，正因為儀器分析法的這個特性，導致20世紀60年代左右在美國的一些著名的大學中取消了分析化學的職位，理由居然是“它只是應用物理化學而已”。

如果把視線轉到定量分析領域，由于儀器定量分析法采用了物理學原理并輔之以一定的數學形式，似乎從一開始就實現了數學化。以原子吸收法為例，Walsh[10]于1955年提出了利用原子吸收效應來進行定量分析的理論基礎，其數學方程如下：

這里，Kmax是吸收系數的峰值；λ是波長；D是多普勒變寬；e是電子的電荷；m是電子的質量；c是光速；N是原子的數目；f是振子強度。

式(3)表明原子吸收系數峰值與原子數目成正比，也就是與組分濃度成正比。由于該方程中其他相關的量在一定條件下是常數，而 f可以通過標準樣品得到，Walsh由此推測原子吸收法有可能成為絕對定量分析方法(文獻中用詞absolute analysis)，即只需要通過測量值Kmax直接計算出N。

然而，實際的情況是式(3)并沒有被直接用于絕對定量分析。具體原因非常多，此不贅述。迄今為止，儀器定量分析法基本上均采用一種稱為校正的技術，即用待測物的標準品配制一系列標準溶液并測量其信號強度，由此建立濃度與測量信號強度的線性方程，其一般形式如下：

這里，y是測量信號強度；k是回歸系數；c是組分濃度；η是與儀器狀態及分析條件相關的量；ε是與隨機誤差相關的量。未知樣品在同一儀器和同樣分析條件下測量其信號強度之后，可以通過式(4)計算出其濃度。

然而，如果對儀器定量分析進行仔細的思索就會發現，它確實不再基于化學反應理論。雖然化學反應在樣品處理和生成產物等階段依然發揮著作用，但是化學反應的計量平衡關系不再用于定量分析。所以，將儀器定量分析劃分為物理分析并不為過，畢竟關鍵的理論還是物理學原理。這也就不難理解Liebhafsky會感慨地說“Like it or not, the chemistry is going out of analytical chemistry”[11]。

儀器定量分析的關鍵在于應用式(4)，它本身是一個純粹的數學方程，不包含任何的物理或化學體系的參數，將其視為物理分析和化學分析的基礎理論顯然均不能成立。并且，測量得到的信號強度是相對量而不是絕對量，不能從測量信號強度本身直接計算出物質的摩爾數，所以用式(4)作為儀器定量分析的數學基礎本身也不完備。綜上所述，我們尚不能認為儀器定量分析的數學化已經完成。

從儀器定量分析的發展動態來看，從早期的利用式(4)建立一元線性回歸方程，已經過渡到了基于化學計量學的多元校正理論實現多元線性回歸、主成分回歸、偏最小二乘回歸等。而所涉及的儀器，也從早期的紫外-可見光譜儀等，發展到近紅外光譜儀、拉曼光譜儀等[12-16]。但是，所有這些應用都可視為是式(4)的擴展，不能從本質上改變儀器定量分析沒有實現數學化的現狀。

3 化學計量學對定量分析數學化的作用

化學計量學[17-19]被引入到分析化學之后對分析化學的諸多領域產生了深遠的影響，尤其是在定量分析領域。例如，近紅外光譜技術和拉曼技術與化學計量學相結合之后，構建出新的定量分析方法[20,21]，極大地改變了傳統的定量分析方式。而張量類型的數據的構建和多維分辨算法的引進和建立[22,23]，也將以完全不同的方式改造現有的定量分析方法。原因在于，基于張量數據的多維分辨方法從理論上可以得到唯一解[23]，這意味著基于張量數據在理論上是可以得到化學體系真實的光譜信息和濃度信息，這將使得定量分析基于體系真實信息的基礎上而不是抽象因子的基礎上。

然而，如果細致分析會發現，采用這條途徑依然無法達到理想的目標。例如，如果基于二維熒光技術得到的張量信號可以用三線性模型描述[22]，即：

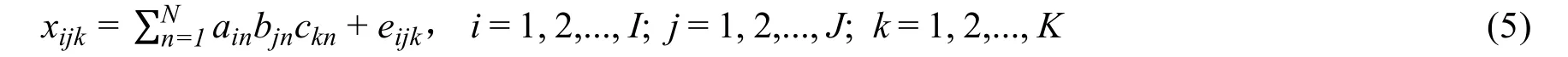
這里，xijk是三維陣列的第ijk個元素；N是有信號響應的組分數；ain是矩陣AIN的第in個元素；bjn是矩陣BJN的第jn個元素；ckn是矩陣CKN的第kn個元素；eijk是殘差三維陣列的第ijk個元素。這里的矩陣CKN又稱為濃度矩陣，其每一列是一個組分的濃度向量。

在不存在光譜相似性和濃度共線性的情況下，從模型(5)中可以得到唯一解，從化學的角度可以認為是得到體系中組分的真實光譜以及真實濃度。吳海龍等[24]的研究工作也表明，確實可以從該模型中分解得到目標組分的熒光光譜，且與對應組分的實際熒光光譜形狀相同。這是否意味著同時得到的濃度向量就是體系中組分的真實濃度變化呢？真實的情況并非如此。分解得到的濃度向量中的元素并非是真實的濃度值，而只是與真實濃度成比例的值，還必須采用校正的方法才能真正得到體系組分的真實濃度值。這樣一來，基于化學計量學的張量理論得到的“真實”信息，最終也不能實現絕對定量分析，而必須重新回到校正的老路上去。所以，化學計量學尚未推動定量分析實現數學化。

4 結語

總體而言，定量分析的數學化當前還處在概念階段，當前尚無定論。從上面的討論中可以看到，定量分析在應用數學理論方面有了巨大的發展，這使得它初步形成了理性的科學的形態。如何實現定量分析的數學化仍是需要探討的問題。但是應該認識到在定量分析中簡單地引入(或者改造)現有的數學理論不能視為是定量分析化學數學化的正確道路。從上面的分析中也可以看到這條路未必能夠走通。化學定量分析的數學化似乎應該在基于化學反應理論的基礎上去構建具有化學反應內稟變量的數學理論，這個理論還必須是完備的、自洽的，并且能夠在某些條件下升華為定理或歸結為定律。如果定量分析數學定理能夠構建成功，則對于定量分析的數學化顯然具有最大的支持效果。從這一點上看，容量分析法在將化學反應和數學相結合構建數學理論體系方面實際上是有成效的，放棄容量分析理論而僅依靠儀器定量分析去尋找定量分析的數學化未必是正確的道路。這也提示我們，當前的分析化學教學中，對于容量分析理論的教學不但不應該減少，反而更應該加強。而對于其內容體系也應該做更為深入的拓展。例如，當前的大多數分析化學教材中的容量分析部分，宜將有關酸堿滴定通式和配位滴定通式的內容加入。與此同時，對于滴定體系的內容，宜從以往的只關注待測物的濃度變化，過渡到對滴定體系中所有組分的濃度進行準確的數學描述。我們預期，如果定量分析的數學得以實現，則定量分析有可能進入一個新的境界。