基于稀疏貝葉斯學習的空間緊鄰信號DOA估計算法

王琦森 余 華 李 杰 董 超 季 飛 陳焱琨

①(華南理工大學土木與交通學院 廣州 510640)

②(自然資源部海洋環境探測技術與應用重點實驗室 廣州 510300)

③(華南理工大學電子與信息學院 廣州 510640)

④(國家海洋局南海調查技術中心 廣州 510300)

1 引言

波達方向(Direction-Of-Arrival, DOA)估計，廣泛應用于聲吶、雷達和無線通信等許多領域[1]。經過幾十年的發展，出現了有超分辨能力的子空間類方法， 如MUSIC[2]等。然而在低信噪比等環境中，這類算法的性能會明顯降低。

近年來的稀疏重構類算法克服了子空間類方法的缺點。 ?p范數法是經典的稀疏類方法之一，其代表是?1范 數。文獻[3]首次把DOA估計轉化為?1范數問題，提出了奇異值分解的L1范數重構算法(L1 reconstruction-Singular Value Decomposition, L1-SVD)，并利用網格細分法來提升精度。然而 ?p范數類算法對信號的重構并不準確[4]，其正則化因子難以確定，網格細分策略會使得基之間的相關性增強而導致性能的降低[3]。

稀疏貝葉斯學習(Sparse Bayesian Learning,SBL)算法最初作為機器學習在文獻[5]中提出，隨后被引入稀疏信號處理領域[4,6]，表明了SBL相對于?p范數法具有更好的重構性能。文獻[7]把SBL用于DOA估計，提出了相關向量機方法(Relevance Vector Machine, RVM)，該方法利用期望最大化(Expectation Maximization, EM)對信號后驗概率密度函數進行最大化來完成信號空間功率的估計，并提出了一種后處理高精度算法來實現離格(offgrid)DOA估計，相比網格細分方法提高了計算效率和精度。文獻[8]用泰勒展開把離格DOA誤差引入陣列流形矩陣，提出離格稀疏貝葉斯推斷 (Off-Grid Sparse Bayesian Inference, OGSBI)，能在稀疏的網格下實現較準確的估計；文獻[9,10]使用了一種線性插值方法進行離格DOA建模，其效果和文獻[8]類似；文獻[11]基于文獻[8]的泰勒展開模型提出了網格自適應方法，使用分布式傳感器對室內近場信號進行2維定位；文獻[12,13]提出求根稀疏貝葉斯(root-Sparse Bayesian Learning, root-SBL)，即基于SBL理論使用多項式求根法在每次迭代里解得離格誤差，相比文獻[8]提高了計算效率和對網格間距的穩健性。文獻[14]把SBL應用于海洋匹配場處理進行聲學探測。近年來，SBL還廣泛應用于MIMO信道估計[15]、互質陣列[16]和寬帶測向[17]。其中文獻[16]使用變分貝葉斯(Variational Bayesian Inference, VBI)，針對協方差向量使用泰勒展開模型進行離格DOA估計。

但是，對于空間緊鄰信號的DOA，密集的網格點提高了算法的估計精度卻增加計算負擔，而稀疏的網格點減小了計算負擔的同時以犧牲估計性能為代價。針對此問題，本文提出一種基于稀疏貝葉斯學習的空間緊鄰DOA估計算法，包括3個步驟：(1)超參數的預估計；(2)網格插值優化和超參數的二次估計；(3)改進的離格DOA估計。第(1)步通過最大化陣列輸出的邊緣似然函數，推導了信號在拉普拉斯先驗分布下的不動點迭代公式，相比其他SBL算法有著更快的收斂速度，并通過計算信號協方差矩陣的對角線元素而比其他SBL算法具有更低的計算復雜度；第(2)步使用最大似然方法2次估計噪聲方差，并根據譜峰特征對網格點進行插值優化，在新網格點集的基礎上2次估計信號功率；第(3)步推導了信號在拉普拉斯先驗分布下的邊緣似然函數關于角度的最大化公式以進行離格DOA搜索。仿真表明本文所提算法比其他經典SBL算法具有以下優勢：(1)對空間緊鄰信號的DOA具有更高的估計精度和分辨率；(2)低信噪比下的估計性能和計算效率更好；(3)可以使用大迭代門限取得更高的估計精度。

2 信號模型及稀疏表示

假設有 K 個遠場窄帶信號同時入射到具有 M個陣元的均勻線陣，定義方位角θ =[θ1,θ2,··· ,θK]為信號入射直線與陣列法線的夾角，則陣列在 t時刻的輸出數據為

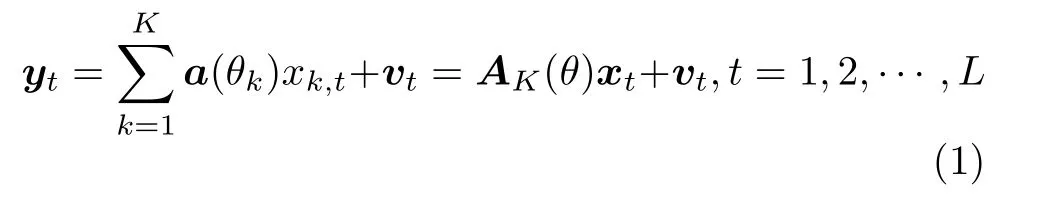
其 中， yt=[y1,t,y2,t,···,yM,t]T是 陣 列 接 收 數 據；xt=[x1,t,x2,t,···,xK,t]T是 K 個 信 號 在t 時 刻 的 波形； AK(θ)=[a(θ1),a(θ2),···,a(θK)] 是 K個信號的陣 列 流 形 矩 陣；a(θk)=[ej2πfτk,1,ej2πfτk,2,···,ej2πfτk,M]T是第k 個信號對應的陣列流形向量，其中f 是信號頻率，τk,m=Dmsin θk/c 是第k 個信號在第m個陣元到參考陣元間的時延，c 是信號傳播速度， Dm是 第m 個陣元到參考陣元的距離；vt是高斯白噪聲向量，其方差為σ2。考慮把整個空域角度范圍均勻劃分成 N個網格點，每個網格點代表一個可 能 的 入 射 方 向，即 Θ =[?1,?2,···,?N]，并 有K <

其中，過完備陣列流形矩陣A(Θ)=[a(?1),a(?2),···,a(?N)]∈CM×N可以簡化為 A ，是稀疏向量，里大多數元素為0、只有少數元素不為0，中非0元素的位置代表信號的估計DOA，如果有 L個快拍，式(2)的單快拍模型就變為多快拍模型，即可以延伸為[3]

3 稀疏貝葉斯概率分布模型

稀疏貝葉斯學習首先要建立促進稀疏的先驗分布[4,5]。假設信號的各個元素相互獨立，各列服從均值為0、方差為 γ =[γ1,γ2,···,γN]T的復高斯分布，則幅度的概率密度函數為

由貝葉斯原理可得源信號關于陣列接收數據的后驗概率為

4 改進算法

為了提高DOA估計的精度并降低計算復雜度，本文提出一種基于稀疏貝葉斯學習的DOA估計改進算法，主要包括3個步驟。首先是超參數的預估計，此部分利用不動點迭代算法的快速收斂特性預估信號的空間功率譜，并通過估計信號協方差矩陣的對角線元素而避免了估計整個協方差矩陣來降低計算復雜度；其次，根據上一步功率譜的譜峰特征進行網格點的插值優化，并對噪聲方差和信號功率進行2次估計，從而提高對空間緊鄰DOA的分辨能力；最后通過推導似然函數關于角度的最大化表達式來進行離格DOA搜索，進一步提升估計精度。

4.1 超參數的預估計

4.2 網格插值優化及超參數2次估計

由于譜峰之間保留的網格點可能有重疊，所以Θnew網格點數的最大值為7 K。與文獻[3]中提出的網格細分方法不同，本文方法進一步利用了SBL算法的功率譜峰包含兩較大幅值的譜峰特征，且沒有對網格進行多級細分。如圖1所示，粗短線代表原始網格點，豎直點劃線是第 k個信號的實際DOA，豎線代表能量幅值，三角形為插入的網格點，使用這樣的網格點插值優化方法的好處在于：增強了2次估計后的空間譜對空間緊鄰信號DOA的分辨率，同時提高了計算效率。

圖1 網格點插值優化

隨后進行噪聲方差的2次估計，這是因為準確的噪聲方差可以提供更好的稀疏重構效果[7]。由文獻[7,18]可以得到最大似然方法的噪聲方差估計

4.3 改進的離格DOA估計

2次估計后仍然存在DOA和網格點的失配誤差，這里參考文獻[7]的高精度DOA估計。相比文獻[7]的方法，改進之處是推導了拉普拉斯先驗分布下的邊緣似然函數關于角度的最大化表達式，保證性能的同時降低了計算量。

4.4 算法流程和運算復雜度分析

本文所提算法簡稱為網格插值-多快拍稀疏貝葉斯學習 (Grid Interpolation-Multiple snapshot Sparse Bayesian Learning, GI-MSBL)，流程總結如下：

步驟 1 信號功率的預估計。

5 仿真分析

表1 算法的計算復雜度

5.1 空間功率譜圖對比

兩個獨立等功率的隨機信號DOA為–3.05°和1.57°，信噪比均取10 dB，進行150次隨機試驗，得到空間譜如圖2 所示。圖2 的點劃線為真實DOA，實線為空間譜，為了清晰展示取–20°～20°的方位角范圍。對GI-MSBL算法，結合式(21)，在插入網格點集 ΘIT后 ，總的網格點集Θtotal等 于 原 始 網 格 點 集 Θ 與ΘIT取 并 集：Θtotal=Θ ∪ΘIT，記Θtotal包含的網格點數為Ntotal，注意Θnew是Θtotal的一個子集，把Θnew里網格點對應的信號空間功率值賦值給Θtotal里對應網格點處的功率，再把網格點集 Θtotal里除網格點集Θnew以外的信號功率置0，作圖時，橫坐標為 Ntotal個網格點Θtotal對應的方位角，縱坐標是歸一化信號功率幅值，從而得到圖2(a)的空間譜。從圖2可以看出GIMSBL比iRVM-DOA的譜峰波動更小，這是因為網格優化插值方法以及超參數的2次估計增強了對緊鄰DOA的分辨率。這里只選取iRVM-DOA進行對比 ，其余算法與之類似，受篇幅所限不在此一一列出。

圖2 算法的空間譜對比

5.2 不同信噪比下的估計精度和運算效率比較

兩個獨立等功率的隨機信號角度為(? 3+u)°和(3 +u )°，u 從角度范圍[-GRI,GRI]內隨機選取(避免固定角度的影響)，信噪比從–6～20 dB變化，每個信噪比下做150次隨機試驗，結果見圖3(a)。低信噪比下，GI-MSBL0和GI-MSBL的誤差都小于其他算法，這是因為超參數的2次估計增強了低信噪比的稀疏恢復能力。GI-MSBL算法在高信噪比下精度更高，這是網格插值方法帶來的性能提升。由于所提不動點迭代公式(17)具有很快的收斂速度，且不同于其他SBL算法估計整個信號協方差矩陣，所提算法只估計信號協方差矩陣的對角線元素，所以圖3(b)的GI-MSBL方法有著優于其他SBL類方法的運算效率。

5.3 不同DOA間隔下的分辨能力比較

固定信噪比5 dB，兩個獨立信號的DOA分別為( ?3+u )°和(3 +?θ+u) °，DOA間隔? θ從3°到11°變化，每個? θ下做150次隨機試驗，見圖4。圖4(a)中，在間隔3.5°到5.5°的范圍內，GI-MSBL誤差最小 。圖4(b)中GI-MSBL在? θ＜4.5°時分辨概率最高。

5.4 不同迭代門限下的估計精度和計算復雜度比較

信噪比固定為5 dB，迭代門限ε 從0.001到0.1變化，其余條件同5.2節，每個 ε下做150次隨機試驗，見圖5。圖5(a)中，所提算法在迭代門限較大時估計誤差最小。圖5(b)中根據表1的平均復數乘法次數來衡量計算復雜度，GI-MSBL0以及GI-MSB L平均復數乘法次數最少。

6 結束語

為了改進對空間緊鄰信號DOA估計的精度和計算復雜度，本文提出一種基于網格插值的多快拍稀疏貝葉斯學習 (GI-MSBL) 算法，改進算法比其他經典的稀疏貝葉斯學習算法具有以下優勢：(1)對空間緊鄰DOA具有更好的估計效果；(2)低信噪比下估計性能更好，計算效率更高；(3)能使用大迭代門限取得更高的估計精度。另外，對于水下寬帶信號，通過傅里葉變換在頻域對每個頻段即可以使用所提算法。

圖3 不同信噪比下的估計性能和運算效率

圖4 不同DOA間隔下的分辨能力比較

圖5 不同迭代門限下的估計精度和計算復雜度