穩健型雙層疊組LASSO逆合成孔徑雷達高分辨成像算法

黃 博 周 劼 江 舸

(中國工程物理研究院電子工程研究所 綿陽 621999)

1 引言

逆合成孔徑雷達(Inverse Synthetic Aperture Radar, ISAR)是一種全天時、全天候的主動微波監視手段，能夠對非合作目標進行高分辨成像，已廣泛應用于精確制導、目標檢測等軍事和民用領域[1]。ISAR高分辨成像中距離向分辨率主要依靠發射大帶寬大時寬信號而形成，方位向分辨率則取決于觀測期間非合作目標本身相對雷達視線角度變化的大小，不過由于非合作目標通常會有較為復雜的運動軌跡，這將對ISAR成像分辨率產生一定影響，雖然可以通過減少成像積累時間來降低復雜運動的影響，但這一操作同時也會降低方位向分辨力[2]。針對這一問題，文獻[3,4]基于稀疏信號假設，結合壓縮感知(Compressed Sensing, CS)理論[5]對ISAR方位向信號進行頻率分析，有效地解決了短孔徑下成像分辨率下降問題。常見的壓縮感知稀疏恢復類算法有貪婪類算法，如經典的正交匹配追蹤(Orthogonal Matching Pursuit, OMP)算法[6]，但由于稀疏度的約束，該算法解的稀疏度不高，重建精度有限。另外常見的還有貝葉斯壓縮感知類算法[7]，此類算法的優點是成像精度高，但最大的缺點是計算復雜度高，運算速度慢。針對上述問題，Boyd等人[8]于2011年重新綜述并提出適用于大規模分布式計算系統和優化問題的交替方向多乘子方法(Alternating Direction Method of Multipliers,ADMM)。ADMM方法同時結合了對偶上升法(dual ascent)的可分解性，形成了將全局問題分解為局部子問題后交替優化求解的框架。傳統基于?1范數正則化線性回歸(LASSO)的ADMM稀疏特征增強算法能適應ISAR回波信號高維特征和大規模數據這一特點，在應用于SAR稀疏特征增強成像時實現收斂速度快和恢復精度高的有效結合，并具有良好的穩健性與有效性[9]，是雷達成像中較為廣泛應用的凸優化類方法。

然而，基于?1范數正則化LASSO模型的ADMM算法仍然有一定的局限性。在實際ISAR成像中，成像目標一般具有一定的聚類性先驗特征信息，目標散射點空間分布存在一定的聚集特性，而基于LASSO模型的ADMM方法稀疏成像時未考慮此類先驗信息，從而很容易在稀疏恢復的同時丟失散射體本身的結構特征，降低了成像結果目標的連續性結構特征提取精度。因此若能充分利用這些聚類先驗信息，ISAR成像精度勢必將得到有效的提升。Yuan等人[10]于2006年提出經典的結構組LASSO模型，該模型將LASSO模型的單變量稀疏性推廣到了結構組變量稀疏性，通過將所有變量分組，并在目標函數中對每組變量施加 ?F范數懲罰，使得整組系數同時為零，從而達到組水平的稀疏特征。然而Yuan等人提出的組LASSO模型是基于簡單的變量隨機分組方式的變量選擇，并且各變量之間不可重疊，即很容易出現組中有用信息隨無用信息一同被剔除的情況。

因此，本文提出一種有效應用于ISAR回波復信號重建，基于穩健型雙層疊組LASSO回歸模型的交替方向多乘子算法(Robust and Two-tier Group LASSO-Alternating Direction Method of Multipliers, RTGL-ADMM)，該算法在方位向和距離向分別分組并層疊后，求得?1/?F混合范數的閉合解，從而同時實現組間稀疏和組內平滑處理，可以有效提升傳統ISAR成像的精度。本文首先建立矩陣形式信號模型，然后采用所提RTGL-ADMM算法對該回波信號模型進行求解。RTGL-ADMM算法先對包含有保真項和增廣拉格朗日項的嶺回歸問題求得其閉合解，然后根據?F范數正則項和拉格朗日項推導?F范數對應的鄰近算子。最后，在RTGLADMM框架中利用高斯-賽德爾(Gaussian-Seidel)思想更新對偶變量。本文在實驗部分采用ISAR模式下的仿真數據與Yak-42實測數據，將所提算法與基于LASSO的ADMM算法進行定性對比實驗，繼而利用相變曲線圖定量分析RTGL-ADMM在不同參數調節下的成像能力，從而有效驗證了本文所提RTGL-ADMM算法應用于ISAR高分辨成像時的可行 性、穩健性與優越性。

2 ISAR回波信號模型

圖1(a)所示為ISAR成像幾何模型，為了便于分析，ISAR成像中將旋轉目標相對于雷達的運動分解為平動分量與轉動分量，目標運動軌跡為CB，由于目標A點與B點存在平動分量，因此可等效目標軌跡為C-A，此時C點與A點間存在影響ISAR成像分辨率的轉動分量，但在產生平動分量時，目標相對于雷達視線的姿態不變，僅使得脈沖整體偏移，即產生的平動分量對成像分辨率并無貢獻，因此將目標的平動分量補償后得到如圖1(b)所示的ISAR等效轉臺模型。

設圖1(b)飛機中心為O ，在飛機內建立O XY坐標系，其中 X為方位向， Y為距離向。假設飛機上有一 J點，其坐標為( xp,yp)， 與坐標軸 X 夾角為θ,J 點與O 點之間的距離為偏移矢量 rp，觀測時間tm內飛機以恒定角速度ω 勻速轉動，初始時刻飛機與雷達的斜距距離參考矢量為 R0。ISAR觀測雷達與目標一般相距較遠，滿足遠場假設，因此根據矢量相加可得雷達與J 點之間的距離為

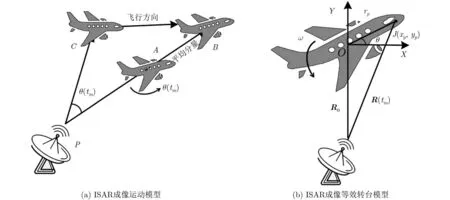
圖1 ISAR目標運動示意圖

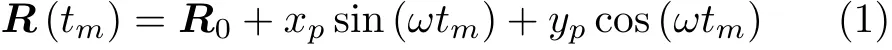
當ISAR成像積累時間較短時，滿足小轉角假設，即sin(ωtm)≈ωtm, c os(ωtm)=1，代入式(1)即可得雷達與J 點的瞬時距離為R (tm)≈R0+xpωtm+yp，地基雷達發射線性調頻信號，并采用dechirp模式接收回波，在經過包絡對齊和初相校正等處理流程后[11]，得到ISAR數據域p 個點累積回波為

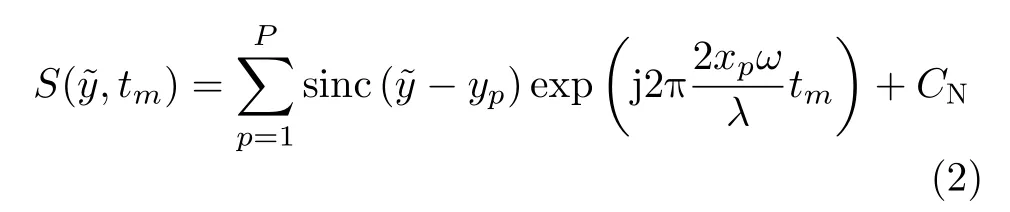
其中， sinc 函數為第p 個散射點的距離向包絡，exp函 數為方位線性相位項，λ 為雷達系統發射信號波長， CN為雜波與噪聲。觀察式(2)，可利用回波數據S (,tm)， 距離向包絡s inc函數和方位向線性相位，以及噪聲雜波 CN項建立其對應矩陣形式的線性回歸模型

其中， Y ∈CN×M對應式(2)中的S,tm)，表示距離壓縮預處理后方位向和距離向分別為 N與 M的回波數據。 X ∈CN×M為待恢復的高分辨雷達數據，CN為加性的噪聲干擾等。 A為方位向傅里葉表示字典。

3 穩健型雙層疊組LASSO-ADMM成像算法

求解如式(3)所示的回歸模型是數學上典型具有病態性的反問題，即其解未必滿足唯一性、穩定性和存在性，而通過引入需要的先驗信息來添加約束條件以構建正則化，便可使得問題良態化。經典的?1范數正則化[12](LASSO)定義如式(5)所示

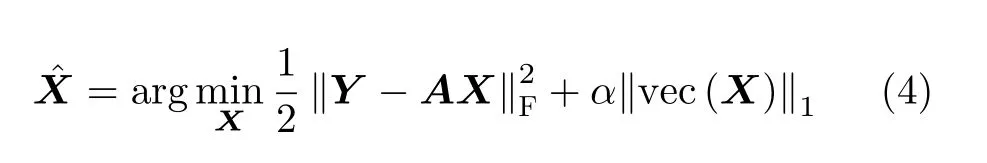
其中，‖ ·‖F為Frobenius范數(?F范數)，‖ ·‖1為 ?1范數， α>0為正則項調節參數，可以控制對數據施加懲罰的程度。v ec(·)為向量化算子，用于2維雷達回波信號的向量化。式(4)中第1項為數據保真項，使得在稀疏懲罰強弱變化時保證重建成像結果與原始目標場景圖的逼近程度，第2項為正則先驗項，用以限制解空間，表征SAR成像場景中強散射點的稀疏先驗信息。但是LASSO模型具有一定的局限性，該模型中僅引入了目標的稀疏先驗信息，在稀疏恢復過程中很容易丟失目標的弱散射特征，導致精細的結構特征無法保留下來，從而影響ISAR成像的恢復精度。因此本文提出一種穩健型雙層疊組LASSO(Robust and Two-tier Group LASSO,RTGL-LASSO)回歸模型如式(6)所示

3.1 更新 X變量

對式(8)中第1步 X變量的更新迭代過程，設目標函數為

3.2 更新分裂變量 Z 及對偶變量U

在式(8)第2步分裂變量 Z 更新過程中，為實現對ISAR回波復數據的組水平稀疏和結構平滑效果，RTGL-ADMM算法采用從方位向和距離向進行雙層疊分塊方式對變量 Z進行更新迭代。其中方位向是對每個回波采樣進行分組，其對應的鄰近算子為

總結RTGL-ADMM算法流程如表1所示。

4 實驗驗證

為驗證RTGL-ADMM用于ISAR高分辨成像的穩健性能等，本文利用ISAR系統仿真復數據以及Yak-42實測ISAR數據對所提RTGL-ADMM算法與傳統基于?1范數正則化模型的ADMM算法進行對比實驗，并應用相變曲線圖對兩種算法進行定量對比實驗，從而驗證所提算法在應用于ISAR高分辨成像 時優越的結構及稀疏恢復性能。

4.1 ISAR系統仿真復數據成像對比實驗

本實驗通過一組仿真合成的ISAR數據來驗證所提RTGL-ADMM算法的恢復性能，仿真實驗中雷達距離向分辨率為0.1 m，方位向分辨率為0.3 m，發射信號帶寬為1.5 GHz，脈沖重復頻率為100 Hz。圖2(a)所示為經過距離壓縮和距離徙動校正后得到的ISAR參考目標成像，圖中共有143個散射點，每個點的強度服從均值為2，方差為5的復高斯分布。圖2(b)為加入0 dB高斯白噪聲處理后的成像結果，圖2(c)為基于LASSO模型的ADMM算法成像結果，目標正方形的邊緣特征已經不清晰，內部的連續結構特征也幾乎未恢復，且背景噪聲仍存在，可見傳統的LASSO-ADMM算法在處理中擁有不可避免的局限性。圖2(d)為本文RTGL-ADMM算法成像結果，可見恢復后目標的散射強度與原圖相近，并且目標內部和邊緣結構恢復以及抑噪性能方面相較于圖2(c)具有明顯優越性。本仿真實驗有效驗證了RTGL-ADMM算法應用于結構特征增強時的良好成像性能。

表1 RTGL-ADMM算法流程

4.2 Yak-42實測數據成像對比實驗

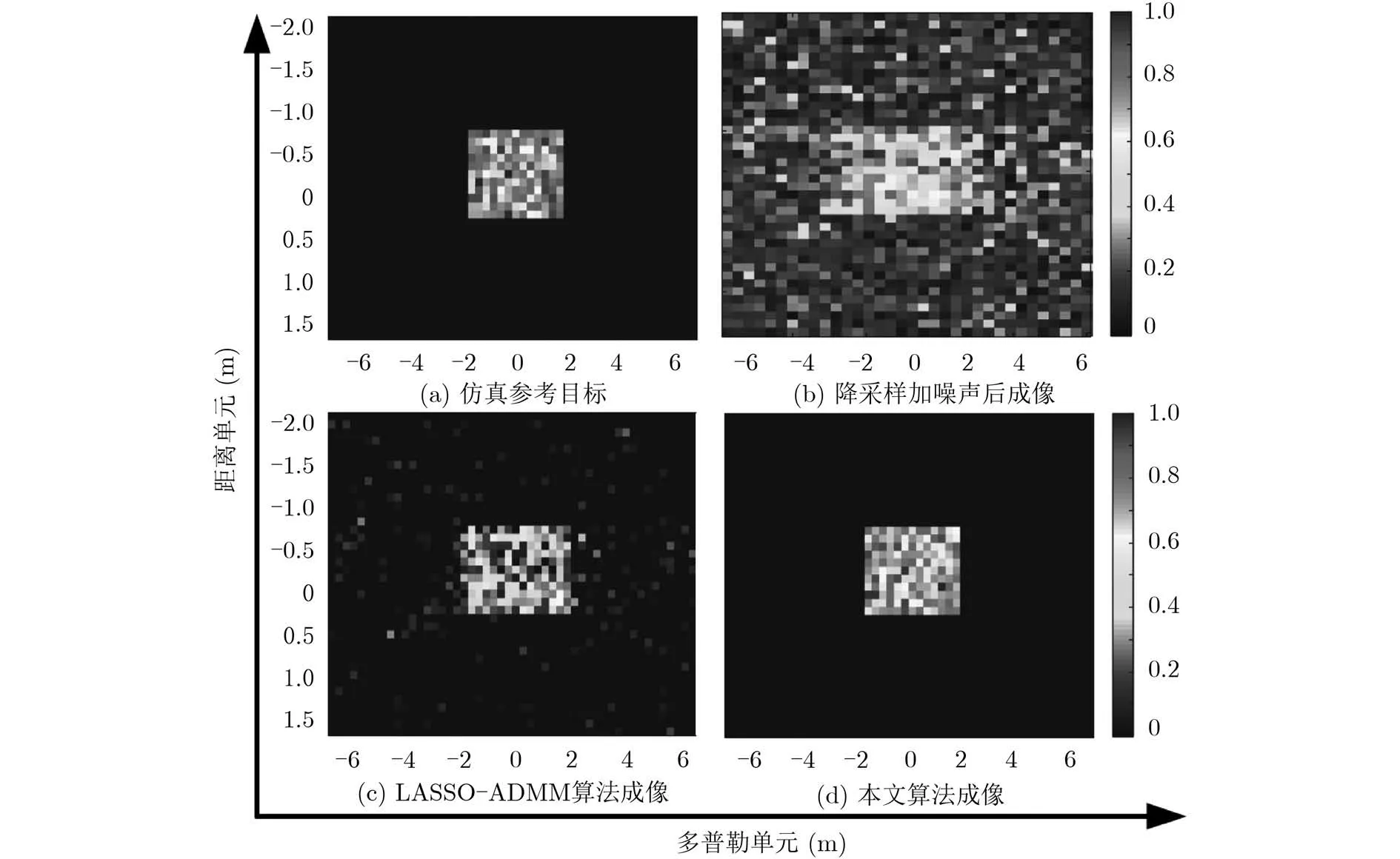
圖2 仿真ISAR復數據不同算法成像結果

圖3 固定降采樣時不同信噪比下不同算法成像結果對比

本組實驗采用Yak-42運輸機的實測ISAR數據進行對比實驗來驗證所提RTGL-ADMM算法的成像優勢。由于ISAR實測數據一般背景噪聲雜波等較少，因此為了驗證所提算法的穩健性，本文設置了兩組LASSO-ADMM算法和RTGL-ADMM算法在分別模擬加噪聲與降采樣情況下的成像對比實驗，結果如圖3與圖4所示。圖3所示為固定降采樣(UnderSampling Radio, USR)為0.5條件下，信噪比(Signal to Noise Ratio, SNR)分別為5, 0以及–2 dB時不同算法成像對比實驗。第1行為距離多普勒(Range Doppler, RD)算法直接成像結果，可見隨著信噪比的降低，噪聲不斷增加，目標幾乎已被噪聲覆蓋。第2行為LASSO-ADMM算法處理后結果，相較于RD算法，LASSO-ADMM算法的去噪效果明顯，但為了保證飛機結構不大幅度丟失，LASSO的正則化約束參數并未過大過于稀疏，使得成像效果不夠理想。第3行為本文RTGL-ADMM算法處理結果，本文算法的飛機結構飽滿度大于LASSO-ADMM算法，特別是機翼和機身部分對比強烈。第3列信噪比為–2 dB時同樣類似，雖然本文算法此時存在部分噪聲，但結構恢復以及稀疏效果都強于LASSOADMM算法。

圖4所示為固定信噪比為5 dB條件下降采樣分別為1, 0.5, 0.25時LASSO-ADMM算法和本文所提算法的成像對比實驗。同樣可看出本文算法在降采樣率降低的情況下，成像效果仍然強于LASSOADMM算法，因此圖3與圖4實驗有效定性分析了本文算法在不同信噪比不同降采樣率下結構特征增強成像的穩健性。

4.3 相變曲線圖對比實驗

圖4 固定信噪比時不同降采樣下不同算法成像結果對比

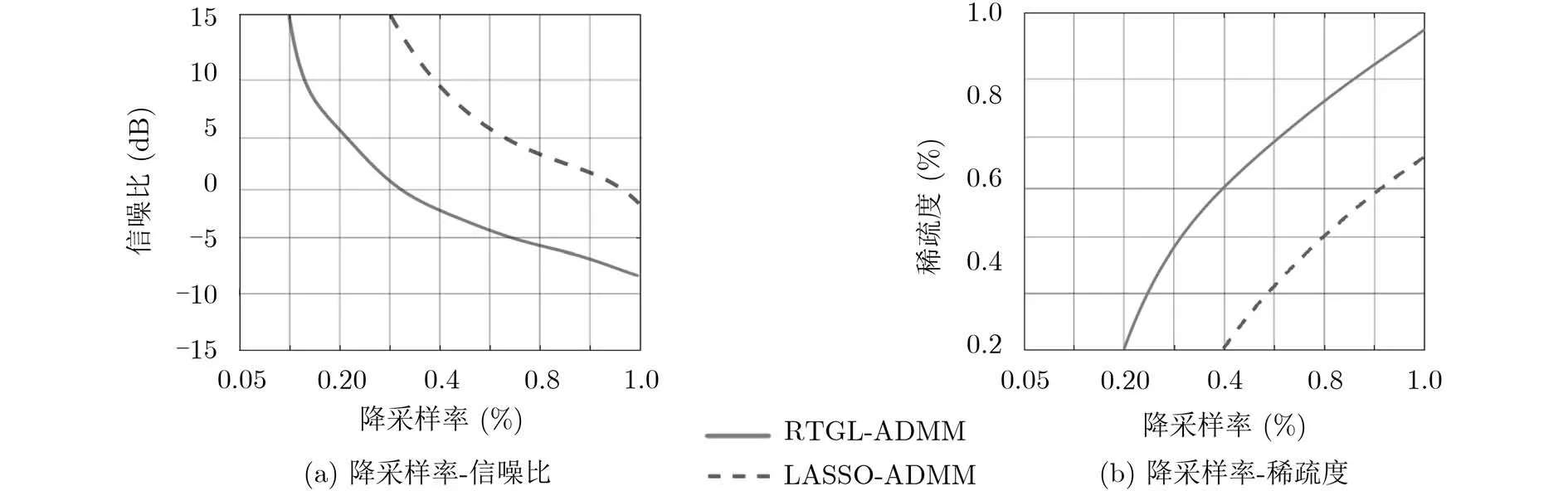
圖5 兩種算法相變曲線圖對比

本組實驗中引入相變曲線圖來更清晰地進一步定量評估所提算法用于ISAR成像的恢復性能。相變曲線圖分析法由Donoho等人[13]提出。本文采用圖2所示的仿真ISAR數據進行蒙特卡洛實驗。如圖5所示為LASSO-ADMM算法與本文算法的降采樣率-信噪比相變曲線圖，橫軸為降采樣率，降采樣率的變化范圍為0.05%～1.0%。縱軸為信噪比，其變化范圍為–15～15 dB，曲線圖通過計算算法在不同參數條件下恢復成像結果與仿真參考成像圖的相關度來衡量算法的恢復性能，圖5(a)中右上角為對應參數性能最佳的點，越靠近右上角部分的面積越大則代表能夠恢復的區域越大，相關度越強，反之越靠近左下角則表示相關度越接近0，成像效果越差，因此通過判斷相變曲線所占范圍即可比較不同算法間的恢復性能差距，明顯本文算法的降采樣率-信噪比相變曲線圖范圍更大。圖5(b)為LASSOADMM與本文算法的降采樣率-稀疏度相變曲線圖，其中縱軸為信號的稀疏度，在本實驗中，右下角為橫縱軸對應參數下性能最佳的點，越靠近右下角則代表相關度越大，可看出本文算法的相變曲線靠近右下角所占的面積大于傳統算法，因此圖5(a)和圖5(b)兩種相變曲線圖利用3種參數下兩種算法的恢復性能定量評估對比，有效驗證了本文算法的成像優勢。

5 結論

本文針對傳統基于?1范數正則化的ADMM算法在ISAR成像中僅能增強稀疏特征，從而容易丟失目標精細結構特征影響最終高分辨成像精度的問題，研究建立了穩健型雙層疊組LASSO模型，將距離向和方位向分別分組層疊后應用ADMM框架，對 ?F范數對應的鄰近算子迭代求得其閉合解，形成組間稀疏與組內平滑，從而實現對ISAR的組稀疏與結構特征增強成像。實驗部分利用仿真和實測數據定性分析，以及相變曲線圖定量評估共同驗證本文算法應用于ISAR成像的有效性、優越性以及穩健性。