彈道中段不同平動多目標的平動參數估計方法

馮存前 李 江 黃大榮 胡曉偉 韓立珣

(空軍工程大學防空反導學院 西安 710051)

1 引言

近年來隨著分導式多彈頭及誘餌干擾等突防技術的發展[1]，基于傳統特征的識別技術失效，戰略預警和反導作戰面臨嚴峻考驗，而微動特征作為目標固有運動屬性為彈道目標識別提供了一種有效途徑[2]。現有許多微動特征提取、參數估計及微動分類[3–7]的文獻都是基于平動已得到較好補償的前提下進行的，但群目標技術的發展使得彈道目標的平動補償更為復雜，有待進行更深入的研究。

對于彈道中段目標的平動補償方法國內外學者進行了廣泛研究，大致可分為以下3種：(1)基于多普勒頻譜信息。文獻[8]提出了頻譜重排法，對平動1階加速度進行了估計，但此方法易受噪聲影響；文獻[9]提出一種分段平動補償方法，通過使回波頻譜熵最小化，在時頻混疊的情況下有效地估計了加速度和速度。(2)基于時頻分析。文獻[10]利用目標的整體信息，采用Radon變換檢測時頻曲線傾斜度，結合最小熵準則和高斯模板函數對變換域進行峰值搜索實現平動參數估計。文獻[11]通過改進的Harris角點檢測算法提取出時頻曲線的交點信息，完成平動參數估計進而實現平動補償。但是此類方法在受到噪聲嚴重污染時因無法進行圖像特征的有效提取而性能急劇下降。(3)基于信號處理。文獻[12]利用微多普勒信號的周期性進行延遲共軛相乘消除微動信號，然后等效為多項式相位信號參數估計問題實現平動2階加速度和1階加速度的估計；文獻[13,14]則利用進動目標微多普勒信號的對稱性，通過對稱共軛相乘消除微動分量后進行傅里葉變換，搜索頻譜峰值信息估計平動加速度和速度。此外還可通過構造冗余的微動原子集來估計平動速度和微動參數[15]，但僅適用于具有正弦形式的微動信號。

以上分析中，所采用的2階多項式等效平動[8–11,13–15]的方法將會影響最后的補償效果。此外，目前所進行的研究都是基于單目標或同一平動的群目標的情況，但對于更貼近實際的具有不同平動參數的多目標情況還沒有相關方面的報道，因此有必要開展相關研究。

針對處理多目標問題，傳統的思路都是先進行分離預處理，然后再進行參數估計，但此類方法過程繁瑣且運算量大。本文考慮到彈道目標的平動補償問題實際上是一個多項式參數估計過程，而高階模糊函具有運算量小、估計階數高及精度高等優勢[16]，因此可應用于多目標平動補償問題中；此外，考慮到周期信號進行延遲共軛相乘處理后，可在其頻譜處出現峰值，而彈頭目標的微動正是周期運動；最后，利用時頻分布的差異進行時間維度的加權累加可實現速度估計。仿真結果驗證了所提方法的有效性和低噪聲條件下的魯棒性。

2 復合運動模型

彈道群目標中，主要包括彈頭、輕重誘餌、彈體碎片及燃料箱等，其中：燃料箱和碎片等可利用形態加以區別，因此本文將針對真假彈頭組成的多目標進行平動分析研究。

2.1 回波模型分析

假設雷達發射波長為 λ的單頻信號，則雷達接收到多目標的基頻回波信號為

2.2 平動距離分析

首先利用觀察時間內的某個脈沖測得速度 vi′對速度進行粗補償[14]，可解決微多普勒時頻圖的折疊現象，補償后的平動速度為? vi。同時在較短的觀察時間內，平動分量可近似為3階多項式[12]，則t 時刻粗補償后的平動距離為

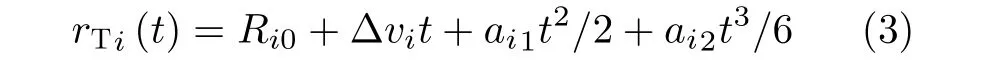
其中，Ri0, ai1, ai2分別為第i 個目標的初始徑向距離 、1階加速度、2階加速度。

2.3 微動距離分析

由暗室測量實驗知，彈道進動錐體目標其后向散射主要由錐頂 A和錐底滑動散射中心 B, C決定，如圖1所示，其中：O ?XY Z是與雷達坐標系平行的參考坐標， O ?xyz為目標本地坐標系，原點O為目標質心，O x為目標對稱軸。在圖1(a)的錐體彈頭進動模型中，對稱軸O x 與錐旋軸O Z的夾角為進動角 θ ，且O x 軸初始時刻在O xy平面的投影與OX 軸的夾角為初始錐旋角φ0，記初始時刻雷達視線方向L OS與O Y Z 共面，且與錐旋軸O Z、對稱軸Ox 的夾角分別為α, β。

由圖1(a)可知，進動目標各散射點的微動距離為

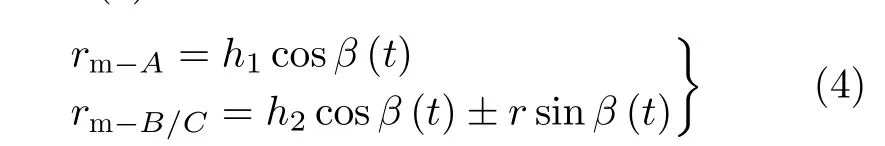
圖1 微動模型

3 多目標平動參數估計方法

3.1 基于高階模糊函數的2階加速度及微動周期估計

回波的3階矩函數可表示為

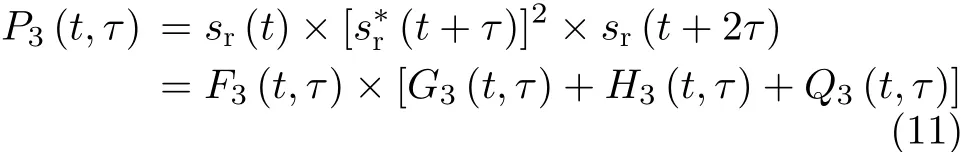
其中，

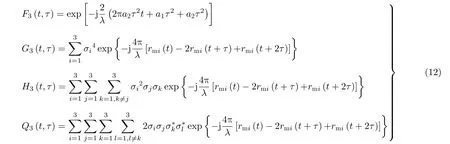
3.2 基于延遲共軛相乘的1階加速度估計

交叉項在頻域能量分散，對局部峰值位置影響不大。同理，對式(16)進行傅里葉變換，其余項頻域能量分散，頻譜峰值保持位置不變，即在多目標多散射點的情況下，其頻譜僅是對應噪聲基底增加，但局部峰值仍然明顯。

3.3 基于時頻分布的平動速度補償

在補償后的i ×j條目標回波時頻圖曲線中，將會表現為某一目標散射點對應的 j 條曲線被“拉平”，而其它目標散射點對應的曲線將會有不同程度的傾斜；被“拉平”的j 條曲線一個周期內存在兩個能量較大的交點，且交點處曲線趨勢變化快。

基于以上分析，我們將補償后的回波時頻曲線沿著時間橫坐標進行累加處理。但由于時頻曲線中存在其它能量強點，如：該 j條曲線的極值點位置附近的點、其它時頻曲線的交點，這些點的存在將會對直接累加后的效果產生干擾。在整個觀察周期內：該 j條曲線交點處所對應的這一行時頻矩陣，具有多個能量強點，且交點處曲線斜率更大，使得能量強點的持續時間短。相比之下，其它曲線交點僅是個別強點；單曲線極值點位置附近的點能量相對較低，且曲線平緩，強點持續時間更長。即j 條曲線交點所對應位置處的時頻矩陣數據，因具有多個持續時間短的能量強點，將會在其頻譜上表現為：在更多的分頻通道上分布能量較大的點。因此，將不同分頻通道上的能量進行累加，該交點所對應的縱坐標處會出現最大值，從而實現對第i 個目標的平動速度的估計。具體操作如下：

4 仿真分析

為驗證本文方法的有效性，進行如下仿真。設錐體參數為：質心到錐頂、錐底的距離分別為h1=1.125 m, h2=0.375 m ，底面半徑r =0.252 m，目標散射數據由物理光學法獲得。微動參數為：進動時，進 動 角 θ =10?，錐 旋 角 速 度ωc=6 rad/s，初始錐旋角 φ0=10?，雷達視線與錐旋軸α =45?；擺動時，擺動角幅度 θ1=10?，初始擺動角θ0=30?， 擺動角速度ωs=8 rad/s。雷達參數：發射載頻 f0=10 GHz ，脈沖重復頻率P RF=1 kHz，觀察時間T =4 s ，信噪比為5 dB，考慮遮擋效應。

設雷達目標回波中包含1個錐體彈頭和1個錐體誘餌，目標平動參數為：彈頭， ?v1=?4 m/s,a11=1.5 m/s2, a12=0.5 m/s3； 誘餌? v2=?1.5 m/s,a21=0.8 m/s2, a22=0.25 m/s3。圖2(a)為雷達目標回波的時頻圖，圖2(b)為目標回波的3階模糊函數，可得到明顯的兩個獨立峰值。考慮到彈頭的進動周期明顯比誘餌的擺動周期長，因此可在“峰值搜索-去除峰值”過程中，以第1個目標“主峰值”為圓心，以? r′為半徑，將此圓范圍內的點進行置零處理。設置搜索的時間步長為 ?t′=2/PRF,?r′=50(局部峰值數量)。

需要說明的是，模糊函數的時間搜索步長?τ對參數的估計影響較大，原因在于當被估計周期不是 ?τ的整數倍時，該周期處的峰值將會被搜索“跳過”，從而產生較大誤差。本文經過多次仿真實驗表明：仿真時間相差不大的前提下只要保持?τ ≤0.004 s，估計參數仍然有效。因此可以選擇較小的? τ 來減小估計誤差，本文選取? τ =2/PRF。

接下來，我們對不同信噪比條件下參數估計的效果進行100次蒙特卡洛仿真。定義其歸一化均方根誤差(Normalized Root Mean Square Error,NRMES)為

圖2 目標混合回波

圖3 延遲共軛相乘后的頻譜圖

不同參數在不同信噪比條件下的NRMES如圖5所示。分析知，當信噪比不低于3 dB時，平動參數能夠實現有效估計；當信噪比低于3 dB時，由于噪聲干擾增大，一個目標的峰值搜索出現較大誤差，但另一個目標仍能實現有效估計；由于其它時頻曲線交點的干擾，目標的平動速度估計誤差相對較大。

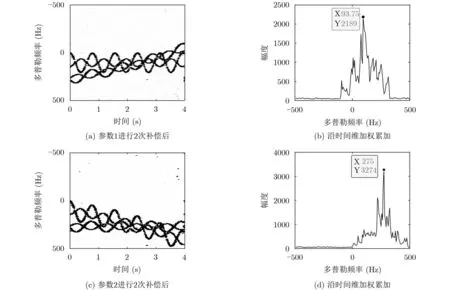
圖4 剩余平動速度估計

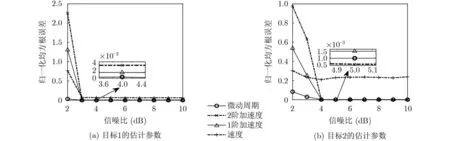
圖5 參數估計值的蒙特卡洛仿真

表1 多目標同平動參數的估計性能

為進一步驗證本文方法的有效性，分別與文獻[10,11]進行多目標、單目標同平動參數估計對比，表1，表2給出100次蒙特卡羅仿真的對比結果，圖6—圖8為其使用方法。

由表1，表2知，與文獻[10,11]相比本文方法精度更高，分析如下：(1)與文獻[10]相比，Radon變化僅能對整體時頻圖趨勢進行直線擬合，這與實際曲線產生較大誤差，而本文方法采用高階多項式進行估計，因此精度更高；(2)與文獻[11]比較，角點檢測存在個別錯誤角點影響最終的擬合效果，并且當信噪比降低時角點檢測錯誤率更高，而本文是利用信號延遲共軛相乘后自項能量高的特性，能更好地降低信噪比的影響，魯棒性更強。

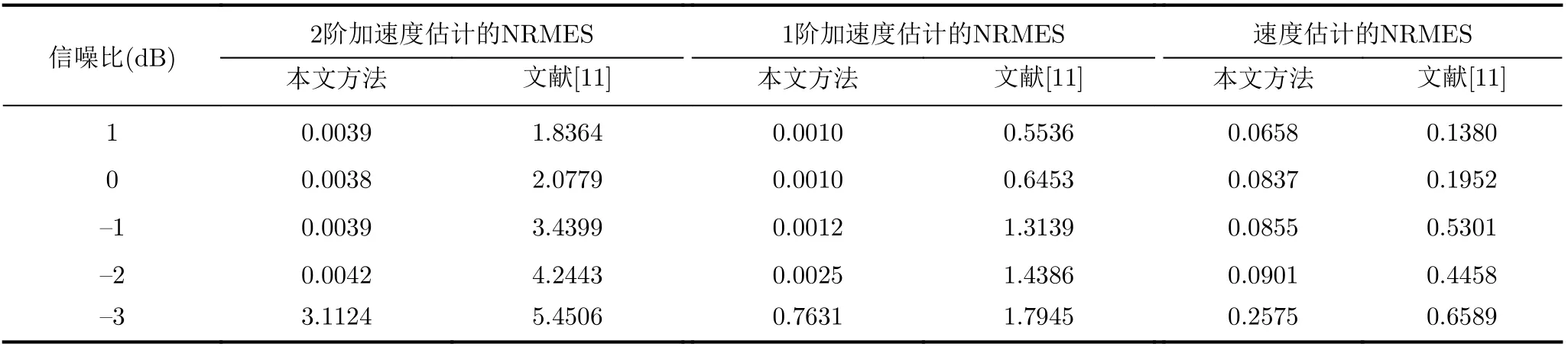
表2 單目標平動參數的估計性能

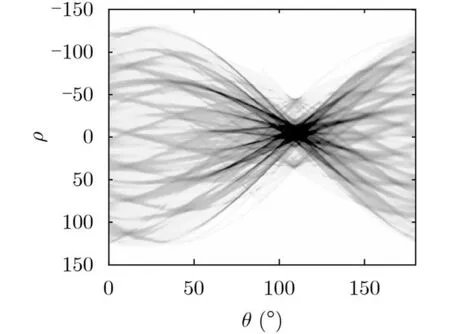
圖6 文獻[10]采用的Radon變換

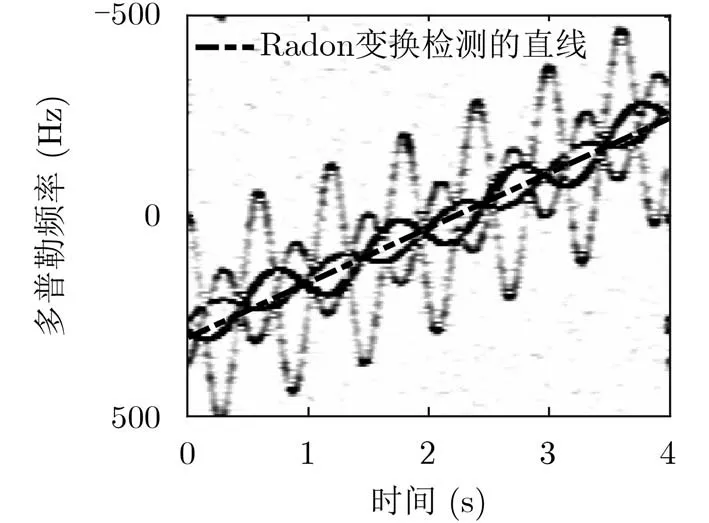
圖7 文獻[10]檢測到的平動直線

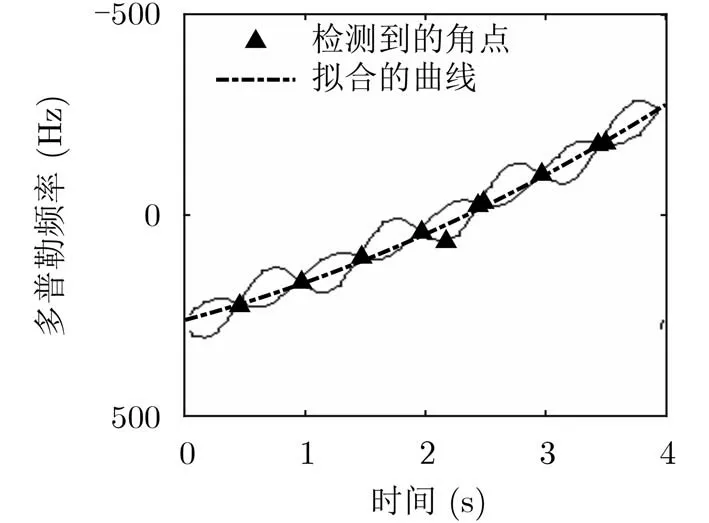
圖8 文獻[11]檢測到的角點和擬合曲線

5 結束語

多目標雷達回波信號是多個分量的疊加，想要直接分離比較困難。本文采用高階模糊函數通過峰值搜索完成逐次估計，并結合時頻分析，可在不分離信號的前提下直接實現平動參數和微動周期的高精度估計，為彈道目標的參數估計和識別提供重要基礎。

本文方法實質上是利用了微動信號的周期性，通過延遲共軛相乘消除或降低微動的影響來估計平動參數，因此可用于分析兩個以上的目標，為彈道群目標的平動補償提供一種思路。但是，多目標回波信號的延遲共軛將會導致處理后的回波信噪比降低，致使噪聲魯棒性變弱，且更多的時頻曲線交點也會影響平動速度估計的效果，這也將是下一步研究的重點。