基于序列密碼的圖像加密算法

胡超飛，尹毅峰，劉琨鵬

(鄭州輕工業(yè)大學(xué) 計(jì)算機(jī)與通信工程學(xué)院，鄭州 450002)

伴隨著現(xiàn)代社會(huì)多媒體等技術(shù)的發(fā)展，信息化社會(huì)越來越成熟.但是隨著信息化社會(huì)帶來的問題是信息的安全，人們?cè)絹碓疥P(guān)注信息安全,信息的傳輸安全顯得尤其重要.相比傳統(tǒng)的文字等信息，多媒體社會(huì)的信息載體多種多樣，例如：聲音、圖像、視頻等.新的信息載體包含著更大量的信息，所以對(duì)信息安全的要求也更高[1]，人們?cè)谶M(jìn)行信息的傳輸時(shí)，都希望自己傳輸?shù)男畔⒉粫?huì)被他人竊取和篡改，確保自己傳輸?shù)膬?nèi)容完整并且具有保密性.在現(xiàn)在的社會(huì)中，通信過程中使用最為廣泛的信息載體就是圖像，一是因?yàn)閳D像作為信息載體包含的信息量巨大，能夠生動(dòng)形象的描述想傳達(dá)的信息，例如在國(guó)防、社會(huì)、私人和航空航天網(wǎng)絡(luò)中，圖像信息就是最頻繁的一種通信形式;二是圖像信息傳輸是如今最方便使用的手段之一,正是因?yàn)槭褂昧看螅⑶沂褂梅奖悖詧D像信息傳輸?shù)陌踩跃托枰叩囊骩2].

圖像信息安全性的需求提高，本文就是針對(duì)圖像為載體的信息加密進(jìn)行研究.圖像數(shù)據(jù)由于其信息量較大，所以加密難度較高.傳統(tǒng)的對(duì)稱性加密的安全性不夠高，非對(duì)稱加密的加密效率對(duì)于信息量較大的圖像效率較低.本文提出的圖像加密在加密安全性能方面有著較大的優(yōu)勢(shì).使用序列密碼[3]結(jié)合混沌映射理論的優(yōu)勢(shì)提出的圖像加密算法能夠使一些較為隱私的圖片安全地進(jìn)行傳輸.

隨著科技的發(fā)展，各行業(yè)各領(lǐng)域的科技都在創(chuàng)新，圖像加密也有著很多創(chuàng)新[4]，例如：有著很多其他領(lǐng)域的知識(shí)都被應(yīng)用到圖像加密技術(shù)的研究中，并且因?yàn)橐昧似渌I(lǐng)域的知識(shí)來豐富圖像加密的內(nèi)容[5]，所以有著許多新穎的圖像加密方法被提出.Enayatifar等[6]將極大堆積樹的理論應(yīng)用在圖像加密算法中，在置亂效果上有著顯著的成果，算法安全性也較高，想法新穎獨(dú)特，但計(jì)算復(fù)雜度卻很高.Abdullah等[7]使用生物學(xué)中的遺傳算法與Logistic混沌相結(jié)合對(duì)圖像進(jìn)行置亂，大幅度的降低了圖像的像素相關(guān)性.有很多成熟的圖像加密技術(shù)應(yīng)用在計(jì)算機(jī)端了，也有一些創(chuàng)新的圖像加密算法也有比較好的效果，但是目前社會(huì)在移動(dòng)端上的圖像加密方面還是沒有太多建樹，計(jì)算機(jī)端的一些加密算法通常需要很高的計(jì)算復(fù)雜度，對(duì)于當(dāng)前社會(huì)的實(shí)際價(jià)值并不高,所以又有學(xué)者通過將混沌系統(tǒng)與其他加密技術(shù)相結(jié)合來對(duì)圖像進(jìn)行加密[8-10]，增加了圖像加密的復(fù)雜性，顯著的提髙了其安全性.文獻(xiàn)[11]中提出了一種自編碼，混沌和超混沌映射相結(jié)合的一種新的圖像加密算法，與上述加密算法相比此類算法不僅提高了圖像加密的安全性還增加了加密效率[12].莊志本等[13]對(duì)混沌系統(tǒng)進(jìn)行改進(jìn)，提出了一種高維混沌的圖像加密算法能夠有效地抵御統(tǒng)計(jì)分析攻擊和灰度值分析攻擊.

綜合近年來學(xué)者的研究，對(duì)于輕量級(jí)的圖像加密[14]方法的研究不多.但是輕量級(jí)的圖像加密算法[15-16]卻越來越重要，輕量級(jí)的加密不僅僅適用于PC端，還能夠適用于移動(dòng)終端，能夠提升移動(dòng)終端的圖像傳輸?shù)陌踩?本文結(jié)合序列密碼中的m序列以及對(duì)稱密碼學(xué)的經(jīng)典加密算法希爾密碼對(duì)圖像進(jìn)行加密，并且結(jié)合混沌置亂的方法提出的加密方法，通過m序列增強(qiáng)加密算法的密鑰安全性，結(jié)合傳統(tǒng)的希爾加密，能夠快速并且安全地對(duì)圖像進(jìn)行加密.

1 基于序列密碼的圖像加密算法描述

1.1 預(yù)備知識(shí)

希爾密碼是運(yùn)用矩陣論基本運(yùn)算的一種替換密碼，在1929年被Lester S.Hill發(fā)明.它的原理就是將26個(gè)英文字母看作0～25個(gè)數(shù)字，例如：A=0，B=1，C=2，…，然后每一串字母都看作是一個(gè)n維向量，通過一個(gè)可逆矩陣與n維向量進(jìn)行矩陣的乘法運(yùn)算得出一個(gè)數(shù)值，該數(shù)值對(duì)26進(jìn)行取模運(yùn)算以后的結(jié)果就是密文數(shù)字，密文數(shù)字對(duì)應(yīng)的字母就是密文.解密過程就是將加密的密鑰矩陣進(jìn)行求逆運(yùn)算，然后將密文數(shù)字和密鑰矩陣的逆矩陣進(jìn)行相乘得出的結(jié)果和26進(jìn)行取模運(yùn)算就能夠得出原文.

本文使用希爾密碼的理論對(duì)圖像進(jìn)行加密，使用的是灰度級(jí)為256的圖像，每個(gè)像素的像素值最大為256，把每一個(gè)像素值當(dāng)作256進(jìn)制數(shù)字，每一個(gè)像素值與密鑰矩陣相乘的結(jié)果mod256得出的數(shù)字對(duì)應(yīng)的像素就是密文.

1.2 基于序列密碼的圖像加密原理

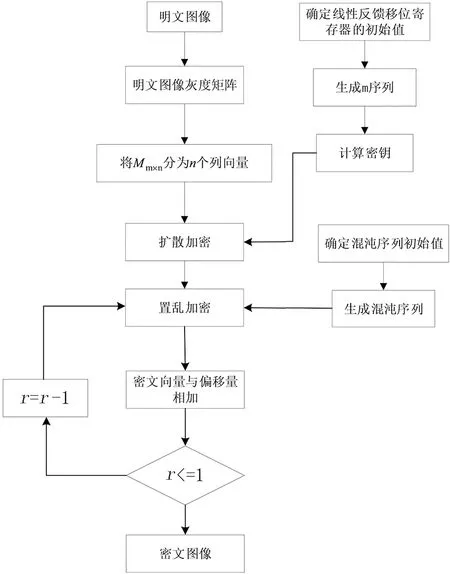
圖1 基于序列密碼的圖像加密算法加密過程Fig.1 The encryption process of image encryption algorithm based on sequence cipher

1.3 算法加密過程

步驟1 選取灰度級(jí)為256的明文圖像，然后讀取圖像Pm×n，通過灰度矩陣轉(zhuǎn)換算法求出圖像Pm×n的灰度共生矩陣Mm×n.

步驟2 通過線性反饋移位寄存器生成一個(gè)m序列，計(jì)算出序列的線性復(fù)雜度L，確定m序列中的任意2L-1長(zhǎng)的一段序列(SiSi+1Si+2…Si+2L-2)以及確定算法的平移量x0.

步驟3 將灰度矩陣Mm×n分成n個(gè)列向量(γ1,γ2,γ3,…,γn)，然后根據(jù)周期序列的性質(zhì)以及確定的序列段(SiSi+1Si+2…Si+2L-2)求出可逆矩陣作為加密密鑰Ekey.

Mm×n?(γ1,γ2,γ3,…,γn).

(1)

(2)

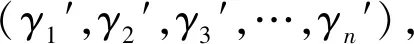
(3)

(4)

步驟5 對(duì)擴(kuò)散加密后的列矩陣組進(jìn)行置亂迭代r次，每迭代一次都將與偏移量x0進(jìn)行相加，最終得到向量組(γ1?,γ2?,γ3?,…,γn?)，密文矩陣通過聚合成為一個(gè)密文圖像進(jìn)行傳輸.

1.4 算法解密過程

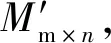
(5)

步驟2 通過可信信道獲得m序列，序列段(SiSi+1Si+2,…,Si+2L-2)以及算法的平移量x0，然后計(jì)算出線性復(fù)雜度L.根據(jù)線性復(fù)雜度L以及確定的序列段求出加密密鑰，然后加密密鑰通過矩陣運(yùn)算求出其逆矩陣，逆矩陣即為解密密鑰Dkey.

(6)

步驟3 列向量(γ1?,γ2?,γ3?,…,γn?)減去偏移量x0后進(jìn)行解密迭代，每進(jìn)行一次解密迭代都減去一次偏移量x0最終得到向量組(γ1″,γ2″,γ3″,…,γn″).

步驟4 根據(jù)希爾加密的原理，將步驟2中得到的解密密鑰Dkey對(duì)解密迭代的列向量進(jìn)行解密運(yùn)算得到(γ1,γ2,γ3,…,γn)，然后將列向量組(γ1,γ2,γ3,…,γn)轉(zhuǎn)化明文圖像.

(7)

(8)

Pm×n=(γ1‖γ2‖γ3…‖γn).

(9)

2 實(shí)驗(yàn)仿真結(jié)果

2.1 密鑰敏感性分析

密鑰敏感性是衡量一個(gè)算法密鑰安全性的指標(biāo).密鑰敏感性分析就是指在密鑰發(fā)生微小的改變后，改變后的密鑰作為解密密鑰進(jìn)行正常解密操作，如果一個(gè)算法的密鑰敏感性強(qiáng)，那么在密鑰變化極小的時(shí)候，密鑰也不能作為解密密鑰進(jìn)行正確的解密，如果算法的密鑰敏感性不強(qiáng)，那么解密密鑰在進(jìn)行微小的改動(dòng)后，改動(dòng)后的密鑰也能夠進(jìn)行解密操作.算法1的密鑰是通過線性反饋移位寄存器生成的m序列，然后確定m序列中的一段序列段，最后根據(jù)周期序列的性質(zhì)，通過序列段生成的矩陣作為密鑰.本文密鑰敏感性測(cè)試是通過改變1位m序列寄存器的初始值，然后使用相同操作生成密鑰對(duì)同一密文進(jìn)行解密，獲取解密圖像.實(shí)驗(yàn)結(jié)果如圖2所示.

圖2(a)為未加密的原圖，圖2(c)為使用正確密鑰進(jìn)行解密后的解密圖像，圖2(b)為將m序列寄存器的初始值進(jìn)行修改1位后生成的解密密鑰對(duì)密文圖像進(jìn)行解密的圖像.根據(jù)實(shí)驗(yàn)結(jié)果可知，圖2(b)中無法觀察到圖像信息，實(shí)驗(yàn)證明及其微小的改動(dòng)也能夠使得改動(dòng)后的密鑰沒法對(duì)密文圖像進(jìn)行解密.所以證明算法1的密鑰敏感性較強(qiáng).

(a) (b) (c)圖2 密鑰敏感性實(shí)驗(yàn)結(jié)果Fig.2 The key sensitivity experiment results

2.2 抗差分攻擊

抗差分攻擊能力是評(píng)定算法安全性的一個(gè)重要的因素，一個(gè)安全的圖像加密算法應(yīng)該有著良好的抗差分攻擊能力.一般對(duì)圖像加密來說，通常使用兩種標(biāo)準(zhǔn)來衡量一個(gè)這個(gè)算法對(duì)圖像加密的抗差分攻擊能力，這兩種標(biāo)準(zhǔn)分別是像素變化率NPCR(Number of Pixels Change Rate)和歸一化像素值平均改變強(qiáng)度UACI(Unified Average Changing Intensity).像素變化率和歸一化像素值平均改變強(qiáng)度的計(jì)算公式為:

(10)

(11)

(12)

其中C1,C2分別是兩幅大小都為(M,N)的灰度圖像.

根據(jù)計(jì)算可知NPCR的理論值為0.996 1，UACI的理論值為0.334 6，經(jīng)過多次測(cè)試以后取平均值與文獻(xiàn)[17]中的算法2和文獻(xiàn)[18]中的算法3對(duì)比得知，算法1測(cè)量后的平均值與相關(guān)文獻(xiàn)結(jié)果相當(dāng)，所以算法1能抵抗差分攻擊.實(shí)驗(yàn)結(jié)果如表1所示.

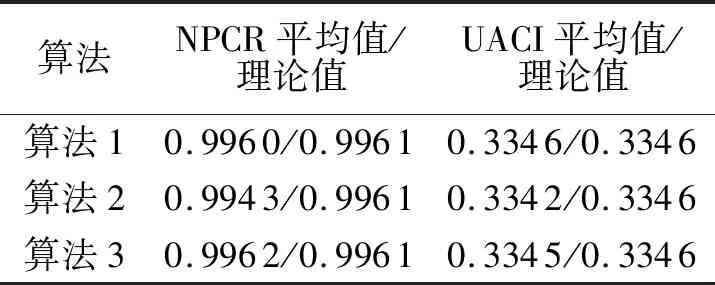
表1 抗差分攻擊實(shí)驗(yàn)結(jié)果Tab.1 The experimental results of resisting differential attack

2.3 信息熵

信息熵的概念是在香農(nóng)信息論中被提出的，信息熵用來表示平均信息量的一個(gè)指標(biāo)概念，反映了信源的不穩(wěn)定度，其公式為：

(13)

對(duì)密文圖片進(jìn)行信息熵的測(cè)量，如果任意像素出現(xiàn)的概率是均勻的話，這種情況下密文圖片是最混亂的，信息熵也是最大的.在這種情況下，信息最不容易泄露.圖像信息熵又叫圖像熵，是一種特征的統(tǒng)計(jì)形式.Si為密文圖像中灰度值為i的像素出現(xiàn)的比例，P(Si)則是密文圖像中像素值為i出現(xiàn)的概率.像素值出現(xiàn)的概率可以通過圖像的灰度直方圖獲取.本文使用的是灰度級(jí)為256的圖像，信息熵值的理論值為8，實(shí)驗(yàn)測(cè)量結(jié)果如表2所示.

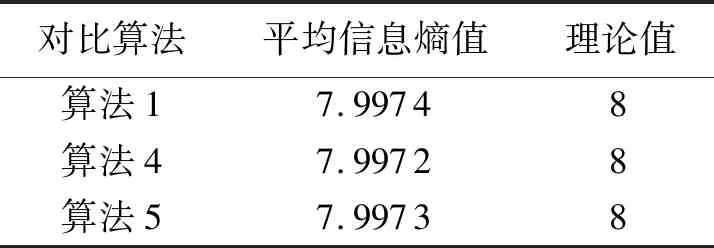
表2 信息熵測(cè)量結(jié)果Tab.2 The image entropy measurement results

通過實(shí)驗(yàn)表明，算法1的信息熵相比于文獻(xiàn)[19]中的算法4和文獻(xiàn)[20]中的算法5更接近8，所以算法1加密后的圖像信息相比算法4和算法5加密后的信息是更加無序混亂的，所以圖像信息更為安全且不容易泄露.

3 結(jié)語(yǔ)

本文提出的是一種基于序列密碼的加密算法.在將圖像灰度化的基礎(chǔ)上，利用序列密碼的特性以及混沌映射理論對(duì)圖像的矩陣進(jìn)行加密并且給出了相對(duì)應(yīng)的解密步驟.算法具有計(jì)算簡(jiǎn)單，對(duì)密鑰敏感等特點(diǎn)，并且m序列能夠增大序列周期，周期擴(kuò)大以后就能夠增大密鑰空間，使算法更安全.并且通過對(duì)其密鑰敏感性，抗差分攻擊以及信息熵等方面進(jìn)行了實(shí)驗(yàn)測(cè)試證明了該加密算法適合如今社會(huì)發(fā)展.