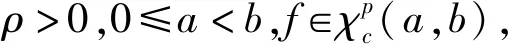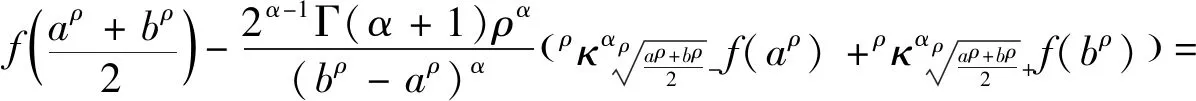基于katugampola分?jǐn)?shù)階積分的Hermite-Hadamard型不等式

海旭冉，王淑紅

(內(nèi)蒙古民族大學(xué) 數(shù)理學(xué)院，內(nèi)蒙古 通遼 028000)

分?jǐn)?shù)階微積分是研究任意階導(dǎo)數(shù)和積分的一門應(yīng)用數(shù)學(xué)學(xué)科，是和微分學(xué)一起誕生的古老學(xué)科，可以被看作是整數(shù)階微積分的超級(jí)組合，可以處理很多整數(shù)階微積分所不能處理的問題.分?jǐn)?shù)階微積分作為一種非常有用的工具，到現(xiàn)在為止不存在一個(gè)統(tǒng)一的定義，學(xué)者們從各自不同的角度入手，給出了分?jǐn)?shù)階微積分的幾種不同形式的定義，如經(jīng)典的Riemann-Liouville分?jǐn)?shù)階微積分、Caputo分?jǐn)?shù)階微分算子、Hadamard分?jǐn)?shù)階積分、調(diào)和分?jǐn)?shù)階積分、Katugampola分?jǐn)?shù)階積分等，其定義的合理性與科學(xué)性已經(jīng)在實(shí)踐中得到檢驗(yàn)，在科學(xué)、工程、數(shù)學(xué)和經(jīng)濟(jì)等領(lǐng)域幾乎都有實(shí)際應(yīng)用和深遠(yuǎn)影響[1-2].近年來，利用各類分?jǐn)?shù)階微積分，推廣凸函數(shù)和廣義凸函數(shù)的經(jīng)典不等式的問題備受關(guān)注，并成為研究熱點(diǎn)[3-5].本文在此基礎(chǔ)上，利用Katugampola分?jǐn)?shù)階積分，對(duì)擬凸函數(shù)及Hermite-Hadamard 不等式進(jìn)行研究，得到了一些新的積分不等式，推廣了Riemann-Liouville分?jǐn)?shù)階積分的相關(guān)結(jié)論.

1 預(yù)備知識(shí)

1.1 Riemann-Liouville分?jǐn)?shù)階積分

定義1[1]設(shè)(a,b)為實(shí)數(shù)軸R上的區(qū)間，其中a0，α是一個(gè)復(fù)數(shù)，則：

(1)

和

(2)

分別稱為左邊和右邊的Riemann-Liouville分?jǐn)?shù)階積分，其中Γ(·)為伽馬函數(shù)，

1.2 Hadamard分?jǐn)?shù)階積分

定義2[2]設(shè)(a,b)為實(shí)數(shù)軸R上的區(qū)間，其中a0，α是一個(gè)復(fù)數(shù)，則：

(3)

和

(4)

分別稱為左邊和右邊的Hadamard分?jǐn)?shù)階積分，其中Γ(·)為伽馬函數(shù).

1.3 Katugampola分?jǐn)?shù)階積分

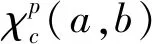
其中：

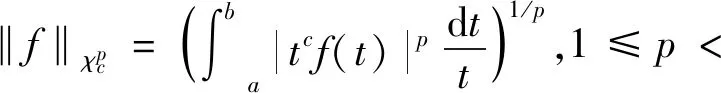
和

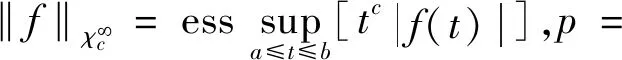
(5)

和

(6)

Katugampola分?jǐn)?shù)階積分也稱為ρ-Riemann-Liouville分?jǐn)?shù)階積分[4]，它推廣Riemann-Liouville分?jǐn)?shù)階積分和Hadamard分?jǐn)?shù)階積分[5-6]：

(7)

和

(8)

1.4 凸函數(shù)

定義3[7-8]設(shè)I為實(shí)數(shù)軸R上的任一區(qū)間，f(x)是區(qū)間I上的函數(shù)，如果對(duì)于?a,b∈I,a

f(λa+(1-λ)b)≤λf(a)+(1-λ)f(b).

(9)

則稱函數(shù)f(x)是區(qū)間I上的凸函數(shù).

設(shè)函數(shù)f(x)是區(qū)間I上的凸函數(shù)，a,b∈I,a

1.5 擬凸函數(shù)

定義4[9]設(shè)I為實(shí)數(shù)軸R上的任一區(qū)間，f(x)是區(qū)間I上的函數(shù)，如果對(duì)于?a,b∈I,a

f(λx+(1-λ)y)≤max{f(x),f(y)}.

(10)

則稱函數(shù)f(x)是區(qū)間I上的擬凸函數(shù).

顯然凸函數(shù)就是擬凸函數(shù)，但是擬凸函數(shù)不一定是凸函數(shù).

2 主要結(jié)論

首先，建立一個(gè)基于katugampola分?jǐn)?shù)階積分的等式.

(11)

其中函數(shù)f(xρ)在區(qū)間[a,b]上的Katugampola分?jǐn)?shù)階積分存在.

證明通過分部積分得到：

和

整理即得式(11)，引理1得證.

注1 在式(11)中當(dāng)ρ→1時(shí)取極限，即得到基于Riemann-Liouville分?jǐn)?shù)階積分的相關(guān)等式：

(12)

下面利用函數(shù)的擬凸性和引理1，基于Katugampola分?jǐn)?shù)階積分建立擬凸函數(shù)的Hermite-Hadamard型不等式.

定理1 設(shè)f:[aρ,bρ]→R是一個(gè)可微函數(shù)，其中ρ>0且0≤a

(13)

其中α>0且x∈[a,b].

證明利用引理1和|f′|的擬凸性，可以得到：

定理2 設(shè)f:[aρ,bρ]→R是一個(gè)可微函數(shù)，其中ρ>0且0≤a1)在區(qū)間(aρ,bρ)上是擬凸函數(shù)，那么有下面不等式成立：

(14)

其中α>0，0≤r≤q.

通過計(jì)算即得式(14)，定理2得證.

特別地，在定理2中分別取r=0 、r=1和r=q時(shí)，可以得到：

(15)

和

(16)

和

(17)

類似定理2的證明方法，還可以得到下述結(jié)論：

定理3 設(shè)f:[aρ,bρ]→R是一個(gè)可微函數(shù)，其中ρ>0且0≤a1)在區(qū)間(aρ,bρ)上是擬凸函數(shù)，則下面不等式成立：

(18)

其中α>0，0≤r≤min{q,q(ρ-1)}.

特別地，在定理3中分別取r=1和r=q時(shí)，可以得到：

(19)

和

(20)

定理4 設(shè)f:[aρ,bρ]→R是一個(gè)可微函數(shù)，其中ρ>0且0≤a1)在區(qū)間(aρ,bρ)上是可微的，則下面不等式成立：

(21)

其中α>0，0≤r≤min{q,qρα}.

特別地，在定理4中分別取r=1、r=q和r=qα?xí)r，可以得到：

(22)

和

(23)

和

(24)

注2 在式(13)～(24)中當(dāng)ρ→1時(shí)取極限，即得到基于Riemann-Liouville分?jǐn)?shù)階積分的相關(guān)結(jié)論.