基于觀測器的Markovian跳變廣義生物系統的滑模控制
王 靜,張 翼
(沈陽工業大學 理學院,沈陽 110870)
廣義系統也被稱為奇異系統,是一種數學表示形式,是描述和研究實際模型的有力工具,因此,廣義系統受到了越來越多學者的關注[1-3].而在系統參數擾動的情況下,廣義系統就不具有結構的穩定性,而Markovian跳變系統能有效地描述這類參數擾動下結構的突變,Markovian跳變是一類特殊的隨機系統,用來刻畫系統的結構和參數隨時間變化的系統[4-6].
近年來,將廣義系統的相關理論應用于生物系統已成為許多學者的研究重點,在實際系統中,種群會受到諸多隨機因素的影響,因此,研究隨機廣義生物系統的建模和穩定性分析具有重要的學術價值和實際意義[7-9].Zhang等[10]在廣義生物系統方向的研究做出了貢獻,并對種群在不同環境的影響下進行建模,以此來達到其環境的穩定性,在此之后很多學者對其進行深入研究,研究了污染環境中單一生物經濟系統的建模和控制,且提出了一種新的隨機平均方法來分析高斯白噪聲激勵下的沖擊振動系統[11].Lee K等[12]給出了具有Markovian跳變的廣義生物經濟系統的隨機最優保成本控制.總而言之,廣義系統在生物經濟領域的應用中有著廣闊的前景.
滑模控制(SMC)作為一種非線性控制策略,具有響應快、速度快等優點,SMC能夠克服系統的一些不確定性,對擾動和建模都具有較強的魯棒性[13],且在系統處于滑模相位時能夠完全補償匹配的不確定性[14-17].SMC目前已經應用到很多復雜系統中,如廣義系統、電力系統、生物系統等,并且SMC對各種復雜動力系統的相關介紹[18-19].概括來說,SMC就是通過設計SMC律,在有限的時間內將系統的軌跡驅動到預先設計的、具有穩定性等理想特性的滑動面中[20],給出了一種基于觀測器的線性積分滑模控制方法,并且最終保持穩定.
本文主要研究的是基于觀測器的Markovian的隨機廣義生物系統的變結構控制問題,將廣義生物系統理論與T-S模糊規則相結合,將生物種群的密度控制在一個有界的范圍內,并且消除系統中的一些不確定因素,建立T-S模糊模型,并提出了基于觀測器的有限時間的模糊滑模控制方法,設計了一種模糊滑模控制器,以保證在規定時間之前的有限時間內到達滑模面.并且保證了觀測器控制系統在到達階段和滑動運動階段同時具有有界性.
1 模型建立
由于種群在不同階段的生理機能有著差別,在不同程度上會影響種群的生存和滅絕,其階段結構的種群模型可表示為:
(1)
其中x1(t)表示幼年種群密度,x2(t)表示成年種群密度,a1表示幼年種群的出生率,b表示幼年種群轉化為成年種群轉化率與死亡率之和,δ表示幼年種群轉化為成年種群轉化率,β表示成年種群的內部競爭系數.
在模型(1)的基礎上,為了使具有階段結構的種群模型更具有實際意義,根據Gordon理論,建立廣義生物系統模型如下:
(2)
其中x3(t)表示整個養殖過程的成本,a2表示貸款用來購買幼年種群的比例,c1表示基本成本,E(t)表示對成年物種x2(t)的單位密度捕獲量,ρ表示捕獲單位成年種群的價格系數,c2表示貸款的系數,d1表示貸款利率,c3表示利潤里面用來償還貸款的部分,cE(t)代表總成本,m(t)表示經濟利潤.
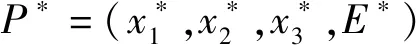
定理1 若系統(2)在正平衡點P*處是穩定的,則滿足以下不等式:
其中:
證明系統(2)的Jacobian矩陣可表示為:
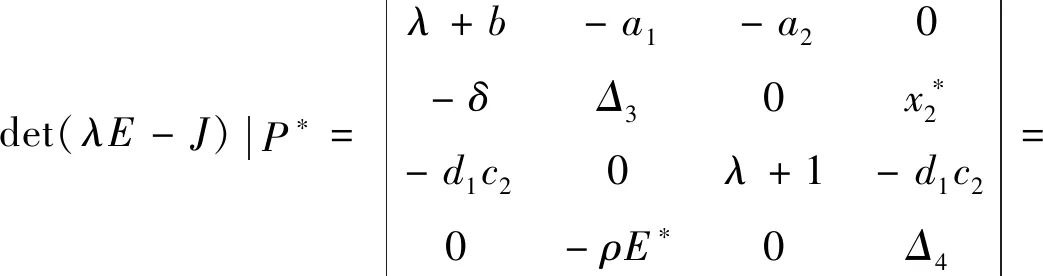
λ4+Λ1λ3+Λ2λ2+Λ3λ+Λ4=0

當滿足下列不等式時:
根據Routh-Hurwitz定理可知,系統(2)在平衡點P*處是穩定的.
在實際生活中,成熟種群的選擇并不是固定的,它受到多種因素的影響,如生產成本、利率、比較產量和匯率等.因此,假設成年種群的市場價格取有限集S={1,2,3,…,N}遵循Markovian跳變過程,且轉移概率矩陣為:Π?{λpq}.

則系統(2)可寫為:
(3)
當m(t)=0時,在正平衡點P*處做如下線性變換:
一般情況下,種群的出生率和幼年到成年的轉化率均會受外界環境和人類活動的影響,考慮到諸多因素的影響,在系統(3)上加入外部擾動和控制輸入,則有:
其中w(t)表示外部擾動,u(t)表示控制輸入,b11,b12,b13,b14表示外部擾動的系數,系統可以寫成:
其中:
令:
運用最大值最小值原理,z1(t),z2(t)可表示為:

其中Mi1+Mi2=1,i=1,2,Mij(i,j=1,2)為隸屬度函數,利用T-S模糊方法,將系統寫為:
上述廣義模糊控制系統包含4個模糊規則,若將模糊規則推廣到正整數r個控制系統,令p=rt,則有:
Ai(rt)=Ap,i,Bi(rt)=Bp,i,Jw,i(rt)=Jp,wi.
從而:
(4)
其中:
其中ωij(ζj(t))是ζj(t)在模糊集wij的隸屬度.
為了便于觀測器設計,在系統(4)中加入輸出向量:
(5)
其中y(t)∈Rp是控制輸出,Cp是具有適當維數的常數矩陣,當系統狀態不完全可訪問時,狀態反饋控制器可能失效.因此,給出如下滑模觀測器:
(6)
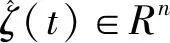
(7)
其中W(t)被作為擾動,且滿足:

(8)
定義1[21]若給定兩個標量c1>0和c2>0且c1 (9) 則系統(6)是關于{c1,c2,T,R,d}時域有界的. 定義2[22]考慮李雅普諾夫函數V(ζ(t),rt,t≥0),對ζ(t)進行兩次微分,則無窮小微分算子LV(t)可被定義為: (10) 引理1[23]給定任意向量ζ,y∈Rn×n和0 2ζTy≤ζTPζ+yTP-1y. (11) 在觀測器(6)的基礎上,給出模糊積分滑模面函數為: (12) 其中G∈Rm×n,且GBp,i是非奇異的,選取Kp,i∈Rm×n使得Ap,i+Bp,iKp,i是Hurwitz矩陣. 接下來,將設計一個基于觀測器的滑模控制器,使滑模面s(t)=0在給定時間T內可達,使得系統的狀態軌跡在有限時間內能夠驅動到滑模面上,且在隨后的時間保持在滑模面上. 定理2 給定觀測器系統(6)和滑模面函數(12),當滑模面s(t)=0在時間T*內可達,滑模控制律可表示為: (13) 證明選取Lyapunov函數: (14) 由式(6)和式(12)可知: 因此,可知式(14)的無窮小微分算子為: (15) (16) 因此,滑模面s(t)=0在時間T內可達. 將式(13)代入式(6)中,可得閉環系統為: (17) 定理3 若存在矩陣Pp>0,Q1>0和Q2>0,給定正常數μ>0,γ>0,和c′>0且滿足以下條件: Q1-12m2γI≥0, (18) Q2-3m2γI≥0, (19) (20) (21) 其中: 和 證明選擇Lyapunov函數: (22) 由定義2和文獻[24]中的無窮小微分算法可知: (23) 令PpLp,i=Hp,i,由式(20)可得到: LV(t)-αV(t)-βWT(t)WT(t)-γ(ρ(t)+δ)sgn(s(t))T(ρ(t)+δ)sgn(s(t))≤ ηT(t)Mp,iη(t)<0. (24) 由式(24)可知: e-αtε[LV(t)-αV(t)]≤e-αtε[βWT(t)WT(t)+γ(ρ(t)+δ)sgn(s(t))T(ρ(t)+δ)sgn(s(t))]. (25) 對式(25)從0到t進行積分有: (26) 由式(22)可知: (27) (28) 其中有: (29) 由式(27)~(29)可知: (30) ?t∈[0,T*],由式(21)可知: 基于滑模面(12)和觀測器(6),可知: (31) (32) 把式(32)代入式(6)中,可以得到滑動模態方程為: (33) 其中Ip=I-Bp,i(GBp,i)-1G. 定理4 若存在矩陣Pp>0,Hp,i>0和標量μ>0,γ>0,對于任意p∈S滿足以下條件: (34) (35) 其中λ1,λ2和c′在定理2中已經給出: 證明選取Lyapunov函數: (36) 其無窮小微分算子為: (37) (38) 由式(34)可知: LV(t)-αV(t)-βWT(t)WT(t)≤ηT(t)Mp,iη(t)<0. (39) 因此?t∈[0,T**],由式(35)可知: 從實際情況出發,由于物種受外界影響過多,深入物種對本土種群及人類帶來的影響,同時考慮經濟因素,利用模糊方法研究了具有Markovian跳變廣義生物系統的有限時間滑模控制問題,將廣義生物系統理論與T-S模糊規則相結合,并且消除系統中的一些不確定因素,建立T-S模糊模型,并設計滑模觀測器,在此基礎上,基于模糊觀測器構造積分滑動曲面. 其次,設計一種基于觀測器的滑模控制律,以保證給定滑模面在規定時間內有限時間可達.最后通過時域界性分析,分別在到達階段和滑動模態階段進行了有界性性能分析.這對于生態系統的持續良好循環,改善環境以及長期穩定地獲取經濟利益產生了積極而又深遠的影響.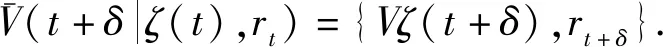
2 主要結果



3 時域有界性分析








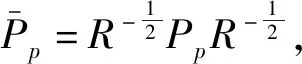
4 滑動模態的時域有界分析
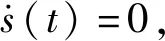


5 結論

