經典測量理論與項目反應理論的對比研究

胡恒瀟，董航遠

（西安思源學院教育學院，陜西 西安 710038）

1.引言

教育測量與評價是提升教育質量的有效手段。隨著社會對教育質量的關注度越來越高，教育質量的評價方法也變得多樣化。根據《國家中期教育改革和規劃綱要2010-2020年》，不僅要改善教育課程的質量，還要強調教育課程測量和評價的效果方法。學業成就測試是檢查教學質量的主要手段，不僅可以鞏固課堂所教授的內容，檢驗教學是否有效，促進教師改進教學方法，提升教學質量。同時，為以后考試題目的修改與篩選和試題庫的建立提供基礎。目前，教育測量理論中常用的理論有經典測量理論（Classical Test Theory）和項目反應理論（Item Response Theory）。

2.經典測量理論(Classical Test Theory,CTT)

經典測量理論(Classical Test Theory， CTT)始于19世紀末，于20世紀30年代形成較為完整的體系。由于其模型簡單，容易操作，至今為止在測量領域被廣泛應用。在經典測量理論中，觀察分數假設為真分數和誤差分數，其模型如下所示：

X=T+E

X：觀察分數

T：真分數

E：誤差

2.1 基本假設

第一，如果某被試者的分數是90分，與其說該分數是學生的真正能力，不如說是被觀察到的，即被測量的分數。該被測量的分數是指，未知的真正能力分數和測試過程中可能出現的誤差分數構成

第三，觀察分數是真分數和誤差分數之和。

2.2 難度(Item Difficulty)

難度是題目的難易程度，也稱難度系數（P），指在全體測試者中回答正確的測試者比率，即正確答案的概率。一般情況下，同樣的試題，大部分測試者都能答對，此試題的難度較小。難度系數越大，就意味試題越簡單。在計算試題的難度，應分為客觀題難度的計算和主觀題難度的計算。具體公式如下所示：

P：難度

N：總被試數

R：答對人數

在計算完每道題的難度后，可以通過對每部分題目的難度加權平均得出整套題的難度系數。確定了難度系數后，需要考慮測試的目的，如果是選拔性考試，難度系數值可較小，如果是學業測試，難度系數可較大。目前沒有絕對的難度評價標準，各學者都有提出各自的評價標準。本研究使用了Cangelosi（1990）提出的題目難度評價標準，難度系數為0.25以下，題目困難；0.25-0.75，難度適中；0.75以上，題目簡單。

2.3 區分度

區分度是指具體試題把不同水平的人區分開的程度，即題目的鑒別力。如，能力高的學生在各題中答對正確答案的比率要比能力低的學生答對正確答案的比率高。如果差異較少或沒有差異，那么這道題目的區分度較低或沒有區分度。區分度越高，越能區分出不同水平的學生，此題的價值也就越大。根據測驗及題目的計分方式不同，一般情況下可以用下列公式來求得：一是點雙列相關系數法，求考生總分與答對率之間的相關性。該方法適用于正確答案為1，錯誤答案為0，且考試總分為連續變量（如100分制的考試，89、91、98為連續變量）的情況。二是雙列相關系數法。雙列相關系數值反映了考生總分與答對率之間的相關性。雙柱相關系數比判別指數更準確，所以在大規模考試中，一般用它來表現試題的判別性。測量學家Ebel（1965）提出了題目難度評價標準，區分度值在0.4以上，區分度優良；0.3-0.39，區分度合格；0.2-0.29區分度較低，需修改；0.19以下，沒有區分度要淘汰。

3.項目反應理論（Item Response Theory,IRT）

項目反應理論，IRT)是教育測量領域的另一個代表性理論。它由瑟斯頓(1925)提出，由洛德和伯恩鮑姆發展而來，洛德和諾維克(1968)的經典教科書被認為是心理測量方法的里程碑。項目反應理論以數理統計理論為基礎，采用非線性概率形式構建反應的概率模型。在此前提下，根據不同能力水平考生可能和實際的正確答案，構建相應的數學模型，運用統計技術控制實驗誤差。從試題入手，將試題對測量的影響參數化，從而準確估計被試的能力。

3.1 基本假設

項目反應理論是建立在強假設的基礎之上。首先是能力單維性假設（unidimensionality）。所謂能力單維性假設是指，在測量試題時所有試題測量的必須是被試的同一種能力。同時需要滿足局部獨立性假設（local independence）。局部獨立性假設是指試題之間對被試的影響相互獨立互不干擾，被試之間的答對率也是相互獨立互不干擾。

3.2 項目特征曲線(Item Characteristic Curve: ICC)

項目特征曲線是用來衡量被試對某個項目能夠做出正確反應的概率的曲線。影響項目特征曲線的因素不僅包括項目的參數，還包括被試的潛在特征。項目特征曲線的X軸代表被試的能力水平，Y軸是答對答案的概率，被試的水平與題目本身擬合得較好的項目特征曲線的形狀為S型。

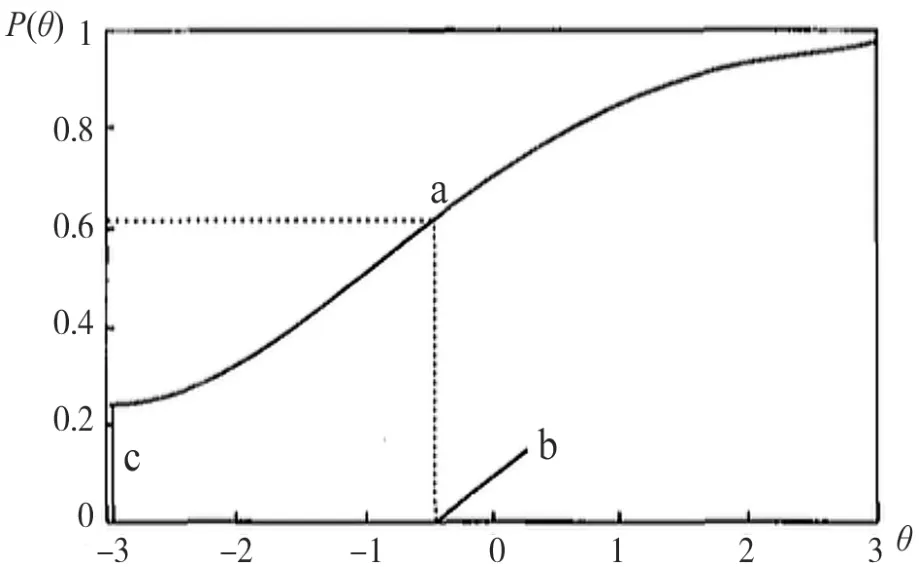
項目反應理論有多種數學最廣泛的一個模型，因參數的不同可以分為單參數Logistic模型（又稱Rasch模型）、雙參數Logistic模型和三參數Logistic模型。三參數Logistic模型主要由難度、區分度、猜測度構成其項模型，通常通過這些模型對項目的特征進行描述。Logistic是使用目特征曲線。如圖1所示：a：區分度；b：難度；c：猜測度；θ：能力。

3.3 難度、區分度、猜測度

區分度：如圖1所示，拐點處的斜率a，代表測驗項目的區分度，其值越大，說明區分度越高。韓國教授(2009)提出了題目區分度評價標準，在logistics模型中，區分度為0.00-0.34，無區分度；0.35-0.54，區分度低；0.65-1.34，區分度適中；1.35-1.69，區分度高；1.70以上，區分度非常高；+∞區分度完美。

難度：如圖1所示，拐點處所對應的θ(拐點在橫軸的投影)代表測驗項目的難度b，其值越大，說明難度越大。韓國教授(2009)提出了題目難度評價標準，難度系數在-0.2以下，非常簡單；-0.2--0.5，簡單；-0.5-0.5，難度適中；0.5-2.0，題目困難；2.0以上，題目非常困難。

猜測度：圖中特征曲線的截距c，表示項目的猜測指數。題目的推測指數是指，完全不具備能力的被試答對題目的概率。題目的推測指數越高，代表題目質量不佳，區分度越低。

4.經典測量理論與項目反應理論的對比

經典測量理論CTT 項目反應理論IRT模型 線性 非線性與樣本關系 項目參數依賴于樣本 項目參數獨立于樣本樣本大小 200-500 根據模型而變化，一般500以上能力指標 總分 能力參數測量精度 信度估計 能力參數難度 答對人數/總人數 項目特征曲線（ICC）中0.5對應的能力區分度 總分與項目分數的相關關系 項目特征曲線（ICC）中項目難度的斜率

經典測量理論和項目反應理論是教育測量理論中的兩個重要理論。經典測量理論的模型簡單，容易操作，對于小規模的測試，利用經典測量理論進行教育測量是十分實用的。作為一種傳統方法，它已經發展得比較完善，但仍有一些局限性：如采用的質量指標嚴重依賴樣本；信度估計精度不高；參數指標之間配套性較差。項目反應理論克服了經典測量理論在教育測量技術上的困境，將被試特質與其在項目上的反應聯系起來，具有項目參數獨立于樣本；被試與試題在同一量表之中；通過信息函數估計測量誤差等優勢，但由于測試條件要求嚴格，樣本數量過大，被試范圍要廣，操作復雜等局限，因此，兩種測量理論各有利弊，隨著教育測量理論的發展，這兩種理論也將不斷得到完善。在不同的評價目的、評價對象、評價條件下，選擇適當的教育測量理論，以獲得更加有效全面的信息，促進教育質量的提升。