GeoGebra軟件在中學數(shù)學函數(shù)教學中的應用

朱釗

[摘 ?要] 函數(shù)是貫穿中學數(shù)學知識的主線，函數(shù)的概念及其性質(zhì)是學生學習的重難點，且傳統(tǒng)教學較難突破. 文章例談了GeoGebra軟件在函數(shù)教學中的相關案例，包括函數(shù)的概念、單調(diào)性、奇偶性、各參數(shù)與函數(shù)圖像之間的關系，以及函數(shù)定點問題的相關案例，從數(shù)形結合的角度、以趣味的方式幫助學生發(fā)現(xiàn)并總結函數(shù)蘊藏的性質(zhì)及變化規(guī)律，改善學生函數(shù)的學習方式.

[關鍵詞] 信息技術;GeoGebra;中學函數(shù)教學

引言

信息技術與中學數(shù)學課程相結合是新課程標準的理念之一. GeoGebra作為一款自由且跨平臺的動態(tài)數(shù)學軟件，兼具“函數(shù)”“圖表”“集合”等功能，能夠同時處理代數(shù)與幾何，能夠動態(tài)化對象，功能強大，使用簡單，交互性強[1]. 函數(shù)是現(xiàn)代數(shù)學最基本的概念，是描述客觀世界中變量關系和規(guī)律的最為基本的數(shù)學語言和工具，是貫穿中學數(shù)學知識的主線，函數(shù)的相關概念及其圖像與性質(zhì)是學生學習的重難點. 對函數(shù)基本概念的不理解、對函數(shù)圖像的不明晰以及對函數(shù)模型的不敏感等是學生學習函數(shù)的慣性困境[2]，而傳統(tǒng)教學較難突破. 在此背景下，GeoGebra軟件的輔助教學可以使教學動態(tài)化、視覺化，從數(shù)形結合的角度、以趣味的方式幫助學生發(fā)現(xiàn)并總結函數(shù)蘊藏的性質(zhì)及變化規(guī)律，改善學生函數(shù)學習方式，大大提高了數(shù)學學習效率.

函數(shù)概念的課件案例

1. 教學分析

《普通高中數(shù)學課程標準（2017年版）》對于函數(shù)概念的教學要求在初中用變量之間的依賴關系描述函數(shù)的基礎上，用集合語言和對應關系刻畫函數(shù)，建立完整的函數(shù)概念，體會集合語言和對應關系在刻畫函數(shù)中的作用[3]. 高中數(shù)學中的函數(shù)基本概念比初中學過的函數(shù)概念更抽象、更精細、更準確. 建立一個數(shù)學概念的意義就是揭示它的本質(zhì)特征. 由于定義方式的高邏輯性與抽象性，學生難以理解對應關系的本質(zhì). 在傳統(tǒng)教學下，教師給出一個具體的函數(shù)表達式，學生可以理解每取一個x值都有唯一一個對應的y值，但這僅停留在代數(shù)階段，割裂了代數(shù)與幾何的結合. 若通過描點法畫圖，可以得出幾個點之間的對應關系，但這又無法將這幾個點一般化，學生無法深層次理解函數(shù)概念的本質(zhì). GeoGebra作為動態(tài)數(shù)學軟件恰好可以彌補這一不足，教師可以直接列舉學生熟悉的案例，應用GeoGebra軟件動態(tài)演示函數(shù)的定義域和值域，體現(xiàn)出任意一個x值都有唯一一個對應的y值，由此進行深層次探究.

2. 演示過程

首先在輸入框中輸入函數(shù)y=x3+2x2-5x+2，繪制該函數(shù)的圖像. 特別需要注意的是，在輸入過程中應將輸入法先切換為英文輸入法. 其次，制作該圖像的定義域與值域. 使用“對象上的點”這一功能在x軸上任取一點A，利用“平行線”功能過點A作關于y軸的平行線，與圖像的交點即為A在圖像上的對應點B，使用“垂線”功能過點B作y軸的垂線，與y軸的交點為C.

此時可以得到三個點，即點A，B，C. 我們發(fā)現(xiàn)點C即為點A在y軸上的對應點，一個x值對應一個y值，在傳統(tǒng)教學中通過畫圖也可以得到. 那么，如何讓學生理解兩個集合之間的對應關系呢？如何理解在自變量x變化過程中都有唯一一個y值與其對應呢？GeoGebra軟件在此案例中的“追蹤”功能可以彌補傳統(tǒng)教學中無法動態(tài)演示、無法讓學生幾何直觀的缺陷. 將點C右擊選擇“追蹤”功能，拖動控制它的點即自變量點A，或者建立滑動條，追蹤點C的運動軌跡. （見圖1）

在這一過程中，改變點A的位置即改變函數(shù)的定義域，定義域改變后則會跟蹤到點C的運動軌跡，即值域的變化情況. 那么，點A的值每改變一次，即會出現(xiàn)一個新的軌跡點. 通過繪制過程，我們可以明顯觀察到，在函數(shù)圖像上，每一個x值都有唯一一個與之對應的函數(shù)值y，從而深刻理解函數(shù)概念中集合之間的一一對應關系.

函數(shù)奇偶性的課件案例

1. 教學分析

函數(shù)的奇偶性是函數(shù)的基本性質(zhì)之一，刻畫的是函數(shù)圖像的對稱性. 一般地，如果對于函數(shù)y=f（x）的定義域D內(nèi)的任意實數(shù)x，都有f（-x）=f（x），那么就把函數(shù)y=f（x）叫作偶函數(shù)，而對于函數(shù)y=f（x）的定義域D內(nèi)的任意實數(shù)x，都有f（-x）= -f（x），那么就把函數(shù)y=f（x）叫作奇函數(shù). 在傳統(tǒng)教學下，關于奇偶性這一特性的引入是從數(shù)量關系來描述的，學生對于偶函數(shù)性質(zhì)的理解可以借助二次函數(shù)圖像. 對于奇函數(shù)，課本上給出了界定方式：f（-x）=-f（x），關于原點中心對稱. 傳統(tǒng)教學中的奇偶性教學無法體現(xiàn)自變量取值的任意性與動態(tài)性，要將學生的思維從靜態(tài)轉化為動態(tài)，可以利用GeoGebra繪制數(shù)值列表，觀察圖像上的點對應的橫坐標與縱坐標之間的關系，或將函數(shù)圖像關于原點旋轉180°，通過動態(tài)展示加深學生對奇偶性本質(zhì)的理解.

2. 演示過程

首先，繪制一個奇函數(shù)y=2x-2-x. 其次，為了體現(xiàn)f（-x）與f（x）的關系，需要在表格區(qū)繪制一個數(shù)值列表. 在Excel表格中從A1到A7分別輸入-3到3（間隔為1）的一列數(shù)據(jù)，在B2中輸入“f（A1）”，將表格下拉至“f（A7）”，可以自動得到相應的函數(shù)值，觀察自變量與函數(shù)值可以發(fā)現(xiàn)：f（-3）=-7.88=-f（3），f（2）=3.75= -f（-2）. 這是傳統(tǒng)教學中通過畫圖也可以得到的信息. 那么從動態(tài)的角度，可以用“對象上的點”在函數(shù)圖像上取一點A，使用“中心對稱”功能作出點A關于點O的中心對稱點A′，分別右擊A與A′將橫坐標與縱坐標記錄在表格區(qū);然后拖動點A，表格中將記錄兩點的運動軌跡，觀察對稱點的函數(shù)值之間的關系，可以發(fā)現(xiàn)：自變量相反，函數(shù)值也相反，即對于函數(shù)f（x）=2x-2-x定義域內(nèi)的任意實數(shù)x，都有f（-x）=-f（x），那么函數(shù)f（x）=2x-2-x就是奇函數(shù)（見圖2）. 這是從“數(shù)”的角度體現(xiàn)奇函數(shù)的代數(shù)性質(zhì).

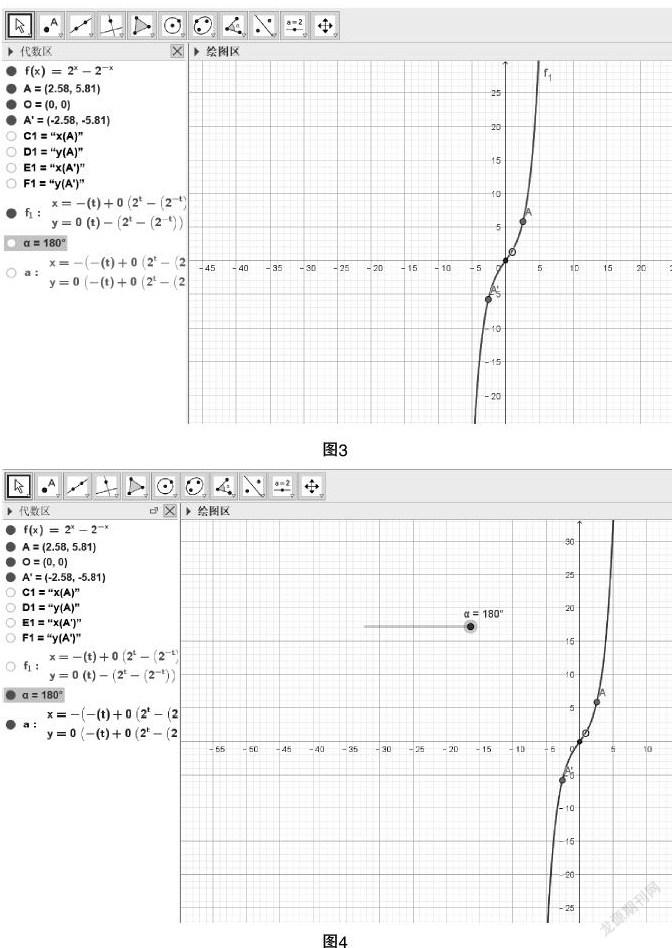
同樣，運用GeoGebra軟件還可以從“形”的角度體現(xiàn)奇函數(shù)的幾何性質(zhì)：選擇“旋轉”功能將整個函數(shù)圖像以原點為中心旋轉180°，旋轉之后與原圖像重合.（見圖3）

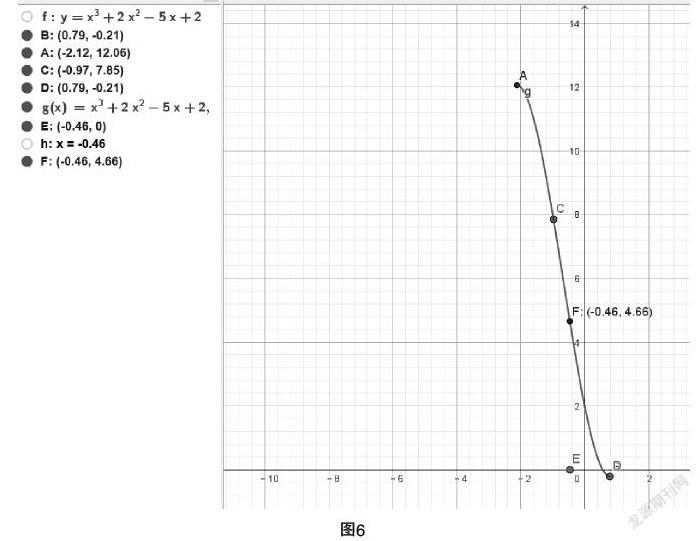
上述操作可以直接得出旋轉后的函數(shù)圖像，在教授過程中還可以向學生演示其旋轉的動態(tài)過程. 首先建立關于旋轉角度α的滑動條，設置旋轉區(qū)間，比如最小值0°，最大值180°. 選擇“旋轉”功能將整個函數(shù)圖像旋轉角度α，可以發(fā)現(xiàn)旋轉180°時與原圖像重合，得到奇函數(shù)關于原點中心對稱的性質(zhì). （見圖4）

GeoGebra軟件同樣可以用來驗證函數(shù)的奇偶性. 比如在輸入框內(nèi)輸入sinx，繪制該函數(shù)的圖像. 用同樣的方法，在輸入框內(nèi)輸入sin（-x）和-sinx. 可以在代數(shù)區(qū)看到三個函數(shù)的表達式，在繪圖區(qū)看到三個函數(shù)的圖像. 隱藏函數(shù)g（x）= -sinx的圖像，只顯示其余兩個函數(shù)的圖像，發(fā)現(xiàn)兩個圖像沒有重合，說明函數(shù)f（x）=sinx不是偶函數(shù);而隱藏函數(shù)f（x）=sinx的圖像，顯示另外兩個函數(shù)的圖像，發(fā)現(xiàn)圖像重合，說明函數(shù)f（x）=sinx是奇函數(shù). （見圖5）

函數(shù)單調(diào)性的課件案例

1. 教學分析

函數(shù)的單調(diào)性是函數(shù)的基本性質(zhì)之一，刻畫的是函數(shù)的變化趨勢. 一般地，當函數(shù)f（x）的自變量x在其定義區(qū)間內(nèi)增大（或減小）時，函數(shù)值f（x）也隨之增大（或減小）. 函數(shù)f（x）的這兩種性質(zhì)叫作函數(shù)的單調(diào)性. 學生認識函數(shù)的單調(diào)性是先從初中的形象描述階段逐漸過渡到高中的抽象概括階段，而在初中數(shù)學中，學生接觸的絕大部分都是靜態(tài)的數(shù)學對象，進入高中后要用靜態(tài)的數(shù)學符號刻畫動態(tài)的數(shù)學對象對學生來說是一個難點. 例如，在判斷函數(shù)f（x）=x2在[0，+∞）上的單調(diào)性時，學生最常見的錯誤就是在給定區(qū)間里取兩個數(shù)，比如1和2，因為12<22，所以判斷f（x）=x2在[0，+∞）上單調(diào)遞增. 因此在學習該性質(zhì)時，教師可以利用GeoGebra軟件演示函數(shù)的動態(tài)變化，將有限驗證擴大到動態(tài)下的無限，以數(shù)形結合幫助學生理解函數(shù)單調(diào)性的本質(zhì)，有效突破難點.

2. 演示過程

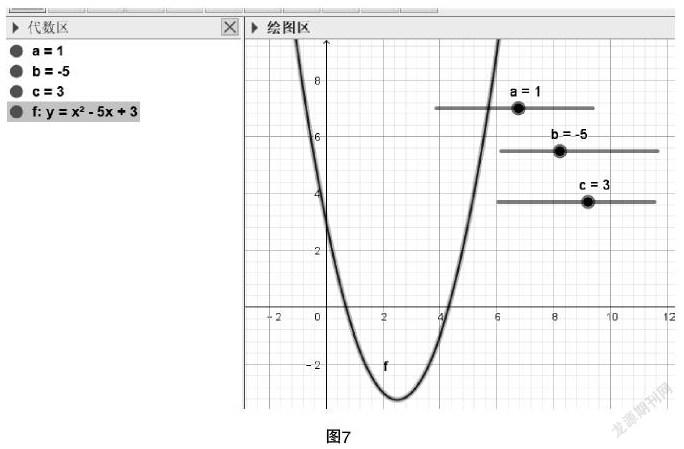
GeoGebra軟件可以用于函數(shù)單調(diào)性的導入部分. 例如，首先繪制出函數(shù)y=x3+2x2-5x+2的圖像，其次在圖像內(nèi)構造該函數(shù)的單調(diào)區(qū)間. 選擇“極值點”功能，點擊函數(shù)會自動出現(xiàn)兩個極值點A，B，在函數(shù)圖像上選取單調(diào)遞減區(qū)間. 對于此時的單調(diào)遞增區(qū)間，可以設置隱藏按鈕，研究起來會更加直觀清晰. 在遞減區(qū)間中任選一點E，構造點E在函數(shù)上的對應點F，選擇點E右擊“追加動畫”，選擇左下角的播放鍵讓播放暫停，可以觀察到動畫內(nèi)，當自變量x從點A的橫坐標-2.12移動至點D的橫坐標0.79時，x的值越大，所對應的函數(shù)值從12.06下降至-0.21，越來越小，即任意取-2.12≤x<x≤0.79，都有f（x）>f（x）. 在這個環(huán)節(jié)中，讓學生領悟到兩點：一是所取的自變量具有任意性;二是比較對應的函數(shù)值的大小. 同樣，在演示過程中，我們可以選擇“函數(shù)檢視”，通過列出各個點的坐標，也可以觀察到：當xy. 借助此演示，讓學生進一步歸納概括出函數(shù)單調(diào)性的文字語言表達及數(shù)學符號表達，深化學生對單調(diào)性的理解. （見圖6）

函數(shù)各參數(shù)與圖像之間的關系的課件案例

1. 教學分析

二次函數(shù)的各參數(shù)變化對函數(shù)圖像的影響是教學的難點. 在傳統(tǒng)教學中，大部分學生僅僅將函數(shù)看作是表達式，割裂了各參數(shù)與圖像之間的關系，難以從運動變化的角度理解其本質(zhì)特征. 而GeoGebra軟件可以動態(tài)演示出三個參數(shù)的變化所引起的函數(shù)圖像的變化，突破了傳統(tǒng)教學.

2. 演示過程

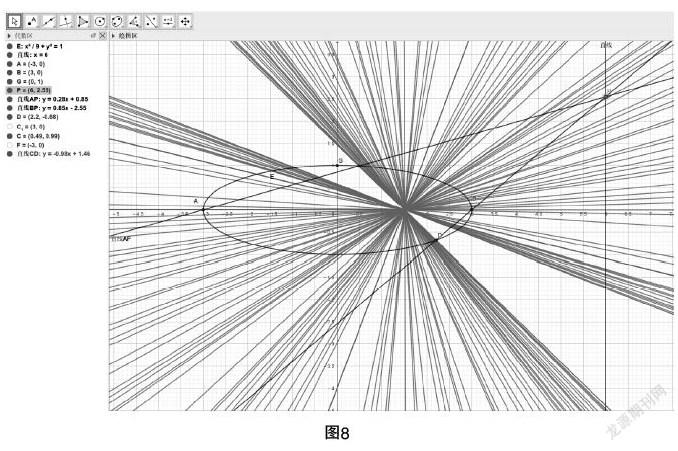
首先可以在自定義區(qū)間內(nèi)建立三個參數(shù)滑動條a，b，c，比如自定義區(qū)間是[-20，20]，在輸入框中輸入a=1，b=-5，c=3，然后在輸入框中輸入y=ax2+bx+c，繪圖區(qū)就會顯示出函數(shù)y=x2-5x+3的圖像. 教師可以多做幾次實驗，只拖動滑動條a時，觀察函數(shù)圖像的變化，可以發(fā)現(xiàn)參數(shù)a決定拋物線開口的方向和大小. 當a>0時，開口向上;當a<0時，開口向下. 當a越大時，拋物線的開口越小;反之，當a越小時，拋物線的開口越大. 當只拖動b的滑動條時，可以發(fā)現(xiàn)參數(shù)b改變的是函數(shù)圖像的對稱軸以及它的頂點. 當只拖動c的滑動條時，可以發(fā)現(xiàn)參數(shù)c決定了拋物線與y軸的交點位置. 當c>0時，函數(shù)與y軸交于正半軸;當c<0時，函數(shù)與y軸交于負半軸. 通過GeoGebra軟件的演示，可以使學生很快達成對以上規(guī)律的共識.

除此之外，我們還可以探究更多的數(shù)學奧秘. 比如各參數(shù)之間的關系，當a，b同號時，觀察可得二次函數(shù)的對稱軸在y軸左側;當a，b異號時，對稱軸在y軸右側;當b=0時，對稱軸就是y軸. 以及a，b，c共同決定判別式Δ=b2-4ac的符號，進而決定函數(shù)圖像與x軸的交點問題. 當Δ=0時，與x軸只有一個交點;當Δ>0時，與x軸有兩個交點;當Δ<0時，則沒有交點. 這可以轉化為一元二次方程根的情況、零點問題，讓學生深刻體會到函數(shù)是貫穿中學數(shù)學的主線，體會數(shù)形結合與分類討論思想. （見圖7）

同理，在GeoGebra軟件的使用下，學生也能快速領會A，ω，φ三個參數(shù)的變化對三角函數(shù)y=Asin（ωx+φ）圖像變化的影響. GeoGebra軟件建立了數(shù)與形之間的關系，有利于函數(shù)教學的整體把握，有利于函數(shù)知識結構的整體建立.

函數(shù)解題的課件案例

Geogebra軟件同樣可以用來進行解題驗證，諸如函數(shù)的定點問題、零點問題、軌跡問題等. 下面以2020年高考數(shù)學全國一卷中的一道定點問題為例：

已知A，B分別為橢圓E：+y2=1（a>1）的左、右頂點，G為E的上頂點，·=8，P為直線x=6上的動點，PA與E的另一交點為C，PB與E的另一交點為D. （1）求E的方程;（2）證明：直線CD過定點.

對于問題（1）的求解，通過已知可得A（-a，0），B（a，0），G（0，1），即可求得·=a2-1，結合已知可求得a2=9.

對于問題（2）的求解，考查的是計算能力與轉化思想、推理論證能力，屬于難題，可以使用Geogebra軟件得到或者驗證問題（2）的答案.

首先根據(jù)題意構建場景，切換英文半角符號，在輸入框內(nèi)直接輸入：橢圓+y2=1以及直線x=6，左、右頂點分別為A，B，上頂點為G. 使用“對象上的點”在直線x=6上任取一點P，連接直線AP與直線BP，與橢圓分別交于另一點C與另一點D，連接CD. 為顯示清晰，將直線CD用紅色標記，并右擊“開啟追蹤”. 拖動決定直線CD變化的起始點P，直線CD隨之運動并自動顯示出直線CD的運動軌跡，如圖8所示. 通過觀察圖像，可知直線CD恒過定點，0.

對于軌跡問題、定點問題等都可以通過GeoGebra軟件來驗證答案，同時可以根據(jù)答案幫助思考，產(chǎn)生思路. 但是需要注意的是，信息技術只是輔助教學的一種工具，在求解答案的過程中，還是需要認真思考并及時歸納總結.

總結

函數(shù)是現(xiàn)代數(shù)學最基本的概念，是描述客觀世界中變量關系和規(guī)律的最為基本的數(shù)學語言和工具，是貫穿中學數(shù)學知識的主線. 數(shù)形結合是函數(shù)學習的重要思想之一，傳統(tǒng)教學中的函數(shù)教學無法將數(shù)字動態(tài)化、可視化，GeoGebra軟件的輔助可以突破傳統(tǒng)教學中的不足，幫助學生深刻理解函數(shù)的變化規(guī)律及性質(zhì).

教師在運用GeoGebra的同時，可以教授學生使用方法，提高學生的主體意識，培養(yǎng)學生自主學習的能力. 特別需要注意的是，信息化設備只是用來輔助教學的一種手段，教師應加強自身的專業(yè)能力，處理好信息化與教學內(nèi)容之間的關系，拓展信息化與其他教學方面的聯(lián)系，發(fā)揮出信息化教學的最大優(yōu)勢.

參考文獻：

[1] ?http：//baike.baidu.com/item/geogebra.

[2] ?司業(yè)佳. Geogebra：輔助函數(shù)教學的利器[J]. 數(shù)學教學通訊，2018（24）.

[3] ?中華人民共和國教育部制定. 普通高中數(shù)學課程標準[M]. 北京：人民教育出版社，2017.

3181500316533