基于FPGA的NLFM信號參數化產生方法

楊 陽，沈 洋，王靜嬌，刁志龍

(中國船舶集團有限公司第八研究院，南京 211153)

0 引 言

由于線性調頻信號經脈沖壓縮后僅能獲得-13.2 dB的距離旁瓣，一般需要加窗函數來抑制旁瓣，從而導致脈壓后的信噪比降低、主瓣展寬。非線性調頻(NLFM)信號通過對功率譜進行加權修正避免了脈壓時加窗造成的信噪比損失，近年來獲得了大量運用[1]，多樣的設計優化方法也應運而生。

NLFM信號的產生比線性調頻復雜，且模板眾多，很難用單一的數學模型描述。雷達實時基帶波形產生常常采用基于FPGA的DDS技術，該方法不僅輸出信號形式多樣，且穩定性高[2]。對于少量的NLFM產生需求，一般采用查表法和CORDIC計算法：查表法將信號所有采樣點信息存于ROM中，同時也快速消耗存儲資源，難以存放大量NLFM信號；CORDIC計算法對NLFM信號特定的調頻函數或窗函數進行實時計算，定制性強，當引入新的信號模型時需要進行針對性開發，同樣難以適應參數化的批量產生需求。

本文以DDS技術為基礎，介紹了一種基于FPGA的NLFM信號參數化產生方法：從調頻函數曲線切入，提出了兩種曲線的線性擬合方法，并進行了逼近誤差比較；在此基礎上從工程實際出發，對基于正弦、正切模板的NLFM信號分別進行了脈壓效果評估。

1 NLFM信號線性逼近原理

在雷達系統中廣泛應用的NLFM波形包含基于正弦和基于正切的波形。對于基于正弦的波形，時間與頻率的關系為

(1)

式中，T為脈沖寬度；B為信號帶寬；k為副瓣電平控制因子。

對于基于正切的波形，時間與頻率的關系為

f=Btan(2βt/T)/(2tanβ),-T/2≤t≤T/2

(2)

式中，β=tan-1α,0≤α≤∞，α為時間副瓣電平控制因子[3]。

基于兩類模板的NLFM信號調頻函數如圖1所示。可以看出，有固定模板的調頻曲線硬件已難以直接實現，對于更為復雜的超越函數只能采用近似方法實時產生。

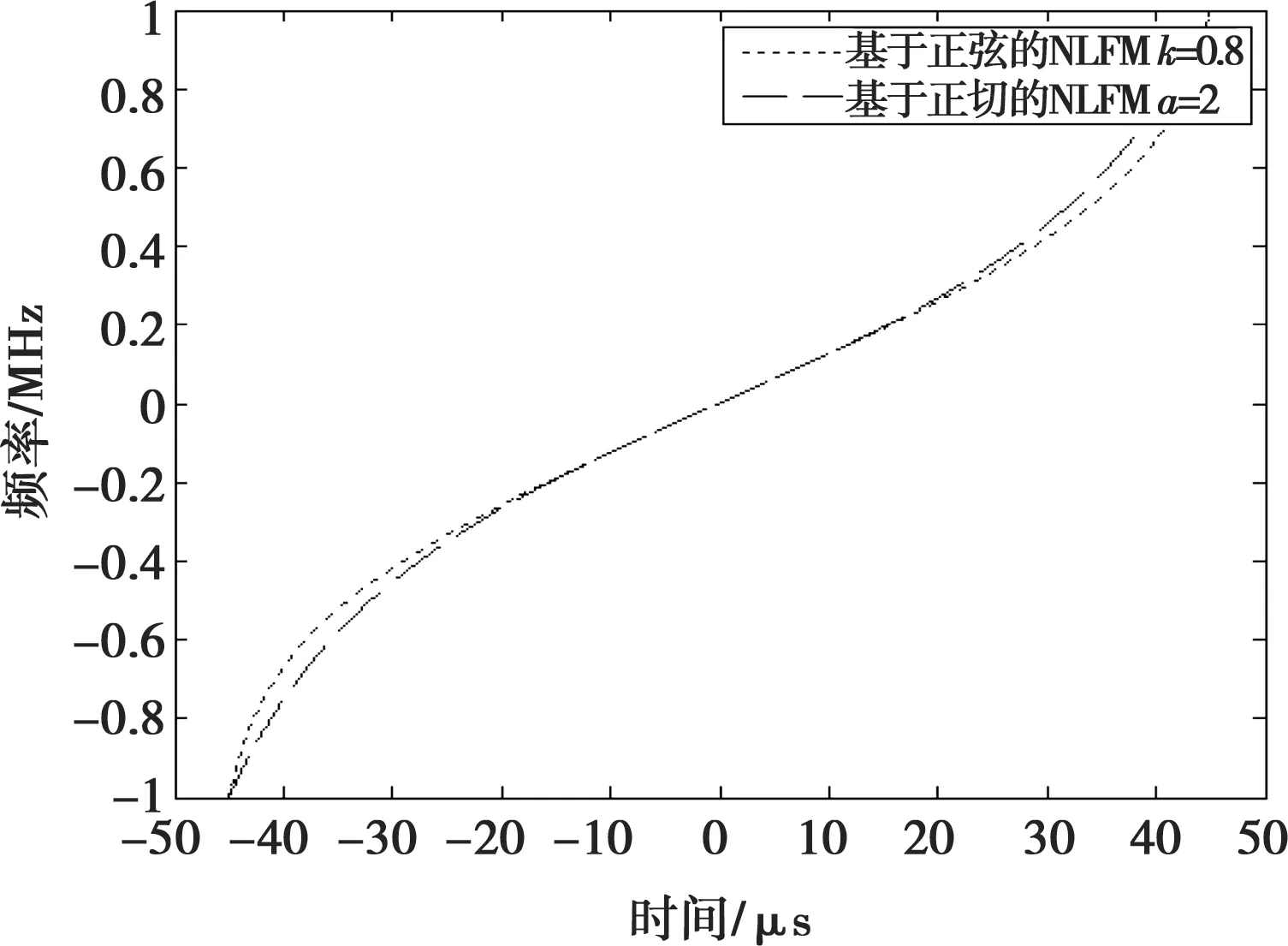
圖1 NLFM信號的調頻函數

目前在FPGA中，計算超越函數一般采用查表法、級數展開法、CORDIC法和分段線性逼近法等[4-5]：查表法將波形或調頻的所有采樣點信息存于本地查找表中，結構簡單，易于實現，但對存儲資源消耗極大；級數展開法將超越函數近似展開為多階泰勒級數，實現較復雜，對DSP資源提出了很高的要求；CORDIC法通過多次迭代能夠獲得很高的計算精度，且僅涉及簡單的移位、加減運算，非常適合FPGA使用，但針對不同NLFM模板必須進行定制化開發，難以適應參數化批量產生需求；分段線性逼近融合了查表法和一階多項式，實現過程更接近LFM信號，是計算超越函數的理想選擇。分段數越多，消耗的查找表資源越多，但近似的精度越高，因此該方法的核心問題是分段算法。相比于如文獻[6]提出的通過調節分段數來獲得確定的計算精度，批量的NLFM實時產生更希望以確定的分段數獲得滿足脈壓需求的計算精度。

1.1 分段線性逼近算法原理

線性逼近算法的原理是按照一定準則，將函數f(x)劃分為若干區間，每個區間內用一條線段近似逼近f(x)曲線，原理如圖2所示。

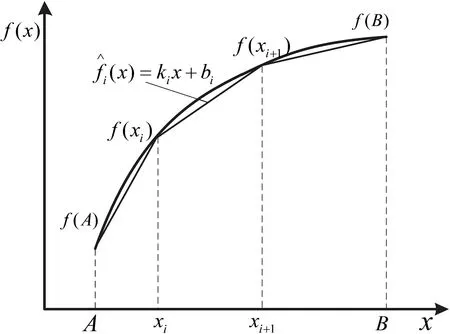
圖2 分段線性逼近原理

不論是OED_PWL法[6]還是2k等分法[7]，本質上都是在x軸上將f(x)等分為若干區間，即xi+1-xi=l，l為常數。這些方法原理簡單，但存在兩個問題：一是當函數非單調時，在某些單調特性變化的區間，其近似誤差會大大增加，如圖3所示；二是這些方法未考慮函數本身性質，對于快速變化的區間，其近似精度不高。

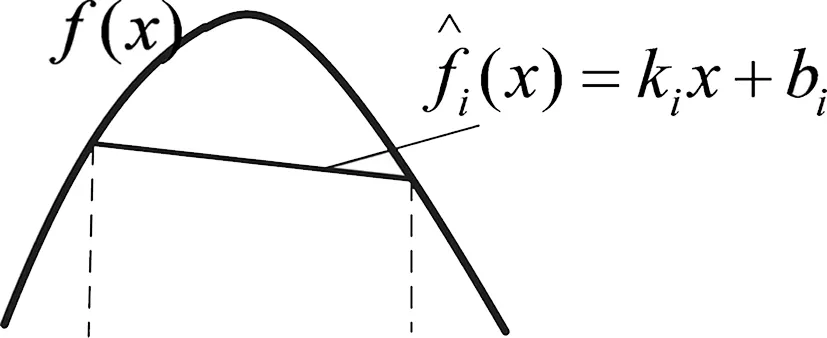
圖3 非單調區間誤差示意

1.2 改進的分段線性逼近

針對上述問題，本文提出兩種改進算法，以期在確定的分段數下獲得更高的近似精度。

(1)在區間等分法基礎上，通過對函數的單調區間進行劃分，避免在特定單調性變化的區間出現近似精度大幅下降的情況，可稱為單調法，具體算法流程如圖4所示。

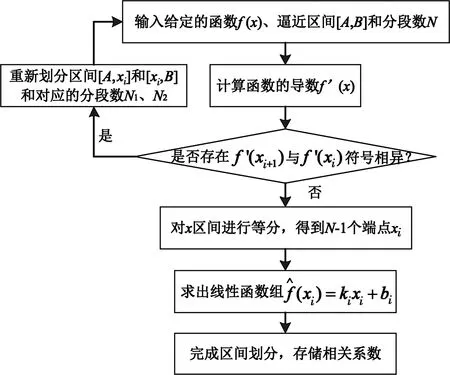
圖4 單調區間分段逼近流程

值得注意的是，由于NLFM信號本身在頻率和相位上是連續的，實際應用時可不存儲系數bi，以進一步壓縮存儲空間。

(2)從線性逼近的原理切入，一段曲線偏離直線的程度越大，用直線逼近曲線產生的誤差就越大，就需要采用更多的分段進行逼近。曲率是針對曲線上某個點的切線方向角對弧長的轉動率，代表了曲線偏離直線的程度。曲率K(其倒數為曲率半徑ρ)的計算公式如下：

(3)

圖5說明了該方法的分段流程：首先對輸入函數進行凹凸性判斷，當曲線凹凸性不一致時，則對其進行重新分段，直到區間內凹凸性完全一致；然后求取函數曲率，并對其進行積分；對曲率積分進行等區間分段，確定分段端點；最后完成區間劃分和參數求取。該算法對曲率積分等分，可稱為曲率法。

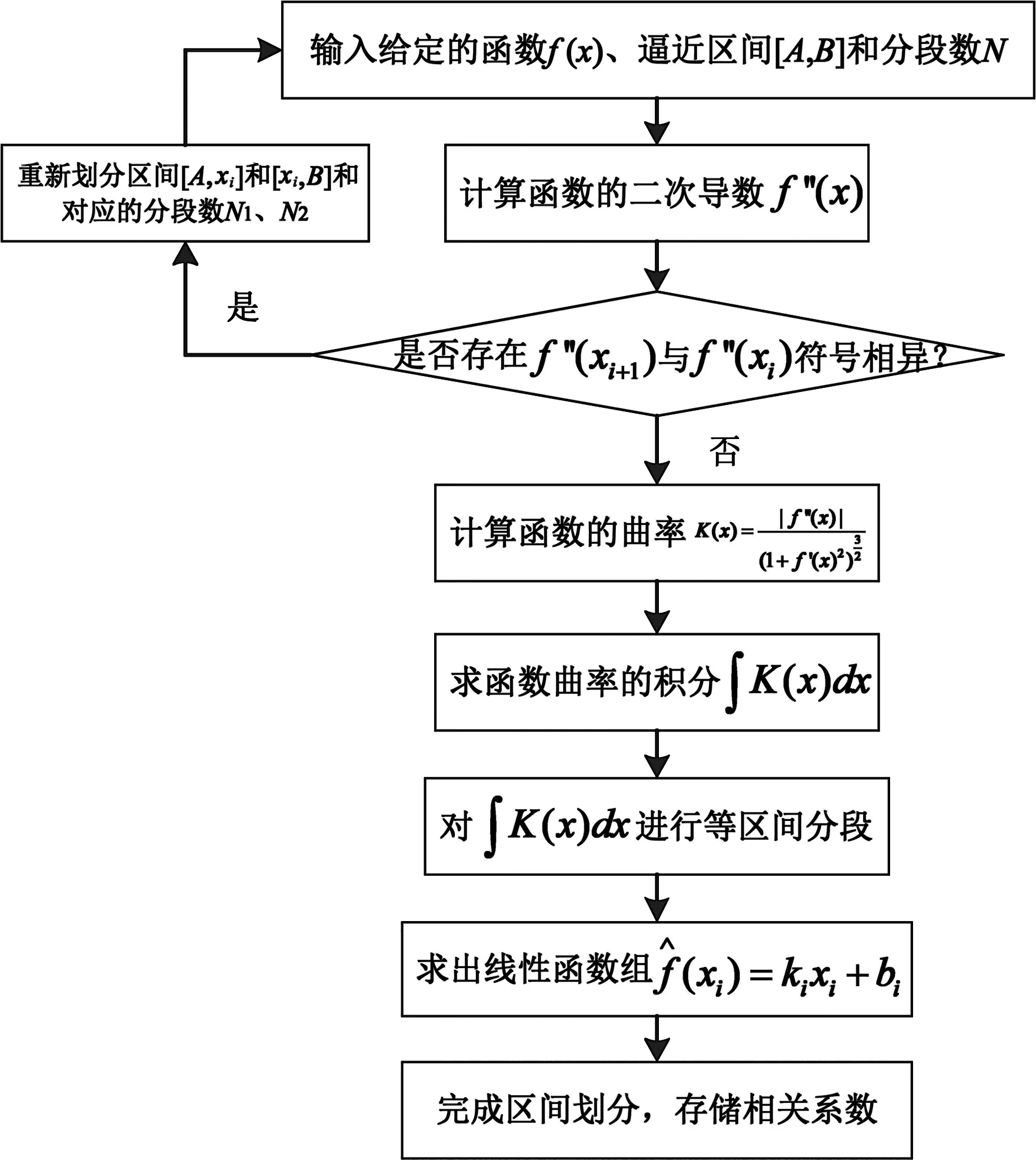
圖5 曲率法分段逼近流程

1.3 算法性能驗證

仍然以上述分別基于正弦和正切模板的NLFM信號為驗證對象，測試兩類算法與理想曲線的均方根誤差，誤差單位為kHz，其中信號帶寬B為2 MHz，脈寬T為90 μs，正弦和正切波形的副瓣電平控制因子分別為k=0.8和α=2。

表1和表2分別給出了單調法和曲率法的誤差統計結果。可以看出，由于正弦較正切模板的NLFM信號調頻函數曲率大，曲率法相對單調法在正弦NLFM信號的逼近上有較為明顯的優勢。當分段數為21時，其逼近誤差比單調法小25%；隨著分段數增加，兩者差距減小；當分段數為41時，兩類算法性能基本相當。對于正切NLFM信號，由于調頻函數本身曲率較小，兩類算法的差異并不明顯。

表1 單調法均方根誤差(RMSE)

表2 曲率法均方根誤差(RMSE)

2 FPGA實現過程

2.1 實現方法

完成逼近算法設計后，本文采用Matlab和Vivado開發套件，在XilinxVirtex-7 FPGA上實現了所述算法的NLFM信號實時產生。Matlab對輸入調頻函數依照算法分段，并給出每個子區間的線性函數參數，形成.coe文件存儲于FPGA本地ROM中。FPGA在時序上依次讀取分段信息，完成NLFM產生。FPGA實現流程如圖6所示。

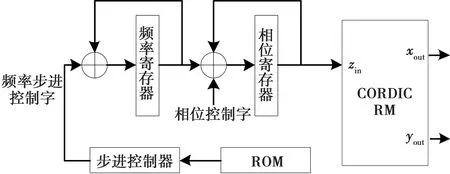
圖6 NLFM信號FPGA實現流程

該流程在LFM實現流程的基礎上增加了步進控制器和ROM表，步進控制器從ROM中讀取各子區間的參數信息，包括區間長度和斜率，并隨時間實時調整頻率步進控制字；最終相位信息輸入CORDIC，經簡單的旋轉后形成波形IQ信號輸出。

2.2 脈壓性能仿真

脈壓性能是雷達探測波形的一個核心指標。下面采用線性逼近法產生的NLFM波形進行脈壓，對逼近算法性能進行評估。其中，帶寬B為2 MHz，脈寬T為90 μs，采樣率fs為100 MHz，分段數N=31，正弦和正切波形的副瓣電平控制因子分別為k=0.8和α=2。兩種方法對正弦、正切NLFM的逼近結果分別如圖7～10所示。

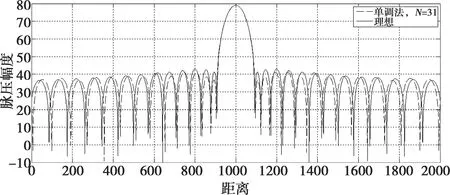
圖7 單調法逼近正弦NLFM波形脈壓

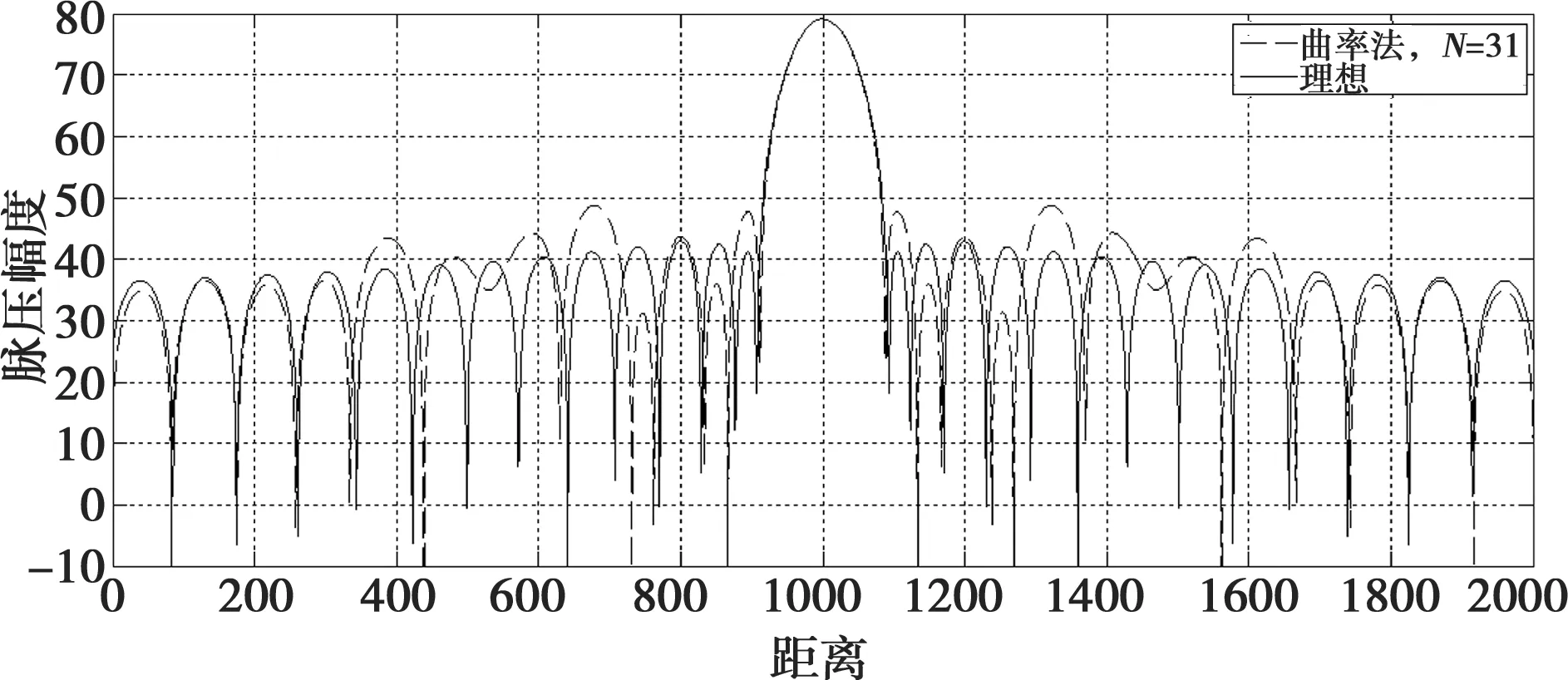
圖8 曲率法逼近正弦NLFM波形脈壓

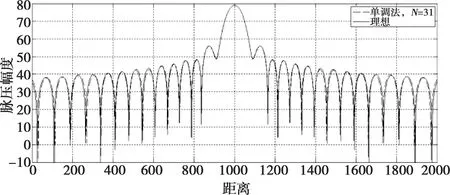
圖9 單調法逼近正切NLFM波形脈壓

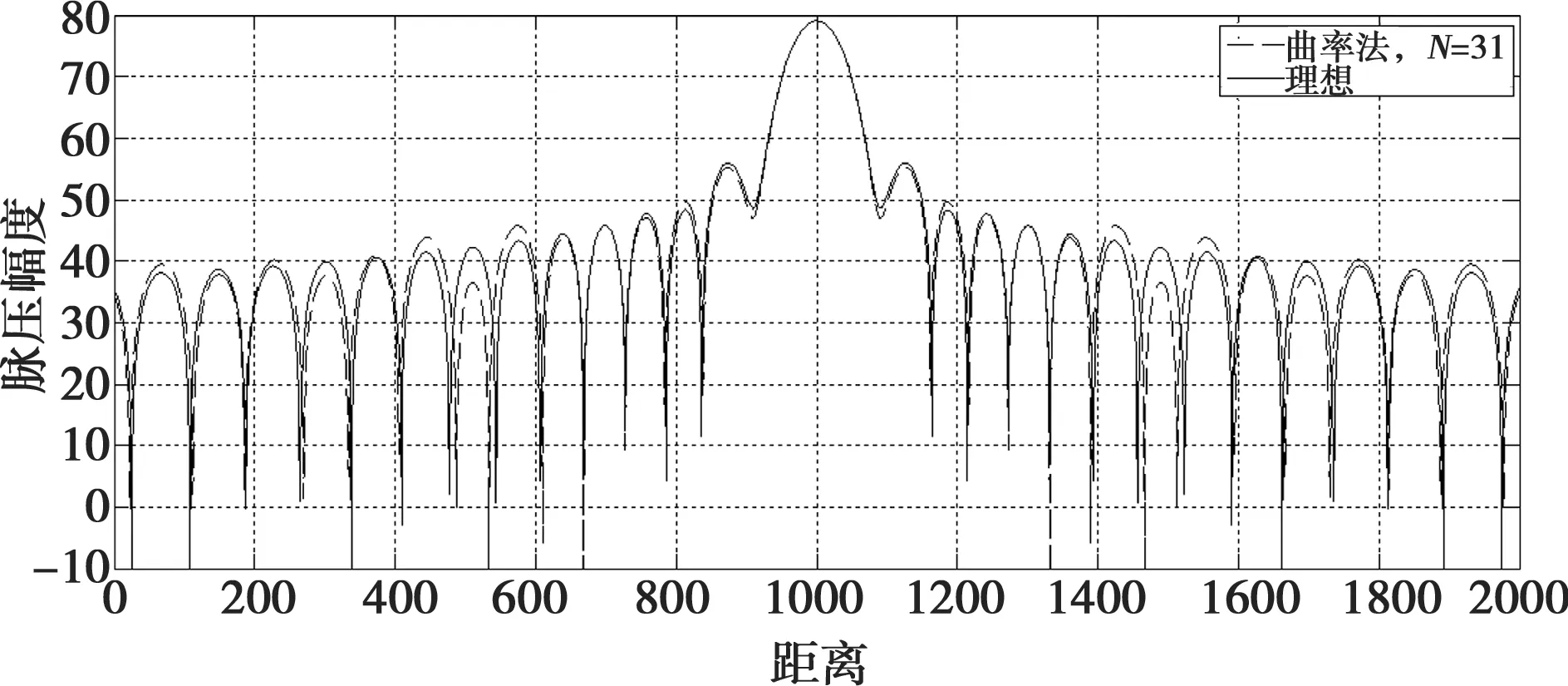
圖10 曲率法逼近正切NLFM波形脈壓

當分段數N=31時，不論基于正弦或正切，采用單調法逼近的NLFM信號均表現出良好的脈壓特性，與理想脈壓結果幾乎完全一致；而采用曲率法逼近的正弦波形脈壓結果則在旁瓣產生了明顯的抬高，這是由于設計NLFM波形的窗函數在頻帶邊緣快速變化，使得邊緣頻帶在脈壓中權重較小；而曲率法則傾向在快速變化的頻段做密集的分段逼近，造成權重較高但變化緩慢的頻段逼近誤差較大。因此，調頻函數的逼近誤差并不能完全反映分段逼近算法優劣，仍需以脈壓性能為最終考量。

3 結束語

本文介紹了NLFM波形逼近原理，并提出了基于等分法的兩種改良算法，計算了兩種算法的逼近誤差；同時闡述了基于FPGA的實時參數化產生流程，并以脈壓效果為標準對算法進行了評估。結果表明：雖然曲率法在逼近誤差方面性能優于單調法，但在脈壓時曲率法會產生一定程度的旁瓣畸變；而單調法逼近的脈壓結果與理想結果幾乎一致，能夠應用于工程。